Speed of sound

Most ultrasound applications involve transmitting short bursts, or pulses, of sound (typically two or three cycles long) into the body and receiving echoes from tissue interfaces. The time between transmitting a pulse and receiving an echo is used to determine the depth of the interface. The speed of sound in tissue must be known in order to calculate this depth.

The velocity of sound waves mostly depends on the properties of the transmitting medium and not significantly on the frequency or the wave amplitude (strength). As a general rule, gases, including air, exhibit the lowest propagation velocities, liquids have an intermediate range of velocities, and solids have the highest sound transmission velocities. For soft tissues, the average speed of sound is 1.54 mm/µs (1540 m/s). Variations exist in the speed of sound from one tissue to another, but, as Table 2.1 indicates, the speed of sound in various soft tissues deviates only slightly from the assumed average. On average, the speed of sound transmission in fat is lower than that in muscle.

Frequency and wavelength

The number of oscillations (cycles) per second of the vibrating elements in the transducer is the frequency of the sound wave. Frequency is expressed in cycles per second, or hertz (Hz). Audible sounds are in the range of 20 Hz to 20 kHz. Ultrasound refers to sound whose frequency is above the audible range (the prefix ultra means “beyond”). Diagnostic ultrasound applications use frequencies in the 2 to 15 MHz ( mega hertz, i.e., 2 million to 15 million Hz) frequency range. Because higher frequencies are associated with improved spatial detail (i.e., better detail resolution), sonographers use the highest frequency that still allows adequate depth to visualize tissue in a given scanning situation. Some applications that require very little penetration use frequencies as high as 50 MHz.

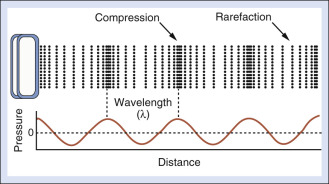
Fig. 2.1 shows a sound wave frozen in time. It illustrates accompanying compressions and rarefactions (expansions) in the medium that result from the pressure and particle oscillations. The wavelength λ is the spatial length of a cycle. It is described by the equation:

Sound waves produced by an ultrasound transducer. Vibrations of the transducer are coupled into the medium, producing local fluctuations in pressure. The fluctuations propagate through the medium in waves. The pressure amplitude is the maximum pressure variation, positive or negative. The diagram schematically illustrates compressions and rarefactions at an instant of time. The symbol λ is the acoustic wavelength.

Wavelength has relevance when describing dimensions of anatomic structures. The size of an object is more easily understood if given relative to the ultrasonic wavelength for the frequency of the sound beam. Similarly, the width of the ultrasound beam from a transducer depends in part on the wavelength. Higher frequency beams have shorter wavelengths and can be focused more tightly than lower frequency beams.

Amplitude, intensity, and power

A sound wave is a propagating pressure variation. The pressure profile that occurs for the wave in Fig. 2.1 appears in the lower part of the figure. The pressure amplitude is the maximal increase (or decrease) in the pressure, relevant to normal pressure, caused by the sound wave. The unit for pressure is the pascal (Pa). Ultrasound instruments can produce peak pressure amplitudes of millions of pascals in water when power controls on the instrument are set at maximum. As a benchmark for comparison, atmospheric pressure is approximately 0.1 MPa, so it is clear that ultrasound beams from medical devices significantly exceed this value. The high-pressure amplitudes of ultrasound pulses can burst contrast agent bubbles (see later and Chapter 35 ) that are sometimes injected into the bloodstream to enhance echo signals. Diagnostic levels, however, are not believed to create biologic effects in tissues if such gas bodies are not present.

The intensity (I) of a sound wave at a point in the medium is estimated by squaring the pressure amplitude (P) and using I = P ² /(2 ρc ), where ρ is the density of the medium and c is the speed of sound in it. Units for ultrasound intensity are watts per meter squared (W/m ² ) or multiples thereof, such as mW/cm ² . In water, a 2 MPa amplitude during the pulse corresponds to a pulse average intensity of 133 W/cm ² ! This is a high intensity, but, fortunately, it is not sustained by a diagnostic ultrasound device because the duty factor (i.e., the fraction of time the transducer actually emits ultrasound) is a few percent at most. Therefore the time-averaged acoustic intensity from an ultrasound instrument, found by averaging over a time that includes transmit pulses as well as the time between pulses, is much lower than the intensity during the pulse. Typical time-averaged intensities at the location in the ultrasound beam where the maximal values are found are in the order of 10 to 20 mW/cm ² for anatomic imaging. Doppler and color Doppler imaging modes have higher duty factors. Moreover, these modes tend to concentrate the acoustic energy into smaller areas. Output data for sonographic instruments are published and must be compliant with predefined limits.

The acoustic power produced by an instrument is the rate at which energy is emitted by the transducer. Average acoustic power levels in diagnostic ultrasonography are low because of the small duty factors used in most equipment. Typical power levels of 10 to 20 mW for B-mode imaging can triple or quadruple for Doppler modes of operation.

Acoustic output indicators

The transmit level, or the output power, on most instruments may be adjusted by the operator. Increasing the power applies a more energetic signal to the transducer, thereby increasing the pressure amplitude and increasing the power and the intensity of the waves produced. Higher power levels are advantageous because they enable detection of echoes from more weakly reflecting or deeper structures in the body. The disadvantage of high power levels is that they expose the tissue to greater amounts of acoustic energy, increasing the potential for biologic effects. Although there are no confirmed effects of ultrasound on patients during diagnostic ultrasound exposures, operators are encouraged to follow the ALARA (As Low As Reasonably Achievable) principle when adjusting the power level and other instrument controls that affect output levels (i.e., limit the output to that necessary to gather the diagnostic information needed).

To assist the implementation of the ALARA principle, output indicators are provided that are related to the biologic effects of ultrasound. One of the potential effects is cavitation, which refers to the activity of small gas bodies (bubbles) under the action of an ultrasound beam. When bubbles are present, such as when there are contrast agents in the ultrasound field, cavitation increases the local stresses on tissue that are associated with the ultrasound waves. If the wave amplitude is high enough, collapse of the gas body occurs, and this is accompanied by localized energy depositions (shock waves) that significantly exceed depositions that might occur without cavitation. Cavitation is related to the peak negative pressure in the ultrasound wave. The mechanical index (MI) describes this relationship. The current maximum MI in the field can be found on the display of most sonographic instruments ( Fig. 2.2 ).

Ultrasound image showing display of the mechanical index and thermal index. CCA , Common carotid artery; ED , end-diastolic; PS , peak-systolic.

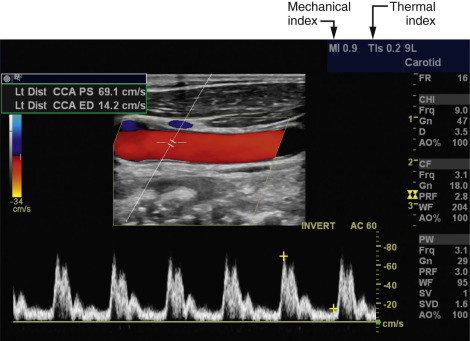
Ultrasound energy may also affect tissue by heating through absorption of the waves. Absorption is one of the mechanisms that result in attenuation of a sound beam as it propagates through tissue. A corresponding index, the thermal index (TI), is displayed to indicate the estimated temperature rise in the tissue (see Fig. 2.2 ). This is calculated with the time-averaged acoustic power or the time-averaged intensity, along with detailed mathematical models for the sound beam pattern and assumptions on the ultrasonic and thermal properties of the tissue. Depending on the application, an instrument will exhibit either a soft tissue thermal index value (TI _s ) or a thermal index for the case in which absorbing bone is at the beam focus (TI _b ). TI _c is a thermal index used for transcranial Doppler studies. The latter two indices are relevant because the temperature increase in bone during ultrasound imaging is greater than in soft tissues under the same acoustic conditions.

The acoustic output labeling standard calls for a clear display of MI and TI. The standard provides ultrasound system operators values of acoustic output quantities that are relevant to the possibility of biologic effects (risk) from the ultrasound exposures.

Risk and safety

In an ultrasound examination, acoustic energy is transmitted into the tissue. The possibility that the energy could produce a detrimental biologic effect, constituting risk, has been studied extensively by bioacoustics researchers and continues over decades. The American Institute of Ultrasound in Medicine (AIUM) official statement on the clinical safety of diagnostic ultrasound instrumentation (2012) follows:

Diagnostic ultrasound has been in use since the late 1950s. Given its known benefits and recognized efficacy for medical diagnosis, including use during human pregnancy, the American Institute of Ultrasound in Medicine herein addresses the clinical safety of such use: No independently confirmed adverse effects caused by exposure from present diagnostic ultrasound instruments have been reported in human patients in the absence of contrast agents. Biological effects (such as localized pulmonary bleeding) have been reported in mammalian systems at diagnostically relevant exposures but the clinical significance of such effects is not yet known. Ultrasound should be used by qualified health professionals to provide medical benefit to the patient. Ultrasound exposures during examinations should be as low as reasonably achievable (ALARA).

The responsibility for safety of medical diagnostic ultrasound equipment falls on everyone involved in manufacturing, regulating, and using this equipment. The acoustic output labeling standard requires manufacturers to provide the output indicators on their instruments to inform users of levels as they relate to potential biologic effects. These quantities enable users to implement the ALARA principle.

Decibel notation

Decibels (dB) are sometimes used to indicate relative power, intensity, and amplitude levels. Decibel levels express a ratio of acoustic power, intensity, or amplitude. Suppose one wishes to express how much greater (or smaller) one intensity ( I ₁ ) is relative to another ( I ₂ ). Their relative value in decibels is given by:

Thus the decibel relation between two intensities is the logarithm to the base 10 of their ratio multiplied by 10. The same equation holds for expressing the ratio of two power levels. The difference in decibels between two powers is found by taking the log ₁₀ of their ratio and multiplying by 10. Sometimes amplitudes rather than the intensities of two signals are used to express decibels. For a given decibel level, the intensity is proportional to the amplitude squared. Substituting the corresponding amplitudes ( A ₁ and A ₂ ) into Eq. 2.2 , squaring them, and taking into account that log ( x ² ) is 2(log x ), we have the relationship:

Decibels are used to describe the loudness of audible sounds. Here, the level of one sound is often expressed with no explicit comparison to another, such as “the sound intensity of the jet at takeoff was 110 dB.” However, with airborne sounds, a reference intensity is implied when not stated explicitly. This reference is I ₂ = 10 ⁻¹² W/m ² , the accepted threshold for human hearing.

Attenuation

As a sound beam propagates through tissue, its intensity decreases with increasing distance. This decrease with path length is called attenuation. Attenuation of medical ultrasound beams is caused primarily by absorption and additionally by reflection and scatter of the waves at boundaries between media having different densities or speeds of sound (i.e., echo generation).

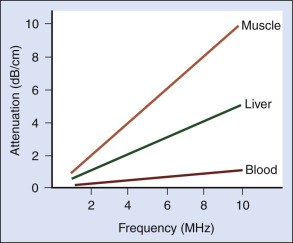
The rate of attenuation per unit distance is called the attenuation coefficient , expressed in decibels per centimeter. The attenuation coefficient depends on both the medium and the ultrasound frequency. Fig. 2.3 illustrates attenuation coefficients for three tissues, plotted versus the frequency. Attenuation is quite high for muscle and skin, has an intermediate value for large organs such as the liver, and is very low for fluids. For the liver, it is approximately 0.5 dB/cm at 1 MHz, whereas for blood, it is about 0.17 dB/cm at 1 MHz. An important characteristic of attenuation is its frequency dependence. For most soft tissues, the attenuation coefficient is nearly proportional to the frequency. The attenuation expressed in decibels would roughly double if the frequency were doubled. Thus higher-frequency ultrasound is attenuated more than lower frequency so that the high-frequency beams cannot penetrate as deeply as low-frequency beams. Diagnostic studies with higher frequency sound beams (7 MHz and above) are usually limited to superficial regions of the body. Lower frequencies (5 MHz and below) are used for imaging larger or deeper organs.

Variation of attenuation with tissue type and frequency.

Reflection

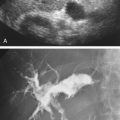
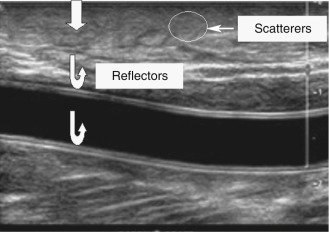
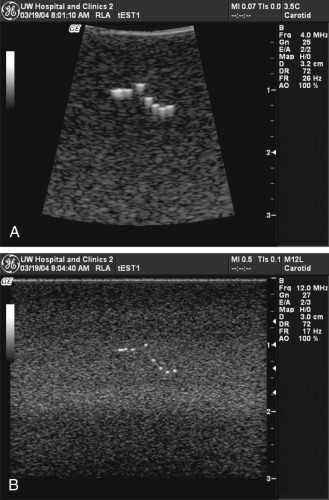
Fig. 2.4 shows an ultrasound image of the carotid artery in a healthy adult. The walls of the vessel can be seen because of reflection of sound waves. Echoes from muscle and other tissues are also produced by reflections and by ultrasonic scatter. Both reflection and scatter contribute to the detail seen on clinical ultrasound scans.

Gray-scale image of an arterial graft. Such images are constructed from echoes detected from large interfaces ( arrows ) and from small scatterers ( smooth echo region ). Bright dots on ultrasound gray-scale images indicate high-amplitude echoes, and dim dots indicate low amplitudes. Notice how the echoes from the vessel wall vary as the orientation changes slightly, characteristic of a specular reflector. The highest-amplitude echoes occur when the interface is perpendicular to the ultrasound beam. The interior of the vessel appears anechoic because blood has a lower backscatter level (lower echogenicity) than surrounding tissues. Scattering from small interfaces produces the vast majority of echoes visualized throughout the image.

Partial reflection of ultrasound waves occurs when they are incident on interfaces, thereby separating tissues with different acoustic properties. The fraction of the incident energy that is reflected depends on the acoustic impedances of the tissues forming the interface. The acoustic impedance ( Z ) is the speed of sound ( c ) multiplied by the density ( ρ ) of a tissue. The amplitude or strength of the reflected wave is proportional to the difference between the acoustic impedances of tissues forming the interface.

The amplitude reflection coefficient quantifies the relative amplitude of a wave reflected at an interface. It is the ratio of the reflected amplitude to the incident amplitude. For perpendicular incidence of the ultrasound beam on a flat interface ( Fig. 2.5 ), the amplitude reflection coefficient ( R ) is given by:

Reflection at a specular interface. The echo amplitude depends on the difference between the acoustic impedances Z ₁ and Z ₂ of the materials forming the interface.

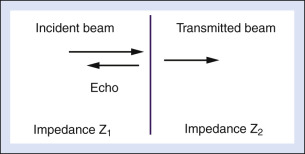
Eq. 2.4 shows that the larger the difference between impedances Z ₂ and Z ₁ , the greater will be the amplitude of the echo from an interface and hence the less will be the transmitted sound into the second medium. Large impedance differences are found at tissue-to-air and tissue-to-bone interfaces. In fact, such interfaces are nearly impenetrable to an ultrasound beam. In contrast, significantly weaker echoes originate at interfaces formed by two soft tissues because, in general, there is not a large difference in impedance between soft tissues.

Smooth, flat interfaces, such as those indicated in Fig. 2.5 , are called specular reflectors (the term specular comes from the Latin for mirror-like ). The direction in which the reflected wave travels after striking a specular reflector is highly dependent on the orientation of the interface with respect to the sound beam. The wave is reflected back toward the source only when the incident beam is perpendicular or nearly perpendicular to the reflector. The amplitude of an echo detected from a specular reflector thus also depends on the orientation of the reflector with respect to the sound beam direction. The ultrasound image in Fig. 2.4 was obtained with a linear array probe, which sends individual ultrasound beams into the scanned region in a vertical direction as viewed on the image. Sections of the vessel wall that are nearly horizontal yield the highest amplitude echoes and hence appear brightest because they were closest to being perpendicular to the ultrasound beams during imaging. Sections where the vessel is slightly inclined appear less bright.

Some soft tissue interfaces are better classified as diffuse reflectors or scatterers of sound. The reflected waves from a diffuse (rough) reflector propagate in multiple directions with respect to the incident beam. Therefore the amplitude of an echo from a diffuse interface is weaker and less dependent on the orientation of the interface with respect to the sound beam than the amplitude detected from a specular reflector (i.e., these reflectors can be imaged without requiring beam perpendicularity).

Scattering

For interfaces whose dimensions are small (with respect to the wavelength) and for rough surfaces, reflections are classified as scattering. Much of the background information viewed in Fig. 2.4 results from scattered echoes, where no single interface can be identified, but echoes from many small interfaces are usually picked up simultaneously. The scattered waves spread in all directions, as illustrated in Fig. 2.6 . Consequently, there is little angular dependence on the strength of echoes detected from scatterers. Unlike the vessel wall, which is a smooth surface best visualized when the ultrasound beam is perpendicular to it, the scatterers are detected with relatively uniform average amplitude from all directions. Echoes resulting from scattering within organ parenchyma are clinically important because they provide much of the diagnostic information seen on ultrasound images and can indicate the condition of the tissue or organ.

Scattering of ultrasound by small heterogeneities.

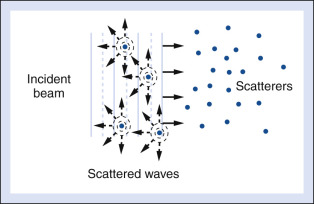
In Doppler ultrasound, blood flow is detected by processing signals resulting from the scattering of sound waves by moving red blood cells. At diagnostic ultrasound frequencies, the size of a red blood cell is very small compared with the ultrasonic wavelength. Scatterers of this size range are called Rayleigh scatterers. The scattered intensity from a distribution of Rayleigh scatterers depends on several factors: (1) the dimensions of the scatterer, with a sharply increasing scattered intensity as the size increases; (2) the number of scatterers present in the beam; (3) the extent to which the density or elastic properties of the scatterer differ from those of the surrounding material; and (4) the ultrasonic frequency. For Rayleigh scatterers, the scattered intensity is proportional to the frequency to the fourth power.

Nonlinear propagation and generation of harmonics

An ultrasound pulse traveling through tissue will undergo distortion with distance if the amplitude is high enough. This is a manifestation of nonlinear sound propagation, and it leads to creation of harmonic frequencies that are multiples of the frequency of the original pulse, contained within the pulse. When partial reflection of the distorted beam occurs at an interface, the reflected echo consists of both the original fundamental frequency and harmonic frequencies. A 3-MHz fundamental echo is accompanied by a 6-MHz second harmonic echo and so on. Higher-order harmonics are possible, but attenuation in tissue usually limits the ability to detect them. Although the second harmonic echoes themselves are of lower amplitude than the fundamental echoes, it is possible to distinguish them from the fundamental in the processor of an ultrasound instrument and to use them to construct an image, called a tissue harmonic image.

A noteworthy characteristic of tissue harmonic images is that they appear less noisy and have fewer artifacts than images made with the fundamental. This is believed to be related to the way the harmonic component of the beam forms (i.e., the harmonics gradually grow in amplitude with increasing depth). The harmonic is not present at the skin surface but gradually develops as the beam propagates deeper into tissue. The second harmonic reaches a peak at some intermediate depth in the patient, then reduces with further increases in depth. Any reverberations or other sources of acoustic noise generated when the transmitted pulse is near the skin surface preferentially contain fundamental frequencies because the harmonics have not built up to any appreciable level at that point. Examples of harmonic images are presented later in this chapter.

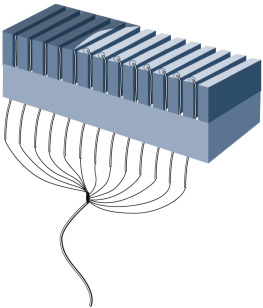
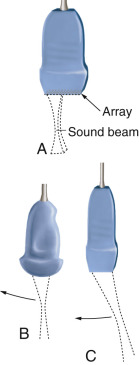
Types of transducers

The operation of three principal types of array transducers is presented in Fig. 2.8 . The most important transducer for peripheral vascular applications is the linear array. Curvilinear arrays and phased arrays are also used in clinics but mainly for imaging deeper structures in the body (e.g., organs such as the liver and kidneys for the former and the heart and intracranial arteries for the latter). Their use in imaging superficial vessels is limited.

Transducer types. (A) Linear array. (B) Curvilinear (convex) array. (C) Phased array.

Detail resolution and slice thickness

Detail (spatial) resolution describes the minimum spacing between two reflectors for which they can be distinguished on the display (i.e., generating separate echoes). Important factors are the axial resolution, the lateral resolution, and the slice thickness. These define a resolution cell, as illustrated in Fig. 2.9 . Like the size of a paintbrush affecting the detail on a painting, the dimensions of the resolution cell ultimately limit the tissue detail that can be resolved on an ultrasound image.

Pulse dimensions emerging from an ultrasound transducer along a single beam line. The pulse duration affects the axial resolution. The width of the beam in the scanning plane determines lateral resolution. The dimensions of the beam perpendicular to the scanning plane determine the slice thickness.

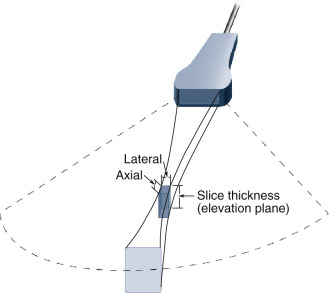
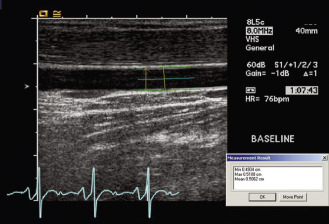
Axial resolution is the ability to resolve (image separately) reflectors that are closely spaced along a sound beam axis . It is determined by the pulse length. Short pulses enable the axial resolution to be 1 mm or less in imaging applications. Damping material attached to the back of the elements helps reduce the pulse duration (and length) and improve axial resolution. Axial resolution is considerably better at higher frequencies ( Fig. 2.10 ) because pulse durations can be made much shorter than at low frequencies. A measurement of the intima-media thickness of a blood vessel requires excellent axial resolution to visualize the interfaces and enable the operator to position the distance measuring cursors for an accurate result ( Fig. 2.11 ).

Images of a test object for determining detail resolution. The reflectors are spaced axially by 2 mm, 1 mm, 0.5 mm, and 0.2 mm. The horizontal row also has reflectors spaced at 2 mm, 1 mm, 0.5 mm, and 0.2 mm. (A) Image obtained at 4 MHz. (B) Image obtained at 11 MHz.

Intima-media thickness measurements in a brachial artery. Axial resolution is important in being able to make these measurements with high precision.

Lateral resolution refers to the closest possible reflector spacing perpendicular to the beam that allows them to be distinguished. It is determined by the width of the ultrasound beam at the location of the reflectors. Beam forming with array imaging systems is a two-step process, first involving shaping a transmitted field and then focusing the sensitivity pattern during echo reception.

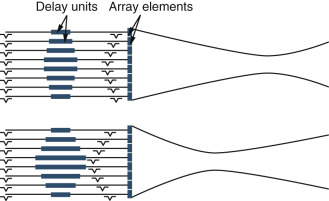
The transmitted field from an individual element would spread quickly with distance if it were driven in isolation because the element is narrow. However, when a group of elements is excited, a directional beam can be formed. This beam can be focused by applying infinitesimal time delays to the transmit pulses applied to individual elements, exciting the outer elements of the group a little earlier than the neighboring inner elements and so on, as shown in Fig. 2.12 . When operators adjust the focus of an instrument, they are changing the focal distance of the transmitted beam. The instrument responds by adjusting the precise arrangement of the time delays applied to the individual elements producing the beam. Focusing narrows the ultrasound beam at the focal depth. Multiple transmit focal depths are also possible. This is done by sending several different transmit pulses along each beam line, each transmit pulse focused at a slightly different depth, retaining and stitching the focal regions into a long focus. Because this requires multiple pulses to form a single beam line on the display, image frame rates are decreased when multiple transmit foci are applied.

Electronic focusing of an array during pulse transmission. By exciting the outer elements of an array group slightly before the inner elements in the sequence shown, the waves from individual elements converge, forming a focused beam. The transmit focal distance is user selectable. More curvature moves the focus toward the transducer. Less curvature moves the focus deeper.

Focusing is also done on the received echoes. After a transmit pulse, echoes are picked up by each element of the active aperture. These are digitized and sent to the digital beam former. The beam former combines the digital signals from each of the array elements and adds them together, forming one extended signal for each transmit pulse. However, the echo from any reflector will need to travel slightly different distances to be picked up by the different array elements. This will create phase differences between the signals from the individual elements. This is corrected by reception focusing, where precisely programmed focusing time delays are applied to the individual signals before summation. The required delay pattern for focusing must change as echoes arrive from progressively greater depths following the transmit pulse. Therefore the reception beam former is designed to adjust the time delays in real time. So-called dynamic reception focusing enables the reception focus of the array to track the depth of the reflector as echoes arrive from increasingly deeper structures. Dynamic reception focusing is not affected directly by the transmit focus adjustment done by the operator but rather is internal to the instrument. Some instruments even run parallel beam formers during reception, creating several dynamically focused received echo beam lines for each transmit pulse.

Focusing reduces the beam width and improves the lateral resolution over a volume called the focal region. The beam width ( W ) in the focal region is approximated by:

Related posts:

Doppler Flow Imaging and Spectral Analysis Ultrasound Assessment Following Endovascular Aortic Aneurysm Repair Ultrasound Assessment of Carotid Stenosis Assessment of Upper Extremity Arterial Disease Ultrasound Assessment Following Endovascular Aortic Aneurysm Repair Evaluation of Organ Transplants

Stay updated, free articles. Join our Telegram channel

Join