Abstract
Objective
This paper describes the relationship between elastic tissue properties and strain and presents an initial investigation of pulse-echo ultrasound to measure two uncorrelated elastic parameters in tissue-mimicking phantoms. The two elastic parameters are the shear modulus, related to deformation of shape, and what we in the paper define as the nonlinear compressibility, related to deformation of volume.
Methods
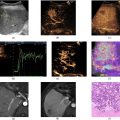
We prepared tissue-mimicking phantoms containing lesions of variable shear modulus and variable nonlinear compressibility. An in-house framework for shear wave imaging was developed using ultrasound radiation force at 4.5 MHz to induce shear waves and plane wave imaging with pulses in a frequency band centered around 12.5 MHz to track the shear waves. For measurements of nonlinear compressibility, co-propagating dual-frequency pulse complexes at 0.7 MHz and 14 MHz were applied. Algorithms were implemented on a Verasonics Vantage ultrasound scanner and a custom-made multi-frequency ultrasound transducer was used. Mechanical indentation measurements were performed to validate ultrasound measurements of the shear modulus. For the nonlinear compressibility, ultrasound measurements were compared to results derived from the literature.
Results
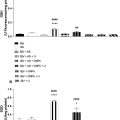
We found good agreement in elasticity results from ultrasound measurements and mechanical indentation as well as when comparing with results derived from the literature.
Conclusion
Results of the current investigation were promising. We plan patient studies involving thyroid lesions and liver steatosis to explore whether measurements of elastic parameters related both to shape deformation and volume deformation are useful in clinical practice.
Introduction
Ultrasound is today a powerful diagnostic tool with numerous clinical applications. Ultrasound imaging can be divided into tissue or anatomical imaging and Doppler imaging. In conventional tissue imaging often referred to as B-mode imaging, the amplitude of the back-scattered signal is typically displayed in a greyscale. When scatterers are moving, the frequency of the back-scattered signals will be altered relative to the transmitted frequency due to the Doppler effect. Ultrasound Doppler imaging enables quantitative or semi-quantitative velocity estimations of moving scatterers, for example in blood flow. Ultrasound B-mode imaging is, however, a qualitative imaging modality. In several clinical situations, this makes detection and diagnosis of pathology difficult, and interpretation of the qualitative images can result in misinterpretation and inter-examiner variability.
Through-transmission of ultrasound, with the possibility of measuring both transmitted and back-scattered signals, opens for quantitative imaging of the acoustic attenuation and the speed of sound with the use of tomographic methods [ ]. Through-transmission of ultrasound is, however, only feasible in very few applications (e.g., breast imaging). Recently, a product for breast tomography ultrasound received FDA approval as an adjunct to breast cancer screening in women with dense breasts [ ].
Manual palpation, which is an important part of the routine physical examination performed by physicians, dates back to ancient Egyptian medicine [ ]. In 1991, external compression was used to form strain images under static conditions and the method was termed elastography by Ophir et al [ ]. Elastography is sometimes referred to as remote palpation and elastography techniques can be divided into static and dynamic methods. For static methods, as developed by Ophir et al, a constant stress is applied to the tissue. The resulting tissue displacements can then be tracked using ultrasound, for example based on correlation techniques. Because the applied stress distribution is unknown, quantitative estimation of an elastic modulus is not feasible with static methods. Dynamic methods are based on ultrasound tracking of shear waves induced either by a mechanical vibrator or by ultrasound radiation force. These methods, which have been developed by several groups [ ], enable quantitative estimations of an elastic modulus.
The importance of nonlinear effects in medical ultrasound was largely neglected until 1980 when two papers were published by Carstensen and Muir [ , ]. Nonlinear effects have now been utilized for more than 2 decades in the form of second harmonic imaging to suppress image noise from pulse reverberations and improve B-mode image quality [ ]. Several groups have worked on methods for tissue characterization based on the coefficient of nonlinearity [ ] but these methods have so far shown limited success and have not been implemented in clinical ultrasound scanners. In 2010, Hansen et al. [ ] suggested using dual-frequency band transmit pulse complexes to better utilize nonlinear acoustics in medical ultrasound and recently the same group published a study demonstrating the use of such pulse complexes to estimate the fat content in tissue-mimicking phantoms [ ].
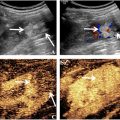
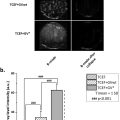
We will describe initial in vitro results for a pulse-echo ultrasound system capable of quantifying two independent elastic parameters, the shear modulus and the nonlinear compressibility. The shear modulus is not an acoustic parameter, but ultrasound waves can be used both to induce shear deformations and to track the propagation of these shear deformations in soft tissues as previously described and shown by several groups. Results from our implementation of shear wave imaging have previously not been published. The nonlinear compressibility is an acoustic parameter and by using dual-frequency band transmit pulses, we can obtain information about this parameter with pulse-echo ultrasound. We have previously published results for this parameter using homogeneous phantoms of different fat content. Here, we present results from heterogenous phantoms and demonstrate detection of lesions with a sharp separation between the lesions and the background. Both parameters are defined below, and the two indicated parameters are in general not correlated. This is important because quantitative estimations of two different elastic parameters with a high degree of correlation would be of limited diagnostic value.
Materials and methods
Longitudinal and shear waves
The shear modulus G?
G
is related to the resistance of a material to undergo a change in shape, a shear deformation, and this material parameter is hence closely related to the characteristics felt by palpation often performed by physicians. The extracellular matrix provides support and facilitates in the dynamic behavior of cells as well as in the regulation of communication between cells. The mechanical properties of the extracellular matrix are controlled by proteins such as collagen and fibrillin which have a high elastic modulus [ ]. Collagen is known to be a major component of the microenvironment in tumors and it has a pivotal role in cancer fibrosis [ ]. Tumors are often characterized as stiff during palpation and the reason for this is typically increased amount of collagen.
The bulk modulus K?
K
is the inverse of the material compressibility κ?
κ
. The bulk modulus is related to the resistance of the material to undergo a change in volume, a volume deformation. For soft tissues, this parameter is typically highly correlated with the mass density [ ].
The net force on an infinitesimal volume element is caused by gradients in surface stresses and this force will exert an acceleration on the indicated volume element. The resulting equation is Cauchy’s equation of motion. Assuming vanishing body forces, it reads
where ρ?
ρ
is the equilibrium mass density, ψi??
ψ i
is particle displacement, σij???
σ i j
are the components of the stress tensor (see Appendix A regarding the relationship between elastic tissue properties and strain). By combining eqns. (1, A.2, A.3) we can derive the general wave equation for an isotropic material
ρ∂2ψi∂t2=(λ+μ)∂2ψj∂xi∂xj+μ∂2ψi∂xj∂xj
where λ?
λ
and μ?
μ
are the Lamé parameters. For a sufficiently smooth and rapidly decaying vector field in three dimensions, we can apply the Helmholtz decomposition theorem [ ] to decompose the displacement vector as the sum of an irrotational field and a solenoidal field
where ψL??
ψ L
and ψS??
ψ S
are the longitudinal and shear components of the particle displacement, respectively. Using this decomposition, eqn (3) can be written
∇[(λ+2μ)∇2φ−ρ∂2φ∂t2]+∇×[μ∇2W−ρ∂2W∂t2]=0
where φ?
φ
is a scalar displacement potential for longitudinal waves, W?
W
is a vector displacement potential for shear waves and where cL??
c L
and cS??
c S
is the propagation speed for longitudinal and shear waves, respectively. Soft tissues other than adipose tissues are typically comprised of approximately 70% of water that fills a matrix of biological molecules having a similar bulk modulus as that of water. For soft tissues, the propagation speed for longitudinal waves is close to that of water, around 1500 ms -1 , and 2–3 orders of magnitude larger than the propagation speed for shear waves. This implies that K≫G?≫?
K ≫ G
and enables the use of longitudinal waves to track the propagation of shear waves. From eqn (8) we notice that the propagation speed for longitudinal waves also depends on the shear modulus ( μ=G?=?
μ = G
) as shown in Appendix A ), and longitudinal waves in a general material are not pressure waves with isotropic stress. However, for a fluid where the shear modulus is equal to zero, we get σ11=σ22=σ33?11=?22=?33
σ 11 = σ 22 = σ 33
, and the longitudinal waves are pressure waves. This is also a good approximation for soft tissues where the longitudinal waves can be treated as pressure waves and for the linear propagation speed we typically use c20=K/ρ?20=?/?
c 0 2 = K / ρ
.
For pressure amplitudes used in medical ultrasound imaging, the mass density does not linearly follow the applied pressure and soft tissues thus show a nonlinear compressibility. By expressing the pressure-density relation as a Taylor series we obtain
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree