6D k-q Space Compressed Sensing for Accelerated High Angular Resolution Diffusion MRI

-space of diffusion signal measurements and fail to take into consideration information redundancy in the 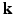$\mathbf {k}$ -space. In this paper, we propose a framework, called 6-Dimensional Compressed Sensing diffusion MRI (6D-CS-dMRI), for reconstruction of the diffusion signal and the EAP from data sub-sampled in both 3D 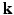$\mathbf {k}$ -space and 3D 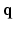$\mathbf {q}$ -space. To our knowledge, 6D-CS-dMRI is the first work that applies compressed sensing in the full 6D 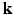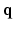$\mathbf {k}$ – $\mathbf {q}$ space and reconstructs the diffusion signal in the full continuous 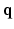$\mathbf {q}$ -space and the EAP in continuous displacement space. Experimental results on synthetic and real data demonstrate that, compared with full DSI sampling in 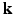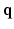$\mathbf {k}$ – $\mathbf {q}$ space, 6D-CS-dMRI yields excellent diffusion signal and EAP reconstruction with low root-mean-square error (RMSE) using 11 times less samples (3-fold reduction in 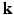$\mathbf {k}$ -space and 3.7-fold reduction in 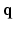$\mathbf {q}$ -space).

1 Introduction

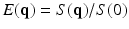Diffusion MRI (dMRI) is a unique non-invasive technique to investigate the white matter in brain. In dMRI, MR signal attenuation $E(\mathbf {q})=S(\mathbf {q})/S(0)$ is a continuous function that depends on the diffusion weighting vector 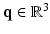$\mathbf {q}\in \mathbb {R}^3$ , where 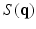$S(\mathbf {q})$ is a diffusion-weighted measurement at 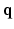$\mathbf {q}$ , and S(0) is the measurement without diffusion weighting at 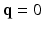$\mathbf {q}=0$ . A central problem in dMRI is to reconstruct the MR signal attenuation 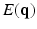$E(\mathbf {q})$ from a limited number of noisy measurements in the 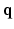$\mathbf {q}$ -space and to estimate some meaningful quantities such as the Ensemble Average Propagator (EAP) and the Orientation Distribution Function (ODF). The EAP 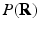$P(\mathbf {R})$ , which is the Fourier transform of 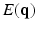$E(\mathbf {q})$ under the narrow pulse assumption [1], fully describes the Probability Density Function (PDF) of water molecule displacements in a voxel. The radial integral of EAP results in the ODF [1], a PDF defined on 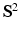$\mathbf {S}^{2}$ . By assuming a Gaussian EAP, Diffusion Tensor Imaging (DTI) requires only a dozen of measurements for estimating the diffusion tensor for the EAP or the diffusion signal. However, it is well reported that DTI cannot fully characterize complex micro-structure such as crossing fibers [1]. On the other hand, Diffusion Spectrum Imaging (DSI) is a model-free technique for EAP estimation. However, DSI normally requires about 515 signal measurements in 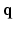$\mathbf {q}$ -space, causing a scan time as long as an hour, thus limiting its clinical utility.

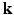Compressed Sensing (CS) [2] is known for its effectiveness in signal reconstruction from a very limited number of samples by leveraging signal compressibility or sparsity. In general, the stronger the assumption is used in reconstruction, the less number of samples is needed. Note that the assumption in CS is always true if the dictionary is devised appropriately to sparsely represent signals. $\mathbf {k}$ -space CS techniques, such as Sparse MRI [3, 4], have been proposed to reconstruct MR images from a sub-sampled 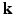$\mathbf {k}$ -space, where the sparsity dictionaries are the wavelet basis and the total variation operator. In dMRI, existing techniques mainly focus on applying CS to the 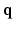$\mathbf {q}$ -space [5–7]. References [5, 6, 8] represented diffusion signal and EAP discretely, which suffers from numerical errors in regridding and numerical integration. References [7, 9, 10] represented diffusion signal and EAP continuously, which have closed form expressions of Fourier transform and ODF/EAP calculation. However, this line of work fails to harness information redundancy in the k-space. The correlation of the 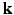$\mathbf {k}$ -space and the 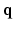$\mathbf {q}$ -space can be employed for even greater sub-sampling, thus further reducing scanning while retaining good reconstruction accuracy. To our knowledge, [11, 12] are the only works on signal and ODF reconstruction in joint 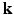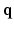$\mathbf {k}$ – $\mathbf {q}$ space by using single-shell data (single b value), i.e., 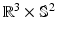$\mathbb {R}^3\times \mathbb {S}^2$ . However, reconstruction of continuous diffusion signal and EAP in whole 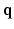$\mathbf {q}$ -space 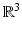$\mathbb {R}^3$ is much more challenging than single shell 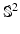$\mathbb {S}^2$ . In this paper, we propose a framework, called 6-Dimensional Compressed Sensing diffusion MRI (6D-CS-dMRI), for reconstruction of the diffusion signal and the EAP from data sub-sampled in both 3D 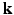$\mathbf {k}$ -space and 3D 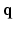$\mathbf {q}$ -space. To our knowledge, 6D-CS-dMRI is the first work that applies compressed sensing in the full 6D 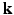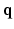$\mathbf {k}$ – $\mathbf {q}$ space and reconstructs the diffusion signal in the full continuous 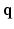$\mathbf {q}$ -space and the EAP in full continuous displacement 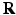$\mathbf {R}$ -space. A preliminary abstract of this work was published in [13].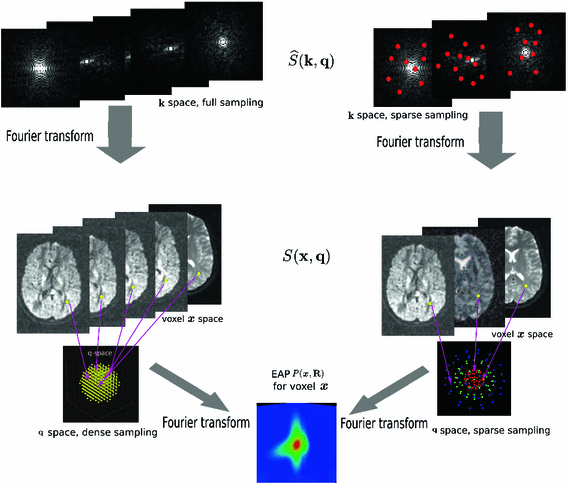

Fig. 1.

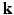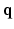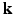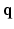Overview of reconstruction in 6D $\mathbf {k}$ – $\mathbf {q}$ space. Dense sampling (left) and sparse sampling (right) in both $\mathbf {k}$ and $\mathbf {q}$ spaces.

2 Compressed Sensing dMRI in Joint k-q Space

2.1 Sampling and Reconstruction in the 6D Joint 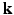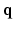$\mathbf {k}$ – $\mathbf {q}$ Space

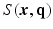Considering the diffusion-attenuated signal $S({{\varvec{x}}},\mathbf {q})$ as a complex function in a 6-dimensional (6D) space, i.e. 3D voxel 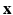$\mathbf {x}$ -space and 3D diffusion 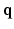$\mathbf {q}$ -space, for a fixed 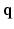$\mathbf {q}$ value, the magnitude of 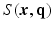$S({{\varvec{x}}},\mathbf {q})$ , denoted as 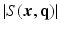$|S({{\varvec{x}}},\mathbf {q})|$ , is a 3D diffusion weighted image volume. Then the 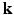$\mathbf {k}$ -space measurements 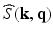$\widehat{S}(\mathbf {k},\mathbf {q})$ and the EAP are related by [14]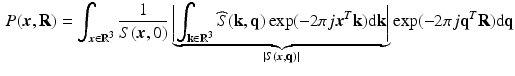

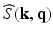$\begin{aligned} P({{\varvec{x}}}, \mathbf {R}) = \int _{{{\varvec{x}}}\in \mathbb {R}^3 } \frac{1}{S({{\varvec{x}}},0)} \underbrace{\left| \int _{\mathbf {k}\in \mathbb {R}^3} \widehat{S}(\mathbf {k},\mathbf {q}) \exp (-2\pi j {{\varvec{x}}}^T\mathbf {k}) \mathrm {d}\mathbf {k}\right| }_{|S({{\varvec{x}}},\mathbf {q})|} \exp (-2\pi j \mathbf {q}^T\mathbf {R})\mathrm {d}\mathbf {q}\end{aligned}$

(1)

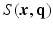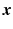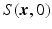where $\widehat{S}(\mathbf {k},\mathbf {q})$ is the 3D Fourier transform of $S({{\varvec{x}}},\mathbf {q})$ over ${{\varvec{x}}}$ , and $S({{\varvec{x}}},0)$ is the image volume with 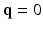$\mathbf {q}=0$ . 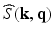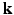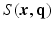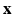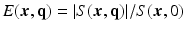Two Fourier transforms are involved: the Fourier transform between $\widehat{S}(\mathbf {k},\mathbf {q})$ in scanning $\mathbf {k}$ -space and $S({{\varvec{x}}},\mathbf {q})$ in voxel $\mathbf {x}$ -space for any fixed $\mathbf {q}$ , and the Fourier transform between $E({{\varvec{x}}}, \mathbf {q})=|S({{\varvec{x}}}, \mathbf {q})|/ S({{\varvec{x}}},0)$ in diffusion 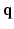$\mathbf {q}$ -space and EAP 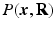$P({{\varvec{x}}},\mathbf {R})$ in displacement 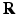$\mathbf {R}$ -space for a voxel 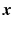${{\varvec{x}}}$ . Instead of dense sampling in 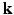$\mathbf {k}$ -space and 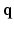$\mathbf {q}$ -space, sparse sampling in both spaces can significantly reduce the scanning time. Figure 1 is an overview of the 6D space sampling and reconstruction framework that will be discussed in this paper. 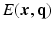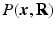The goal is to reconstruct continuous functions $E({{\varvec{x}}},\mathbf {q})$ and $P({{\varvec{x}}},\mathbf {R})$ from a small number of samples of 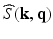$\widehat{S}(\mathbf {k},\mathbf {q})$ in the joint 6D 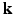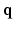$\mathbf {k}$ – $\mathbf {q}$ space.

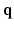A naive approach to 6D-CS-dMRI is to perform two CS reconstructions in association with the two Fourier transforms in Eq. (1). For a fixed $\mathbf {q}$ , Sparse MRI can be used to reconstruct the 3D diffusion weighted (DW) images 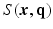$S({{\varvec{x}}},\mathbf {q})$ from samples in 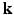$\mathbf {k}$ -space [3]. Then all these 3D DW images can be used in a CS-dMRI technique to reconstruct the EAP [6, 7]. This approach separates the estimation into two independent steps. However, the first step fails to take into consideration the diffusion signal in the same voxel across different 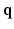$\mathbf {q}$ values, and in the second step, information of different voxels in the same DW images is not used.

2.2 6D-CS-dMRI Using Joint Optimization

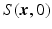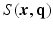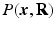We propose a novel reconstruction framework to jointly reconstruct the diffusion signal and EAP from the 6D space. For simplicity, we assume in the following that the baseline image $S({{\varvec{x}}},0)$ is known or pre-reconstructed by Sparse MRI [3]. The goal here is to estimate $S({{\varvec{x}}},\mathbf {q})$ and $P({{\varvec{x}}},\mathbf {R})$ from a number of samples of 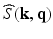$\widehat{S}(\mathbf {k},\mathbf {q})$ in Eq. (1).

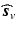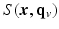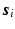We use $\widehat{{{\varvec{s}}}}_v$ to denote the partial Fourier sample vector of the v-th volume $S({{\varvec{x}}},\mathbf {q}_v)$ and ${{\varvec{s}}}_i$ to denote the vector of the diffusion weighted signals 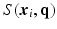$S({{\varvec{x}}}_i,\mathbf {q})$ at voxel i with different 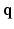$\mathbf {q}$ values. We assume that the magnitude of the diffusion signal vector 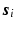${{\varvec{s}}}_i$ can be sparsely represented by a real basis set 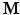$\mathbf M$ and coefficient vector 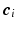${{\varvec{c}}}_i$ , i.e. 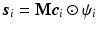${{\varvec{s}}}_i=\mathbf M {{\varvec{c}}}_i \odot \psi _i$ , where 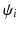$\psi _i$ is the complex vector with unit magnitude that contains phase information, and 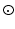$\odot$ means element-wise multiplication. Then we estimate coefficients 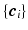$\{{{\varvec{c}}}_i\}$ by solving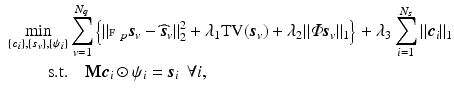

$\begin{aligned} \begin{aligned} \min _{\{{{\varvec{c}}}_i\}, \{{{\varvec{s}}}_v\}, \{\psi _i\} }&\sum _{v=1}^{N_q} \left\{ \Vert \fancyscript{F}_p {{\varvec{s}}}_v - \widehat{{{\varvec{s}}}}_v \Vert _2^2 + \lambda _1 \text {TV}({{\varvec{s}}}_v) + \lambda _2 \Vert \varPhi {{\varvec{s}}}_v \Vert _1 \right\} + \lambda _3 \sum _{i=1}^{N_s} \Vert {{\varvec{c}}}_i\Vert _1 \\ \quad \text {s.t.}&\quad \mathbf M {{\varvec{c}}}_i\odot \psi _i ={{\varvec{s}}}_i \ \ \forall i, \end{aligned} \end{aligned}$

(2)

where

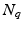is the number of DW images, $$N_s$$

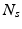is the number of spatial voxels, 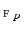$\fancyscript{F}_p$ is the partial Fourier transform operator [3], 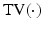$\text {TV}(\cdot )$ denotes the total variation operator, 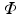$\varPhi$ is a chosen wavelet dictionary. 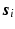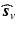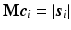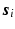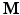Note that ${{\varvec{s}}}_i$ is a complex vector because $\widehat{{{\varvec{s}}}}_v$ is complex, thus the signal representation $\mathbf M {{\varvec{c}}}_i =|{{\varvec{s}}}_i|$ is only applied to the magnitude of ${{\varvec{s}}}_i$ when $\mathbf M$ is a real basis set. The first three terms in Eq. (2) originate from Sparse MRI [3]. The sparsity term of 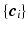$\{{{\varvec{c}}}_i\}$ and the equality constraint are from sparse representation in CS-dMRI [6, 7]. 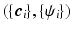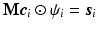Equation (2) is essentially a non-convex optimization problem for variable $(\{{{\varvec{c}}}_i\}, \{\psi _i\})$ , because of the constraints $\mathbf M {{\varvec{c}}}_i\odot \psi _i ={{\varvec{s}}}_i$ , $\forall i$ .