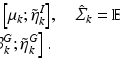(1)
Solution of (1) is to choose the aforementioned eigenvectors of L. The centroid based co-regularization approach as proposed by Kumar et al. [12] formulates the problem of finding a common architecture among multiple subjects, by minimizing the disagreement between subject specific subnetworks and the common subnetworks. Similar to the formulation of spectral clustering, we have the following minimization problem:
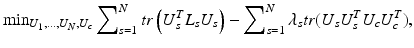
where the centroid eigenvector matrix U c encodes the common set of subnetworks. Eigenvector matrices U s correspond to individual subnetworks of subjects 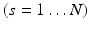 .
. 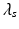 ‘s are the weights of each regularization term. Once this problem is solved for U c , k-means clustering is applied on U c to get the common k subnetworks. The solution is obtained by a two-step iterative scheme after initializing U c : (a) solve for U s by fixing U c and (b) solve for U c by fixing U s . This is repeated until convergence is achieved for U c . Given U c , U s are determined by solving
‘s are the weights of each regularization term. Once this problem is solved for U c , k-means clustering is applied on U c to get the common k subnetworks. The solution is obtained by a two-step iterative scheme after initializing U c : (a) solve for U s by fixing U c and (b) solve for U c by fixing U s . This is repeated until convergence is achieved for U c . Given U c , U s are determined by solving
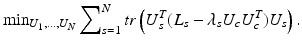
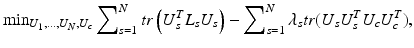
(2)
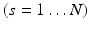 .
. 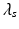 ‘s are the weights of each regularization term. Once this problem is solved for U c , k-means clustering is applied on U c to get the common k subnetworks. The solution is obtained by a two-step iterative scheme after initializing U c : (a) solve for U s by fixing U c and (b) solve for U c by fixing U s . This is repeated until convergence is achieved for U c . Given U c , U s are determined by solving
‘s are the weights of each regularization term. Once this problem is solved for U c , k-means clustering is applied on U c to get the common k subnetworks. The solution is obtained by a two-step iterative scheme after initializing U c : (a) solve for U s by fixing U c and (b) solve for U c by fixing U s . This is repeated until convergence is achieved for U c . Given U c , U s are determined by solving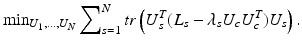
(3)
This is equivalent to calculating eigenvectors corresponding to the smallest k eigenvalues of the modified Laplacian 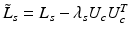 . Then by fixing U s , U c is determined by solving
. Then by fixing U s , U c is determined by solving
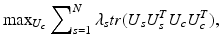
that is again equivalent to finding the eigenvectors corresponding to the largest k eigenvalues of 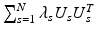 .
.
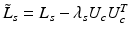 . Then by fixing U s , U c is determined by solving
. Then by fixing U s , U c is determined by solving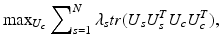
(4)
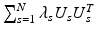 .
.2.2 Reconstructive Projection onto Subnetworks
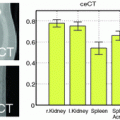
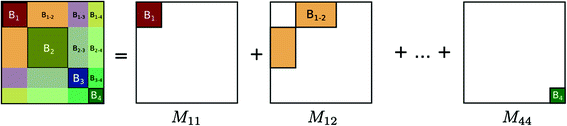
Subnetwork detection determines membership of each anatomical region to a specific subnetwork. Based on these memberships, a connectivity matrix of a subject can be decomposed into blocks (after reordering rows and columns), each corresponding to connections in a subnetwork or between two subnetworks. This is illustrated in Fig. 1. The block structure of a connectivity matrix, as illustrated in Fig. 1, naturally defines a generative model for the multiple subject case: for each block we define a common basis (M ij ) that includes connections in a subnetwork or between two subnetworks, and subject specific coefficients (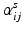 ).
).
 ).
).
Fig. 1.
Decomposition of a connectivity matrix into blocks corresponding to connections in a single subnetwork (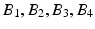 ) or between two subnetworks (
) or between two subnetworks (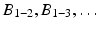 ). Each matrix M ij includes zeros everywhere except at the region corresponding to the encoded block. Note that in case of a single subject, this decomposition defines an exact reconstruction of the original connectivity matrix.
). Each matrix M ij includes zeros everywhere except at the region corresponding to the encoded block. Note that in case of a single subject, this decomposition defines an exact reconstruction of the original connectivity matrix.
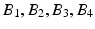 ) or between two subnetworks (
) or between two subnetworks (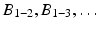 ). Each matrix M ij includes zeros everywhere except at the region corresponding to the encoded block. Note that in case of a single subject, this decomposition defines an exact reconstruction of the original connectivity matrix.
). Each matrix M ij includes zeros everywhere except at the region corresponding to the encoded block. Note that in case of a single subject, this decomposition defines an exact reconstruction of the original connectivity matrix.Then the connectivity matrix A s of a subject s is assumed to be generated as
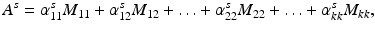
where M ij (corresponding to a block in Fig. 1) defines a common basis of connections in the subnetwork i (if i = j) or between subnetworks i and j (if 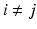 ), including zeros everywhere except at the region corresponding to the connections encoded by M ij . The coefficients
), including zeros everywhere except at the region corresponding to the connections encoded by M ij . The coefficients 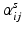 are subject specific weights. The estimation of each M ij can be done independently since they do not share any connection. Thus, each basis component and corresponding coefficients are determined by solving
are subject specific weights. The estimation of each M ij can be done independently since they do not share any connection. Thus, each basis component and corresponding coefficients are determined by solving
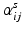 as its sth element. This is solved independently for each M ij by a projected gradient descent algorithm for nonnegative matrix factorization [13]. The solution is found iteratively by updating the current estimate of parameters
as its sth element. This is solved independently for each M ij by a projected gradient descent algorithm for nonnegative matrix factorization [13]. The solution is found iteratively by updating the current estimate of parameters 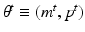 as
as
![$$ \theta^{t + 1} = P[\theta^{t} - \beta^{t} {\nabla }_{\theta } f(\theta^{t} )], $$](/wp-content/uploads/2016/09/A339424_1_En_51_Chapter_Equ7.gif)
![$$ P\left[ x \right]\underline{\underline{\text{def}}} \left\{ {\begin{array}{*{20}l} x \hfill & { if \; l < x < u,} \hfill \\ u \hfill & {if \;x \ge u,} \hfill \\ l \hfill & {if\; x \le l,} \hfill \\ \end{array} } \right. $$](/wp-content/uploads/2016/09/A339424_1_En_51_Chapter_Equ8.gif)
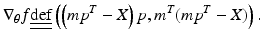




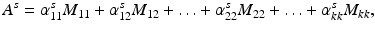
(5)
 ), including zeros everywhere except at the region corresponding to the connections encoded by M ij . The coefficients
), including zeros everywhere except at the region corresponding to the connections encoded by M ij . The coefficients  are subject specific weights. The estimation of each M ij can be done independently since they do not share any connection. Thus, each basis component and corresponding coefficients are determined by solving
are subject specific weights. The estimation of each M ij can be done independently since they do not share any connection. Thus, each basis component and corresponding coefficients are determined by solving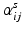 as its sth element. This is solved independently for each M ij by a projected gradient descent algorithm for nonnegative matrix factorization [13]. The solution is found iteratively by updating the current estimate of parameters
as its sth element. This is solved independently for each M ij by a projected gradient descent algorithm for nonnegative matrix factorization [13]. The solution is found iteratively by updating the current estimate of parameters 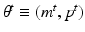 as
as![$$ \theta^{t + 1} = P[\theta^{t} - \beta^{t} {\nabla }_{\theta } f(\theta^{t} )], $$](/wp-content/uploads/2016/09/A339424_1_En_51_Chapter_Equ7.gif)
(7)
![$$ P\left[ x \right]\underline{\underline{\text{def}}} \left\{ {\begin{array}{*{20}l} x \hfill & { if \; l < x < u,} \hfill \\ u \hfill & {if \;x \ge u,} \hfill \\ l \hfill & {if\; x \le l,} \hfill \\ \end{array} } \right. $$](/wp-content/uploads/2016/09/A339424_1_En_51_Chapter_Equ8.gif)
(8)
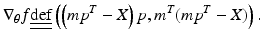
(9)
The step size parameter 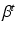 is selected so that the following inequality is satisfied.
is selected so that the following inequality is satisfied.
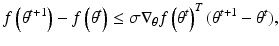
where 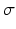 is any value between
is any value between 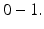 The projection function
The projection function ![$$ P\left[ x \right] $$](/wp-content/uploads/2016/09/A339424_1_En_51_Chapter_IEq13.gif) projects the value of x into the range defined by the lower and upper bounds
projects the value of x into the range defined by the lower and upper bounds 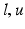 .
.
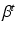 is selected so that the following inequality is satisfied.
is selected so that the following inequality is satisfied.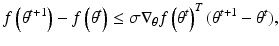
(10)
 is any value between
is any value between  The projection function
The projection function ![$$ P\left[ x \right] $$](/wp-content/uploads/2016/09/A339424_1_En_51_Chapter_IEq13.gif) projects the value of x into the range defined by the lower and upper bounds
projects the value of x into the range defined by the lower and upper bounds 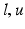 .
.2.3 Population Studies
The coefficients of generative model (5), 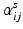 , are subject-specific and encode the overall strength of connections in a subnetwork or between subnetworks. These coefficients that provide a comprehensive low dimensional representation of each subject facilitate population studies. Similar to edge-wise comparison of groups [5], we can compare two groups, such as controls vs. Patients, on a subnetwork-wise basis i.e. we can identify which group has higher/lower expression of a subnetwork or connections of an inter-subnetwork communication. This approach also increases statistical power by lowering the dimensionality of the comparison. Instead of comparing each edge individually, we divide the connectome into subnetworks and compare only coefficients that depict the overall communication pattern of these subnetworks, reducing the problem of multiple comparisons.
, are subject-specific and encode the overall strength of connections in a subnetwork or between subnetworks. These coefficients that provide a comprehensive low dimensional representation of each subject facilitate population studies. Similar to edge-wise comparison of groups [5], we can compare two groups, such as controls vs. Patients, on a subnetwork-wise basis i.e. we can identify which group has higher/lower expression of a subnetwork or connections of an inter-subnetwork communication. This approach also increases statistical power by lowering the dimensionality of the comparison. Instead of comparing each edge individually, we divide the connectome into subnetworks and compare only coefficients that depict the overall communication pattern of these subnetworks, reducing the problem of multiple comparisons.
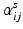 , are subject-specific and encode the overall strength of connections in a subnetwork or between subnetworks. These coefficients that provide a comprehensive low dimensional representation of each subject facilitate population studies. Similar to edge-wise comparison of groups [5], we can compare two groups, such as controls vs. Patients, on a subnetwork-wise basis i.e. we can identify which group has higher/lower expression of a subnetwork or connections of an inter-subnetwork communication. This approach also increases statistical power by lowering the dimensionality of the comparison. Instead of comparing each edge individually, we divide the connectome into subnetworks and compare only coefficients that depict the overall communication pattern of these subnetworks, reducing the problem of multiple comparisons.
, are subject-specific and encode the overall strength of connections in a subnetwork or between subnetworks. These coefficients that provide a comprehensive low dimensional representation of each subject facilitate population studies. Similar to edge-wise comparison of groups [5], we can compare two groups, such as controls vs. Patients, on a subnetwork-wise basis i.e. we can identify which group has higher/lower expression of a subnetwork or connections of an inter-subnetwork communication. This approach also increases statistical power by lowering the dimensionality of the comparison. Instead of comparing each edge individually, we divide the connectome into subnetworks and compare only coefficients that depict the overall communication pattern of these subnetworks, reducing the problem of multiple comparisons.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree