Active Optical Flow Model for Dose Prediction in Spinal SBRT Plans

. These results suggest that the AOFM-based approach is a promising tool for predicting accurate spinal cord dose in clinical practice.

1 Introduction

Spinal tumors are neoplasm located at spinal cords, and most of them are metastases from primary cancers elsewhere [10]. The compression of spinal tumors causes patients to undergo severe pain, and radiation therapy is a primary procedure for pain relief and tumor removal [5]. In contrast to radiation therapy on lung [12] and bladder [11] in which parts of organ can be scarified to ensure tumors receiving maximum dosage, spinal cords are a sensitive serial organ that must be protected because they control the nerve system. Due to this challenge, knowledge-guided dose prediction on spinal cords is seldom addressed.

Fig. 1

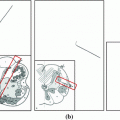
The effects of tumor enclosure on dose distributions. a, b Spinal tumors (marked by red curves) and cords (yellow curves), and c, d corresponding dose distributions, where blue to red means small to large dose values (Color figure online)

Dose levels at spinal cords are mainly caused by the tumor enclosure around the cord in Fig. 1. Dose values within the yellow curve in Fig. 1d are higher than in Fig. 1c because the tumor surrounds the cord more in Fig. 1b in comparison with Fig. 1a. One way to predict dose is therefore to estimate correlation between dose distributions and tumor boundary shapes. Statistical shape analysis can serve this purpose, and it has been extensively studied in the fields of computer vision and medical image analysis [4]. Cootes [2] pioneered this research by applying the principal component analysis (PCA) to a set of landmarks in face images. Active shape model (ASM) was constructed to guide face recognition. Later on, Cootes embedded intensity values and landmark positions into the PCA, which yielded the active appearance model (AAM) [3]. However, both ASM and AAM require extensive labor work to manually select a set of points from each sample image. Rueckert [9] directly imported control points of image deformation fields into the PCA analysis to avoid manual labeling, and the resulting statistical model showed great accuracy in measuring shape variance of a brain image database. Such idea was also extended to 3D irregular heart models to estimate cardiac motion [6]. This method may not directly apply to spinal cord dose prediction because it focused on the statistical description of shape variance to assist organ segmentation and registration. Moreover, ASM established on a set of sparse points cannot meet the accuracy requirements of dose prediction in small spinal cords.

In this paper, we present an active optical flow model (AOFM) to predict dose in spinal cords by (1) applying optical flow to measure the variations at every point of a dose image, (2) importing dose values and optical flow vectors into the PCA analysis, (3) establishing ASM of the tumor contours, and (4) utilizing multiple regression method to compute correlation between AOFM and ASM.

2 Methods

This section elaborates on our framework with respect to data preprocessing, active optical flow model, correlation computation, and dose prediction. In this framework, we treat dose distribution as dose images with intensity at image point representing dose value.

2.1 Data Preprocessing

This step aims to extract a sequence of dose sub-images and tumor contours adjacent to spinal cords from SBRT plans in Fig. 2. AOFM is constructed in the sub-images because dose at spinal cords are only affected by local tumor boundaries.

Fig. 2

Extracting dose sub-images and tumor contours to build AOFM and ASM. a Green rectangle at the cord center illustrates the spatial range of the sub-image, b dose sub-image, and c the red curve representing the tumor contours near the spinal cord (Color figure online)

The size of dose sub-image is 41 $\times$ 41 pixels indicated as a green square in Fig. 2a (approximately 41 mm if intra-spacing is 1.0 mm in the CT images) because the diameter of spinal cord is 10–15 mm and tumors have minor effect on spinal cord if their distance is larger than 10 mm. Thus, 41 pixels are sufficient to include all types of tumors located at different sides of the cord while still preserving the accuracy of measuring the boundary effects on dose prediction. We next extract tumor contours that are adjacent to spinal cords in Fig. 2c because tumors and cord contours are available in the SBRT plan. Finally, all dose sub-images and tumor contours are classified into five groups in terms of spatial relationships between tumors and spinal cords in Fig. 3.

Fig. 3

Five types of spatial relationships between spinal cords and tumors, where dose images are overlaid on the CT images

2.2 Active Optical Flow Model (AOFM)

Dose sub-images are used to compute AOFM, which is essentially a statistical model to describe the dose distributions within a group. Estimating AOFM involves optical flow computation and principal component analysis.

Fig. 4

Process of optical flow computation. a Reference dose image, b current dose image, c transformed current dose image after rigid registration, and d transformed image after optical flow computation

In each group, we randomly choose a dose image $$D_r(x, y)$$

as the reference image (Fig. 4a). Rigid image registration [7] is performed to remove global motion between the reference image and the current dose image (Fig. 4b), and generate the registered image $$D_g(x,y)$$

(Fig. 4c). $$D_g(x,y)$$

is represented in the reference image coordinate, and optical flow computation thus becomes meaningful to measure local deformation between the registered image and the reference image. Let $\mathbf {u}=(u_x,u_y)$ be the optical flow vector at a point $\mathbf {p}=(x,y)$ in the sub-image domain $\varOmega$ . The optical flow computation is formulated as a global energy functional within a variational framework.

$\begin{aligned} E(\mathbf {u})&=\int _\varOmega \bigg (\varPsi (|D_g(\mathbf {p}+\mathbf {u})-D_r(\mathbf {p})|^2) +\alpha \varPsi ({|\nabla D_g(\mathbf {p}+\mathbf {u})-\nabla D_r(\mathbf {p})|^2}) \nonumber \\&\qquad \quad +\beta \varPsi ({|\nabla u_x|^2+|\nabla u_y|^2})\bigg )d\mathbf {p} \end{aligned}$

(1)

where $\varPsi (s^2)=\sqrt{s^2+0.001^2}$ is a modified L1 norm that allows for handling outliers. $\alpha$ and $\beta$ are constant values to balance different terms. Minimizing Eq. 1 generates an optical flow field [1]. Figure 4d gives the result by using optical flow vectors to transform Fig. 4c.

Only gold members can continue reading. Log In or Register to continue