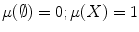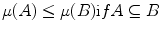a b
b representation have been introduced to overcome these limitations [8].
representation have been introduced to overcome these limitations [8].
In this chapter, both the RGB, L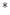 a
a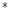 b
b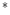 and HSL (hue/saturation/luminance) color space representations will be used for defining spatially adaptive color image filters. The CIE L
and HSL (hue/saturation/luminance) color space representations will be used for defining spatially adaptive color image filters. The CIE L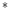 a
a b
b color space is deduced from the CIE XYZ color space:
color space is deduced from the CIE XYZ color space:
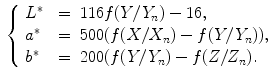
where:
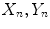 and
and 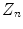 are the CIE XYZ tristimulus values of the reference white point corresponding to the illuminant
are the CIE XYZ tristimulus values of the reference white point corresponding to the illuminant  .
.
 a
a b
b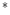 and HSL (hue/saturation/luminance) color space representations will be used for defining spatially adaptive color image filters. The CIE L
and HSL (hue/saturation/luminance) color space representations will be used for defining spatially adaptive color image filters. The CIE L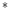 a
a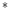 b
b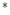 color space is deduced from the CIE XYZ color space:
color space is deduced from the CIE XYZ color space: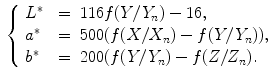
(1)
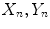 and
and 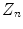 are the CIE XYZ tristimulus values of the reference white point corresponding to the illuminant
are the CIE XYZ tristimulus values of the reference white point corresponding to the illuminant 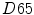 .
.The HSL space is derived from the RGB space by the following equations:
![$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle H&{}=60^{\circ }\times &{}\left\{ \begin{array}{lll} \displaystyle \frac{G-B}{\max (R,G,B)-\min (R,G,B)}&{}\mathrm{ if }&{}R=\max (R,G,B),\\ \displaystyle \frac{B-R}{\max (R,G,B)-\min (R,G,B)}+2&{}\mathrm{ if }&{}G=\max (R,G,B),\\ \displaystyle \frac{R-G}{\max (R,G,B)-\min (R,G,B)}+4&{}\mathrm{ if }&{}B=\max (R,G,B). \end{array}\right. \\ S&{}=&{}\left\{ \begin{array}{lll} \displaystyle \frac{\max (R,G,B)-\min (R,G,B)}{\max (R,G,B)+\min (R,G,B)}&{}\mathrm{ if }&{}L\le 0.5,\\ \displaystyle \frac{\max (R,G,B)-\min (R,G,B)}{2-\max (R,G,B)-\min (R,G,B)}&{}\mathrm{ if }&{}L>0.5. \end{array}\right. \\ \displaystyle L&{}=&{}\displaystyle \frac{\max (R,G,B)+\min (R,G,B)}{2} \end{array}\right. \end{aligned}$$” src=”/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_Equ3.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(3)</DIV></DIV></DIV><br />
<DIV></DIV><br />
<DIV id=Sec4 class=]()
1.3 Need of Vector Order Relations
Rank-order filters (such as morphological filters or Choquet filters) need the use of an order relation between the intensities to be processed. The application of rank-order filtering to color images is not straightforward due to the vectorial nature of the color data. Several vector order relations have been proposed in the literature such as marginal ordering, lexicographical ordering, partial ordering and reduced ordering [2, 6]. For example, let 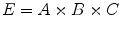 be a color space where
be a color space where 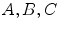 are three sets of scalar values. The lexicographical order on
are three sets of scalar values. The lexicographical order on 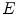 , denoted
, denoted 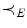 , with the component ordering
, with the component ordering 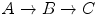 is defined as following for two color vectors
is defined as following for two color vectors 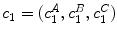 and
and 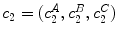 :
:
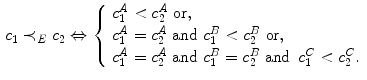
Concerning the vectorial ordering, the lexicographical one will be used in this chapter by fixing the ordering of the components for the three color space representations as follows:
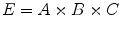 be a color space where
be a color space where 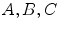 are three sets of scalar values. The lexicographical order on
are three sets of scalar values. The lexicographical order on 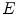 , denoted
, denoted 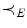 , with the component ordering
, with the component ordering 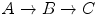 is defined as following for two color vectors
is defined as following for two color vectors 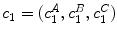 and
and 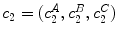 :
: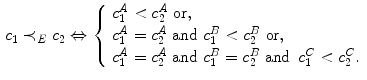
(4)
in RGB: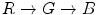 or
or 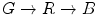
in L a
a b
b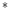 :
: 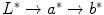
in HSL: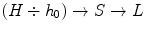 or
or 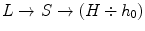 where
where 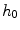 corresponds to the origin of hues and
corresponds to the origin of hues and 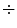 denotes the angular difference defined as:
denotes the angular difference defined as:
2 Color Adaptive Neighborhoods (CANs)
This chapter deals with 2D color images, that is to say image mappings defined on a spatial support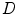 in the Euclidean space
in the Euclidean space 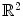 and valued onto a color space
and valued onto a color space 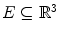 (such as RGB, L
(such as RGB, L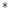 a
a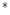 b
b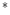 , HSL…). The set of color images is denoted
, HSL…). The set of color images is denoted 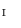 .
.
2.1 Definition
In order to process color images within the GANIP framework, it is first necessary to define Color Adaptive Neighborhoods (CANs) in the most simple way.
For each point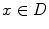 and for a color image
and for a color image 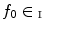 , called the pilot image, the CANs denoted
, called the pilot image, the CANs denoted 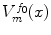 are subsets in
are subsets in 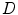 . They are built upon
. They are built upon 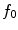 in relation with a homogeneity tolerance
in relation with a homogeneity tolerance 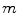 belonging to the positive real value range
belonging to the positive real value range 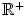 . More precisely,
. More precisely, 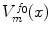 is a subset of
is a subset of  which fulfills two conditions:
which fulfills two conditions:
The CANs are thus mathematically defined as following:
1.
its points have a color value close to that of the point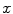 :
: 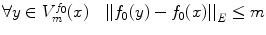 , where
, where 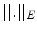 denotes a functional on the color space
denotes a functional on the color space 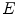 . By using the RGB, L
. By using the RGB, L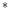 a
a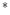 b
b and HSL color spaces, the functionals are defined as [2]:
and HSL color spaces, the functionals are defined as [2]:
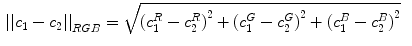
(6)
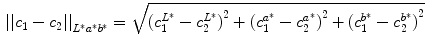
(7)
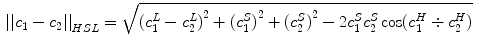
(8)
2.
the set is path-connected with the usual Euclidean topology on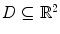 (a set
(a set 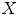 is connected if for all
is connected if for all 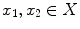 there exists a continuous mapping
there exists a continuous mapping ![$$\tau :[0,1]\rightarrow X$$](/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_IEq56.gif) such that
such that 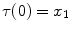 and
and 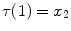 ).
).
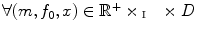
where
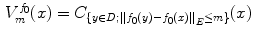
(9) denotes the path-connected component (with the usual Euclidean topology on
denotes the path-connected component (with the usual Euclidean topology on 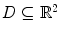 ) of
) of 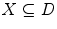 containing
containing 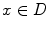 .
.
The definition of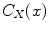 ensures that
ensures that 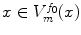 for all
for all 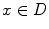 .
.
2.2 Illustration
Figure 1 illustrates the CANs of two points computed on a human retina image (used ad the pilot image ). The figure highlights the homogeneity and the correspondence of the CANs with the spatial structures.
). The figure highlights the homogeneity and the correspondence of the CANs with the spatial structures.
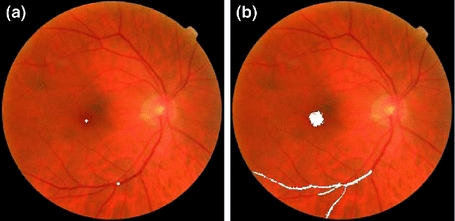
Fig. 1
a Original image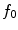 with two seed points
with two seed points 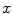 and
and 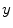 (white dots). b CANs
(white dots). b CANs 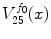 and
and 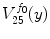 . The CANs of the two selected points of the original color image
. The CANs of the two selected points of the original color image 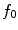 are homogeneous with the tolerance
are homogeneous with the tolerance 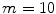 in the RGB color space
in the RGB color space
2.3 Properties
These color adaptive neighborhoods satisfy several properties:
The proofs of these properties are similar to those stated for gray-tone images [11].
1.
reflexivity:
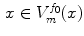
(10)
2.
increasing with respect to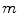 :
:
![$$\begin{aligned} \left( \begin{array}[c]{l} (m_1,m_2) \in \mathbb {R}^+\times \mathbb {R}^+\\ m_1 \le m_2 \end{array} \right) \Rightarrow V_{m_1}^{f_0}(x) \subseteq V_{m_2}^{f_0}(x) \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_Equ11.gif)
(11)
3.
equality between iso-valued points:
![$$\begin{aligned} \left( \begin{array}[c]{l} (x,y) \in D^2\\ x \in V_{m}^{f_0}(y)\\ f_0(x)=f_0(y) \end{array} \right) \Rightarrow V_{m}^{f_0}(x) = V_{m}^{f_0}(y) \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_Equ12.gif)
(12)
3 CAN Choquet Filtering
Fuzzy integrals [9, 36] provide a general representation of image filters. A large class of operators can be represented by those integrals such as linear filters, morphological filters, rank filters, order statistic filters or stack filters. The main fuzzy integrals are Choquet integral [9] and Sugeno integral [36]. Fuzzy integrals integrate a real function with respect to a fuzzy measure.
3.1 Fuzzy Integrals
Let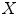 be a finite set. In discrete image processing applications,
be a finite set. In discrete image processing applications, 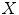 represents the
represents the 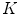 pixels within a subset of the spatial support of the image (an image window). A fuzzy measure,
pixels within a subset of the spatial support of the image (an image window). A fuzzy measure, 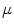 , over
, over 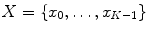 is a function
is a function ![$$\mu :2^X\rightarrow [0,1]$$](/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_IEq81.gif) such that:
such that:
Fuzzy measures are generalizations of probability measures for which the probability of the union of two disjoint events is equal to the sum of the individual probabilities.
The discrete Choquet integral of a function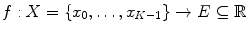 with respect to the fuzzy measure
with respect to the fuzzy measure 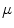 is [26]:
is [26]:
where the subsymbol
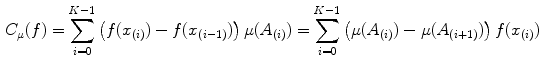
(13)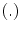 indicates that the indices have been permuted so that:
indicates that the indices have been permuted so that: 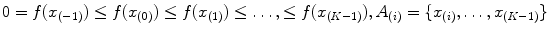 and
and 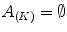 .
.
An interesting property of the Choquet fuzzy integral is that if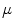 is a probability measure, the fuzzy integral is equivalent to the classical Lebesgue integral and simply computes the expectation of
is a probability measure, the fuzzy integral is equivalent to the classical Lebesgue integral and simply computes the expectation of 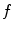 with respect to
with respect to 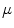 in the usual probability framework.
in the usual probability framework.
The fuzzy integral is a form of averaging operator in the sense that the value of a fuzzy integral is between the minimum and maximum values of the function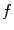 to be integrated.
to be integrated.
3.2 Classical Choquet Filters
Let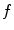 be a color image in
be a color image in 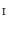 ,
, 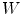 a window of
a window of 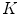 points and
points and 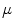 a fuzzy measure defined on
a fuzzy measure defined on 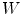 . This measure could be extended to all translated window
. This measure could be extended to all translated window 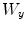 associated to a pixel
associated to a pixel 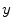 :
: 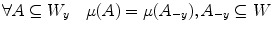 . In this way, the Choquet filter associated to
. In this way, the Choquet filter associated to 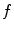 is defined by:
is defined by:
where the subsymbol
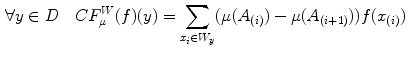
(14) indicates that the indices have been permuted so that:
indicates that the indices have been permuted so that: 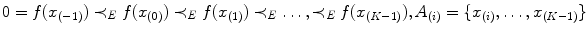 and
and 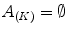 .
.
Note that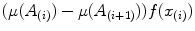 corresponds to the multiplication by
corresponds to the multiplication by 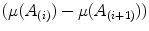 of each component of
of each component of 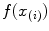 (which is an element of the color space
(which is an element of the color space 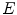 ). The same mapping is realized for the sum
). The same mapping is realized for the sum 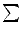 . In this way, the resulting value
. In this way, the resulting value 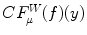 is guaranteed to be in
is guaranteed to be in 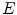 .
.
The Choquet filters generalize [18] several classical filters:
The mean, rank and order filters are Choquet filters with respect to the so-called cardinal measures:
linear filters (mean, Gaussian, …):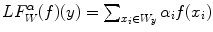 where
where ![$$\alpha \in [0,1]^K,\sum \nolimits _{i=0}^{K-1}\alpha _i=1$$](/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_IEq114.gif)
rank filters (median, min, max, …):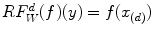 where
where ![$$d \in [0,K-1]\cap \mathbb {N}$$](/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_IEq116.gif)
order filters (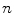 -power,
-power, 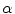 -trimmed mean, quasi midrange, …):
-trimmed mean, quasi midrange, …): 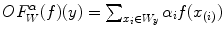 where
where ![$$\alpha \in [0,1]^K,\sum \nolimits _{i=0}^{K-1}\alpha _i=1$$](/wp-content/uploads/2016/03/A308467_1_En_6_Chapter_IEq120.gif)
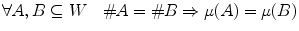 (
(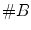 denoting the cardinal of
denoting the cardinal of 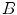 ). Those filters, using an operational window
). Those filters, using an operational window 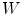 , could be characterized with the application:
, could be characterized with the application: 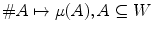 . Indeed, different cardinal measures could be defined for each class of filters:
. Indeed, different cardinal measures could be defined for each class of filters:
In this way, there is a natural link between the weights
mean filter: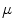 is the fuzzy measure on
is the fuzzy measure on 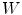 defined by
defined by 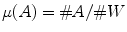
rank filters: (of order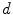 ):
): 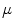 is the fuzzy measure on
is the fuzzy measure on  defined by:
defined by: 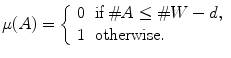
order filters: is the fuzzy measure on
is the fuzzy measure on  defined by
defined by 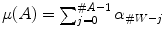
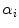 of the general order filters and the fuzzy cardinal measures:
of the general order filters and the fuzzy cardinal measures: 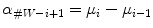 where
where 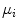 corresponds to the fuzzy measure of the set with cardinal
corresponds to the fuzzy measure of the set with cardinal 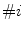 .
.
For example, the median filter (using a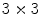 window) is characterized by the following cardinal measure (Fig. 2):
window) is characterized by the following cardinal measure (Fig. 2):
where
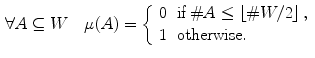
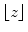 denotes the largest integer not greater than
denotes the largest integer not greater than 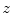 (floor).
(floor).
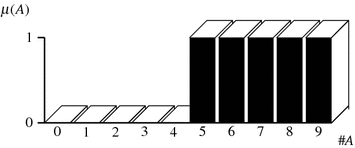
Fig. 2
Fuzzy measure of the classical median filter on a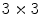 operational window [16]. The corresponding weights of this order filter are equal to
operational window [16]. The corresponding weights of this order filter are equal to 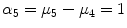 and
and  otherwise
otherwise
The Fig. 3 shows an illustration of several classical filters within the RGB color space, using the square of sizeGet Clinical Tree app for offline access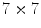 as operational window and the lexicographical order
as operational window and the lexicographical order  . The filters are performed on a painting image of the artist Gamze Aktan.
. The filters are performed on a painting image of the artist Gamze Aktan.
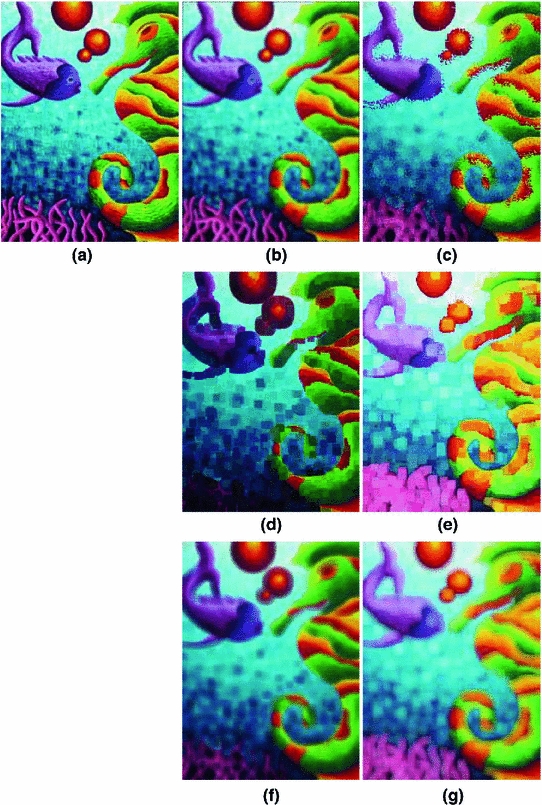
Fig. 3
a Original image. b Classical mean filtering. c Classical median filtering. d Classical min filtering. e Classical max filtering. f Classical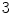 -power filtering. g Classical
-power filtering. g Classical 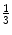 -power filtering. Several classical Choquet filters within the RGB color space, using the square of size
-power filtering. Several classical Choquet filters within the RGB color space, using the square of size 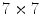

Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree