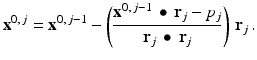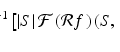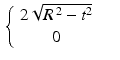(1)
Department of Mathematics and Statistics, Villanova University, Villanova, PA, USA
Electronic supplementary material
The online version of this chapter (doi:10.1007/978-3-319-22665-1_9) contains supplementary material, which is available to authorized users.
9.1 Introduction
To this point, we have studied how Fourier transform methods are used in image reconstruction. This is the approach taken in the seminal work of Cormack [14] and used in the algorithms of today’s CT scan machines. However, the first CT scanner, designed in the late 1960s, by Godfrey Hounsfield, used an approach grounded in linear algebra and matrix theory to generate an image from the machine readings. Algorithms that adopt this point of view are known as algebraic reconstruction techniques, or ART, for short. In this chapter, we look at a few basic mathematical elements of ART.
Where the Fourier transform methods begin with a continuous theory — the filtered back-projection formula of Theorem 6.2 — which is then modeled using discrete methods, ART treats the problem of image reconstruction as a discrete problem from the start. Any image that we produce will be constructed inside a rectangular grid of picture elements, or pixels. The number of pixels in a given image may be large, but it is nonetheless finite, typically on the order of 105. For example, there are 65536 pixels in a 256-by-256 grid. To form an image, a specific color value is assigned to each pixel. For instance, the color value assigned to a given pixel might be a greyscale value, a number between 0 (= black) and 1 (= white), that represents the density or attenuation coefficient of the matter in the sample at the location of the given pixel. ART techniques use a system of constraints derived from the machine readings to compute these color values.
So, suppose an image is to be constructed in a K-by-K grid of pixels. Each pixel is really a small square in the plane. For convenience, number the pixels like so: 1 through K from left to right across the top row; K + 1 through 2K across the second row; and so on until, in the bottom row, we find pixels numbered 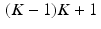 through K 2 . Next, define the pixel basis functions
through K 2 . Next, define the pixel basis functions 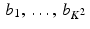 by
by
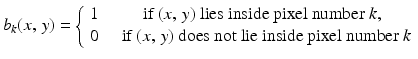
for 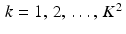 and points (x, y) in the plane. If we assign the color value x k to the k th pixel, then the resulting image will be represented by the function
and points (x, y) in the plane. If we assign the color value x k to the k th pixel, then the resulting image will be represented by the function
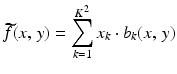
for each point (x, y) lying inside the overall region covered by the grid. Applying the Radon transform 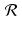 to both sides of this equation, and using the linearity of
to both sides of this equation, and using the linearity of 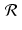 , we get, for each choice of t and
, we get, for each choice of t and 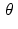 ,
,
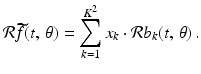
In practice, the X-ray machine gives us the values of 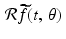 for some finite set of lines
for some finite set of lines 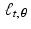 . For convenience, let’s say these known values correspond to
. For convenience, let’s say these known values correspond to 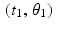 ,
, 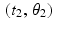 , …,
, …, 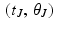 for some positive integer J. Then,
for some positive integer J. Then,
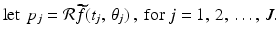 The equation (9.3) can now be written as a system of equations
The equation (9.3) can now be written as a system of equations
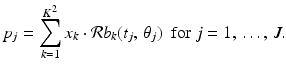
Our next observation is that, since the pixel basis function b k has the value 1 on its pixel and 0 elsewhere, the value of the integral 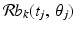 is equal to the length of the intersection of the line
is equal to the length of the intersection of the line 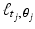 with pixel number k. In principle, these values are easy to compute. (Caveat: If we allow finite-width X-ray beams, rather than zero-width, then this computation becomes more complicated.) So, let’s denote by r j k the length of the intersection of the line
with pixel number k. In principle, these values are easy to compute. (Caveat: If we allow finite-width X-ray beams, rather than zero-width, then this computation becomes more complicated.) So, let’s denote by r j k the length of the intersection of the line 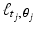 with pixel number k; that is,
with pixel number k; that is,
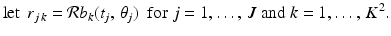
With this notation, the system (9.4) can be written as
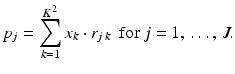
This is a system of J linear equations in K 2 unknowns (x 1, …, 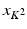 ). Typically, both J and K 2 are on the order of 105, so the system is large. However, any particular line
). Typically, both J and K 2 are on the order of 105, so the system is large. However, any particular line 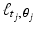 passes through relatively few of the pixels in the grid, on the order of K out of K 2 total pixels. Thus, most of the values r j k are equal to 0, meaning that the system (9.6) is large but sparse. With typical values of J and K, only about one percent of the entries in the coefficient matrix of the system are nonzero.
passes through relatively few of the pixels in the grid, on the order of K out of K 2 total pixels. Thus, most of the values r j k are equal to 0, meaning that the system (9.6) is large but sparse. With typical values of J and K, only about one percent of the entries in the coefficient matrix of the system are nonzero.
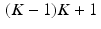 through K 2 . Next, define the pixel basis functions
through K 2 . Next, define the pixel basis functions 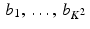 by
by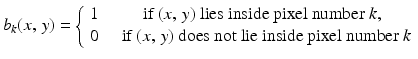
(9.1)
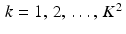 and points (x, y) in the plane. If we assign the color value x k to the k th pixel, then the resulting image will be represented by the function
and points (x, y) in the plane. If we assign the color value x k to the k th pixel, then the resulting image will be represented by the function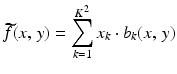
(9.2)
 to both sides of this equation, and using the linearity of
to both sides of this equation, and using the linearity of 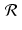 , we get, for each choice of t and
, we get, for each choice of t and 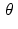 ,
,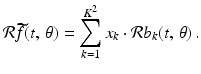
(9.3)
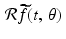 for some finite set of lines
for some finite set of lines 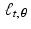 . For convenience, let’s say these known values correspond to
. For convenience, let’s say these known values correspond to 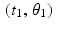 ,
, 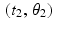 , …,
, …, 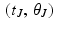 for some positive integer J. Then,
for some positive integer J. Then,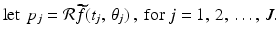
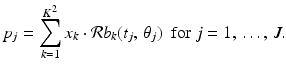
(9.4)
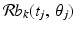 is equal to the length of the intersection of the line
is equal to the length of the intersection of the line 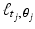 with pixel number k. In principle, these values are easy to compute. (Caveat: If we allow finite-width X-ray beams, rather than zero-width, then this computation becomes more complicated.) So, let’s denote by r j k the length of the intersection of the line
with pixel number k. In principle, these values are easy to compute. (Caveat: If we allow finite-width X-ray beams, rather than zero-width, then this computation becomes more complicated.) So, let’s denote by r j k the length of the intersection of the line 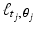 with pixel number k; that is,
with pixel number k; that is,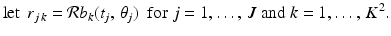
(9.5)
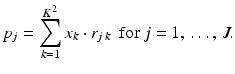
(9.6)
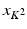 ). Typically, both J and K 2 are on the order of 105, so the system is large. However, any particular line
). Typically, both J and K 2 are on the order of 105, so the system is large. However, any particular line 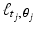 passes through relatively few of the pixels in the grid, on the order of K out of K 2 total pixels. Thus, most of the values r j k are equal to 0, meaning that the system (9.6) is large but sparse. With typical values of J and K, only about one percent of the entries in the coefficient matrix of the system are nonzero.
passes through relatively few of the pixels in the grid, on the order of K out of K 2 total pixels. Thus, most of the values r j k are equal to 0, meaning that the system (9.6) is large but sparse. With typical values of J and K, only about one percent of the entries in the coefficient matrix of the system are nonzero.The system (9.6) can also be expressed in matrix form A x = p by taking A to be the J × K 2 matrix whose jth row is the (row) vector ![$$\,\mathbf{r}_{j} = [r_{j1},\,\ldots,\,r_{jK^{2}}]\,$$](/wp-content/uploads/2016/10/A183987_2_En_9_Chapter_IEq17.gif) , x to be the (column) vector in
, x to be the (column) vector in 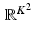 with kth entry x k , and p to be the (column) vector in
with kth entry x k , and p to be the (column) vector in 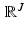 with jth coordinate p j .
with jth coordinate p j .
![$$\,\mathbf{r}_{j} = [r_{j1},\,\ldots,\,r_{jK^{2}}]\,$$](/wp-content/uploads/2016/10/A183987_2_En_9_Chapter_IEq17.gif) , x to be the (column) vector in
, x to be the (column) vector in 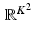 with kth entry x k , and p to be the (column) vector in
with kth entry x k , and p to be the (column) vector in 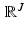 with jth coordinate p j .
with jth coordinate p j .Some computational concerns arise from this approach to the image reconstruction problem. For one thing, the system of equations we have to solve is large — typically on the order of 105 equations. Each sampling of the Radon transform produces an equation in the system while each pixel corresponds to an unknown, the color value for that pixel. If the system of equations is overdetermined, with more equations than unknowns, then the system likely does not have an exact solution. If the system is underdetermined, with more unknowns than equations, then there may be infinitely many solutions, only one of which could possibly be the correct solution. A typical scan might include 200 X-ray measurements at each of 180 different directions, for a total of 36000 equations in the system. A grid of 160 × 160 pixels gives 25600 unknowns and an overdetermined system. To get an image with higher resolution, though, we may want to use a grid of 256 × 256 pixels, or 65536 unknowns. This results in a system that is heavily underdetermined, so the iterative algorithms discussed below are ineffective. For this reason, among others, iterative algorithms are not widely used in commercial CT machines. In any case, due to errors in measurement in sampling the Radon transform, the equations are only estimates to begin with. So, again, the system is not likely to have an exact solution. The fact that the coefficient matrix is sparse, with only a small proportion of nonzero entries, also has a direct effect on the computational complexity.
We now look at several different methods for arriving at an approximate solution to a system of linear equations. The first is an iterative approach called Kaczmarz’s method, while the others are based on least squares approximation.
9.2 Kaczmarz’s method
Kaczmarz’s method is an iterative procedure, or algorithm, for approximating a solution to a linear system A x = p . If we denote by r j the jth row of the matrix A and by p j the jth coordinate of the vector p , then the system A x = p is the same as having 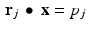 for every value of j . Kaczmarz’s method works by producing a sequence of vectors each of which satisfies one of the individual equations
for every value of j . Kaczmarz’s method works by producing a sequence of vectors each of which satisfies one of the individual equations 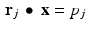 . The first research article to explore the application of algebraic reconstruction techniques to medical imaging was [22], which appeared in 1970. The principal technique employed therein for the reconstruction of images turned out to be the same as Kaczmarz’s method. A further elaboration of this approach can be found in [25].
. The first research article to explore the application of algebraic reconstruction techniques to medical imaging was [22], which appeared in 1970. The principal technique employed therein for the reconstruction of images turned out to be the same as Kaczmarz’s method. A further elaboration of this approach can be found in [25].
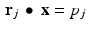 for every value of j . Kaczmarz’s method works by producing a sequence of vectors each of which satisfies one of the individual equations
for every value of j . Kaczmarz’s method works by producing a sequence of vectors each of which satisfies one of the individual equations 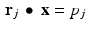 . The first research article to explore the application of algebraic reconstruction techniques to medical imaging was [22], which appeared in 1970. The principal technique employed therein for the reconstruction of images turned out to be the same as Kaczmarz’s method. A further elaboration of this approach can be found in [25].
. The first research article to explore the application of algebraic reconstruction techniques to medical imaging was [22], which appeared in 1970. The principal technique employed therein for the reconstruction of images turned out to be the same as Kaczmarz’s method. A further elaboration of this approach can be found in [25].9.2.1 Affine spaces
Before looking at Kaczmarz’s method itself, we make the following definition.
Definition 9.1.
For a fixed n-dimensional vector r and a number p , the affine space 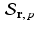 is defined by
is defined by
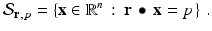
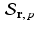 is defined by
is defined by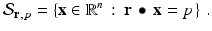
Note that the affine space 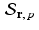 is a subspace of
is a subspace of 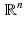 if, and only if, p = 0 .
if, and only if, p = 0 .
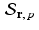 is a subspace of
is a subspace of 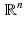 if, and only if, p = 0 .
if, and only if, p = 0 .We have already seen an important example of affine spaces in the lines 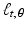 . Each point on
. Each point on 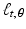 is the terminal point of a vector
is the terminal point of a vector 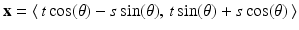 for some value of the parameter s. Letting
for some value of the parameter s. Letting 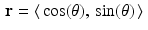 , we compute
, we compute
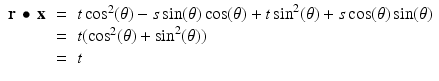 regardless of the value of s . Thus, each line
regardless of the value of s . Thus, each line 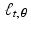 is an affine space. If t = 0 , then
is an affine space. If t = 0 , then 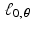 is a line through the origin and, so, is a subspace of
is a line through the origin and, so, is a subspace of 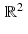 .
.
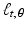 . Each point on
. Each point on 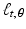 is the terminal point of a vector
is the terminal point of a vector 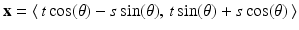 for some value of the parameter s. Letting
for some value of the parameter s. Letting 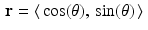 , we compute
, we compute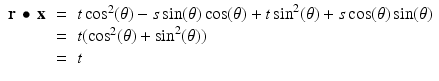
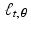 is an affine space. If t = 0 , then
is an affine space. If t = 0 , then 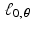 is a line through the origin and, so, is a subspace of
is a line through the origin and, so, is a subspace of 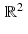 .
.Every affine space can be viewed as a copy of a subspace that has been shifted by a fixed vector. For example, for each fixed value of 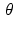 , the line
, the line
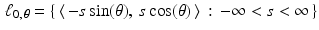 forms a subspace of
forms a subspace of 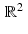 . For each real number t , we then have that
. For each real number t , we then have that
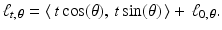
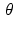 , the line
, the line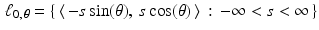
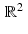 . For each real number t , we then have that
. For each real number t , we then have that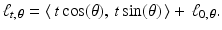
To formulate the same notion slightly differently, let 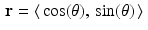 and
and 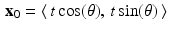 . Then
. Then 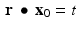 . The subspace
. The subspace 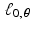 consists of the set of all vectors x for which
consists of the set of all vectors x for which 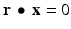 . Thus, the line
. Thus, the line 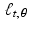 consists of the terminal points of all vectors of the form x 0 + x , where
consists of the terminal points of all vectors of the form x 0 + x , where 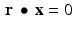 .
.
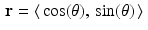 and
and 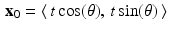 . Then
. Then 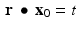 . The subspace
. The subspace 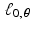 consists of the set of all vectors x for which
consists of the set of all vectors x for which 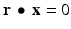 . Thus, the line
. Thus, the line 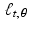 consists of the terminal points of all vectors of the form x 0 + x , where
consists of the terminal points of all vectors of the form x 0 + x , where 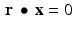 .
.Similarly, for any vector r and any real number p , consider the affine space 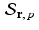 and the subspace
and the subspace 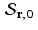 . Observe that, for x 0 and x 1 in
. Observe that, for x 0 and x 1 in 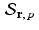 , the vector
, the vector 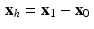 satisfies the homogeneous equation
satisfies the homogeneous equation 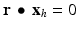 . That is, x h is in the subspace
. That is, x h is in the subspace 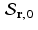 . Since
. Since 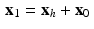 , it follows that every element of the affine space
, it follows that every element of the affine space 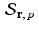 can be obtained by adding the vector x 0 to some element of the subspace
can be obtained by adding the vector x 0 to some element of the subspace 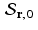 . This is reminiscent of the use of a particular solution together with the general homogeneous solution to obtain the general solution to a nonhomogeneous linear differential equation or a nonhomogeneous system of linear equations.
. This is reminiscent of the use of a particular solution together with the general homogeneous solution to obtain the general solution to a nonhomogeneous linear differential equation or a nonhomogeneous system of linear equations.
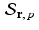 and the subspace
and the subspace 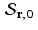 . Observe that, for x 0 and x 1 in
. Observe that, for x 0 and x 1 in 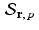 , the vector
, the vector 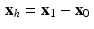 satisfies the homogeneous equation
satisfies the homogeneous equation 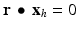 . That is, x h is in the subspace
. That is, x h is in the subspace 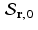 . Since
. Since 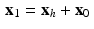 , it follows that every element of the affine space
, it follows that every element of the affine space 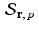 can be obtained by adding the vector x 0 to some element of the subspace
can be obtained by adding the vector x 0 to some element of the subspace 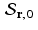 . This is reminiscent of the use of a particular solution together with the general homogeneous solution to obtain the general solution to a nonhomogeneous linear differential equation or a nonhomogeneous system of linear equations.
. This is reminiscent of the use of a particular solution together with the general homogeneous solution to obtain the general solution to a nonhomogeneous linear differential equation or a nonhomogeneous system of linear equations.A final crucial observation is that, since the vector r is orthogonal to the subspace 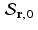 , and, since the affine space
, and, since the affine space 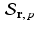 is a parallel translation of this subspace, then it follows that the vector r itself is orthogonal to the affine space
is a parallel translation of this subspace, then it follows that the vector r itself is orthogonal to the affine space 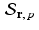 .
.
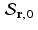 , and, since the affine space
, and, since the affine space 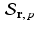 is a parallel translation of this subspace, then it follows that the vector r itself is orthogonal to the affine space
is a parallel translation of this subspace, then it follows that the vector r itself is orthogonal to the affine space 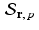 .
.Definition 9.2.
Affine projection. Given a vector u and an affine space 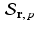 for some vector r and some number p , the affine projection of u in
for some vector r and some number p , the affine projection of u in 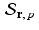 is the vector u ∗ in
is the vector u ∗ in 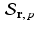 that is closest to u amongst all vectors in
that is closest to u amongst all vectors in 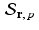 .
.
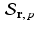 for some vector r and some number p , the affine projection of u in
for some vector r and some number p , the affine projection of u in 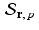 is the vector u ∗ in
is the vector u ∗ in 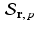 that is closest to u amongst all vectors in
that is closest to u amongst all vectors in 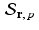 .
.Now, in order to move from u to the closest point in the affine space, it is evident that we should move orthogonally to the affine space. According to our previous observations, this means that we should move in the direction of the vector r itself. Thus, the vector u ∗ that we seek should have the form 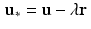 for some number
for some number 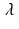 .
.
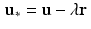 for some number
for some number 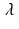 .
.Substituting 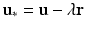 into the equation
into the equation 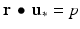 and solving for
and solving for 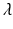 yields
yields
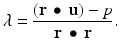 Thus, we have proven the following proposition.
Thus, we have proven the following proposition.
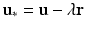 into the equation
into the equation 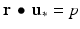 and solving for
and solving for 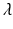 yields
yields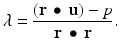
Proposition 9.3.
The affine projection u ∗ of the vector u in the affine space 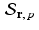 is given by
is given by
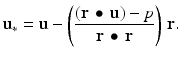
 is given by
is given by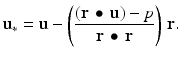
(9.7)
9.2.2 Kaczmarz’s method
Now we put our knowledge of affine spaces to work. In matrix form, let A denote the J × K 2 matrix whose ith row is given by the vector r i , and take p to be the column vector with ith coordinate p i , for i = 1, …, J. Then the equation A x = p describes the linear system in (9.6). Recall that our goal is to find an approximate solution to a linear system A x = p . Again denote the ith row of A by r i and the ith coordinate of p by p i . Then each of the equations 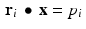 describes an affine space. Kaczmarz’s method proceeds by starting with an initial guess at a solution, a vector of prospective color values, and then computing the affine projection of this initial guess onto the first affine space in our list. This projection is then projected onto the next affine space in the list, and so on until we have gone through the entire list of affine spaces. This constitutes one iteration. The result of this iteration becomes the starting point for the next iteration.
describes an affine space. Kaczmarz’s method proceeds by starting with an initial guess at a solution, a vector of prospective color values, and then computing the affine projection of this initial guess onto the first affine space in our list. This projection is then projected onto the next affine space in the list, and so on until we have gone through the entire list of affine spaces. This constitutes one iteration. The result of this iteration becomes the starting point for the next iteration.
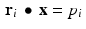 describes an affine space. Kaczmarz’s method proceeds by starting with an initial guess at a solution, a vector of prospective color values, and then computing the affine projection of this initial guess onto the first affine space in our list. This projection is then projected onto the next affine space in the list, and so on until we have gone through the entire list of affine spaces. This constitutes one iteration. The result of this iteration becomes the starting point for the next iteration.
describes an affine space. Kaczmarz’s method proceeds by starting with an initial guess at a solution, a vector of prospective color values, and then computing the affine projection of this initial guess onto the first affine space in our list. This projection is then projected onto the next affine space in the list, and so on until we have gone through the entire list of affine spaces. This constitutes one iteration. The result of this iteration becomes the starting point for the next iteration.In detail, the method proceeds as follows.
(i)
Select a starting guess for x; call it x 0 .
(ii)
Next set 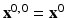 .
.
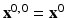 .
.(iii)
(iv)
Note that if the matrix A has J rows, then the vectors x 0, 1, x 0, 2, …, x 0, J will be computed.
(v)
Once x 0, J has been computed, define 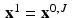 and begin the process again starting with x 1 . That is, now set
and begin the process again starting with x 1 . That is, now set 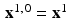 and compute the vectors x 1, 1 ,
and compute the vectors x 1, 1 , 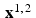 , …, x 1, J , as in (9.8).
, …, x 1, J , as in (9.8).
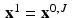 and begin the process again starting with x 1 . That is, now set
and begin the process again starting with x 1 . That is, now set 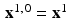 and compute the vectors x 1, 1 ,
and compute the vectors x 1, 1 , 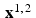 , …, x 1, J , as in (9.8).
, …, x 1, J , as in (9.8).(vi)
Then let 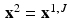 and repeat the process starting with
and repeat the process starting with 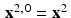 .
.
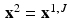 and repeat the process starting with
and repeat the process starting with 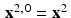 .
.(vii)
Stop when we’ve had enough!
There are, as we might expect, some computational concerns with this method. In principle, the successive vectors x 0 , x 1 , x 2 , … should get closer to a vector that satisfies the original system A x = p. However, the convergence may be quite slow, meaning that many steps of the iteration would have to be applied to get a good approximant. Also, if the system has no solution, then the vectors computed from the algorithm might settle into a specific pattern, called an attractor in dynamical systems theory, or might even exhibit chaotic behavior.
Example 9.4.
Apply Kaczmarz’s method to the system consisting of just the two lines 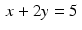 and
and 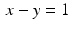 . So
. So 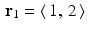 ,
, 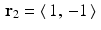 , p 1 = 5 , and p 2 = 1 . With the initial guess
, p 1 = 5 , and p 2 = 1 . With the initial guess 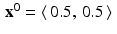 , the diagram on the left in Figure 9.1 shows that the solution
, the diagram on the left in Figure 9.1 shows that the solution 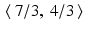 will quickly be found.
will quickly be found.
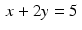 and
and 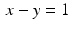 . So
. So 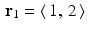 ,
, 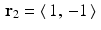 , p 1 = 5 , and p 2 = 1 . With the initial guess
, p 1 = 5 , and p 2 = 1 . With the initial guess 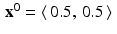 , the diagram on the left in Figure 9.1 shows that the solution
, the diagram on the left in Figure 9.1 shows that the solution 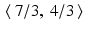 will quickly be found.
will quickly be found.
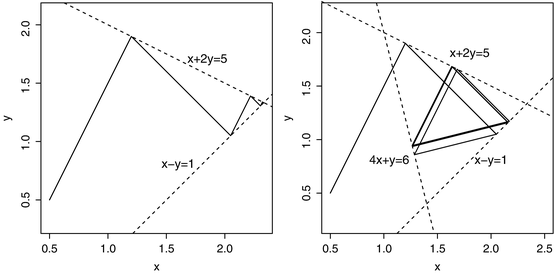
Fig. 9.1
On the left, Kaczmarz’s method converges quickly to the point of intersection of two lines. On the right, the successive iterations settle into a triangular pattern for a system of three lines.
However, when we include the third line 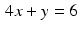 (so
(so 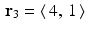 and p 3 = 6 ), then the successive iterations settle into a triangular pattern, shown in the diagram on the right in the figure.
and p 3 = 6 ), then the successive iterations settle into a triangular pattern, shown in the diagram on the right in the figure.
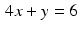 (so
(so 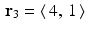 and p 3 = 6 ), then the successive iterations settle into a triangular pattern, shown in the diagram on the right in the figure.
and p 3 = 6 ), then the successive iterations settle into a triangular pattern, shown in the diagram on the right in the figure.Example with R 9.5.
In an implementation of Kaczmarz’s method, one can choose to save only the last estimate of the solution, after all cycles have been completed. Alternatively, one can generate a matrix where each successive row is an intermediate estimate, either from a single equation or from a full cycle. We present two versions here. The first approach is applied to the systems of equations in Example 9.4 and was used to produce Figure 9.1.
##Kaczmarz method: save next estimate from each eqn.
kacz.v0=function(mat,rhs,ncycles){
neq=nrow(mat)
V=matrix(double((neq*ncycles+1)*ncol(mat)),
neq*ncycles+1,ncol(mat))
V[1,]=rep(0.5,2)
for (i in 1:ncycles){
for (j in 1:neq){
V[neq*(i-1)+j+1,]=ifelse(mat[j,]==0,V[neq*(i-1)+j,],
V[neq*(i-1)+j,]-((sum(V[neq*(i-1)+j,]*mat[j,])-
rhs[j])/sum(mat[j,]*mat[j,]))*mat[j,])}}
list(V=V)}
##For Figure 09_1
R1=matrix(c(1,2,1,-1),2,2,byrow=T)#2 lines
p1=c(5,1)
V1=kacz.v0(R1,p1,2)$V
R2=matrix(c(1,2,1,-1,4,1),3,2,byrow=T)#3 lines
p2=c(5,1,6)
V2=kacz.v0(R2,p2,3)$V
#plot fig09_1a
plot(V1[,1],V1[,2],type=”l”,lwd=2,xlab=”x”,ylab=”y”)
plot(V2[,1],V2[,2],type=”l”,asp=1,xlab=”x”,ylab=”y”,lwd=2)
In our second version of Kaczmarz’s method, all intermediate estimates are computed, but only the final estimate is saved. This version will be used in the CT scan image reconstructions that follow.
##Kaczmarz’s method; save only most recent estimate
kaczmarz.basic=function(mat,rhs,numcycles){
numeq=nrow(mat)
sol.est=rep(0.5,ncol(mat))#initial “guess” of all 0.5s
for (i in 1:numcycles){
for (j in 1:numeq){
sol.est=ifelse(mat[j,]==0,sol.est,sol.est-
((sum(sol.est*mat[j,])-rhs[j])/sum(mat[j,]*mat[j,]))*
mat[j,])
}}list(sol.est=sol.est)}
Before looking at an image created using Kaczmarz’s method, we state, without proof, the main convergence theorem for this algorithm. (For a proof, see [17] or [39].)
Theorem 9.6.
If the linear system A x = p has at least one solution, then Kaczmarz’s method converges to a solution of this system. Moreover, if x 0 is in the range of A T , then Kaczmarz’s method converges to the solution of minimum norm.
The convergence result in Theorem 9.6 generally is not relevant in medical imaging, where the linear systems encountered tend to be indeterminate and where, in any case, it is computationally feasible to run only a few iterations of Kazcmarz’s method.
The images in Figure 9.2 are reconstructions of the crescent-shaped phantom illustrated in Figure 2.8 and defined by the attenuation function in (2.11). For each image, five full iterations of Kaczmarz’s method were applied with an initial vector x 0 having every coordinate equal to 0. 5 . (In other words, the starting point was taken to be a neutral grey image.) For the coarser image, the Radon transform of the phantom was sampled using Δ t = 0. 05 on the interval − 1 ≤ t ≤ 1 , with angle increments of 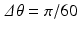 , for a total of 2460 different values. The corresponding system of equations, (9.6), is overdetermined in this case. The second image has a grid with 10000 pixels and used Δ t = . 02 and
, for a total of 2460 different values. The corresponding system of equations, (9.6), is overdetermined in this case. The second image has a grid with 10000 pixels and used Δ t = . 02 and 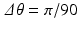 , for a total of 9090 values of the Radon transform. With these settings, the system (9.6) is underdetermined. These images show the crescent, but do not necessarily compare favorably to the reconstructions in Figures 8.8 and 8.9.
, for a total of 9090 values of the Radon transform. With these settings, the system (9.6) is underdetermined. These images show the crescent, but do not necessarily compare favorably to the reconstructions in Figures 8.8 and 8.9.

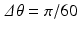 , for a total of 2460 different values. The corresponding system of equations, (9.6), is overdetermined in this case. The second image has a grid with 10000 pixels and used Δ t = . 02 and
, for a total of 2460 different values. The corresponding system of equations, (9.6), is overdetermined in this case. The second image has a grid with 10000 pixels and used Δ t = . 02 and 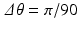 , for a total of 9090 values of the Radon transform. With these settings, the system (9.6) is underdetermined. These images show the crescent, but do not necessarily compare favorably to the reconstructions in Figures 8.8 and 8.9.
, for a total of 9090 values of the Radon transform. With these settings, the system (9.6) is underdetermined. These images show the crescent, but do not necessarily compare favorably to the reconstructions in Figures 8.8 and 8.9.
Fig. 9.2
Kaczmarz’s method applied to a crescent-shaped phantom: On the left, a 40 × 40 image grid and 2460 values of the Radon transform; on the right, a 100 × 100 image grid and 9090 values of the Radon transform.
Example with R 9.7.
To create an image from X-ray data using Kaczmarz’s method, as in Figure 9.2, we must compute the matrix whose entries are the lengths of the intersections of the lines in the scan with the pixels in the image grid. Since each pixel is a small square, we can follow the basic approach from Example 2.15 above to compute each entry of the coefficient matrix. In R, it is convenient to encode this as a function of the set of lines and the locations of the pixels. For instance, if the general procedure is radon.pix, then the output for a specific scan and selected image grid might be
rad.mat=radon.pix(grid.theta,grid.t,grid.cx,grid.cy)$coef.
Next, the right-hand sides are the X-ray data values from the scan, or, in this exercise, the values of the Radon transform of a phantom. Notice that the coefficient matrix can be re-used, while the right-hand sides will change with each scan. The color values for the image are computed by applying the procedure kaczmarz.basic from Example 9.5. (In this exercise, rad.mat is the coefficient matrix just computed and rp1 is the vector of X-ray data for the phantom. Then image.mat is the matrix of color values.)
sys2=kaczmarz.basic(rad.mat,rp1,5)$sol.est
image.mat=matrix((sys2-min(sys2))/(max(sys2)-min(sys2)),
nrow=K,byrow=T)
Finally, we plot each pixel using the polygon command, seen in Example 1.1. This time, each square pixel is its own polygon. The grid is defined by the sets xval and yval of x– and y-coordinates, respectively.
plot(c(-1,1), c(-1,1), type = “n”,axes=””,asp=1)
for (i in 1:K){
for (j in 1:K){
polygon(c(xval[j],xval[j+1],xval[j+1],xval[j],xval[j]),
c(yval[i],yval[i],yval[i+1],yval[i+1],i),
col = gray(image.mat[i,j]),border = NA)}}
One concern about the use of Kaczmarz’s method in the context of tomography, as mentioned before, is that the sheer size of the system of equations involved can be an impediment. Also, each of the values r jk represents the length of the intersection of one of the X-ray beams with one of the pixel squares in the image grid. Thus, as observed before, most of these values are zeros. The formula for computing 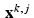 from
from 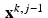 only alters x k, j−1 in those components that correspond to the pixels through which the jth beam passes. To streamline the computation of
only alters x k, j−1 in those components that correspond to the pixels through which the jth beam passes. To streamline the computation of 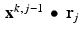 , we could store the locations of the nonzero entries of r j . In its favor, Kaczmarz’s method can be applied to the fan beam and cone beam geometries without re-binning the scanner data, since each X-ray in the scan simply defines another affine subspace in the system.
, we could store the locations of the nonzero entries of r j . In its favor, Kaczmarz’s method can be applied to the fan beam and cone beam geometries without re-binning the scanner data, since each X-ray in the scan simply defines another affine subspace in the system.
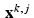 from
from 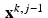 only alters x k, j−1 in those components that correspond to the pixels through which the jth beam passes. To streamline the computation of
only alters x k, j−1 in those components that correspond to the pixels through which the jth beam passes. To streamline the computation of 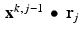 , we could store the locations of the nonzero entries of r j . In its favor, Kaczmarz’s method can be applied to the fan beam and cone beam geometries without re-binning the scanner data, since each X-ray in the scan simply defines another affine subspace in the system.
, we could store the locations of the nonzero entries of r j . In its favor, Kaczmarz’s method can be applied to the fan beam and cone beam geometries without re-binning the scanner data, since each X-ray in the scan simply defines another affine subspace in the system.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree