Calculation of the liver absorbed dose is in Gy delivered after injection:
(2)
![$$ {\mathbf{Liver}} \, {\mathbf{Dose}} \, \left( {{\mathbf{Gy}}} \right) = \frac{{50 \, \left[ {{\text{Injected Activity }}\left( {\text{GBq}} \right)} \right]\left[ { 1- F} \right]}}{{{\text{Mass of Selected Liver Target }}\left( {\text{kg}} \right)}} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equb.gif)
![$$ {\mathbf{Liver}} \, {\mathbf{Dose}} \, \left( {{\mathbf{Gy}}} \right) = \frac{{50 \, \left[ {{\text{Injected Activity }}\left( {\text{GBq}} \right)} \right]\left[ { 1- F} \right]}}{{{\text{Mass of Selected Liver Target }}\left( {\text{kg}} \right)}} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equb.gif)
where F is the fraction of injected activity deposited into the lungs as measured by Tc-99 MAA. In these equations for glass microspheres F = 0.61 when GBq is used, (representing the upper limit of activity that can safely be delivered to the lungs in a single glass microsphere administration) to estimate the fraction of dose that could be deposited into the lungs.
Many factors are taken into consideration when determining the activity to use for an individual patient. The formulae above have been clinically verified in more than 2,000 patients over the past 10 years. However, there are limitations in using the MIRD convention. It is not the case that microspheres are uniformly deposited in the treatment volume; in fact from the preclinical and human clinical data it is very much the opposite. However, the MIRD formulae do enable microspheres to develop confidence in the range of activity that is suggested by these conventions, and must use their experience, skill and collaborative medical expertise to choose the most appropriate activity for a particular patient.
4.3 Resin Microspheres
Because resin microspheres carry less activity (50–80 Bq/sphere on average when delivered to patient) compared to glass microspheres, many more are used to deliver an adequate dose tumor. The typical patient receives about 15–20 million spheres for a 1.5–2 GBq activity distributed in both lobes of the liver. This can cause temporary embolic side effects (pain, fever, nausea), which are similar but far less intense than is seen in TACE post embolic symptoms. However, not all hepatic vascular beds can accept the number of microspheres desired from the pre treatment planning formulae, and thus the delivery of microspheres discontinued prior to completely emptying the volume of microspheres planned. It is not the desire or intent to perform an embolic treatment, rather it is a brachytherapy procedure and therefore it is recommended that the delivery of microspheres not cause stasis and/or reflux. Optimal implantation of microspheres is for the tumor-only to have spheres, and the normal adjacent liver free of radiation. Once stasis has occurred however, the normal liver arteries have also been filled with microspheres and the selectivity and therapeutic benefit to brachytherapy is lost. If the whole lobe or segment is receiving the same dose of radiation (tumor and normal liver) than external beam radiation could have been used instead. Also, many patients are selected for microsphere therapy specifically because an embolic treatment was not felt to be safe or in their best interests.
The manufacturer’s User’s Manual3 suggests three methods of estimating the activity to use for resin microsphere treatment: (I) Body Surface Area method (BSA), (II) Empiric method, and (III) Partition method (Ho et al. 1996, 1997) (Eq. 3), appears in the manual as Eq. 3. The manufacturer’s recommendation for the use of Eq. 3 did not appear to be intended for diffuse tumors; however the guidelines regarding the appropriateness of this equation are unclear. Therefore, we tested its application for all tumor types.
To better understand the following activity calculations (Toohey et al. 2000; Gulec et al. 2006a; Stabin 2006; Stabin and Konijnenberg 2000), a brief review is shown of the schema developed by the Medical Internal Radiation Dose (MIRD) Committee of the Society of Nuclear Medicine (Toohey et al. 2000).
In this formalism the dose rate, 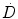 can be written as
can be written as
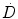 can be written as
can be written as(1)
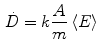
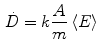
where k is a constant to yield the dose rate in desired units, A is the source activity, m is the mass of tissue that the radiation is absorbed within, and 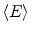 is the average energy emitted per nuclear transition. Since we are dealing with a source undergoing nuclear decay, the activity of the source is not constant in time. Also the source is permanently implanted in the patient with no biologic excretion. Thus the activity as a function of time is described by the radioactive decay equation.
is the average energy emitted per nuclear transition. Since we are dealing with a source undergoing nuclear decay, the activity of the source is not constant in time. Also the source is permanently implanted in the patient with no biologic excretion. Thus the activity as a function of time is described by the radioactive decay equation.
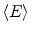 is the average energy emitted per nuclear transition. Since we are dealing with a source undergoing nuclear decay, the activity of the source is not constant in time. Also the source is permanently implanted in the patient with no biologic excretion. Thus the activity as a function of time is described by the radioactive decay equation.
is the average energy emitted per nuclear transition. Since we are dealing with a source undergoing nuclear decay, the activity of the source is not constant in time. Also the source is permanently implanted in the patient with no biologic excretion. Thus the activity as a function of time is described by the radioactive decay equation.(2)
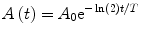
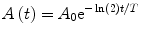
where A 0 is the calibrated activity, t is the time from calibration, and T is the half-life of the radioactive source. The absorbed dose, calculated by integrating over all time, is then given by the following
(3)
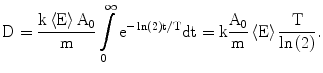
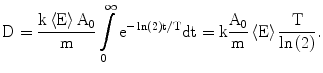
From the published 90Y decay data, the average energy released in the  decay of 90Y is 0.9267 MeV (Bq s)−1, assuming that all of the energy of the
decay of 90Y is 0.9267 MeV (Bq s)−1, assuming that all of the energy of the  decay is absorbed in tissue. Using the half-life T = 64.04 h, the total radiation absorbed dose after the complete
decay is absorbed in tissue. Using the half-life T = 64.04 h, the total radiation absorbed dose after the complete  decay of 90Y is given by
decay of 90Y is given by
![$$ D [ {\text{Gy]}} = 4 9. 3 8\frac{{A_{ 0} [ {\text{GBq]}}}}{{m [ {\text{kg]}}}}. $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equf.gif)
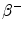 decay of 90Y is 0.9267 MeV (Bq s)−1, assuming that all of the energy of the
decay of 90Y is 0.9267 MeV (Bq s)−1, assuming that all of the energy of the 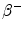 decay is absorbed in tissue. Using the half-life T = 64.04 h, the total radiation absorbed dose after the complete
decay is absorbed in tissue. Using the half-life T = 64.04 h, the total radiation absorbed dose after the complete 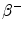 decay of 90Y is given by
decay of 90Y is given by![$$ D [ {\text{Gy]}} = 4 9. 3 8\frac{{A_{ 0} [ {\text{GBq]}}}}{{m [ {\text{kg]}}}}. $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equf.gif)
The difference between the 49.38 constant given here and the 49670 constant given below is explained by taking the mass in kg instead of g and current values for the average energy released in the decay process.
I.
Body Surface Area Method Calculation (Eqs. 1 – 5)
1.
![$$ {\text{BSA}}\left[ {{\text{m}}^{2} } \right] = 0.20247 \times \left( {{\text{height}}\left[ {\text{m}} \right]} \right)^{0.725} \times \left( {{\text{weight}}\left[ {\text{kg}} \right]} \right)^{0.425} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equg.gif)
![$$ {\text{BSA}}\left[ {{\text{m}}^{2} } \right] = 0.20247 \times \left( {{\text{height}}\left[ {\text{m}} \right]} \right)^{0.725} \times \left( {{\text{weight}}\left[ {\text{kg}} \right]} \right)^{0.425} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equg.gif)
2.
![$$ {\text{A}}\left[ {\text{GBq}} \right] = \left( {{\text{BSA}} -
0.2} \right) +
\frac{{{\text{vol}}\,{\text{of}}\,{\text{tumor}}}}{{{\text{vol}}\,{\text{of}}\,{\text{tumor}}
+ {\text{vol}}\,{\text{of}}\,{\text{liver}}}} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equh.gif)
![$$ {\text{A}}\left[ {\text{GBq}} \right] = \left( {{\text{BSA}} -
0.2} \right) +
\frac{{{\text{vol}}\,{\text{of}}\,{\text{tumor}}}}{{{\text{vol}}\,{\text{of}}\,{\text{tumor}}
+ {\text{vol}}\,{\text{of}}\,{\text{liver}}}} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equh.gif)
3.
![$$ A\left[ {\text{GBq}} \right]_{\text{resin}}\,=
\frac{{D_{\text{liver}} \left( {\left( {T :N \times M_{\text{tumor}}
} \right) + M_{\text{liver}} } \right)}}{{49670\left( {1 - L / 1 0
0} \right)}}. $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equi.gif)
![$$ A\left[ {\text{GBq}} \right]_{\text{resin}}\,=
\frac{{D_{\text{liver}} \left( {\left( {T :N \times M_{\text{tumor}}
} \right) + M_{\text{liver}} } \right)}}{{49670\left( {1 - L / 1 0
0} \right)}}. $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equi.gif)
D liver
Nominal dose (Gy) to the liver
T:N
Tumor to normal ratio was calculated (see below)
L
Shunt fraction (%) of microspheres from liver to lung based on macro agglutinated albumin (MAA) nuclear medicine scan
M liver
Total mass of liver (g) from CT volume
M tumor
Total mass of tumor (g) from CT volume
49670
Absorbed dose conversion constant from infinite decay
V T
cc from CT scan
V L
cc from CT scan
4.
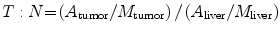
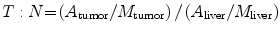
A tumor
Activity in tumor from MAA scan
A liver
Activity in liver from MAA scan
M liver
Mass in g of normal liver (excluding tumor) from CT scan
M tumor
Mass in g of tumor in liver (excluding normal liver tissue) from CT scan
5.
![$$ L\left[ {{\text{Lung}}\,{\text{Shunt}}\,\% } \right] = \frac{{{\text{RO}}IL{\text{ung}}\,{\text{Counts}} \times 1 0 0}}{{{\text{RO}}IL{\text{ung}}\,{\text{Counts}} + {\text{RO}}IL{\text{iver}}\,{\text{Counts}}}} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equk.gif)
![$$ L\left[ {{\text{Lung}}\,{\text{Shunt}}\,\% } \right] = \frac{{{\text{RO}}IL{\text{ung}}\,{\text{Counts}} \times 1 0 0}}{{{\text{RO}}IL{\text{ung}}\,{\text{Counts}} + {\text{RO}}IL{\text{iver}}\,{\text{Counts}}}} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equk.gif)
II.
Empiric Method Calculation
Tumor <25 % of the total mass of the liver by CT scan = use 2 GBq whole liver delivery
Tumor >25 % but <50 % of liver mass by CT scan = use 2.5 GBq whole liver delivery
Tumor >50 % of liver mass by CT scan = 3 GBq for whole liver delivery
III.
Partition Method Calculation—“Eq. 3”
![$$ {\text{Tissue}}\,{\text{Radiation}}\,{\text{Dose}}\,\left[ {\text{Gy}} \right]\,{\text{liver = }}\frac{{49670 \times {\text{Total}}\,{}^{90}{\text{Y}}\,{\text{activity}}\,{\text{in}}\,{\text{liver}}\,\left[ {\text{GBq}} \right]}}{{{\text{Mass}}\,{\text{of}}\,{\text{liver}}\,\left[ {\text{g}} \right]}} $$](/wp-content/uploads/2016/08/A174_2013_862_Chapter_Equl.gif)
4.4 Empiric Method
The first method developed for resin microspheres was clinically derived with the added data of intraoperative activity calculations (Burton et al. 1989a, b, 1990; Gray et al. 1989). There are important details regarding the differences in these patients and those now treated worldwide with resin microspheres. First, patients were previously untreated by chemotherapy or early in a course of standard 5-fluorouracil and leucovorin. Typical patients with breast, colorectal and primary cancers of the liver now have had often received multiagent chemotherapy reducing overall and liver-specific tolerance to additional anticancer therapies. Second, the volume treated included both lobes at the same time. This is not much different than current treatment approaches, which try to treat all of the tumors in each lobe with placement of microcatheters in more than one position or at the bifurcation of the right and left hepatic arteries. However, if less than the whole liver is the intent of treatment, this must be accounted for with a proportional reduction in the calculated activity planned for delivery. Third, concurrent infusion of the vasoactive agent Angiotensin II shifted microsphere deposition away from normal liver and toward irregular tumor-related neovascular arteries (Gray et al. 1989, 1990, 1992; Burton et al. 1985, 1988, 1989a, b; Van Hazel et al. 2004). Although this is potentially a useful pharmacologic strategy for broad adoption, this agent is currently only available in limited circumstances in Japan (Wu et al. 1996; Anderson et al. 1991, 1992; Goldberg et al. 1987, 1988, 1991; Archer and Gray 1989). Fourth, older resin microspheres held less activity per sphere, and therefore up to 120 million spheres were used per treatment.
It is a common finding now that if the Empiric Method is used that up to 50 % of treatments will be incomplete, i.e. not all of the microspheres can be implanted due to vascular stasis (Gulec et al. 2006b; Kennedy et al. 2006a, b). This issue is important not only from radiation safety and clean up standpoint, but also bears careful attention in the procedure not to try and deliver all the microspheres. This is not to suggest that the Empiric Method is not useful, as it can delineate the upper limit of safety in the conditions listed above in which it was developed. However in most modern-day patients, a more consistent and accurate calculation approach is the Body Surface Area method. The majority of patients will have aggregate tumor volumes between 5 and 23 %. Obviously in this wide range, individual patients cannot be optimally treated with a single activity recommendation i.e. 2 GBq.
4.5 Body Surface Area Method
Van Hazel first instituted this modification during clinical trials where radiation hepatitis appeared in patients with smaller liver volumes (Van Hazel et al. 2004). Unfortunately there has not been a subsequent publication showing the rationale, validity or correlation between BSA, liver volume, tumor volume, and radiation hepatitis. It can represent a significant decrease in activity (small patient, small liver) compared to the Empiric approach, and at other times, it calls for a modest increase in activity (small patient, large liver) compared to the Empiric Method. It has been demonstrated that the Empiric and BSA methods usually overestimate the activity that can be delivered to a patient (Kennedy et al. 2006a, b).
4.6 Partition Method
There are special situations in which a discrete lesion in the liver can be identified and the total volume of the three compartments; liver, tumor and lung, are accurately known. Using the Partition method, absorbed dose can be very accurately determined. This approach has been validated by Ho et al. (1996, 1997a, b) in a series of important papers based on human patients treated with resin microspheres. Sarfaraz concluded that using state of the art computerized radiation dose planning compared favorably to the Partition method in selected patients receiving glass microspheres (Sarfaraz et al. 2001, 2003, 2004). However, when the Partition method is misapplied and used in patients with diffuse disease it will recommend activities that would be life-threatening if delivered as shown by Kennedy et al. (2006a, b).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree