which successively shifts through an image I of size 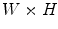 . This can be expressed as follows [13, 15]:
. This can be expressed as follows [13, 15]:
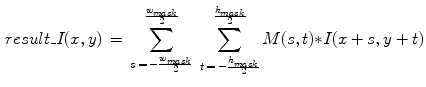
(1)
Nonlinear spatial domain filters overcome many of the linear filters’ drawbacks, and have proven their competence in elimination of impulse, uniform and fixed valued noises, without need for their explicit identification [13]. Baseline median filter implements the filtering technique expressed by Eq. (1), and is still very broadly used due to its speed and tendency to preserve the edges under certain conditions [13]. Primarily, it is applied in removal of monochromatic impulse noise with fixed noise power values (e.g. salt-and-pepper). As Eq. (1) shows, median filter like many other spatial domain filters, affects every pixel in an image, both those corrupted and uncorrupted by noise; hence, the resulting images are often blurred and have untraceable edges [13]. Many improved nonlinear spatial domain filters have been proposed in order to improve these shortcomings [13, 41]. Such filters are, for example, centre weighted median (CWM) and switching median (SM) filters which are widely implemented in removal of monochromatic impulse noise with fixed values [5, 13], and filters like adaptive CWM, adaptive SM, and progressive switching median which have been introduced for removal of random-valued monochromatic impulse noise [5, 9].
With increasing need for multichannel denoising, numerous spatial domain nonlinear filters have been proposed mostly for elimination of multichannel impulse noise [5, 26]. Early stage filters like marginal (component-wise) median filter (MMF) often applied the method of scalar filtering of each channel individually [4, 5, 16, 26]. In this way, the inherent spectral correlation between channels is ignored which commonly causes the appearance of colour artefacts in resulting images. To date, this issue has been mainly resolved using numerous vector filtering techniques which essentially consider multichannel images as vector fields, and process multichannel pixels as vectors. They have been very successfully applied in elimination of multichannel impulse noise, and can be classified into eight categories [5]:
However, basic, adaptive fuzzy, and hybrid vector filters are applied to all pixels in an image, even those not corrupted by noise; this may lead to disappearance of fine image details, blurred edges and overall excessive smoothness of resulting images [5, 13]. As a response to these issues, intelligent filters have been proposed which attempt to discern the pixels corrupted by noise from those that are not [4, 5]. Once the noisy pixels are identified, some of the vector filters (e.g. based on robust order statistics) are used; in other words, these filters switch between the identity operation and a vector filtering method, depending on some predetermined criteria. Consequently, they have reduced computational costs since a time-consuming filtering process is only executed on selected pixels observed as noisy [4, 5].
basic vector filters
adaptive fuzzy vector filters
hybrid vector filters
adaptive centre-weighted vector filters
entropy vector filters
peer group vector filters
vector sigma filters
miscellaneous (other) vector filters
In contrast to the advancement of multichannel impulse and additive denoising filters, only a small number of filtering methods (both spatial and transform domain) have been suggested so far for removal of mixed multichannel noise [9, 50, 62].
A completely novel concept of multichannel filtering based on statistical depth functions, or more precisely, statistical halfspace depth function is discussed in this chapter. Resulting halfspace deepest location filter (HSDLF) offers outstanding results in elimination of impulse and mixed multichannel noise [2, 3]. Even though HSDLF belongs to the class of spatial domain filters, its underlying algorithm is substantially different to nonlinear vector (as well as other) impulse noise filters, and transform domain filters. HSDLF filtering method is based on an adjusted version of the DEEPLOC algorithm [60] which calculates the approximate value of multivariate median (i.e. deepest location or the most central point within a data cloud) in d-dimensional space. Its multivariate/multidimensional character ensures that HSDLF intrinsically considers all channels in a multichannel image simultaneously, thus preserving the spectral correlation between channels.
HSDLF does not depend on the source and/or distribution of multichannel noise, and its efficiency in removal of:
has been verified.
multichannel (colour) impulse noise in both of its common variations: salt-and-pepper noise (with fixed values of pixel noise) and random-valued multichannel noise (with arbitrary values of pixel noise) [2], and
multichannel (colour) mixed noise, i.e. mixture of impulse (precisely, salt-and-pepper) and additive Gaussian multichannel noise (ACGN) [3],
Denoising results of HSDLF are compared in terms of objective error metrics (effectiveness) criteria and visual quality to:
marginal median multichannel filter (MMF) [16] and 25 most significant state-of-the-art multichannel impulse noise filters [1, 4, 6–8, 16–24, 27–38, 40, 43–45, 54–59, 61] for impulse multichannel noise removal
two state-of-the-art DWT based filters for removing multichannel Gaussian type noise: Probshrink [42] and BM3D (image denoising by sparse 3D transform-domain collaborative filtering) [11], as well as 26 filters for removal of multichannel impulse noise [1, 4, 6–8, 16–24, 27–38, 40, 43–45, 54–59, 61] for mixed multichannel noise removal
2 Halfspace Depth Function and Computation of Deepest Location for Multivariate Data
Finding the centre set of points within a multidimensional data cloud and generalisation of notion of median in multivariate case have been widely discussed in the literature [10, 12, 25, 39, 47–49, 53, 60, 63–65]. Since these notions cannot be directly derived from their univariate equivalents, several approaches have been introduced to address these issues with theory of statistical depth functions being the most prolific of them all. With their emerging popularity, many statistical depth functions have been formulated; Zuo and Serfling made a thorough overview and classification of all significant statistical depth functions [65]. HSDLF applies the most important representative entitled halfspace (Tukey’s or location) depth function [25, 60, 63, 65].
2.1 Definition and Properties of Halfspace Depth Function
Associated with a given probability distribution P on d-dimensional real space 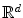 , statistical depth functions provide a P-based centre-outward ordering (and thus ranking) of points (or more precisely, Borel sets)
, statistical depth functions provide a P-based centre-outward ordering (and thus ranking) of points (or more precisely, Borel sets) 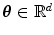 . The essential example of statistical depth functions is the halfspace (Tukey’s or location) depth function
. The essential example of statistical depth functions is the halfspace (Tukey’s or location) depth function 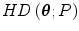 which can be defined through following equation [25, 60, 65]:
which can be defined through following equation [25, 60, 65]:
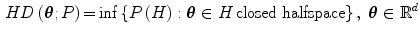
In other words, halfspace depth (HD) function denotes the minimal probability attached to any closed halfspace with 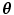 on the boundary. In a discrete case, the halfspace depth function
on the boundary. In a discrete case, the halfspace depth function 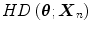 of a point
of a point 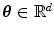 relative to a data set
relative to a data set 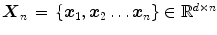 represents the smallest number of observations (elements of
represents the smallest number of observations (elements of 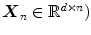 in any closed halfspace with boundary through point
in any closed halfspace with boundary through point 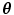 [63]. Multivariate halfspace depth can be also expressed using its univariate case
[63]. Multivariate halfspace depth can be also expressed using its univariate case 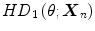 [60]:
[60]:
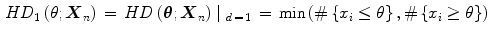
where # is a number of observations.
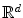 , statistical depth functions provide a P-based centre-outward ordering (and thus ranking) of points (or more precisely, Borel sets)
, statistical depth functions provide a P-based centre-outward ordering (and thus ranking) of points (or more precisely, Borel sets) 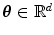 . The essential example of statistical depth functions is the halfspace (Tukey’s or location) depth function
. The essential example of statistical depth functions is the halfspace (Tukey’s or location) depth function 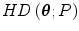 which can be defined through following equation [25, 60, 65]:
which can be defined through following equation [25, 60, 65]: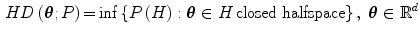
(2)
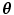 on the boundary. In a discrete case, the halfspace depth function
on the boundary. In a discrete case, the halfspace depth function 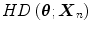 of a point
of a point 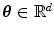 relative to a data set
relative to a data set 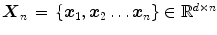 represents the smallest number of observations (elements of
represents the smallest number of observations (elements of 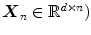 in any closed halfspace with boundary through point
in any closed halfspace with boundary through point 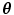 [63]. Multivariate halfspace depth can be also expressed using its univariate case
[63]. Multivariate halfspace depth can be also expressed using its univariate case 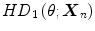 [60]:
[60]: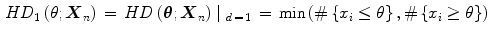
(3)
This definition interprets the halfspace depth 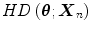 as the smallest univariate halfspace depth value of a point
as the smallest univariate halfspace depth value of a point 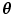 relative to any projection of the data set
relative to any projection of the data set 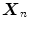 onto a direction
onto a direction 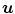 [60]:
[60]:
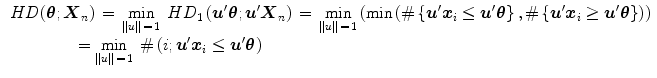
It means that halfspace depth 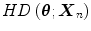 indicates how deep a point
indicates how deep a point 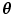 is centred within the data cloud (set). Additionally, halfspace depth is defined as multivariate ranking: points nearer the boundary of the data set have lower ranks, and the rank increases as one gets deeper inside the data cloud [60]. Ranking can be geometrically illustrated using the notion of halfspace depth regions
is centred within the data cloud (set). Additionally, halfspace depth is defined as multivariate ranking: points nearer the boundary of the data set have lower ranks, and the rank increases as one gets deeper inside the data cloud [60]. Ranking can be geometrically illustrated using the notion of halfspace depth regions 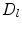 defined by equation:
defined by equation:
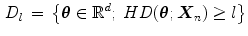
Halfspace depth regions are convex sets, and for every HD and l, 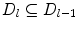 holds [60]. Boundary of a region with equivalent HD values is called halfspace depth contour. Unique centre of gravity of the smallest halfspace depth region
holds [60]. Boundary of a region with equivalent HD values is called halfspace depth contour. Unique centre of gravity of the smallest halfspace depth region 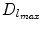 which contains the points with maximal HD values (equal to
which contains the points with maximal HD values (equal to 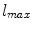 ) can be interpreted as multivariate median, i.e. a generalisation of univariate median to multidimensional spaces [60]. It also called Tukey’s median or the deepest location.
) can be interpreted as multivariate median, i.e. a generalisation of univariate median to multidimensional spaces [60]. It also called Tukey’s median or the deepest location.
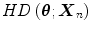 as the smallest univariate halfspace depth value of a point
as the smallest univariate halfspace depth value of a point 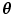 relative to any projection of the data set
relative to any projection of the data set 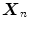 onto a direction
onto a direction 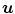 [60]:
[60]: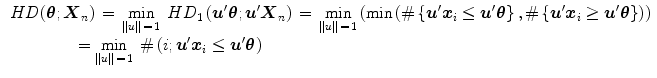
(4)
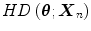 indicates how deep a point
indicates how deep a point 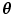 is centred within the data cloud (set). Additionally, halfspace depth is defined as multivariate ranking: points nearer the boundary of the data set have lower ranks, and the rank increases as one gets deeper inside the data cloud [60]. Ranking can be geometrically illustrated using the notion of halfspace depth regions
is centred within the data cloud (set). Additionally, halfspace depth is defined as multivariate ranking: points nearer the boundary of the data set have lower ranks, and the rank increases as one gets deeper inside the data cloud [60]. Ranking can be geometrically illustrated using the notion of halfspace depth regions 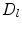 defined by equation:
defined by equation: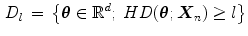
(5)
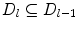 holds [60]. Boundary of a region with equivalent HD values is called halfspace depth contour. Unique centre of gravity of the smallest halfspace depth region
holds [60]. Boundary of a region with equivalent HD values is called halfspace depth contour. Unique centre of gravity of the smallest halfspace depth region 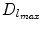 which contains the points with maximal HD values (equal to
which contains the points with maximal HD values (equal to 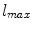 ) can be interpreted as multivariate median, i.e. a generalisation of univariate median to multidimensional spaces [60]. It also called Tukey’s median or the deepest location.
) can be interpreted as multivariate median, i.e. a generalisation of univariate median to multidimensional spaces [60]. It also called Tukey’s median or the deepest location.Zuo and Serfling have shown that halfspace depth function 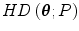 fulfils all useful and desirable properties required of a statistical depth function [65]:
fulfils all useful and desirable properties required of a statistical depth function [65]:
Affine invariance is a particularly useful property for calculation of deepest location; in case of HD, this means that for any affine transformation 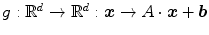 , with
, with 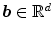 and
and 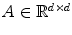 a nonsingular matrix, equality
a nonsingular matrix, equality 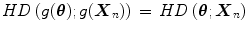 holds. Consequently, the deepest location (Tukey’s median)
holds. Consequently, the deepest location (Tukey’s median) 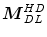 is also affine equivariant:
is also affine equivariant: 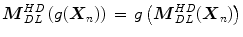 .
.
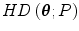 fulfils all useful and desirable properties required of a statistical depth function [65]:
fulfils all useful and desirable properties required of a statistical depth function [65]:
Affine invariance.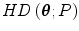 is independent of the coordinate system.
is independent of the coordinate system.
Maximality at center. If P is symmetric about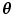 in some sense, then
in some sense, then 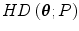 is maximal at this point.
is maximal at this point.
Symmetry. If P is symmetric about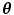 in some sense, then so is
in some sense, then so is 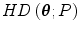 .
.
Decreasing along rays. The depth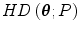 decreases along every ray from the deepest point.
decreases along every ray from the deepest point.
Vanishing at infinity.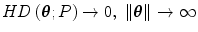 .
.
Continuity of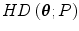 as a function of
as a function of 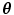 (upper semicontinuity).
(upper semicontinuity).
Continuity as of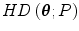 a functional of P.
a functional of P.
Quasi-concavity as a function of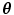 . The set
. The set 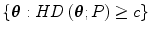 is convex for each real c.
is convex for each real c.
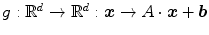 , with
, with 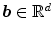 and
and 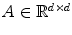 a nonsingular matrix, equality
a nonsingular matrix, equality 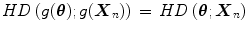 holds. Consequently, the deepest location (Tukey’s median)
holds. Consequently, the deepest location (Tukey’s median) 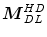 is also affine equivariant:
is also affine equivariant: 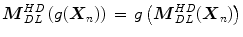 .
.Furthermore, Tukey’s median is a very robust multivariate location estimator, and its robustness can be evaluated by means of the breakdown value 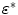 . As proven by Donoho and Gasko [12], Tukey’s median
. As proven by Donoho and Gasko [12], Tukey’s median 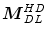 satisfies the inequality
satisfies the inequality 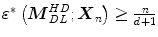 for any sample in general position. This means that the resulting Tukey’s median
for any sample in general position. This means that the resulting Tukey’s median 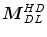 will not move outside of a bounded region if
will not move outside of a bounded region if 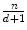 observations are replaced from the data set
observations are replaced from the data set 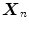 . If the original data set
. If the original data set 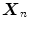 comes from any angularly symmetric distribution, and especially from an elliptically symmetric distribution, the breakdown value
comes from any angularly symmetric distribution, and especially from an elliptically symmetric distribution, the breakdown value 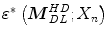 tends to
tends to 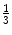 in any dimension. Simply put, if at least 67 % of the data points in
in any dimension. Simply put, if at least 67 % of the data points in 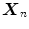 are drawn from such a distribution then the deepest location remains within reasonable limits, regardless of the other points in the data set.
are drawn from such a distribution then the deepest location remains within reasonable limits, regardless of the other points in the data set.
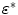 . As proven by Donoho and Gasko [12], Tukey’s median
. As proven by Donoho and Gasko [12], Tukey’s median 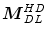 satisfies the inequality
satisfies the inequality 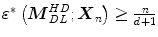 for any sample in general position. This means that the resulting Tukey’s median
for any sample in general position. This means that the resulting Tukey’s median 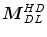 will not move outside of a bounded region if
will not move outside of a bounded region if 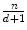 observations are replaced from the data set
observations are replaced from the data set 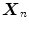 . If the original data set
. If the original data set 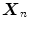 comes from any angularly symmetric distribution, and especially from an elliptically symmetric distribution, the breakdown value
comes from any angularly symmetric distribution, and especially from an elliptically symmetric distribution, the breakdown value 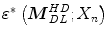 tends to
tends to 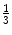 in any dimension. Simply put, if at least 67 % of the data points in
in any dimension. Simply put, if at least 67 % of the data points in 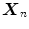 are drawn from such a distribution then the deepest location remains within reasonable limits, regardless of the other points in the data set.
are drawn from such a distribution then the deepest location remains within reasonable limits, regardless of the other points in the data set.In general, not many algorithms have been proposed for calculation of statistical depth functions. A number of algorithms for computation of halfspace depth have been proposed in the literature [10, 47–49, 60, 64]; however, only a few algorithms for finding multivariate halfspace deepest location (Tukey’s median) have been proposed: [48] for bivariate data, and, [10, 47] and [60] for dimensions more than two. DEEPLOC algorithm [60] has been selected as a basis of HSDLF, primarily because it implements the only mathematically proven and exact algorithm for calculation of halfspace depth functions in 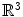 [49, 60]. Most importantly, it has been shown that approximate location depth calculated with DEEPLOC is very close to the exact depth for real data sets [60].
[49, 60]. Most importantly, it has been shown that approximate location depth calculated with DEEPLOC is very close to the exact depth for real data sets [60].
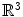 [49, 60]. Most importantly, it has been shown that approximate location depth calculated with DEEPLOC is very close to the exact depth for real data sets [60].
[49, 60]. Most importantly, it has been shown that approximate location depth calculated with DEEPLOC is very close to the exact depth for real data sets [60].2.2 Finding the Deepest Location Using DEEPLOC Algorithm
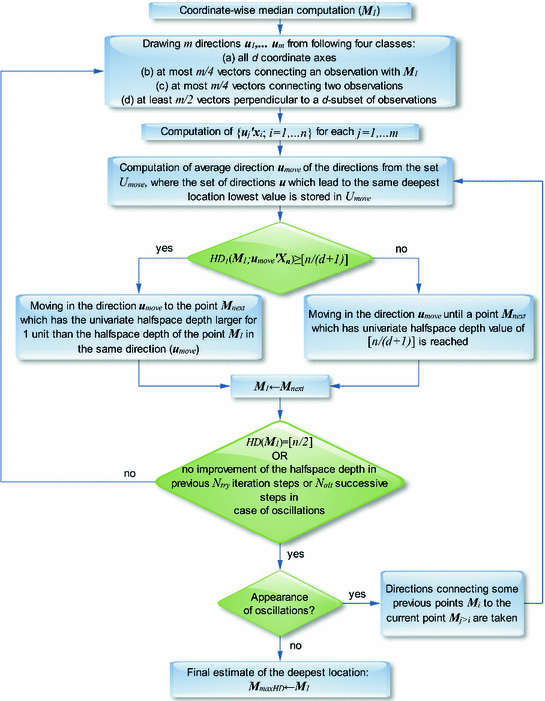
DEEPLOC algorithm computes an approximation of deepest location (Tukey’s median) for any dimension d. It works with a subset of directions u [see Eq. (4)] to approximate the halfspace depth, and is constructed to be the least time consuming [49, 60]. DEEPLOC algorithm and its stepwise pseudocode are presented in their full (and complex) details in the original work of Struyf and Rousseeuw [60]. In this section only the most significant steps in DEEPLOC are explained which are of importance for understanding of how HSDLF works. Also, the places where the original DEEPLOC algorithm is altered are indicated.
In short, DEEPLOC starts from an initial point and takes further steps in carefully selected directions in which the halfspace depth can be increased (unlike the solution proposed in [10]), so that the deepest location (Tukey’s median) can be approached after several of these steps. In order to reduce the number of steps, a centrally located initial point like coordinate-wise median or (affine invariant) coordinate-wise mean is taken, since it gives a fairly good halfspace depth relative to the data set, and is easy to compute [60]:
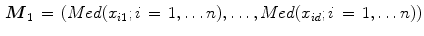
After calculating the starting point, m directions 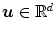 are constructed with
are constructed with 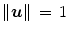 . These directions are randomly drawn from following classes [60]:
. These directions are randomly drawn from following classes [60]:
Classes (a), (b) and (c) are included as they are easy to compute, and are used for detection of marginal and far outliers [60]. However, class (d) directions are of greatest importance due to their close relation to halfspace depth notion, thus the majority of directions are taken from it. As a basis, HSDLF uses the proportion of directions from the original DEEPLOC algorithm [60]:
However, an additional parameter which controls the distribution of directions is introduced in HSDLF, and is called threshold control parameter (see Sect. 3). The overall number of directions m can be given by the user and in case of HSDLF, m = 500 directions are computed by default (see Sect. 3).
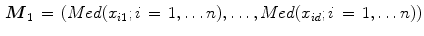
(6)
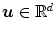 are constructed with
are constructed with 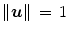 . These directions are randomly drawn from following classes [60]:
. These directions are randomly drawn from following classes [60]:(a)
d coordinate axes
(b)
vectors connecting an observation with 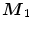
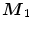
(c)
vectors connecting two observations
(d)
vectors perpendicular to a d-subset of observations
all directions from the class (a)
at most m/4 directions from each of the classes (b) and (c)
at least m/2 directions from the class (d)
Univariate halfspace depth of 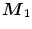 relative to the projection of
relative to the projection of 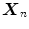 on each of these m directions is then computed. The directions u which lead to the same lowest value
on each of these m directions is then computed. The directions u which lead to the same lowest value 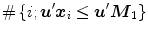 are stored in set
are stored in set  , and these directions are considered as the ones in which the halfspace depth is able to improve [60]. The average direction
, and these directions are considered as the ones in which the halfspace depth is able to improve [60]. The average direction  of directions saved in set
of directions saved in set 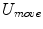 is then calculated:
is then calculated:
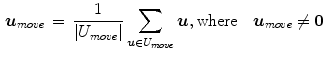
After that, a step is taken from 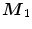 in the direction of
in the direction of 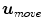 . As mentioned, the value of halfspace depth at the deepest location relative to
. As mentioned, the value of halfspace depth at the deepest location relative to 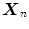 has to be at least
has to be at least ![$$\left[ {\frac{n}{d+1}} \right] $$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq65.gif) (where square brackets represent the floor function). If this condition is not fulfilled for
(where square brackets represent the floor function). If this condition is not fulfilled for 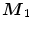 , i.e. if following inequality holds:
, i.e. if following inequality holds:
![$$\begin{aligned} H D_1 \left( {{\varvec{M}}_1 ;{\varvec{u}}'_{move} {\varvec{X}}_n} \right) <\left[ {\frac{n}{d+1}} \right] \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_Equ8.gif)
a step in the direction 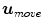 is taken, which is large enough to reach a point
is taken, which is large enough to reach a point 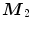 which has univariate halfspace depth value of
which has univariate halfspace depth value of ![$$\left[ {\frac{n}{d+1}} \right] $$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq69.gif) . Otherwise, a step is taken in the direction
. Otherwise, a step is taken in the direction 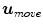 to the point
to the point 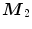 which has univariate halfspace depth larger for 1 unit than the halfspace depth of
which has univariate halfspace depth larger for 1 unit than the halfspace depth of 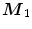 in the same direction
in the same direction 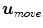 [60].
[60].
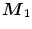 relative to the projection of
relative to the projection of 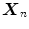 on each of these m directions is then computed. The directions u which lead to the same lowest value
on each of these m directions is then computed. The directions u which lead to the same lowest value 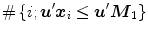 are stored in set
are stored in set 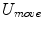 , and these directions are considered as the ones in which the halfspace depth is able to improve [60]. The average direction
, and these directions are considered as the ones in which the halfspace depth is able to improve [60]. The average direction 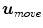 of directions saved in set
of directions saved in set 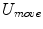 is then calculated:
is then calculated: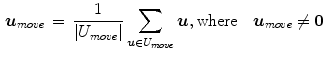
(7)
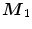 in the direction of
in the direction of 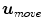 . As mentioned, the value of halfspace depth at the deepest location relative to
. As mentioned, the value of halfspace depth at the deepest location relative to 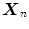 has to be at least
has to be at least ![$$\left[ {\frac{n}{d+1}} \right] $$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq65.gif) (where square brackets represent the floor function). If this condition is not fulfilled for
(where square brackets represent the floor function). If this condition is not fulfilled for 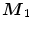 , i.e. if following inequality holds:
, i.e. if following inequality holds:![$$\begin{aligned} H D_1 \left( {{\varvec{M}}_1 ;{\varvec{u}}'_{move} {\varvec{X}}_n} \right) <\left[ {\frac{n}{d+1}} \right] \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_Equ8.gif)
(8)
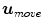 is taken, which is large enough to reach a point
is taken, which is large enough to reach a point 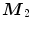 which has univariate halfspace depth value of
which has univariate halfspace depth value of ![$$\left[ {\frac{n}{d+1}} \right] $$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq69.gif) . Otherwise, a step is taken in the direction
. Otherwise, a step is taken in the direction 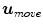 to the point
to the point 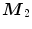 which has univariate halfspace depth larger for 1 unit than the halfspace depth of
which has univariate halfspace depth larger for 1 unit than the halfspace depth of 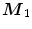 in the same direction
in the same direction 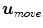 [60].
[60].Afterwards, the explained procedure is repeated with 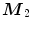 (or
(or 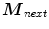 in iteration for next
in iteration for next ![$$>$$” src=”/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq76.gif”></SPAN>2) taking the roll of the initial point (<SPAN id=IEq77 class=InlineEquation><IMG alt=$${\varvec{M}}_{1}$$ src=]() in previously described algorithm steps) until a point
in previously described algorithm steps) until a point 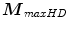 is found with maximal halfspace depth of
is found with maximal halfspace depth of 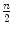 , or until the algorithm stops showing any halfspace depth improvement in previous
, or until the algorithm stops showing any halfspace depth improvement in previous 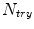 iteration steps. If the algorithm begins to oscillate instead of moving towards the deepest location, supplemental features are proposed for reduction of computational cost: if no halfspace depth improvement has been made after
iteration steps. If the algorithm begins to oscillate instead of moving towards the deepest location, supplemental features are proposed for reduction of computational cost: if no halfspace depth improvement has been made after 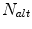 successive steps, then the directions connecting some previous points
successive steps, then the directions connecting some previous points 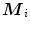 to the current point
to the current point ![$${\varvec{M}}_{j>i}$$” src=”/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq83.gif”></SPAN> are considered [<CITE><A href=]() 60]. It should be noted that parameters
60]. It should be noted that parameters  and
and  are also user defined.
are also user defined.
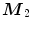 (or
(or 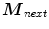 in iteration for next
in iteration for next 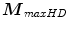 is found with maximal halfspace depth of
is found with maximal halfspace depth of 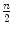 , or until the algorithm stops showing any halfspace depth improvement in previous
, or until the algorithm stops showing any halfspace depth improvement in previous 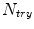 iteration steps. If the algorithm begins to oscillate instead of moving towards the deepest location, supplemental features are proposed for reduction of computational cost: if no halfspace depth improvement has been made after
iteration steps. If the algorithm begins to oscillate instead of moving towards the deepest location, supplemental features are proposed for reduction of computational cost: if no halfspace depth improvement has been made after 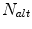 successive steps, then the directions connecting some previous points
successive steps, then the directions connecting some previous points 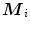 to the current point
to the current point 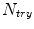 and
and 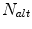 are also user defined.
are also user defined.
Fig. 1
Flowchart illustrating the most significant steps of the DEEPLOC algorithm
3 Halfspace Deepest Location Filter
DEEPLOC pseudocode served as a foundation of the HSDLF’s programming code [2, 3]. During the experiments (see Sect. 4), it has been empirically established that a slight increase in number of directions from class (d) (defined in Sect. 2.2) improves filtering results. In order to give HSDLF an additional degree of freedom and even more flexibility, a scalar parameter entitled threshold control parameter 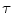 was introduced with values ranging from 0 to 1, which controls the percentage of class (d) directions1. As directions from class (d) play the vital role in DEEPLOC algorithm, parameter
was introduced with values ranging from 0 to 1, which controls the percentage of class (d) directions1. As directions from class (d) play the vital role in DEEPLOC algorithm, parameter 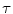 aims to provide fine-tuning of HSDLF’s output results and precision. Experiments have shown that this small increase in number of class (d) directions has an insignificant impact on computational cost [2, 3].
aims to provide fine-tuning of HSDLF’s output results and precision. Experiments have shown that this small increase in number of class (d) directions has an insignificant impact on computational cost [2, 3].
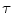 was introduced with values ranging from 0 to 1, which controls the percentage of class (d) directions1. As directions from class (d) play the vital role in DEEPLOC algorithm, parameter
was introduced with values ranging from 0 to 1, which controls the percentage of class (d) directions1. As directions from class (d) play the vital role in DEEPLOC algorithm, parameter 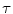 aims to provide fine-tuning of HSDLF’s output results and precision. Experiments have shown that this small increase in number of class (d) directions has an insignificant impact on computational cost [2, 3].
aims to provide fine-tuning of HSDLF’s output results and precision. Experiments have shown that this small increase in number of class (d) directions has an insignificant impact on computational cost [2, 3].HSDLF applies this adjusted version of the DEEPLOC algorithm for calculating deepest location (Tukey’s median) in three dimensional space (d = 3 in notation of Sects. 2.1 and 2.2), where R, G and B colour channels act as dimensions (coordinates). It was assumed that the multichannel images are 24-bit (8-bit per channel), so the values of R, G and B channels range from 0 to 255 for each channel.
HSDLF uses the standard spatial filtering technique based on a sliding convolution kernel (filtering window) described in Sect. 2 [2, 3]. Let 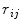 ,
, 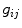 , and
, and 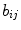 denote the values of red, green, and blue channels, respectively, of a pixel at the position (i,j) in an image I of size
denote the values of red, green, and blue channels, respectively, of a pixel at the position (i,j) in an image I of size 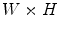 contaminated by multichannel noise, i.e.
contaminated by multichannel noise, i.e. 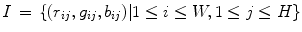 . Convolution kernel M of size
. Convolution kernel M of size 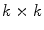 , where k is an odd positive integer, includes the pixel positioned at the centre of kernel M, i.e. (i,j) in the image I, and
, where k is an odd positive integer, includes the pixel positioned at the centre of kernel M, i.e. (i,j) in the image I, and 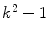 of its neighbouring pixels. This means that the kernel M enfolds
of its neighbouring pixels. This means that the kernel M enfolds 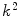 ordered triplets of red, green and blue channel values, respectively, of corresponding pixels. HSDLF computes the deepest location within a data cloud which consists of these
ordered triplets of red, green and blue channel values, respectively, of corresponding pixels. HSDLF computes the deepest location within a data cloud which consists of these 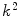 three dimensional data using the adjusted DEEPLOC algorithm, and replaces the channel values of pixel at the centre of kernel M ((i,j) in image I) with estimated deepest location’s channel values. Image edges are handled identically as in standard (marginal) median filters.
three dimensional data using the adjusted DEEPLOC algorithm, and replaces the channel values of pixel at the centre of kernel M ((i,j) in image I) with estimated deepest location’s channel values. Image edges are handled identically as in standard (marginal) median filters.
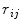 ,
, 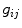 , and
, and 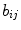 denote the values of red, green, and blue channels, respectively, of a pixel at the position (i,j) in an image I of size
denote the values of red, green, and blue channels, respectively, of a pixel at the position (i,j) in an image I of size 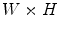 contaminated by multichannel noise, i.e.
contaminated by multichannel noise, i.e. 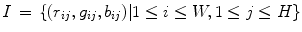 . Convolution kernel M of size
. Convolution kernel M of size 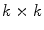 , where k is an odd positive integer, includes the pixel positioned at the centre of kernel M, i.e. (i,j) in the image I, and
, where k is an odd positive integer, includes the pixel positioned at the centre of kernel M, i.e. (i,j) in the image I, and 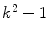 of its neighbouring pixels. This means that the kernel M enfolds
of its neighbouring pixels. This means that the kernel M enfolds 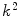 ordered triplets of red, green and blue channel values, respectively, of corresponding pixels. HSDLF computes the deepest location within a data cloud which consists of these
ordered triplets of red, green and blue channel values, respectively, of corresponding pixels. HSDLF computes the deepest location within a data cloud which consists of these 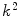 three dimensional data using the adjusted DEEPLOC algorithm, and replaces the channel values of pixel at the centre of kernel M ((i,j) in image I) with estimated deepest location’s channel values. Image edges are handled identically as in standard (marginal) median filters.
three dimensional data using the adjusted DEEPLOC algorithm, and replaces the channel values of pixel at the centre of kernel M ((i,j) in image I) with estimated deepest location’s channel values. Image edges are handled identically as in standard (marginal) median filters.Number of directions is kept at a fixed value of m = 500 since this is the minimum value of m for which HSDLF gives excellent balance between high performance and computation time. It was shown that the algorithm accuracy gradually increases with an increase in number of directions m; however, the computational cost grows rapidly [2, 3].
In early stages of HSDLF testing on 24-bit multichannel images, it was noted that deepest location channel values in very rare cases with far outliers can be negative (precisely, take value 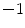 ), or can exceed the limit of 255 (precisely, take value of 256). In order to preserve the visual smoothness and consistency of filtered images without affecting the computational cost, these particular pixels are additionally filtered with MMF [5], which is very fast and calculated analogously to HSDLF. This correction would not be needed if the number of directions m was set to value of more than 1,500 or if another colour system such as CIELab or YCbCr was used. However, in the latter case, a different range of channel values in these colour systems sometimes causes difficulties in calculation of location depth/deepest location.
), or can exceed the limit of 255 (precisely, take value of 256). In order to preserve the visual smoothness and consistency of filtered images without affecting the computational cost, these particular pixels are additionally filtered with MMF [5], which is very fast and calculated analogously to HSDLF. This correction would not be needed if the number of directions m was set to value of more than 1,500 or if another colour system such as CIELab or YCbCr was used. However, in the latter case, a different range of channel values in these colour systems sometimes causes difficulties in calculation of location depth/deepest location.

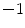 ), or can exceed the limit of 255 (precisely, take value of 256). In order to preserve the visual smoothness and consistency of filtered images without affecting the computational cost, these particular pixels are additionally filtered with MMF [5], which is very fast and calculated analogously to HSDLF. This correction would not be needed if the number of directions m was set to value of more than 1,500 or if another colour system such as CIELab or YCbCr was used. However, in the latter case, a different range of channel values in these colour systems sometimes causes difficulties in calculation of location depth/deepest location.
), or can exceed the limit of 255 (precisely, take value of 256). In order to preserve the visual smoothness and consistency of filtered images without affecting the computational cost, these particular pixels are additionally filtered with MMF [5], which is very fast and calculated analogously to HSDLF. This correction would not be needed if the number of directions m was set to value of more than 1,500 or if another colour system such as CIELab or YCbCr was used. However, in the latter case, a different range of channel values in these colour systems sometimes causes difficulties in calculation of location depth/deepest location.
Fig. 2
Benchmark images used for comparison of all observed filters’ denoising performances, from left to right (image dimensions in pixels are given in brackets): Caps (768 512), Couple (256
512), Couple (256 256), F16 (512
256), F16 (512 512), Girl1 (256
512), Girl1 (256 256), Girl2 (256
256), Girl2 (256 256), Girl3 (256
256), Girl3 (256 256), House (256
256), House (256 256), House With Car (512
256), House With Car (512 512), Jellybeans1 (256
512), Jellybeans1 (256 256), Jellybeans2 (256
256), Jellybeans2 (256 256), Lena (512
256), Lena (512 512), Mandrill (512
512), Mandrill (512 512), Parrots (768
512), Parrots (768 512), Peppers (512
512), Peppers (512 512), Sailboat (512
512), Sailboat (512 512), Splash (512
512), Splash (512 512), Tiffany (512
512), Tiffany (512 512), and Tree (256
512), and Tree (256 256)
256)
 512), Couple (256
512), Couple (256 256), F16 (512
256), F16 (512 512), Girl1 (256
512), Girl1 (256 256), Girl2 (256
256), Girl2 (256 256), Girl3 (256
256), Girl3 (256 256), House (256
256), House (256 256), House With Car (512
256), House With Car (512 512), Jellybeans1 (256
512), Jellybeans1 (256 256), Jellybeans2 (256
256), Jellybeans2 (256 256), Lena (512
256), Lena (512 512), Mandrill (512
512), Mandrill (512 512), Parrots (768
512), Parrots (768 512), Peppers (512
512), Peppers (512 512), Sailboat (512
512), Sailboat (512 512), Splash (512
512), Splash (512 512), Tiffany (512
512), Tiffany (512 512), and Tree (256
512), and Tree (256 256)
256)It is important to point out that in case of the image set used in Sect. 4 for all observed types and/or powers of multichannel noise, and observed values of threshold control parameter 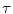 , the filtering results with and without this MMF correction are identical, and no cases of deepest location values going out of
, the filtering results with and without this MMF correction are identical, and no cases of deepest location values going out of ![$$\left[ {0,255} \right] $$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq117.gif) range appear on this image data set, even though the number of directions m is set to 500 [2, 3]. Also, HSDLF evidently does not depend on the nature or powers of applied multichannel noise; therefore, it can be used for elimination of many types of multichannel noise regardless of their origin [2, 3].
range appear on this image data set, even though the number of directions m is set to 500 [2, 3]. Also, HSDLF evidently does not depend on the nature or powers of applied multichannel noise; therefore, it can be used for elimination of many types of multichannel noise regardless of their origin [2, 3].
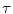 , the filtering results with and without this MMF correction are identical, and no cases of deepest location values going out of
, the filtering results with and without this MMF correction are identical, and no cases of deepest location values going out of ![$$\left[ {0,255} \right] $$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_IEq117.gif) range appear on this image data set, even though the number of directions m is set to 500 [2, 3]. Also, HSDLF evidently does not depend on the nature or powers of applied multichannel noise; therefore, it can be used for elimination of many types of multichannel noise regardless of their origin [2, 3].
range appear on this image data set, even though the number of directions m is set to 500 [2, 3]. Also, HSDLF evidently does not depend on the nature or powers of applied multichannel noise; therefore, it can be used for elimination of many types of multichannel noise regardless of their origin [2, 3].4 Experimental Results and Their Analysis
Performance of HSDLF has been tested on some of the most commonly used 24-bit multichannel (8-bit per colour channel) benchmark images: Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous image database set, with addition of two more images (“Parrots” and “Caps”) from the Kodak Photo CD PCD0992 [2, 3]. These 24-bit (i.e. 8-bit-per-channel) multichannel benchmark images have fixed image sizes of 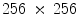 pixels (“Couple”, “Girl1”, “Girl2”, “Girl3”, “House”, “Jellybeans1”, “Jellybeans2”, “Tree”),
pixels (“Couple”, “Girl1”, “Girl2”, “Girl3”, “House”, “Jellybeans1”, “Jellybeans2”, “Tree”), 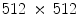 pixels (“F16”, “House With Car”, “Lena”, “Mandrill”, “Peppers”, “Sailboat”, “Splash”, “Tiffany”) and
pixels (“F16”, “House With Car”, “Lena”, “Mandrill”, “Peppers”, “Sailboat”, “Splash”, “Tiffany”) and  pixels (“Caps”, “Parrots”) (see Fig. 2).
pixels (“Caps”, “Parrots”) (see Fig. 2).
 pixels (“Couple”, “Girl1”, “Girl2”, “Girl3”, “House”, “Jellybeans1”, “Jellybeans2”, “Tree”),
pixels (“Couple”, “Girl1”, “Girl2”, “Girl3”, “House”, “Jellybeans1”, “Jellybeans2”, “Tree”),  pixels (“F16”, “House With Car”, “Lena”, “Mandrill”, “Peppers”, “Sailboat”, “Splash”, “Tiffany”) and
pixels (“F16”, “House With Car”, “Lena”, “Mandrill”, “Peppers”, “Sailboat”, “Splash”, “Tiffany”) and  pixels (“Caps”, “Parrots”) (see Fig. 2).
pixels (“Caps”, “Parrots”) (see Fig. 2).However, due to very large amount of data, comparison of HSDLF’s performance against 28 state-of-the-art filters will be presented for four essential benchmark images, namely “Lena” and “Peppers” (with sizes of 512 512 pixels) from Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous image database, and “Parrots” and “Caps” (with sizes of 768
512 pixels) from Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous image database, and “Parrots” and “Caps” (with sizes of 768 512 pixels) from Kodak Photo CD PCD0992.
512 pixels) from Kodak Photo CD PCD0992.
 512 pixels) from Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous image database, and “Parrots” and “Caps” (with sizes of 768
512 pixels) from Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous image database, and “Parrots” and “Caps” (with sizes of 768 512 pixels) from Kodak Photo CD PCD0992.
512 pixels) from Kodak Photo CD PCD0992.In all experiments, the convolution kernel (sliding filtering window) size is set to 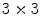 (see Sect. 3). HSDLF results have been produced using Simple DirectMedia Layer and CImg open source libraries within C++ programming language framework. Consequently, HSDLF does not require any specific digital image format, and can be successfully applied to nearly all digital image formats, including lossy compressed formats like JPEG. All types of noise have been generated using MATLAB R2011a software.
(see Sect. 3). HSDLF results have been produced using Simple DirectMedia Layer and CImg open source libraries within C++ programming language framework. Consequently, HSDLF does not require any specific digital image format, and can be successfully applied to nearly all digital image formats, including lossy compressed formats like JPEG. All types of noise have been generated using MATLAB R2011a software.
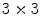 (see Sect. 3). HSDLF results have been produced using Simple DirectMedia Layer and CImg open source libraries within C++ programming language framework. Consequently, HSDLF does not require any specific digital image format, and can be successfully applied to nearly all digital image formats, including lossy compressed formats like JPEG. All types of noise have been generated using MATLAB R2011a software.
(see Sect. 3). HSDLF results have been produced using Simple DirectMedia Layer and CImg open source libraries within C++ programming language framework. Consequently, HSDLF does not require any specific digital image format, and can be successfully applied to nearly all digital image formats, including lossy compressed formats like JPEG. All types of noise have been generated using MATLAB R2011a software.4.1 Multichannel Impulse Noise Removal
As mentioned in Sect. 1, performances of HSDLF and other multichannel impulse noise filters are compared on images corrupted by salt-and-pepper as well as random-valued noise, with following power levels/densities applied: 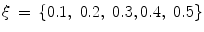 .
.
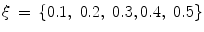 .
.Salt-and-pepper noise on image I is generated using MATLAB built-in 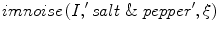 function where
function where 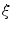 denotes the noise density. This means that approximately
denotes the noise density. This means that approximately 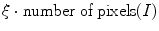 randomly chosen pixels are replaced by pixels which have values of 0 or 255 on each channel (red, green and blue). Random-valued noise with density
randomly chosen pixels are replaced by pixels which have values of 0 or 255 on each channel (red, green and blue). Random-valued noise with density 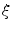 on image I is generated indirectly since MATLAB does not have a built-in function for its production. Using the built-in MATLAB function
on image I is generated indirectly since MATLAB does not have a built-in function for its production. Using the built-in MATLAB function 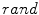 for generation of uniformly distributed pseudorandom numbers,
for generation of uniformly distributed pseudorandom numbers, 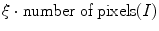 pixels are selected randomly and then replaced by pixels with random values ranging from 0 to 255 on each colour channel (red, green and blue). Obviously, salt-and-pepper noise could be produced similarly using MATLAB function
pixels are selected randomly and then replaced by pixels with random values ranging from 0 to 255 on each colour channel (red, green and blue). Obviously, salt-and-pepper noise could be produced similarly using MATLAB function 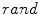 ; experiments have shown that both of these methods for generating salt-and-pepper noise give identical results [2]. Salt-and-pepper and random-valued noise can be considered as instances of uncorrelated impulsive noise model [5]:
; experiments have shown that both of these methods for generating salt-and-pepper noise give identical results [2]. Salt-and-pepper and random-valued noise can be considered as instances of uncorrelated impulsive noise model [5]:
![$$\begin{aligned} \begin{array}{l} c_{ij}^{(ch)} \,=\,\left\{ {{\begin{array}{l} {r_{ij}^{(ch)} \;\text {with probability }\xi } \\ {o_{ij}^{(ch)} \;\text {with probability 1-}\xi } \\ \end{array} }} \right. \\ \\ r_{ij}^{(ch)} \in \left\{ {{ \begin{array}{l} {\left\{ {0,255} \right\} \;\text {for salt-and-pepper noise}} \\ {\left[ {0,255} \right] \;\text {for random-valued noise}} \\ \end{array} }} \right. \\ \end{array} \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_Equ9.gif)
where 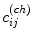 represents the pixel channel value (red, green or blue) of the output image corrupted by noise,
represents the pixel channel value (red, green or blue) of the output image corrupted by noise, 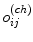 represents the pixel channel value (red, green or blue) of the original image uncorrupted by noise, and
represents the pixel channel value (red, green or blue) of the original image uncorrupted by noise, and 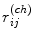 represents the pixel channel value (red, green or blue) of salt-and-pepper or random-valued noise; ch denotes the colour channel index: ch = 1 for red, ch = 2 green, and ch = 3 blue channel, and
represents the pixel channel value (red, green or blue) of salt-and-pepper or random-valued noise; ch denotes the colour channel index: ch = 1 for red, ch = 2 green, and ch = 3 blue channel, and 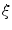 symbolises the density of impulse noise that is applied to an image.
symbolises the density of impulse noise that is applied to an image.
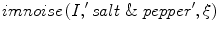 function where
function where 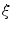 denotes the noise density. This means that approximately
denotes the noise density. This means that approximately 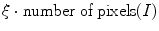 randomly chosen pixels are replaced by pixels which have values of 0 or 255 on each channel (red, green and blue). Random-valued noise with density
randomly chosen pixels are replaced by pixels which have values of 0 or 255 on each channel (red, green and blue). Random-valued noise with density 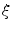 on image I is generated indirectly since MATLAB does not have a built-in function for its production. Using the built-in MATLAB function
on image I is generated indirectly since MATLAB does not have a built-in function for its production. Using the built-in MATLAB function  for generation of uniformly distributed pseudorandom numbers,
for generation of uniformly distributed pseudorandom numbers, 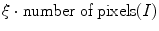 pixels are selected randomly and then replaced by pixels with random values ranging from 0 to 255 on each colour channel (red, green and blue). Obviously, salt-and-pepper noise could be produced similarly using MATLAB function
pixels are selected randomly and then replaced by pixels with random values ranging from 0 to 255 on each colour channel (red, green and blue). Obviously, salt-and-pepper noise could be produced similarly using MATLAB function 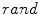 ; experiments have shown that both of these methods for generating salt-and-pepper noise give identical results [2]. Salt-and-pepper and random-valued noise can be considered as instances of uncorrelated impulsive noise model [5]:
; experiments have shown that both of these methods for generating salt-and-pepper noise give identical results [2]. Salt-and-pepper and random-valued noise can be considered as instances of uncorrelated impulsive noise model [5]:![$$\begin{aligned} \begin{array}{l} c_{ij}^{(ch)} \,=\,\left\{ {{\begin{array}{l} {r_{ij}^{(ch)} \;\text {with probability }\xi } \\ {o_{ij}^{(ch)} \;\text {with probability 1-}\xi } \\ \end{array} }} \right. \\ \\ r_{ij}^{(ch)} \in \left\{ {{ \begin{array}{l} {\left\{ {0,255} \right\} \;\text {for salt-and-pepper noise}} \\ {\left[ {0,255} \right] \;\text {for random-valued noise}} \\ \end{array} }} \right. \\ \end{array} \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_5_Chapter_Equ9.gif)
(9)
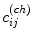 represents the pixel channel value (red, green or blue) of the output image corrupted by noise,
represents the pixel channel value (red, green or blue) of the output image corrupted by noise, 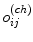 represents the pixel channel value (red, green or blue) of the original image uncorrupted by noise, and
represents the pixel channel value (red, green or blue) of the original image uncorrupted by noise, and 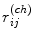 represents the pixel channel value (red, green or blue) of salt-and-pepper or random-valued noise; ch denotes the colour channel index: ch = 1 for red, ch = 2 green, and ch = 3 blue channel, and
represents the pixel channel value (red, green or blue) of salt-and-pepper or random-valued noise; ch denotes the colour channel index: ch = 1 for red, ch = 2 green, and ch = 3 blue channel, and 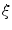 symbolises the density of impulse noise that is applied to an image.
symbolises the density of impulse noise that is applied to an image.HSDLF performance in removal of multichannel impulse noise is compared to marginal median filter MMF [4] and following 25 state-of-the-art impulse noise filters [2, 5]:
Filtering results are compared objectively by means of three error metrics criteria [5]:
Experimental results have shown that HSDLF provides optimal results in removal of multichannel impulse noise for two values of threshold control parameter 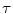 (0.0015 and 0.005) in terms of both objective error metrics criteria and visual quality [2]. Tested on Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous and Kodak Photo CD PCD0992 image data sets, it has also been verified that HSDLF performances in multichannel impulse denoising deteriorate quickly for
(0.0015 and 0.005) in terms of both objective error metrics criteria and visual quality [2]. Tested on Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous and Kodak Photo CD PCD0992 image data sets, it has also been verified that HSDLF performances in multichannel impulse denoising deteriorate quickly for 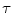
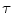
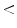 0.0012.
0.0012.
adaptive basic vector directional filter ABVDF [29]
adaptive multichannel nonparametric filter with multivariate exponential kernel function AMNFE [43]
adaptive vector median filter AVMF [28]
basic vector directional filter BVDF [61]
fast peer group filter FPGF [54]
peer group filter PGF [18]
robust switching vector median filter RSVMF [4]
vector median filter VMF [1]
vector signal-dependent rank order mean filter VSDROMF [40]
peak signal-to-noise ratio (PSNR) in decibels (dB) which measures the noise suppression capability of a filter:
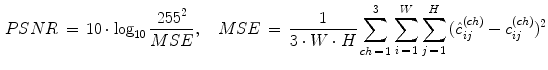
(10)
mean absolute error (MAE) which measures the detail preservation capability of a filter:
where in Eqs. (10) and (11),
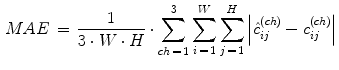
(11)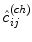 and
and 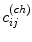 represent the pixel channel values of denoised and original images, respectively, and ch symbolises the channel index: ch = 1 for red, ch = 2 green, and ch = 3 blue channel
represent the pixel channel values of denoised and original images, respectively, and ch symbolises the channel index: ch = 1 for red, ch = 2 green, and ch = 3 blue channel
normalized colour difference (NCD) which measures the colour preservation capability of a filter:
where
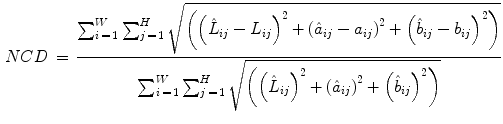
(12)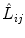 and
and 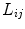 represent lightness values, and
represent lightness values, and 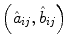 and
and 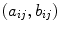 chrominance values of denoised and original images, respectively, expressed in CIELAB colour space [32]
chrominance values of denoised and original images, respectively, expressed in CIELAB colour space [32]
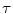 (0.0015 and 0.005) in terms of both objective error metrics criteria and visual quality [2]. Tested on Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous and Kodak Photo CD PCD0992 image data sets, it has also been verified that HSDLF performances in multichannel impulse denoising deteriorate quickly for
(0.0015 and 0.005) in terms of both objective error metrics criteria and visual quality [2]. Tested on Signal and Image Processing Institute (SIPI) Volume 3: Miscellaneous and Kodak Photo CD PCD0992 image data sets, it has also been verified that HSDLF performances in multichannel impulse denoising deteriorate quickly for 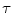
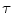
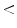 0.0012.
0.0012.Comparison of HSDLF performances in terms of used error metrics criteria for both observed values of the threshold control parameter 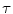 , calculated for all benchmark images is presented in Table 5. A detailed review of HSDLF performances for both observed types of impulse noise is given in Table 6.
, calculated for all benchmark images is presented in Table 5. A detailed review of HSDLF performances for both observed types of impulse noise is given in Table 6.
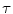 , calculated for all benchmark images is presented in Table 5. A detailed review of HSDLF performances for both observed types of impulse noise is given in Table 6.
, calculated for all benchmark images is presented in Table 5. A detailed review of HSDLF performances for both observed types of impulse noise is given in Table 6.Figures 3, 4 and 5 display the average PSNR, MAE and NCD gain values for all observed impulse denoising filters calculated over all benchmark images. Figures 6a–c, 7a–d, 8a–c, and 9a–d illustrate the visual quality of denoising results of all observed filters applied to image “Caps” corrupted by salt-and-pepper and random-valued multichannel noise, respectively.
By closely observing the results given in Tables 1, 2, 3, 4, 5 and 6 and Figs. 3, 4, 5, 6a–c, 7a–d, 8a–c, and 9a–d, following conclusions can be drawn [2]:
For all salt-and-pepper and random-valued impulse noise densities and calculated over all observed benchmark images, HSDLF performs better in more than 60% of cases for threshold control parameter value of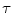 = 0.0015 than for
= 0.0015 than for 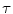 = 0.005 in terms of PSNR and MAE error metrics criteria, while NCD values are very similar for both values of
= 0.005 in terms of PSNR and MAE error metrics criteria, while NCD values are very similar for both values of 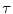 .
.
HSDLF denoising results are marginally more sensitive to shifts in values of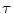 in terms of all error metrics criteria when the filter is applied to images corrupted by random-valued impulse noise.
in terms of all error metrics criteria when the filter is applied to images corrupted by random-valued impulse noise.
PSNR, MAE and NCD gains steadily rise with the increase salt-and-pepper and random-valued noise powers for both HSDLF’s values of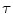 on all observed images.
on all observed images.
Table 1
Performance results of observed multichannel impulse denoising filters applied to image “Caps” (with 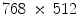 pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by
pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by  font
font
 pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by
pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by  font
fontImage:  | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
0.1 | 0.3 | 0.5 | ||||||||
Salt-and-pepper | PSNR | MAE | NCD | PSNR | MAE | NCD | PSNR | MAE | NCD | |
noise density | [dB] | [dB] | [dB] | |||||||
Denoising method | None | 17.66 | 21.36 | 0.392 | 12.89 | 42.83 | 0.708 | 10.74 | 57.86 | 0.907 |
ABVDF | 18.09 | 18.23 | 0.321 | 12.39 | 44.38 | 0.691 | 9.95 | 63.48 | 0.917 | |
ACWDDF | 20.93 | 14.13 | 0.3 | 15.11 | 32.17 | 0.621 | 12.28 | 47.09 | 0.840 | |
ACWVDF | 18.33 | 18.05 | 0.332 | 12.7 | 42.67 | 0.692 | 10.25 | 60.81 | 0.917 | |
ACWVMF | 21.88 | 13.15 | 0.301 | 16.02 | 29.39 | 0.61 | 13.12 | 42.96 | 0.824 | |
AMNFE | 25.9 | 8.65 | 0.197 | 19.41 | 20.12 | 0.427 | 15.97 | 31.13 | 0.603 | |
ASBVDF | 18.31 | 17.66 | 0.312 | 12.91 | 41.93 | 0.686 | 10.56 | 58.69 | 0.905 | |
ASDDF | 20.72 | 14.14 | 0.29 | 14.26 | 35.69 | 0.64 | 11.52 | 51.99 | 0.865 | |
ASVMF | 22.5 | 12.37 | 0.282 | 16.16 | 29.18 | 0.594 | 13.01 | 43.71 | 0.816 | |
AVMF | 20.83 | 15.01 | 0.319 | 16.02 | 29.93 | 0.609 | 13.34 | 42.15 | 0.813 | |
BVDF | 18.2 | 17.62 | 0.279 | 12.39 | 44.48 | 0.668 | 9.97 | 63.49 | 0.902 | |
DDF | 24.43 | 9.6 | 0.213 | 17.27 | 24.96 | 0.525 | 13.75 | 39.58 | 0.753 | |
EBVDF | 17.95 | 18.56 | 0.332 | 12.68 | 42.98 | 0.701 | 10.37 | 59.96 | 0.921 | |
EDDF | 20.39 | 14.38 | 0.3 | 14.08 | 35.96 | 0.65 | 11.38 | 52.47 | 0.876 | |
EVMF | 22.36 | 12.56 | 0.29 | 16.25 | 28.83 | 0.599 | 13.25 | 42.54 | 0.819 | |
FPGF | 23.31 | 11.36 | 0.263 | 17.73 | 24.18 | 0.528 | 14.39 | 37.04 | 0.745 | |
FVMF | 25.55 | 8.74 | 0.2 | 18.77 | 21.27 | 0.471 | 15.14 | 33.81 | 0.681 | |
FVMRHF | 22.95 | 11.58 | 0.276 | 16.49 | 27.68 | 0.595 | 13.4 | 41.57 | 0.816 | |
KVMF | 24.59 | 9.56 | 0.223 | 17.91 | 23.55 | 0.517 | 14.42 | 36.84 | 0.742 | |
MMF | 25.26 | 8.98 | 0.202 | 19.13 | 20.77 | 0.435 | 15.7 | 31.83 | 0.625 | |
PGF | 22.88 | 11.77 | 0.275 | 17.24 | 25.38 | 0.548 | 14.1 | 38.21 | 0.76 | |
RSBVDF | 18.38 | 18.21 | 0.344 | 13.06 | 41.24 | 0.698 | 10.71 | 57.56 | 0.913 | |
RSDDF | 21.25 | 13.56 | 0.3 | 14.55 | 34.5 | 0.648 | 11.66 | 51.05 | 0.874 | |
RSVMF | 21.94 | 12.87 | 0.297 | 15.25 | 32.09 | 0.636 | 12.23 | 47.93 | 0.862 | |
VMF | 24.73 | 9.34 | 0.211 | 17.94 | 23.49 | 0.516 | 14.44 | 36.78 | 0.742 | |
VMRHF | 22.69 | 11.93 | 0.284 | 16.37 | 28.13 | 0.602 | 13.32 | 42 | 0.823 | |
VSDROMF | 24.21 | 10.14 | 0.235 | 17.88 | 23.7 | 0.52 | 14.43 | 36.83 | 0.742 | |
HSDLF 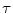 =0.005 =0.005 | 27.29 | 7.58 | 0.157 | 22.03 | 14.55 | 0.297 | 18.42 | 23.12 | 0.438 | |
HSDLF 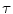 =0.0015 =0.0015 | 27.29 | 7.58 | 0.157 | 22.06 | 14.49 | 0.296 | 18.46 | 22.99 | 0.437 | |
Image:  | ||||||||||
0.1 | 0.3 | 0.5 | ||||||||
Random-valued | PSNR | MAE | NCD | PSNR | MAE | NCD | PSNR | MAE | NCD | |
noise density | [dB] | [dB] | [dB] | |||||||
Denoising method | None | 21.19 | 13.39 | 0.252 | 16.19 | 27.83 | 0.477 | 13.71 | 39.24 | 0.637 |
ABVDF | 21.6 | 11.72 | 0.211 | 15.83 | 28.53 | 0.463 | 13.12 | 42.11 | 0.636 | |
ACWDDF | 23.56 | 9.99 | 0.203 | 17.82 | 22.93 | 0.431 | 14.83 | 34.27 | 0.597 | |
ACWVDF | 21.71 | 11.71 | 0.217 | 16.04 | 27.84 | 0.464 | 13.31 | 41.03 | 0.636 | |
ACWVMF | 24.7 | 9.07 | 0.201 | 18.95 | 20.38 | 0.419 | 15.84 | 30.58 | 0.579 | |
AMNFE | 28.62 | 6.07 | 0.128 | 22.02 | 14.38 | 0.291 | 18.06 | 23.94 | 0.432 | |
ASBVDF | 22.04 | 10.76 | 0.19 | 16.23 | 27.19 | 0.451 | 13.56 | 39.81 | 0.624 | |
ASDDF | 24.53 | 8.81 | 0.182 | 17.72 | 22.98 | 0.421 | 14.52 | 35.39 | 0.595 | |
ASVMF | 25.77 | 8.12 | 0.183 | 19.51 | 19.15 | 0.398 | 16.09 | 29.69 | 0.562 | |
AVMF | 23.22 | 10.69 | 0.217 | 18.34 | 22.29 | 0.435 | 15.6 | 31.81 | 0.589 | |
BVDF | 22.03 | 10.98 | 0.17 | 15.66 | 29.34 | 0.432 | 12.84 | 44.21 | 0.615 | |
DDF | 27.42 | 6.6 | 0.136 | 20.46 | 16.88 | 0.347 | 16.67 | 27.7 | 0.513 | |
EBVDF | 21.49 | 11.63 | 0.207 | 15.93 | 28.18 | 0.465 | 13.32 | 41.04 | 0.637 | |
EDDF | 24.28 | 8.9 | 0.187 | 17.57 | 23.15 | 0.429 | 14.41 | 35.77 | 0.605 | |
EVMF | 25.54 | 8.31 | 0.189 | 19.5 | 19.14 | 0.402 | 16.16 | 29.47 | 0.565 | |
FPGF | 25.46 | 8.5 | 0.19 | 20.34 | 17.53 | 0.373 | 16.98 | 26.84 | 0.522 | |
FVMF | 28.45 | 6.01 | 0.128 | 21.74 | 14.57 | 0.311 | 17.73 | 24.45 | 0.466 | |
FVMRHF | 26.29 | 7.5 | 0.175 | 19.82 | 18.16 | 0.394 | 16.36 | 28.63 | 0.56 | |
KVMF | 27.35 | 6.84 | 0.153 | 20.88 | 16.18 | 0.348 | 17.14 | 26.24 | 0.51 | |
MMF | 28 | 6.32 | 0.134 | 21.71 | 14.95 | 0.299 | 17.9 | 24.32 | 0.439 | |
PGF | 25.33 | 8.5 | 0.191 | 19.82 | 18.41 | 0.387 | 16.59 | 27.93 | 0.539 | |
RSBVDF | 21.83 | 11.59 | 0.221 | 16.32 | 26.97 | 0.468 | 13.66 | 39.24 | 0.637 | |
RSDDF | 24.86 | 8.63 | 0.191 | 18.09 | 22.09 | 0.429 | 14.77 | 34.37 | 0.603 | |
RSVMF | 25.39 | 8.29 | 0.191 | 18.88 | 20.32 | 0.42 | 15.5 | 31.61 | 0.59 | |
VMF | 27.63 | 6.44 | 0.135 | 20.91 | 16.12 | 0.345 | 17.15 | 26.26 | 0.51 | |
VMRHF | 25.92 | 7.86 | 0.183 | 19.65 | 18.59 | 0.402 | 16.25 | 29.02 | 0.568 | |
VSDROMF | 26.49 | 7.64 | 0.17 | 20.73 | 16.70 | 0.357 | 17.11 | 26.44 | 0.514 | |
HSDLF 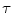 =0.005 =0.005 | 29.04 | 5.86 | 0.112 | 23.44 | 12.29 | 0.226 | 19.33 | 20.85 | 0.342 | |
HSDLF 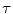 =0.0015 =0.0015 | 29.05 | 5.86 | 0.112 | 23.46 | 12.25 | 0.225 | 19.35 | 20.78 | 0.342 | |
Table 2
Performance results of observed multichannel impulse denoising filters applied to image “Parrots” (with 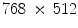 pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by
pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by  font
font
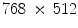 pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by
pixel image size) corrupted by various densities of salt-and-pepper and random-valued impulse noise. The best filtering performances are indicated by  font
fontImage:  | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
0.1 | 0.3 | 0.5 | ||||||||
Salt-and-pepper | PSNR | MAE | NCD | PSNR | MAE | NCD | PSNR | MAE | NCD | |
noise density | [dB] | [dB] | [dB] | |||||||
Denoising method | None | 17.51 | 21.61 | 0.341 | 12.72 | 43.45 | 0.624 | 10.53 | 58.84 | 0.809 |
ABVDF | 18.28 | 17.66 | 0.273 | 12.59 | 43.13 | 0.594 | 10.03 | 62.44 | 0.799 | |
ACWDDF | 20.89 | 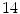 | 0.257 | 15.03 | 32.3 | 0.544 | 12.13 | 47.77 | 0.746 | |
ACWVDF | 18.43 | 17.69 | 0.283 | 12.86 | 41.7 | 0.598 | 10.29 | 60.15 | 0.803 | |
ACWVMF | 21.73 | 13.21 | 0.26 | 15.82 | 29.93 | 0.536 | 12.83 | 44.23 | 0.735 | |
AMNFE | 25.87 | 8.5 | 0.169 | 19.07 | 20.81 | 0.382 | 15.46 | 33.05 | 0.553 | |
ASBVDF | 18.55 | 17.01 | 0.263 | 12.99 | 41.31 | 0.594 | 10.53 | 58.51 | 0.795 | |
ASDDF | 20.68 | 14.05 | 0.25 | 14.28 | 35.44 | 0.557 | 11.41 | 52.37 | 0.764 | |
ASVMF | 22.36 | 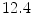 | 0.243 | 15.98 | 29.67 | 0.522 | 12.75 | 44.84 | 0.728 | |
AVMF | 20.77 | 15.01 | 0.274 | 15.87 | 30.33 | 0.534 | 13.07 | 43.31 | 0.725 | |
BVDF | 18.77 | 16.07 | 0.23 | 12.78 | 42 | 0.565 | 10.14 | 61.63 | 0.78 | |
DDF | 24.49 | 9.29 | 0.181 | 17.14 | 25.31 | 0.464 | 13.52 | 40.62 | 0.674 | |
EBVDF | 18.2 | 17.92 | 0.283 | 12.8 | 42.18 | 0.607 | 10.38 | 59.59 | 0.809 | |
EDDF | 20.51 | 14.17 | 0.258 | 14.15 | 35.61 | 0.566 | 11.3 | 52.71 | 0.774 | |
EVMF | 22.23 | 12.59 | 0.251 | 16.04 | 29.39 | 0.528 | 12.95 | 43.82 | 0.731 | |
FPGF | 23.16 | 11.33 | 0.227 | 17.48 | 24.77 | 0.468 | 14.01 | 38.58 | 0.671 | |
FVMF | 25.54 | 8.53 | 0.171 | 18.48 | 21.87 | 0.418 | 14.72 | 35.41 | 0.617 | |
FVMRHF | 22.77 | 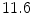 | 0.239 | 16.25 | 28.34 | 0.525 | 13.07 | 42.99 | 0.73 | |
KVMF | 24.53 | 9.4 | 0.191 | 17.64 | 24.14 | 0.459 | 14.05 | 38.37 | 0.668 | |
MMF | 25.21 | 8.81 | 0.174 | 18.8 | 21.47 | 0.389 | 15.22 | 33.69 | 0.572 | |
PGF | 22.92 | 11.58 | 0.233 | 17.06 | 25.8 | 0.482 | 13.77 | 39.57 | 0.682 | |
RSBVDF | 18.47 | 17.91 | 0.295 | 13.05 | 41.11 | 0.609 | 10.62 | 57.8 | 0.806 | |
RSDDF | 21.18 | 13.51 | 0.258 | 14.51 | 34.52 | 0.566 | 11.53 | 51.56 | 0.774 | |
RSVMF | 21.79 | 12.92 | 0.256 | 15.07 | 32.6 | 0.559 | 12 | 48.94 | 0.768 | |
VMF | 24.72 | 9.12 | 0.181 | 17.67 | 24.08 | 0.458 | 14.07 | 38.31 | 0.668 | |
VMRHF | 22.53 | 11.94 | 0.245 | 16.12 | 28.77 | 0.531 | 13 | 43.4 | 0.735 | |
VSDROMF | 24.21 | 9.94 | 0.2 | 17.62 | 24.29 | 0.461 | 14.06 | 38.37 | 0.668 | |
HSDLF 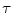 =0.005 =0.005 | 27 | 7.64 | 0.14 | 21.34 | 15.95 | 0.283 | 17.54 | 26.13 | 0.428 | |
HSDLF 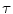 =0.0015 =0.0015 | 27 | 7.64 | 0.14 | 21.36 | 15.89 | 0.283 | 17.57 | 26 | 0.428 | |
Image: 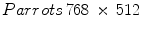 | ||||||||||
0.1 | 0.3 | 0.5 | ||||||||
Random-valued | PSNR | MAE | NCD | PSNR | MAE | NCD | PSNR | MAE | NCD | |
noise density | [dB] | [dB] | [dB] | |||||||
Denoising method | None | 20.85 | 13.99 | 0.226 | 15.78 | 29.34 | 0.436 | 13.28 | 41.48 | 0.59 |
ABVDF | 21.48 | 11.93 | 0.187 | 15.76 | 29 | 0.416 | 12.99 | 43.2 | 0.58 | |
ACWDDF | 23.33 | 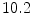 | 0.18 | 17.47 | 23.92 | 0.392 | 14.45 | 36.15 | 0.551 | |
ACWVDF | 21.62 | 11.88 | 0.191 | 15.94 | 28.39 | 0.418 | 13.15 | 42.27 | 0.582 | |
ACWVMF | 24.34 | 9.4 | 0.179 | 18.41 | 21.69 | 0.384 | 15.27 | 32.95 | 0.539 | |
AMNFE | 28.46 | 6.07 | 0.115 | 21.29 | 15.78 | 0.275 | 17.27 | 27 | 0.418 | |
ASBVDF | 22.12 | 10.72 | 0.166 | 16.11 | 27.76 | 0.405 | 13.33 | 41.27 | 0.571 | |
ASDDF | 24.24 | 9.05 | 0.162 | 17.46 | 23.84 |
|||||