Fig. 1
Examples of datasets in our studies: a Sagittal view of restricted FOV near the chest area only; b Coronal view of disease-affected spine; c Sagittal view of full-body scan. Two additional transverse planes show that the spinal canal is not always contoured by bones
Interactive segmentation has also developed rapidly and drawn many successes in past decades. By allowing users to define initial seeds, the interactive mechanism is able to understand image content better and generate improved segmentation results in the end. We refer readers to [8] for a comprehensive survey of interactive segmentation methods. Among them, random walks (RW) [9] has been widely applied in various studies. RW asks users to specify seeding voxels of different labels, and then assigns labels to non-seeding voxels by embedding the image into a graph and utilizing intensity similarity between voxels. Users can edit the placement of seeds in order to acquire more satisfactory results.
In this paper, we adapt the idea of interactive segmentation to form a fully auto-matic approach that segments spinal canals from CT images. Different from manually editing seeds in the interactive mode, our method refines the topology of the spinal canal and improves segmentation in the automatic and iterative manner. To start the automatic pipeline, we identify voxels that are inside the spinal canal according to their appearance features [10]. For convenience, we will denote the voxels inside the spinal canal as foreground, and background otherwise. Then the detected seeds are input to RW and produce the segmentation of foreground/background. Based on the tentative segmentation, we extract and further refine the topology of the spinal canal by considering both geometry and appearance constraints. Seeds are adjusted accordingly and fed back to RW for better segmentation. By iteratively applying this scheme, we are able to cascade several RW solvers and build a highly reliable method to segment spinal canals from CT images, even under challenging conditions.
Our method and its bottom-up design, significantly different from the top-down parcellation in other solutions, utilize both population-based appearance information and subject-specific geometry model. With limited training subjects, we are able to locate enough seeding voxels to initialize segmentation and iteratively improve the results by learning spinal canal topologies that vary significantly across patients. We will detail our method in Sect. 2, and show experimental results in Sect. 3.
2 Method
We treat segmenting spinal canal as a binary segmentation problem. Let 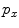 denote the probability of the voxel
denote the probability of the voxel 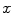 being foreground (inside spinal canal) after voxel classification and
being foreground (inside spinal canal) after voxel classification and 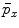 for background, respectively. In general, we have
for background, respectively. In general, we have 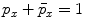 after normalization. The binary segmentation can be acquired by applying a threshold to
after normalization. The binary segmentation can be acquired by applying a threshold to 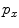 . Although shapes of spinal canals can vary significantly across the population, they are tubular structures in general. We start from a small set of foreground voxels with very high classification confidences. These voxels act as positive seeds in RW to generate conservative segmentation with relatively low sensitivity but also low false positives (FP). All foreground voxels are assumed to form a continuous and smooth anatomic topology, which refines the seed points in order to better approximate the structure of the spinal canal. Hence the sensitivity of the RW segmentation increases with the new seeds. By iteratively feeding the improved seeds to RW, we have successfully formed an automatic pipeline that yields satisfactory segmentation of spinal canals.
. Although shapes of spinal canals can vary significantly across the population, they are tubular structures in general. We start from a small set of foreground voxels with very high classification confidences. These voxels act as positive seeds in RW to generate conservative segmentation with relatively low sensitivity but also low false positives (FP). All foreground voxels are assumed to form a continuous and smooth anatomic topology, which refines the seed points in order to better approximate the structure of the spinal canal. Hence the sensitivity of the RW segmentation increases with the new seeds. By iteratively feeding the improved seeds to RW, we have successfully formed an automatic pipeline that yields satisfactory segmentation of spinal canals.
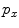 denote the probability of the voxel
denote the probability of the voxel 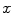 being foreground (inside spinal canal) after voxel classification and
being foreground (inside spinal canal) after voxel classification and 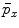 for background, respectively. In general, we have
for background, respectively. In general, we have 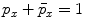 after normalization. The binary segmentation can be acquired by applying a threshold to
after normalization. The binary segmentation can be acquired by applying a threshold to 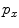 . Although shapes of spinal canals can vary significantly across the population, they are tubular structures in general. We start from a small set of foreground voxels with very high classification confidences. These voxels act as positive seeds in RW to generate conservative segmentation with relatively low sensitivity but also low false positives (FP). All foreground voxels are assumed to form a continuous and smooth anatomic topology, which refines the seed points in order to better approximate the structure of the spinal canal. Hence the sensitivity of the RW segmentation increases with the new seeds. By iteratively feeding the improved seeds to RW, we have successfully formed an automatic pipeline that yields satisfactory segmentation of spinal canals.
. Although shapes of spinal canals can vary significantly across the population, they are tubular structures in general. We start from a small set of foreground voxels with very high classification confidences. These voxels act as positive seeds in RW to generate conservative segmentation with relatively low sensitivity but also low false positives (FP). All foreground voxels are assumed to form a continuous and smooth anatomic topology, which refines the seed points in order to better approximate the structure of the spinal canal. Hence the sensitivity of the RW segmentation increases with the new seeds. By iteratively feeding the improved seeds to RW, we have successfully formed an automatic pipeline that yields satisfactory segmentation of spinal canals.2.1 Voxelwise Classification
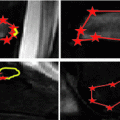
In order to identify highly reliable foreground voxels as positive seeds, we turn to voxelwise classification via supervised learning. We have manually annotated the medial lines of spinal canals on 20 CT datasets. Voxels exactly along the medial lines are sampled as foreground, while background candidates are obtained from a constant distance away to the medial lines. We further use 3D Haar features as voxel descriptors. With varying sizes of detection windows, an abundant collection of Haar features is efficiently computed for each voxel. The probabilistic boosting tree (PBT) classifiers are then trained with AdaBoost nodes [11]. We have cascaded multiple PBT classifiers that work in coarse-to-fine resolutions. In this way, we not only speed up the detection in early stage by reducing the number of samples, but also exploit features benefiting from higher scales of Haar wavelets in coarse resolution. Note that similar strategy is also successfully applied in other studies [10]. The well-performing foreground voxel confidence map (as well as the measuring color map) with respect to a training subject is displayed in Fig. 2a. However, when applied to a new testing dataset (e.g., Fig. 2c–d), the classifiers may suffer from both false negative (FN) and FP errors. For instance, an FP artifact is highlighted in Fig. 2b. Figure 2c shows discontinuity of foreground confidence due to FN errors. Since the purpose here is to preserve highly reliable foreground voxels only (i.e., Fig. 2d), we have adopted a high confidence threshold (![$$>$$” src=”/wp-content/uploads/2016/03/A323246_1_En_2_Chapter_IEq6.gif”></SPAN>0.9) empirically to suppress most FP errors. The detection sensitivity will be subsequently improved as follows.<br />
<DIV id=Fig2 class=Figure><br />
<DIV id=MO2 class=MediaObject><IMG alt=A323246_1_En_2_Fig2_HTML.jpg src=]()
Fig. 2
Panel a shows the confidence map output by voxelwise classification on a training subject; panels b–d are for the voxelwise confidences of another testing dataset. Among them, FP errors and FN errors are highlighted in b and c, respectively. We use a high confidence threshold to preserve reliable foreground voxels only as in d
2.2 Random Walks
Similar to PBT-based classification, RW also produces voxelwise likelihoods of being foreground/background [9]. After users have specified foreground/background seeds, RW departs from a certain non-seeding voxel and calculates its probabilities to reach foreground and background seeds, as 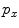 and
and 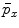 , respectively. Usually the non-seeding voxel
, respectively. Usually the non-seeding voxel 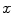 is assigned to foreground if
is assigned to foreground if ![$$p_x>\bar{p}_x$$” src=”/wp-content/uploads/2016/03/A323246_1_En_2_Chapter_IEq10.gif”></SPAN>. In the context of RW, the image is embedded into a graph where vertices correspond to individual voxels and edges link neighboring voxels. The weight <SPAN id=IEq11 class=InlineEquation><IMG alt=$$\textit{w}_{xy}$$ src=]() of the edge
of the edge 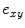 , which measures the similarity between two neighboring voxels
, which measures the similarity between two neighboring voxels 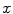 and
and 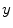 , is defined as
, is defined as
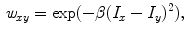
where 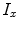 and
and 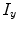 represent intensities at two locations;
represent intensities at two locations; 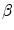 a positive constant. Assuming segmentation boundaries to be coincident with intensity changes, RW aims to estimate
a positive constant. Assuming segmentation boundaries to be coincident with intensity changes, RW aims to estimate 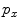




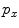 and
and 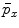 , respectively. Usually the non-seeding voxel
, respectively. Usually the non-seeding voxel 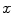 is assigned to foreground if
is assigned to foreground if 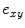 , which measures the similarity between two neighboring voxels
, which measures the similarity between two neighboring voxels 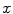 and
and 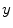 , is defined as
, is defined as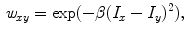
(1)
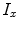 and
and 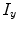 represent intensities at two locations;
represent intensities at two locations; 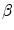 a positive constant. Assuming segmentation boundaries to be coincident with intensity changes, RW aims to estimate
a positive constant. Assuming segmentation boundaries to be coincident with intensity changes, RW aims to estimate 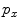
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree