Fig. 1
The region of interest in our experiment: a A clinical CT slice of a human vertebra. b The blue color shows the VB region
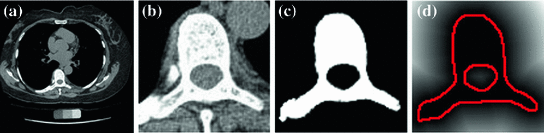
Fig. 2
An example of the initial labeling. a Original CT image, b detection of the VB region using MF, c the initial labeling, f* using tensor level set segmentation and d the SDF of the initial segmentation (f*) which is used in the registration phase. Red color shows the zero level contour
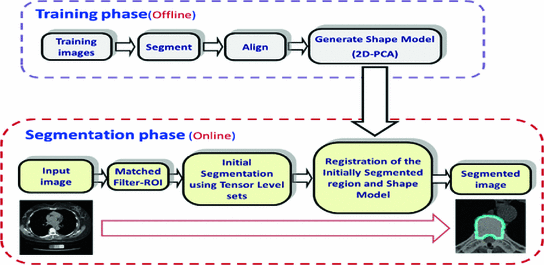
Fig. 3
Our proposed shape-based segmentation. Our framework consists of two main stages; the training phase and the segmentation phase
2 Methods
Intensity based model may not be enough to obtain the optimum segmentation. Hence, we propose a new shape based segmentation method. This method has several steps. As a pre-processing step, we extract the human spine area using the Matched filter (MF) adopted in [6]. As shown in Fig. 2a, b, the MF is employed to detect the VB automatically. This process helps to roughly remove the spinous processes and pedicles. Additionally, it eliminates the user interaction. We tested the Matched filter using 3,000 clinical CT images. The VB detection accuracy is 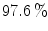 . In the second phase, we obtain initial labeling (f*) using the region-based tensor level set model, as described in [14]. Finally, we register the initial labeled image and the shape priors to obtain the optimum labeling, as in [1]. To obtain the shape priors (p), we use the 2D-PCA on all training images. Figure 3 summarizes the main components of our framework. The following sections give more details about the shape model construction and the segmentation method.
. In the second phase, we obtain initial labeling (f*) using the region-based tensor level set model, as described in [14]. Finally, we register the initial labeled image and the shape priors to obtain the optimum labeling, as in [1]. To obtain the shape priors (p), we use the 2D-PCA on all training images. Figure 3 summarizes the main components of our framework. The following sections give more details about the shape model construction and the segmentation method.
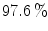 . In the second phase, we obtain initial labeling (f*) using the region-based tensor level set model, as described in [14]. Finally, we register the initial labeled image and the shape priors to obtain the optimum labeling, as in [1]. To obtain the shape priors (p), we use the 2D-PCA on all training images. Figure 3 summarizes the main components of our framework. The following sections give more details about the shape model construction and the segmentation method.
. In the second phase, we obtain initial labeling (f*) using the region-based tensor level set model, as described in [14]. Finally, we register the initial labeled image and the shape priors to obtain the optimum labeling, as in [1]. To obtain the shape priors (p), we use the 2D-PCA on all training images. Figure 3 summarizes the main components of our framework. The following sections give more details about the shape model construction and the segmentation method.2.1 Shape Model Construction
In this work, we describe the shape representation using the SDF, as in [2]. The objective of this step is to obtain the most important information of training images using 2D-PCA. As op-posed to conventional PCA, 2D-PCA is based on 2D matrix rather than 1D vector. This means that, the image does not need to be pre-transformed into a vector. In addition, the image covariance matrix(G) can be directly constructed using the original image matrices. As a result, 2D-PCA has two important advantages over PCA. First, it is easier to evaluate G accurately since its size using 2D-PCA is much smaller. Second, less time is required to determine the corresponding eigenvectors [15]. 2D-PCA projects an image matrix X, which is an mn matrix onto a vector, b, which is an n1 vector, by the linear transformation. The resultant projection coefficient vector y will be:
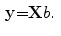
Suppose that there are M training images, the ith training image is denoted by 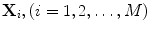 and the average image of all training samples is denoted by
and the average image of all training samples is denoted by 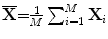 . Then, let us define the image covariance matrix G, as in [15]:
. Then, let us define the image covariance matrix G, as in [15]:
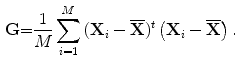
It is clear that, the matrix G is 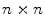 nonnegative definite matrix. Similar to PCA, the goal of 2D-PCA is to find a projection axis that maximizes
nonnegative definite matrix. Similar to PCA, the goal of 2D-PCA is to find a projection axis that maximizes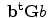 . The optimal K projection axes b
. The optimal K projection axes b 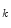 , where k =1, 2, …, K, that maximize the above criterion are the eigenvectors of G corresponding to the largest K eigenvalues. For an image X, we can use its reconstruction
, where k =1, 2, …, K, that maximize the above criterion are the eigenvectors of G corresponding to the largest K eigenvalues. For an image X, we can use its reconstruction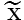 defined below to approximate it.
defined below to approximate it.
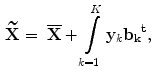
where 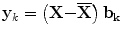 is called the
is called the 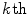 principal component vector of the sample image X. The principal component vectors obtained are used to form an
principal component vector of the sample image X. The principal component vectors obtained are used to form an 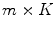 matrix Y = [y
matrix Y = [y 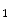 ,y
,y 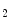 ,…,y
,…,y 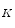 ] and let B = [b
] and let B = [b 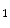 ,b
,b 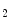 ,…,b
,…,b 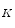 ], then we can rewrite Eq. 3 as:
], then we can rewrite Eq. 3 as:
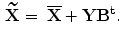
However, one disadvantage of 2D-PCA (compared to PCA) is that more coefficients are needed to represent an image. From Eq. 4, it is clear that dimension of the 2D-PCA principal component matrix Y (m  K) is always much higher than PCA. To reduce the dimension of matrix Y, the conventional PCA is used for further dimensional reduction after 2D-PCA. More details will be discussed in the following section.
K) is always much higher than PCA. To reduce the dimension of matrix Y, the conventional PCA is used for further dimensional reduction after 2D-PCA. More details will be discussed in the following section.
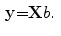
(1)
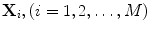 and the average image of all training samples is denoted by
and the average image of all training samples is denoted by 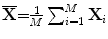 . Then, let us define the image covariance matrix G, as in [15]:
. Then, let us define the image covariance matrix G, as in [15]: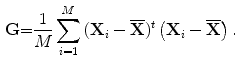
(2)
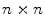 nonnegative definite matrix. Similar to PCA, the goal of 2D-PCA is to find a projection axis that maximizes
nonnegative definite matrix. Similar to PCA, the goal of 2D-PCA is to find a projection axis that maximizes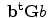 . The optimal K projection axes b
. The optimal K projection axes b 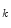 , where k =1, 2, …, K, that maximize the above criterion are the eigenvectors of G corresponding to the largest K eigenvalues. For an image X, we can use its reconstruction
, where k =1, 2, …, K, that maximize the above criterion are the eigenvectors of G corresponding to the largest K eigenvalues. For an image X, we can use its reconstruction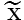 defined below to approximate it.
defined below to approximate it.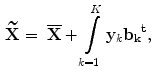
(3)
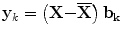 is called the
is called the 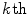 principal component vector of the sample image X. The principal component vectors obtained are used to form an
principal component vector of the sample image X. The principal component vectors obtained are used to form an 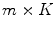 matrix Y = [y
matrix Y = [y 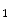 ,y
,y 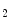 ,…,y
,…,y 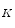 ] and let B = [b
] and let B = [b 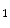 ,b
,b 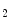 ,…,b
,…,b 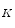 ], then we can rewrite Eq. 3 as:
], then we can rewrite Eq. 3 as: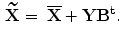
(4)
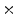 K) is always much higher than PCA. To reduce the dimension of matrix Y, the conventional PCA is used for further dimensional reduction after 2D-PCA. More details will be discussed in the following section.
K) is always much higher than PCA. To reduce the dimension of matrix Y, the conventional PCA is used for further dimensional reduction after 2D-PCA. More details will be discussed in the following section.Now, let the training set consists of M training images {I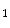 ,…, I
,…, I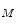 }; with SDFs
}; with SDFs 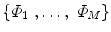 . All images are binary, pre-aligned, and normalized to the same resolution. As in [2], we obtain the mean level set function of the training shapes,
. All images are binary, pre-aligned, and normalized to the same resolution. As in [2], we obtain the mean level set function of the training shapes, 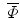 , as the average of these M signed distance functions. To extract the shape variabilities,
, as the average of these M signed distance functions. To extract the shape variabilities, 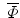 is subtracted from each of the training SDFs. The obtained mean-offset functions can be represented as {
is subtracted from each of the training SDFs. The obtained mean-offset functions can be represented as {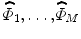 }. These new functions are used to measure the variabilities of the training images. We use 80 training VB images with
}. These new functions are used to measure the variabilities of the training images. We use 80 training VB images with 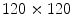 pixels in our experiment. According (2), the constructed matrix G will be:
pixels in our experiment. According (2), the constructed matrix G will be:
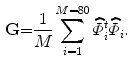
Experimentally, we find that, the minimum suitable value is 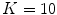 . Less than this value, the accuracy of our segmentation algorithm falls drastically. After choosing the eigenvectors corresponding to 10 largest eigenvalues, b
. Less than this value, the accuracy of our segmentation algorithm falls drastically. After choosing the eigenvectors corresponding to 10 largest eigenvalues, b 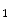 , b
, b 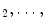 b
b 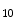 , we obtained the principal component matrix Y
, we obtained the principal component matrix Y 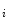 (
(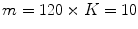 ) for each SDF of our training set (
) for each SDF of our training set (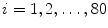 ). For more dimensional reduction, the conventional PCA is applied on the principal components {
). For more dimensional reduction, the conventional PCA is applied on the principal components {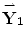 ,…,
,…, 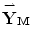 }. It should be noted that,
}. It should be noted that, 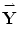 is the vector representation of Y. The reconstructed components (after retransforming to matrix representation) will be:
is the vector representation of Y. The reconstructed components (after retransforming to matrix representation) will be:
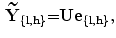
where U is the matrix which contains L eigenvectors corresponding to L largest eigenvalues 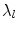 , (
, (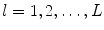 ), and
), and 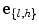 is the set of model parameters which can be described as
is the set of model parameters which can be described as
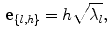
where 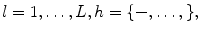 and is a constant which can be chosen arbitrarily (in our experiments, we chose
and is a constant which can be chosen arbitrarily (in our experiments, we chose 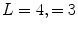 ). The new principal components of training SDFs are represented as {
). The new principal components of training SDFs are represented as {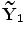 ,…,
,…,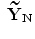 } instead of {
} instead of {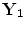 ,…,
,…,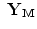 } where N is the multiplication of L and standard deviation in eigenvalues (the number of elements in h), i.e.
} where N is the multiplication of L and standard deviation in eigenvalues (the number of elements in h), i.e. 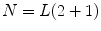 . Given the set {
. Given the set {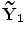 ,…,
,…,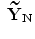 },the new projected training SDFs are obtained as follows:
},the new projected training SDFs are obtained as follows:
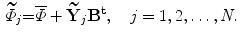
Finally, the shape model is required to capture the variations in the training set. This model is considered to be a weighted sum of the projected SDFs (Eq. 8




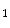 ,…, I
,…, I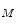 }; with SDFs
}; with SDFs 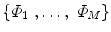 . All images are binary, pre-aligned, and normalized to the same resolution. As in [2], we obtain the mean level set function of the training shapes,
. All images are binary, pre-aligned, and normalized to the same resolution. As in [2], we obtain the mean level set function of the training shapes, 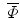 , as the average of these M signed distance functions. To extract the shape variabilities,
, as the average of these M signed distance functions. To extract the shape variabilities, 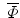 is subtracted from each of the training SDFs. The obtained mean-offset functions can be represented as {
is subtracted from each of the training SDFs. The obtained mean-offset functions can be represented as {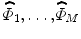 }. These new functions are used to measure the variabilities of the training images. We use 80 training VB images with
}. These new functions are used to measure the variabilities of the training images. We use 80 training VB images with 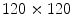 pixels in our experiment. According (2), the constructed matrix G will be:
pixels in our experiment. According (2), the constructed matrix G will be: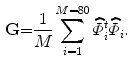
(5)
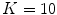 . Less than this value, the accuracy of our segmentation algorithm falls drastically. After choosing the eigenvectors corresponding to 10 largest eigenvalues, b
. Less than this value, the accuracy of our segmentation algorithm falls drastically. After choosing the eigenvectors corresponding to 10 largest eigenvalues, b 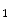 , b
, b 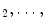 b
b 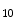 , we obtained the principal component matrix Y
, we obtained the principal component matrix Y 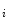 (
(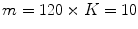 ) for each SDF of our training set (
) for each SDF of our training set (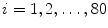 ). For more dimensional reduction, the conventional PCA is applied on the principal components {
). For more dimensional reduction, the conventional PCA is applied on the principal components {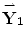 ,…,
,…, 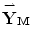 }. It should be noted that,
}. It should be noted that, 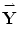 is the vector representation of Y. The reconstructed components (after retransforming to matrix representation) will be:
is the vector representation of Y. The reconstructed components (after retransforming to matrix representation) will be: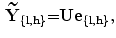
(6)
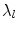 , (
, (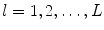 ), and
), and 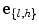 is the set of model parameters which can be described as
is the set of model parameters which can be described as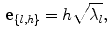
(7)
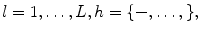 and is a constant which can be chosen arbitrarily (in our experiments, we chose
and is a constant which can be chosen arbitrarily (in our experiments, we chose 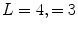 ). The new principal components of training SDFs are represented as {
). The new principal components of training SDFs are represented as {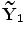 ,…,
,…,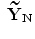 } instead of {
} instead of {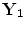 ,…,
,…,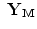 } where N is the multiplication of L and standard deviation in eigenvalues (the number of elements in h), i.e.
} where N is the multiplication of L and standard deviation in eigenvalues (the number of elements in h), i.e. 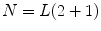 . Given the set {
. Given the set {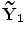 ,…,
,…,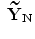 },the new projected training SDFs are obtained as follows:
},the new projected training SDFs are obtained as follows: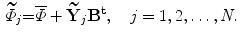
(8)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree