Fig. 1.1
The hydrogen nucleus spins around its own axis, generating an intrinsic magnetic vector M i , which in turn makes the nucleus precess with the Larmor rotation frequency v 0 about the direction of the external field B 0
Without external influences, the intrinsic magnetic vectors of nuclei in a normal tissue sample are pointing in completely random directions. Hence, from a macroscopic perspective these vectors are averaging themselves out to zero net magnetization.
When placing nuclei in an external magnetic field, B 0, the intrinsic magnetic vector of each nucleus will align along the direction of this field.1 However, this alignment will not make the vectors become strictly parallel to the B 0 field. Instead, the nuclei will start to precess around the axis of the B 0 field, making the intrinsic magnetic vectors circle at an angle around this direction. This circling will occur with a rotational frequency called the Larmor frequency, v 0 (Fig. 1.1), which varies with the strength of the external B 0 field by
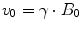
where γ is a nuclei-specific constant called the gyromagnetic ratio (γ = 42.6 MHz/T for the hydrogen nucleus).
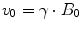
(1.1)
In any tissue sample, even an extremely small volume contains many millions of hydrogen nuclei. For this reason, it is instructive to consider a large number of nuclei as a single unit, called an isochromat (Fig. 1.2). The intrinsic magnetic vectors of each nucleus in an isochromat are all circling around the B 0 field, but at random angular positions. Thus, adding all intrinsic vectors of the isochromat together results in a bulk magnetization vector, M, pointing in the same direction as the B 0 field.
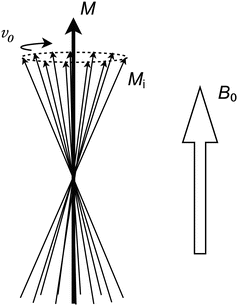

Fig. 1.2
Each individual intrinsic M i vector has a random angular position. Thus, the sum of all M i vectors in an isochromat is a new vector, M, pointing in the same direction as the externally applied B 0 field
Coils and RF Pulses
In order to interact with the precessing nuclei, radio frequency (RF) magnetic pulses are used. Such pulses are generated and received by coils, which must be placed in the vicinity of the tissue to be imaged. Coils are available in a variety of types and are usually shaped to come as close as possible to the tissue of interest. For example, for brain imaging a cylindrically shaped coil is often used, efficiently surrounding the entire head, whereas for hip imaging a flat flexible coil that can be directly strapped onto the body surface is more feasible.
In order for the coil to generate an RF pulse, a current oscillating with the Larmor frequency is passed through it. The oscillating magnetic field generated by this current can be divided into separate components. Of particular interest is the component that is perpendicular to the B 0 field, which can be thought of as an additional, weaker magnetic field (called the B 1 field) rotating around the B 0 direction (Fig. 1.3).

Fig. 1.3
The RF pulse can be thought of as a magnetic B 1 field rotating around the B 0 direction. The nuclei will then precess around both the B 0 and the B 1 fields, which results in the M vector spiraling away from the B 0 direction
From the nuclei’s perspective there are now two concurrent magnetic fields around which they will precess. Since one is a strong stationary field (B 0) and the other is a weak rotating field (B 1), the result is that the bulk magnetization vector M will spiral itself away from the B 0 direction at a relatively slow speed. This spiraling will proceed for the duration of the RF pulse. An RF pulse is characterized by the resulting angle between the magnetization vector M and the B 0 direction. This flip angle is primarily determined by the duration (typically 0.5–5 ms) and the amplitude of the pulse.
As soon as the M vector points away from the B 0 direction it will no longer be time and space invariant. Instead, it will rotate around the B 0 direction. Thus, the nuclei themselves generate an oscillating magnetic field, which will induce a signal in the conductors of the receiver coil. At this point the spinning nuclei are said to be excited and the associated RF pulse is often referred to as an excitation pulse. The signal that follows immediately after excitation is denoted free induction decay (FID). However, in clinical MRI other types of signals are more commonly used, which requires a few additional steps to generate. Such signals are referred to as echoes and are described later in this chapter.
For a 90° excitation pulse flip angle the M vector is turned perpendicular to the B 0 field and the generated signal will have its maximum amplitude.
T 1, T 2, and Proton Density
There are three primary parameters required in order to describe the spin-behavior of a set of hydrogen nuclei. These are the T 1, T 2, and proton density (PD) parameters. In most MR images the contrasts origin from the variation of these parameters between tissue types.
The proton density is the most intuitive parameter, as the number of hydrogen nuclei per unit volume is directly proportional to the amplitude of the signal generated by these nuclei. However, in clinical MRI this parameter is often not of primary interest, as it does not provide much information about the chemical composition of the tissue.
The T 1 parameter is a measure of how fast the longitudinal (parallel to B 0) magnetization recovers (Fig. 1.4). When the magnetization vector M is perturbed by an RF pulse, it will take a certain amount of time until it has recovered back to its equilibrium state (i.e., when the isochromats are fully relaxed). This recovery occurs exponentially with time and is characterized by the T 1 parameter, which can be thought of as the time it takes for the nuclei to recover 63 % of the longitudinal magnetization that was lost when the RF pulse was applied.
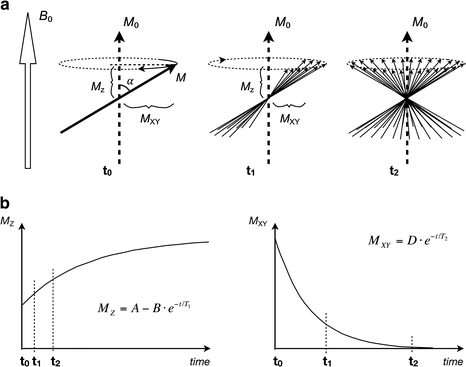

Fig. 1.4
(a) Immediately after an RF pulse (t 0) the magnetization vector M is perturbed from its initial M 0 direction by a flip angle α. M z is the remaining longitudinal magnetization, which will eventually recover to back to M 0. At this point, the transverse magnetization component M xy is time variant, allowing a signal to be induced in an external pickup coil. A short while later (t 1) the individual spinning nuclei that make up the M vector have dephased somewhat, resulting in a smaller time variant component M xy and a decreased amplitude of the induced signal. After yet another while (t 2) the spinning nuclei have dephased totally, resulting in no time variant component at all. At this point, no signal will be induced in the external coil. The dephasing time is characterized by the T 2 parameter. (b) The longitudinal magnetization (left) recovers exponentially at a rate determined by T 1. The transverse magnetization (right) decays exponentially at a rate determined by T 2. The transverse magnetization always decays much faster than the longitudinal magnetization recovers. Time points t 0, t 1, and t 2 refer to illustrated states in (a)
The T 2 parameter is a measure of how fast the transverse (perpendicular to B 0) magnetization decays (Fig. 1.4). It can be pictured by considering an isochromat immediately after an RF pulse, at which time the M vector has a large rotating transverse component, which can induce a current in an external pickup coil. After a short while, the intrinsic vectors that make up the isochromat will dephase and point in slightly different directions, resulting in a reduction of the rotating component of the M vector. After yet another while the intrinsic vectors are completely dephased, leaving no rotating component at all. This decline occurs exponentially with time and is characterized by the T 2 parameter, which can be thought of as the time it takes for the transverse magnetization to decline to 37 % of what it was immediately after the RF pulse.
Any individual nucleus is surrounded by millions of other nuclei. Since all nuclei possess some type of motion (Brownian motion, tumbling motion, etc.), the intrinsic magnetic vectors of all these nearby nuclei will summarize into a slightly fluctuating magnetic field that is superimposed onto the static B 0 field.
The component of this fluctuating magnetic field that is perpendicular to the B 0 field will reveal itself to the nuclei as an additional vector around which they will try to precess. Even though this vector is not strong enough to cause actual precession (as the B 0 and B 1 fields do), it is strong enough to affect the longitudinal relaxation behavior of the nuclei. Thus, this describes one of the primary effects determining the T 1 value.
The other component of the fluctuating magnetic field, parallel to the B 0 field, will add scalar to the B 0 field strength, causing a slight fluctuation of Larmor frequency between individual nuclei. This effect is one of the primary reasons for T 2 relaxation, since a variation in Larmor frequency for nuclei within an isochromat causes its compounding intrinsic magnetic vectors to dephase.
As can be understood, both the T 1 and T 2 relaxation times are determined by the combined characteristics of the fluctuating magnetic fields that are present within a sample. As such, there are no simple rules as to what the T 1 and T 2 values will be for a specific tissue. In general, the T 1 and T 2 values are dependent on what types of bindings exist between hydrogen nuclei and their surroundings, as well as the mobility of the nuclei. For example, in very low-viscous fluids such as cerebrospinal fluid (CSF) the hydrogen mobility results in very long T 1 values (2,000–3,000 ms), whereas it is very short in fatty tissue (down to 100 ms) where the motion of the nuclei is much more restricted.
In a perfect measurement setup the signal picked up by the receiver coil would strictly follow the decay of the transverse T 2 magnetization, as is described above. However, in practice there are always local inhomogeneities in the applied B 0 field, causing additional variation in Larmor frequency between nuclei and thereby making the nuclei dephase faster than predicted by the T 2 value. These local inhomogeneities are a result of macroscopic effects, such as the technical difficulties of designing an absolutely homogenous magnet in combination with magnetic susceptibility variation between different tissue types. Compared to the mechanism governing the T 2 decay, these local inhomogeneities are static in the sense that they will not vary with time at a specific location. Thus, the dephasing caused by such local inhomogeneities can be reversed using refocusing RF pulses, which is described later in this chapter. The combination of T 2 decay and the decay caused by local inhomogeneities is usually referred to as T 2* decay.
Magnetic Field Gradients
In order to form images it is necessary to be able to differentiate between signals coming from nuclei in different parts of the subject. This is achieved using the gradient coils.
The gradient coils generate magnetic fields that are designed such that they vary in strength along their axis of operation (Fig. 1.5). When a gradient is switched on, its field will superimpose onto the static B 0 field. The total magnetic field strength will then be somewhat higher in one end of the investigated volume and somewhat lower in the other end. Hence, the Larmor frequency of the nuclei in the volume will also vary throughout the different positions. This is the effect used to form images.
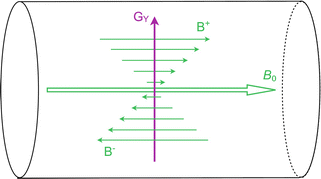

Fig. 1.5
In this figure the y-gradient (G Y ) is illustrated inside the MRI scanner, although the principle is the same also for the x and z-gradients. When the gradient is operated, its field (B+ trough B−) will add onto the static B 0 field, so that the total magnetic field is somewhat higher in the upper part of the bore and somewhat lower in the bottom part. Thus, the Larmor frequency of nuclei will vary depending on where they are located. The strength of the gradient can be arbitrarily adjusted by the MRI scanner
There are three sets of gradient coils in a clinical MRI scanner, generating magnetic field gradients in three orthogonal directions (x, y and z direction). The strength of each gradient can be arbitrarily adjusted by the MRI scanner. By combining these three gradient coils (i.e., running them simultaneously and at different strengths) apparent magnetic field gradients can be generated in any direction. There are typically three different ways to use the gradients for encoding spatial information:
1.
Applying a narrow-band RF pulse while a magnetic field gradient is switched on will exclude all nuclei whose Larmor frequencies are outside of the RF pulse bandwidth, meaning that a specific section through the tissue can be selected for excitation. This is referred to as a spatially selective gradient. A slice-selection gradient is a commonly used spatially selective gradient.
2.
Applying a gradient for a short while immediately after an RF pulse will create a difference in phase of signals emitted from nuclei at different positions. The phase can be thought of as a measure of how well the emitted signals are synchronized. This is referred to as a phase encoding gradient and the direction in which it is applied is denoted the phase encoding direction.
3.
Applying a gradient during acquisition of the signals will make nuclei at different positions emit signals with different frequencies. Such gradient is referred to as a readout gradient and the direction in which it is applied is denoted the frequency encoding direction.
Thus, by sampling the emitted signals and analyzing their phase and frequency spectrum, information about nuclei from different parts of the subject can be obtained. However, all information required to generate an image cannot be contained within just one sampled signal. Thus, the combination of gradients and RF pulses must be repeated many times, changing the phase encoding gradient slightly for each repetition, in order to obtain the information necessary to generate an image. Such combination of repeated gradients and RF pulses is denoted a pulse sequence and can be configured in a large number of ways in order to enhance the obtained image for different purposes. The execution time of a clinical pulse sequence typically ranges between 1 and 10 min.
When a pulse sequence is executed, the sampled signals together constitute a spatial frequency representation of the object, which can later be Fourier transformed into a real visible image. Such frequency representation is called a k-space image.
Gradient Echoes and Spin Echoes
As described earlier, nuclei that are perturbed by an external RF pulse will respond by generating an RF signal of their own (i.e., a FID). In order to use this signal for image formation it is necessary to first subject the nuclei to a series of magnetic field gradients, as signals originating from different parts of the tissue would otherwise not be distinguishable. Since these gradients have a duration in the order of a few milliseconds, the acquisition of signal is usually delayed from the RF pulse, leaving enough time for the gradients to be applied. This type of acquired signals is referred to as echoes, of which the two most commonly used types are the gradient echo and the spin echo.
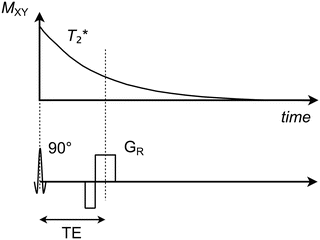
The gradient echo is the simplest type of echo as it basically only involves an excitation RF pulse followed by a set of gradients applied directly on the FID signal. These gradients can be configured in a variety of ways, although they are all characterized by having a final readout gradient during which the actual echo signal is retrieved (Fig. 1.6). The time that arises between the RF pulse and the echo is denoted the echo time (TE), which can be set arbitrarily with respect to the minimum time required for the gradients to apply. However, it should be noted that since the FID signal decays at the relatively fast T 2* speed, the echo time must be kept short (typically 2–20 ms) in order for the echo amplitude not to be unreasonably low. As a consequence, the echo time can be used to adjust how much impact the T 2* of the tissue will have on the echo amplitude and thereby also on the contrast within the resulting image.
Get Clinical Tree app for offline access

Fig. 1.6
Transverse magnetization (M XY




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree