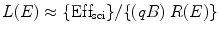(1)
Radiation Monitoring Devices Research Nuclear Medicine, Water town, Massachusetts, USA
5.1 Introduction
5.10.1 Photoelectric Effect
5.10.2 Compton Effect
5.10.3 Pair Production
5.11 Ionization Losses
5.14 Solid-State Detector
Abstract
The radiation detectors are mainly divided into two large groups: (1) scintillation detectors and (2) semiconductor diodes. The first one can detect high-energy radiation through generation of light that can subsequently be registered by a photodetector, either a photomultiplier tube (PMT) or an avalanche photodiode (APD) [1–7]. The PMT or APD converts the light signal into electrical signal, which is ultimately measured. The main advantage of these detectors is their large detection volume [8, 9].
5.1 Introduction
The radiation detectors are mainly divided into two large groups: (1) scintillation detectors and (2) semiconductor diodes. The first one can detect high-energy radiation through generation of light that can subsequently be registered by a photodetector, either a photomultiplier tube (PMT) or an avalanche photodiode (APD) [1–7]. The PMT or APD converts the light signal into electrical signal, which is ultimately measured. The main advantage of these detectors is their large detection volume [8, 9].
The key requirement for best efficiency of a scintillator is that it should be transparent to its own radiation. Therefore, in order to optimize the performance of a scintillator, it is important that nearly all light that is created within the scintillator be received by the subsequent photodetector. A good scintillator has emission band gaps that do not overlap with the optical absorption band gaps because an overlap will cause excessive self-absorption of light in the scintillator. Therefore, the material is chosen in such a way that the radiative component of recombination dominates over non-radiative components [10].
The optical properties of a scintillator do not depend on the lattice orientation, but the presence of significant impurities around grain boundaries severely affects the optical properties. In particular, the image quality of a gamma camera is seen to degrade when light output across a grain boundary of the scintillator is affected.
The incoming photons received by the photocathode are influenced by the refractive index (RI) of the materials of the imaging system. It is to be noted that the RI of the materials of the imaging system should match each other. In a case where they do not match with the light coming out of the surface of the scintillator and the entering surface material of the photocathode, one can notice that one component of light is being reflected and the other component is being refracted at the interface. From our experimental observations, we have found that the RI of most of the scintillating materials is between 1.44 and 2.20, and the RIs of air, glass, and quartz that exist in the pathway of the outgoing light are ~1, 1.5–1.7, and ~1.47, respectively. In our present medical imaging system, the light that comes out of the scintillator passes through air before entering into the photocathode, with an envelope made out of either glass or quartz. So we should expect some loss of light before it is received by the photocathode. Additional light losses can occur inside the scintillator itself (internal reflection, and in case of a single crystal, it depends on the crystal structure too). However, polished scintillator surface can minimize the loss of output light.
Total internal reflection of light occurs in a material at a critical angle (θ c) or Brewster’s angle and can be expressed mathematically as
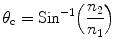
where n 1 and n 2 are the refractive indices of the material in which light originates (scintillator) and the material across the interface (air), respectively. It would be a good idea to use a good diffuse reflector to return the light into the crystal when the angle of incidence is less than the critical angle.
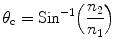
(5.1)
The second category of detector is semiconductor PN junction reverse-biased diodes where the absorbed radiation creates electron–hole (e–h) pairs. By applying electric field across the PN junction, the e–h pairs are separated and a direct electrical signal is produced [11]. Recently, silicon PIN (I stands for insulator) diodes are used as nuclear radiation detectors and have been found to be more efficient than PN junction diodes. The PIN diode detector, where I stands for insulating layer in between the P and N junctions, detects radiation by generating a transient photocurrent when the incoming radiation is absorbed in the insulating (I) layer. In practice, I region of the PIN device is kept large to maximize the photocurrent.
When the PIN device is exposed to the nuclear radiation, the energy quanta, which are absorbed by the elements of the lattice structure, produce electron–hole pairs provided the energy quanta are larger or equal to the band gap energy of the material. Now when the device is reverse biased, I layer is depleted of free carriers and electrons are swept to P layer and the holes are swept to the N layer, respectively. The most important criterion of PIN detector is that they are not restricted to use at low temperature like PN junction devices.
Semiconductor radiation detectors (SRD) play an important role in radiation instrumentation. Being small in size, SRD have many advantages as nuclear detectors such as (1) they have outstanding energy resolution in nuclear spectroscopy, (2) they can be pixelated easily for high spatial resolution, and (3) they can be integrated easily with readout electronics. Advancement in the semiconductor industry has made silicon as one of the most popular material for radiation detectors in medicine with applications in diagnostic and cancer treatment [12].
Extensive studies of both groups of detectors revealed their pros and cons [13]. The diodes typically suffer from inadequate electron–hole (e–h) production and loss of e–h pairs during collection due to the imperfection of the device. The most common semiconductor materials used for radiation detection are lithium-doped silicon (SiLi) and germanium (Ge). Both of them require high voltage typically on the order of kilovolts to maximize the charge collection and to increase the drift velocity. In case of scintillators, the efficiency of converting the high-energy radiation into light is typically on the order of 10–12 %.
Recently some workers are working on some direct band gap semiconductors like CdS and ZnO doped with donors in a reducing atmosphere [14]. The discovery of epitaxy and its application in device manufacturing has made possible the existence of lattice-matched multilayer devices with two alternating materials like InP/Ga0.47In0.53 or Al x Ga1−x As/ GaAs. Upon interaction with the ionizing radiation, the created electrons and holes will quickly diffuse into InGaAs well and will recombine. The difference in band gap energies will ensure that all the light absorbed in InGaAs and InP will remain transparent to emitted photons [15, 16]. It is believed that these devices might be the most promising and efficient semiconductor detectors in medical science and will replace silicon-based devices in the near future.
5.2 Working Principle of the Detectors Used in Nuclear Medicine
The detection of ionizing radiation by scintillation light produced by certain materials is one of the oldest and useful methods adopted in nuclear medicine even today. The material in the form of single crystal or in the form of a polycrystalline film deposited either by thin (vacuum evaporation, hot-wall epitaxy, chemical vapor deposition process, or sputtering) or thick film (screen printing) [17] that produces light on being absorbed by ionizing radiation is called a scintillator.
The scintillation or the flashlight effect persists as long as the radiation energy is being absorbed. According to some experts, scintillation phenomenon can be described as the phenomenon of luminescence in transparent solids, fluids, or gases originating at the propagation of ionizing radiation through them [18, 19]. However, some critics have distinguished the phenomenon of luminescence and scintillation. According to their conceptions, scintillation is the energy loss of ionizing radiation through matter, whereas luminescence is the results from the radiative relaxation of an active ion of the material after it is being excited between its fundamental state and excited energy levels by an electrostatic discharge or a pulse of light.
As a matter of fact, luminescence can be subgrouped into four categories, namely, (1) excitation luminescence, where the ionization/excitation by radiation can create e–h pairs or bound e–h pairs called excitons, a vivid example of this type of luminescence is bismuth germanate (BGO, Bi4Ge3O12); (2) the dopant luminescence, where radiative recombination of self-trapped excitations occurs at dopant ions, as we found in gadolinium oxysulfide (GOS:Ce,Gd2O2S); (3) charge transfer luminescence, where excitation due to charge transfer is different for initial and final states and the selection rules for electromagnetic transition are loosened, as in the case of yttrium aluminum garnet (YAG:Yb,Y3Al5O12); or (4) core valence luminescence, where after excitation of the core-valence electron, an electron in the valence band recombines with the resultant hole radiatively, as we found in the case of barium fluoride (BaF2), calcium fluoride (CsF), and lithium fluoride (LiF).
However, according to some observers, scintillators are energy converters that convert the incident energetic photon (UV, X-ray, or gamma ray) into a number of photons of much lower energy having longer wavelengths in the visible or near-visible range. According to them, scintillators are transparent dielectric media where luminescence is induced by ionizing radiation. Some of these luminescence centers are cations or anionic complexes of the lattice or doping ions such as Ce3+.
There are wide varieties of materials that have shown scintillation properties when properly excited with radiation light [20]. These materials can be grouped into three main categories: (a) organic, (b) inorganic, and (c) solid–state scintillators. The ideal scintillating materials should possess the following properties:
(a)
Conversion of the kinetic energy of the charged particles into highly efficient scintillation light.
(b)
The medium should be transparent to the wavelength of the scintillation light so that minimum amount of light will be absorbed or lost during transition.
(c)
The conversion should be linear and the material should have good optical quality with refractive index comparable to glass (~1.5).
(d)
The decay time of the induced luminescence should be short.
The general idea behind the scintillation process is the conversion of energy of an incident gamma quantum or particle into great many low-energy photons. The ionization event put the scintillator in a state of nonequilibrium situation. As time goes on, the scintillator begins to relax toward a new equilibrium situation. During relaxation, a multitude of elementary processes such as creation of primary electronic excitation occur. As a result of this excitation, one can expect an avalanche of secondary excitations including electrons, holes, photons, and plasmons. In addition to those events, electronic excitations will also produce thermalized electron–hole (e–h) pairs and low-energy excitations which ultimately transform into light photons, that is, scintillation [20–22].
Electrons and holes produced by ionizing radiation have several ways to be involved in scintillation process after thermalization. The simplest one is the direct radiative recombination of free thermalized electrons in the conduction band with holes from the valence band or from outer electronic shells. The excitation luminescence is efficiently quenched causing a sensitization of luminescence of the activating ions in presence of impurity centers or activating ions. In case of heavily doped or self-activated scintillators like CeF3, the direct excitation of the activation centers by ionizing radiation provides an important contribution to the scintillation.
5.3 Organic Scintillators
Organic scintillators are aromatic hydrocarbon compounds containing a benzene cycle. In organic scintillators, the mechanism of light emission is a molecular effect. The most distinguishing feature of an organic scintillator is their very rapid decay time. It proceeds through excitation of molecular levels in a primary fluorescent material, which emits bands of ultraviolet (UV) light during de-excitation. The UV light is absorbed in most organic materials with an absorption length of few mm.
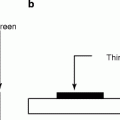
The organic scintillators have low Z value; as a result, the organic scintillators do not show photo-peak and give rise to a Compton continuum in their γ-ray pulse height spectrum. However, recent developments in organic scintillators have made to add high Z-elements. Unfortunately, the addition of high Z-elements decreases the light output. A typical energy band diagram of an organic scintillator is shown in Fig. 5.1 with the distinguishing features of spin singlet state with that of a triplet state. The states above the singlet ground state S0 are excited states. In case of triplet state, the ground state is T0 and above that all the remaining states are excited states. Being hit by radiation light, the scintillator material emits light, which arises from the transitions made by the free valence electrons of the molecules. These delocalized electrons are not associated with any particular atom in a molecule and they occupy the π-molecular orbitals [23, 24].
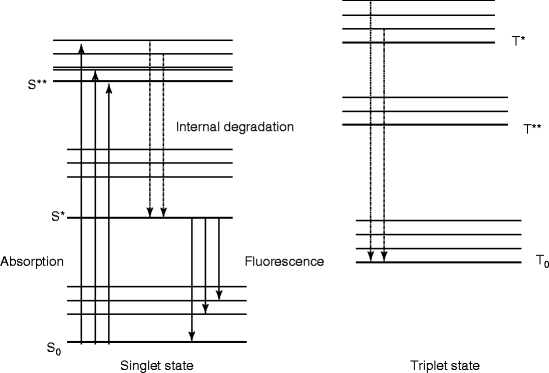

Fig. 5.1
The energy level diagram of an organic scintillator molecule
From our experimental observations we know that stilbene has lower scintillation property than anthracene, but it is preferred in those situations where pulse shape discrimination is to be used to distinguish among scintillations induced by charged particles and electrons. On the other hand, naphthalene in ethyl alcohol has also been used as organic scintillators [25].
The plastic scintillators like NE102A and NE10 have the advantage that they can be produced in a variety of shapes according to the application needs. Most frequently they are used as rectangular plates from 0.1 up to 30.0 mm and area from a few mm2 to several mm2. Some of these materials are used in the detection of β particles. Unfortunately, the devices made out of these materials are fragile and difficult to obtain in large sizes.
There are some other organic materials that have been used as scintillators such as (1) PPF2, 7-diphenyl-9,9-dipropyl fluorine; (2) d-amyl-PPF, 2,7-bis(4-t-amyl phenyl)-9,9-dipropyl fluorine; and (3) d-CH3O-PPF 2,7-bis(4-methoxy phenyl)-9,9-dipropyl fluorine [26]. Synthesized methyl and/or methoxy substituted 1,3-diphenyl-2-pyrazolines in benzene [27].
Sometime organic materials are dissolved and sealed in a tube for better handling as a detector. These liquid scintillators are used for measuring β emitters; particularly they are classified as weak β emitters. The sample is dissolved or suspended in an organic chemical, which fluoresce when acted by ionizing radiation [28, 29]. The radiation is then converted into pulses and detected by photomultiplier tube. Organic scintillators are generally used for direct detection of β particles (fast electrons) or alphas (positive ions), fast neutrons through proton recoil process. Table 5.1 shows some of the basic properties of organic scintillators.
Table 5.1
Properties of some organic scintillators
Properties | Anthracene | Polysyrene | Stilbene | NE 102 | NE 10 | NE224 liquid | NE316 Sn-loaded liquid |
|---|---|---|---|---|---|---|---|
Density g/cm3 | 1.25 | 1.06 | 1.22 | 1.032 | 1.032 | 0.877 | 0.96 |
H to C ratio | 0.714 | 1.0 | 0.857 | 1.105 | 1.105 | ||
Emission spectrum (nm) | 448 | 430 | 400 | 425 | 437 | 425 | 425 |
Decay time constant (ns) | 31 | 2–3 | 3.5 | 2.5 | 3.3 | 2.6 | 4.0 |
Scintillation amplitude | 100 | 56 | 11 | 65 | 60 | 80 | 35 |
Main application | α, β, γ, and n | α, β, γ, and n | γ and n | α, β, γ, and n | γ and n | γ only | γ and X-rays |
Liquid scintillator counting (LSC) may be used to quantize alpha particles for a wide range of applications, such as environmental monitoring, nuclear fuel processing, and high-level waste management. Alpha-emitting radionuclides when quantitated by LSC generally produce a symmetrical peak around the energy maximum of the alpha particle, whereas in beta-emitting radionuclides, a beta emitter produces a continuous spectra from zero to energy maximum of the beta particle. As a matter of fact, LSC reduced the time required to analyze radioactive samples from hours to minute. For low-energy (soft) β emitters, LSC offers unmatched convenience and sensitivity. LSC detects radioactivity via the same type of light emission events, which are used in solid scintillators. The solvent portion of an LSC is about 60–90 % [30].
During the isolation of alpha-emitting radionuclides in nuclear fuel processing and other related processes, organic extraction techniques are employed to separate alpha-emitting radionuclides from one another, as well as from contaminating beta nuclides [31, 32]. Quenching agents are generally used to prepare samples that affect the resolution.
For organic scintillators such as anthracene, stilbene, and many of the commercially available liquid and plastic scintillators, the response of electrons is linear for particle energies above about 125 keV. The response of organic scintillators to charge particles can be expressed in terms of the fluorescent energy emitted per unit path length (dL/dx) and the specific energy loss for the charged particles (dE/dx). In absence of quenching, (dL/dx) = S (dE/dx), where S is the normal quenching efficiency, and the light output L = SE, where E is the energy output. The light output vs. photon energy of a typical liquid scintillator is shown in Fig. 5.2.
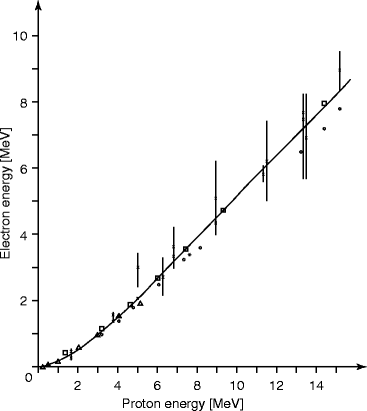

Fig. 5.2
The light output vs. photon energy for a liquid scintillator (NE-213) (Reprinted with permission, Maier and Nitschke)
5.4 Light Output in an Organic Scintillator
The organic scintillator is doped with a second fluorescent material, which is called wavelength shifter, to extract a light signal due to conversion of UV light into visible light. The second fluorescent substance is chosen in such a way that its absorption spectrum matched to the emission spectrum of the primary fluor, and its emission spectrum, adapted to the spectral dependence of the photocathode quantum efficiency [33].
These two active fluorescent materials are either dissolved in a suitable organic solvent (s) or mixed with a monomer of a material capable of polymerization. For organic scintillators, the differential light output (dL/dx) due the ionizing radiated light is related to the stopping power of the ionizing particle (dE/dx) which is known as Birks’ law [34], and mathematically we can express it as
![$$ {(\mathrm{ dL}/\mathrm{ dx})}=\{(\mathrm{ d}E/\mathrm{ d}x)\mathrm{ Ef}{{\mathrm{ f}}_{\mathrm{ sci}}}\}\{[1]/[1+qB\;(\mathrm{ d}E/\mathrm{ d}x)]\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00052.gif)
where Effsci is the efficiency of the scintillator, B is Birks’ parameter, and q is the quenching parameter. The qB in Eq. 5.2 has saturation constant value between 0.01and 0.02 g/cm2 MeV. For fast electrons (dE/dx is small), the above equation transforms to
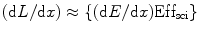
![$$ {(\mathrm{ dL}/\mathrm{ dx})}=\{(\mathrm{ d}E/\mathrm{ d}x)\mathrm{ Ef}{{\mathrm{ f}}_{\mathrm{ sci}}}\}\{[1]/[1+qB\;(\mathrm{ d}E/\mathrm{ d}x)]\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00052.gif)
(5.2)
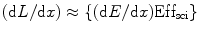
(5.3)
However, for alpha (α) particle, where (dE/dx) is large, the Eq. 4.2 can be written as
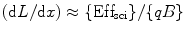
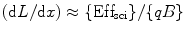
(5.4)
It has been found from the experimental studies that liquid and plastic scintillators show luminescence quenching which is wholly responsible for the interaction between the excited solvent and the quencher, which competes with the energy transfer process from the solvent to the fluor (fluorescent solute). The advantage of studying energy transfer and quenching in plastic scintillators is that the rigidity of the medium hinders molecular diffusion and collision.
5.4.1 Fluorescence and Phosphorescence
Both the fluorescence and phosphorescence phenomena occur due to de-excitation of electrons. When a fluorescence material is exposed to thermal or radiation energy, it produces high-energy photons that collide with electrons in the material causing them to be excited and jump to a higher energy level. The electrons in the excited states have the same spin as they had in the ground state. However, the electrons in the excited states are not stable and they release energy in the form of light and are de-excited. When they are de-excited, they come back to the ground state. Phosphorescence is similar to fluorescence except that the light emission continues even after the radiation energy or the thermal energy is removed.
The other way to distinguish fluorescence and phosphorescence is primarily on the basis of the duration of the afterglow—a slow decay of luminescence being called phosphorescence. However, in scattering (Raman and Rayleigh) of light, there is no absorption of light. Rayleigh and Raman scattered light following oscillation of an induced dipole moment consists of two polarization components that are aligned perpendicular and parallel to the scattering plane (depolarization) [35–37].
Afterglow can be attributed due to the following reasons: (1) natural, (2) metastable states or traps (impurities, defects, etc.), and (3) speed of energy transfer and number of luminescence centers. Besides pulse shape discrimination techniques, the knowledge of radioluminescence decay curves is, in itself, the fundamental importance in radiation physics and chemistry, and it enables to get information on the nature of the basic processes induced by nuclear particles in organic media [37].
5.5 Kinetics of Quenching in Organic Scintillators
The organic scintillator under study consists of solute (polystyrene), fluor (F = diphenylanthracene, DPA), solvent (S), and a dopant which is a quencher (Q = chloro- or bromo-substituted organic compounds). In the ternary matrix, the concentration of the fluor is kept fixed, while the concentration of the dopant is a variable quantity. Let the ternary matrix be perturbed by a flux of beta (β) ray from a strontium (Sr90) source. The luminescence quenching in the liquid scintillator is attributed to the interaction between the excited solvent and the quencher, and it competes with the energy transfer process from the solvent to the fluor (fluorescent solute). One of the advantages of studying quenching in plastic scintillators is that the rigidity of the medium hinders molecular diffusion and collision.
The theoretical values for the solvent quenching constant (α) and the solute quenching constant (β) can be expressed mathematically as [38]
![$$ \alpha ={k_{\mathrm{ Q}}}/({k_{\mathrm{ e}}}+{k_{\mathrm{ i}}}+{k_{\mathrm{ s}}}+{k_{\mathrm{ F}}}[\mathrm{ F}]) $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00056.gif)
![$$ \beta ={{k^{\prime}}_{\mathrm{ Q}}}/\left( {{{{k^{\prime}}}_{\mathrm{ e}}}+{{{k^{\prime}}}_{\mathrm{ i}}}+{{{k^{\prime}}}_{\mathrm{ s}}}} \right.[\mathrm{ F}]) $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00057.gif)
![$$ \alpha ={k_{\mathrm{ Q}}}/({k_{\mathrm{ e}}}+{k_{\mathrm{ i}}}+{k_{\mathrm{ s}}}+{k_{\mathrm{ F}}}[\mathrm{ F}]) $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00056.gif)
(5.6)
![$$ \beta ={{k^{\prime}}_{\mathrm{ Q}}}/\left( {{{{k^{\prime}}}_{\mathrm{ e}}}+{{{k^{\prime}}}_{\mathrm{ i}}}+{{{k^{\prime}}}_{\mathrm{ s}}}} \right.[\mathrm{ F}]) $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00057.gif)
(5.7)
And the quantum efficiency of energy transfer from S* to F is ϕET and can be presented mathematically as
![$$ {\varphi_{\mathrm{ ET}}}={k_{\mathrm{ F}}}[\mathrm{ F}]/({k_{\mathrm{ e}}}+{k_{\mathrm{ i}}}+{k_{\mathrm{ s}}}+{k_{\mathrm{ ET}}}[\mathrm{ F}]+{k_{\mathrm{ Q}}}[\mathrm{ Q}]) $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00058.gif)
where the quantities k e, k i, k s, k ET, and k Q are rate constants for emission, internal quenching, self-quenching, energy transfer to the fluor, and quenching by the quencher for excited solvent S*, respectively. Similarly, the quantities with prime are the rate constants for the excited fluor F*. The square brackets indicate the concentration in mole/liter (L).
![$$ {\varphi_{\mathrm{ ET}}}={k_{\mathrm{ F}}}[\mathrm{ F}]/({k_{\mathrm{ e}}}+{k_{\mathrm{ i}}}+{k_{\mathrm{ s}}}+{k_{\mathrm{ ET}}}[\mathrm{ F}]+{k_{\mathrm{ Q}}}[\mathrm{ Q}]) $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00058.gif)
(5.8)
Again the solvent and the solute quenching constants can be deducted mathematically as
![$$ \alpha [\mathrm{ Q}]=\{({\tau_{\mathrm{ S}_0}}/{\tau_{\mathrm{ S}}})-1)\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00059.gif)
![$$ \beta [Q]=\{({\tau_{{\mathrm{ F}_0}}}/{\tau_{\mathrm{ F}}})-1)\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ000510.gif)
where τ S and τ F are the mean lifetime of the excited state of the solvent (S*) and that of the fluor (F*) when the quenching reagent is present. τ S0 and τ F0 are the mean lifetime of the excited state of the solvent (S*) and that of the fluor (F*) when the quenching reagent is absent. Now we can find out the values of the α[Q] and β[Q] presented in Eqs. 5.9 and 5.10 from the slope of the straight line fitted to the least-squares method to the plots of 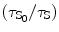 and
and 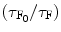 .
.
![$$ \alpha [\mathrm{ Q}]=\{({\tau_{\mathrm{ S}_0}}/{\tau_{\mathrm{ S}}})-1)\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ00059.gif)
(5.9)
![$$ \beta [Q]=\{({\tau_{{\mathrm{ F}_0}}}/{\tau_{\mathrm{ F}}})-1)\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ000510.gif)
(5.10)
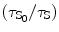 and
and 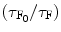 .
.Experimental studies show that fluorescence quenching is dependent on the solvent, the quencher, and the nature of the substituent. The heavy atom quencher increases fluorescence, which has been attributed to internal or external spin–orbit coupling effects. These effects are seen to increase the probability of singlet–triplet absorption and decrease the lifetime and quantum yield of phophorescence [39].
Further studies on fluorescence of the organic scintillators show higher degree of solvent quenching in ionizing radiation compared to UV exposure. The most possible cause is thought to be due to the larger amount of energy transfer and highly excited states of the solvent (such as polystyrene). It is also inferred that the energy transfer from the excited state of fluor to the triplet state of quencher is responsible for solute quenching.
5.5.1 Mean Lifetime of the Organic Scintillator
New interest for organic scintillators arose when it was recognized that the emission decay involves a slow component, which depends on the ionizing power of the nuclear radiation. The phenomenon was soon applied to particle discrimination. The origin of the slow component results from triplet interaction leading to a singlet state. However, a part of these states is produced very rapidly and gives rise to prompt emission intensity, which decays exponentially with a time constant identical to the mean lifetime τ [40]. Mathematically, the mean lifetime (τ) of an excited state can be written following Stern–Volmer kinetic relation as
![$$ ({\tau_0}/\tau )=1+\beta {\tau_0}[\mathrm{ Q}\;\mathrm{ or}\;\mathrm{ S}] $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ000511.gif)
where τ 0 is the lifetime of the excited state in absence of quencher Q and S stands for solute.
![$$ ({\tau_0}/\tau )=1+\beta {\tau_0}[\mathrm{ Q}\;\mathrm{ or}\;\mathrm{ S}] $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ000511.gif)
(5.11)
And the triplet lifetime τ T is defined as
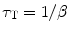
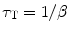
(5.12)
Again the intensity (I) of radiation light at time t and the initial intensity (I 0) at time t = 0 can be correlated as
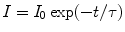
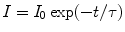
(5.13)
5.6 Scintillation Efficiency of an Organic Scintillator
The quantum efficiency (QE) of fluorescence is defined as the fraction of all incident particle energy, which is converted into visible light. Unfortunately, all the incident particles are not converted into visible light but ended into heat due to quenching. On the other hand, the quantum efficiency of an activated scintillator is very much dependent on the ratio of the band gap of the material to the energy of the activator in the radiating state. It is also related to the position of its ground and excited states to the valence and conduction bands, respectively [41, 42]. The change in photon energy causes a shift of the fluorescence spectrum to longer wavelength, relative to the absorption spectrum, which is referred to as Stokes shift.
From the definition of the quantum efficiency of an organic scintillator (solute + solvent + quencher (if there is any)), we can write the number of photons absorbed per volume per unit time (ϕ pa) as [43]
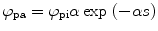
where ϕ pi is the number of photons incident on the cell containing the liquid scintillator, α is the optical absorption coefficient of the solvent, and s is distance within the solution from the front window of the cell.
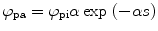
(5.14)
Let us consider that the liquid scintillator within the cell is perturbed by a radiation light and the output signal is received by a photomultiplier tube (PMT). As a result of the incoming energy flux, we will notice a current (I s) in the PMT when viewing solvent emission under optical excitation and a PMT current (I c) when viewing solvent emission under C14 excitation conditions. The ratio between the two currents can be expressed mathematically as:
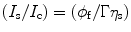
where φ f is the fluorescence quantum yield of the solvent, η s is the scintillation efficiency, and Γ is equal to
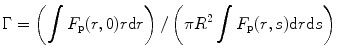
where F p is the fraction of the photons received by the photomultiplier tube (PMT), r is the radial distance away from the axis of the cylinder, and R is the radius of the exciting radiation beam. Now, if we assume that there is no emission from the back of the cell, we can write the scintillation efficiency as
![$$ {\eta_{\mathrm{ s}}}=\left\{ {[\{({I_{\mathrm{ c}}}{\phi_{\mathrm{ f}}})/{I_{\mathrm{ s}}}\}{I_0}\alpha ]/\pi {R^2}} \right\}\left\{ {\int {(\exp (-\alpha s){F_{\mathrm{ p}}}(r,s)r\mathrm{ d}r\mathrm{ d}s)} /\int {({F_{\mathrm{ p}}}(r,s)r\mathrm{ d}r\mathrm{ d}s)} } \right\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ000517.gif)
where the integral extends from r = 0 to r = R. The mathematical expression of Eq. 5.17 is established on the assumption that the radiation beam is homogeneous over R. For extreme case when the absorption coefficient α is very large and the absorption is confined to the immediate vicinity of the front window, the above expression (5.17) transforms to
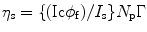
where N p is the total number of photons absorbed per unit time.
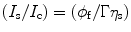
(5.15)
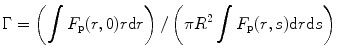
(5.16)
![$$ {\eta_{\mathrm{ s}}}=\left\{ {[\{({I_{\mathrm{ c}}}{\phi_{\mathrm{ f}}})/{I_{\mathrm{ s}}}\}{I_0}\alpha ]/\pi {R^2}} \right\}\left\{ {\int {(\exp (-\alpha s){F_{\mathrm{ p}}}(r,s)r\mathrm{ d}r\mathrm{ d}s)} /\int {({F_{\mathrm{ p}}}(r,s)r\mathrm{ d}r\mathrm{ d}s)} } \right\} $$](/wp-content/uploads/2017/03/A308734_1_En_5_Chapter_Equ000517.gif)
(5.17)
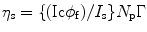
(5.18)
5.7 Structural and Electronic Properties of Scintillators
The structural and electronic properties of organic, inorganic, and ionic materials are important for the selection of a detector material for medical imaging [44–47]. A scintillator can be considered as essentially a photon conversion device. The most important similarity between ordinary luminescence and scintillation is in the role played by so-called luminescence centers that is generally created by an appropriately chosen dopant ion or activator. The ideal materials used for scintillators in medical imaging system should have high density, high effective number, high luminous efficiency, chemical stability, short decay time, no (or minimum) afterglow, good spectral match to photodetectors, and cost–effective. But in reality, it is hard to find any single material, which will possess all these properties. Thus, there is a need to compromise choosing from available materials that will be most suitable for a particular application such as planar X-ray, X-ray CT, SPECT, or PET.
Modeling [48, 49] a scintillator material in terms of structural and electronic properties means studies of its atomic structure as a function of density [50] and electron excitations vs. structure [51].
Scintillators are used as radiation detectors for X-rays, gamma (γ) rays, electrons, neutrons, alpha (α) and beta (β) particles, and neutrinos. Efficient detection of these particles (through radiation) depends on how well and how quickly they lose their energy in the detector. One of the most important properties of a scintillating material is its stopping power, which depends not only on the atomic weight (Z-factor) of the material but also on the density of the material [52]. As for example, cadmium tungstate (CdWO4, CWO, density 7.9 g/mL) produces higher light output than bismuth germanate (BGO, Bi4Ge3O12 density 7.19 g/mL) because of its higher density and atomic weight than BGO. Density and atomic weight are therefore important factors that are used to assess the effectiveness of a scintillator (scintillating material).
High density in scintillating materials is an advantage in applications where a compact high-efficiency counter is required. In other words, we can say that the detection efficiency (or γ-ray stopping power) of a scintillator depends on the density of the material [53]. Bismuth germanate (BGO, Bi4Ge3O12) and lutetium oxyorthosilicate (LSO, Lu2SiO5:Ce) have dominated the field of positron emission tomography (PET) because their high density and high atomic number (Z) imply a short attenuation length and consequently high spatial resolution. On the other hand, low-density organic scintillators have made them inefficient for detecting photons [54, 55].
Structural properties of a scintillator (radiation detector) are important because they affect a material’s absorption and emission characteristics and its response to heat, pressure, and other external and internal forces [56]. A systematic study of several hundred inorganic crystal structures on the basis of electronic structure calculations reveals that subgroup of more than 3,000 entries of crystals that contain one or more of the elements like mercury (Hg), thallium (Tl), lead (Pb), or bismuth (Bi,) have a Bravais lattice that is either cubic (Γc), orthorhombic (Γo), tetragonal primitive (Γq), or hexagonal (Γh).
The size of the energy gap between the empty and filled electron states greatly influences the frequency of light emitted (a wider gap corresponds to a higher frequency of light) by a particular semiconductor. Recently, there are several technologies to alter the band gap of a semiconductor. These are known as substrate engineering, or strain engineering, where the host semiconductor is mixed with another semiconductor having different band gap energy (e.g., Si1−x Ge x , implanting germanium into silicon). The strain engineering increases the mobility of charge carriers of an engineered semiconductor [57, 58].
Small band gap materials are not efficient scintillators, because when the emission energy is greater than the band gap of the material, the emitted photons are absorbed by the crystal (host lattice) itself and never exit the crystal. Moreover, due to photoionization the electron in the excited state is injected back into conduction band by thermal activation. For example, in Lu2O3:Ce all the Ce+35d1 states are located within the conduction band of the solid and the cerium luminescence is totally quenched [59].
The crystal structure (e.g., cubic, monoclinic, or orthorhombic) determines the internal loss of light, which ultimately affects the light output of the scintillator. Most scintillators are made in such a way that they produce light in the visible region of the electromagnetic (EM) spectrum. Since the photons produced in the scintillator have to be guided to the photodetector, they must travel through the material without significant attenuation. Attenuation of photons causes loss of output light and information, besides induction of nonlinearity in the detector response. Unfortunately, most of the efficient scintillators produce ultraviolet photons with short attenuation length and therefore quickly get absorbed without producing sufficient information.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree