1.2.1 Tomography

Consider a simple, cylindrical object that is being imaged. The tomographic system (e.g., a SPECT or CT system) acquires “projection” data about the object (► Fig. 1.1). To first order, the data acquired at each location along the projection can be assumed to have originated along a ray intersecting at right angles to the detection device and extending back through the object. A complete set of projection data is acquired at evenly spaced angular intervals about the object. Depending on the particular tomographic imaging modality, a complete set may be considered a rotation over 180 or 360 degrees, as discussed in this chapter. The tomographic data set for a volume will consist of projection data acquired for a series of parallel transverse planes or slices through the object. Although the acquisition of parallel rays within a projection may be reasonable for some applications and certainly provides a simple conceptual model, in many cases, it may be more efficient to acquire the data in either a fan-beam or cone-beam geometry. A complete set of projections acquired in fan-beam geometry can be reformatted into one consisting of parallel beams and thus can be considered to be equivalent. However, cone-beam geometries can provide some technical challenges, as discussed in this chapter.

Each one-dimensional (1D) projection can be stacked to form a two-dimensional (2D) image, where displacement across the projection is on the x-axis and the angle of orientation of that particular projection is on the y-axis (► Fig. 1.2). This representation of a complete set of projection data associated with a single slice through the object is known as the “sinogram” since such a representation of a point source results in a sine wave rotated 90 degrees. For a volume of data, each transverse slice would be represented by its own sinogram. The contour of a sinogram should normally be smooth and continuous. A break in the contour indicates patient motion (see ► Fig. 5.8 in Chapter 5).

The fundamental challenge of tomographic reconstruction is to estimate the internal structures of the object, given the set of projection data acquired about the object. With parallel-ray projection data, the events detected at a certain locus along the projection can be back projected across the object, assuming that the events must have originated along that ray (► Fig. 1.2). If this “simple back projection” is applied to all locations for all projections, the resultant reconstruction will provide a crude reconstruction of the data that is blurred considerably by streak artifacts. This is caused by the uneven sampling of frequency data, where high frequencies are sampled less often than low frequencies. Applying a “ramp filter,” that is, one that weights the frequency components in a linear fashion, compensates for these streak artifacts but also leads to amplification of high-frequency noise in the reconstructed image. Therefore, a windowing filter (e.g., Butterworth, Hanning, Hamming, Shepp-Logan) is typically applied. A cutoff frequency is defined for the windowing function depending on the imaging task that effectively smooths the high-frequency noise while maintaining image quality with acceptable spatial resolution. This approach, referred to as filtered back projection, is relatively simple, fast, and robust and continues to be the standard reconstruction method for CT.

An alternative to filtered back projection is iterative reconstruction. In this approach, an initial guess of the object is assumed (e.g., that the object is uniform). From this initial guess, a set of projection data is generated using an a priori model of the imaging modality (► Fig. 1.3). This set of generated projections is compared to the set of acquired (real) projections. The differences between the generated and real projections are back projected and added to the original guess, providing an update. This series of steps is repeated or “iterated” until an acceptable solution is reached. In determining the difference between the two sets of projections, a specific statistical criterion is applied. One commonly used criterion for iterative reconstruction is maximum likelihood. As a result, the reconstructed image is that which is most likely, in a statistical sense, to have led to the given set of projections. In addition, an optimization algorithm, such as expectation maximization, is utilized. As a result, the maximum likelihood expectation maximization (MLEM) algorithm is commonly used for the iterative reconstruction of medical image data.

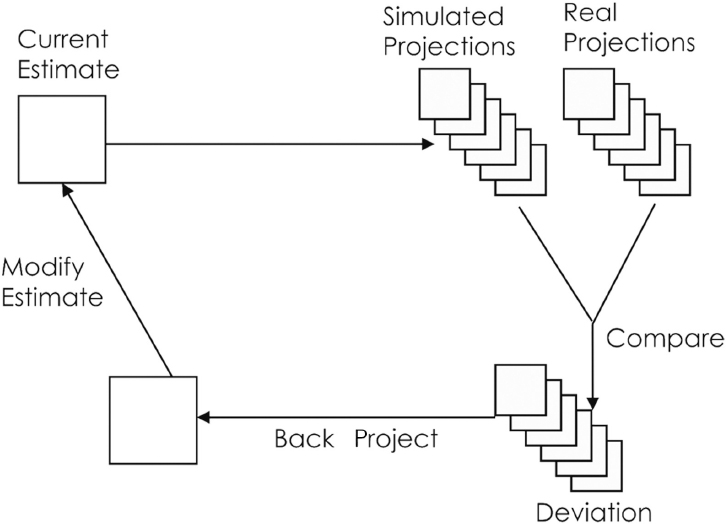
Iterative reconstructions can lead to improvements in image quality relative to filtered back projection. In the first place, as the method does not directly rely on back projection, the streak artifacts that can be encountered in filtered back projection are minimized considerably. Also, the Poisson statistical nature of the acquired projection data is specifically modeled into the MLEM algorithm. In addition, the iterative approach allows the incorporation of knowledge of the imaging process into the reconstruction process. These considerations can be incorporated directly into the model that is used for first generating the estimated projections from the current guess of the object being imaged and then reprojecting the difference between the two projection sets. This can include knowledge of photon attenuation, scattering within the patient, or the variation of spatial resolution across the field of view. This is in contrast to filtered back projection with its rather naive assumption that the data can be uniformly spread across the entire breadth of the patient. As a result, iterative reconstruction typically provides images that appear less noisy with fewer streak artifacts with the potential for higher spatial resolution. An example of streak artifact is shown in ► Fig. 8.4 in Chapter 8.

The MLEM can take tens of iterations, perhaps as many as 50 or 100, before obtaining an acceptable image. In general, the image will become sharper with more iterations but also noisier. In addition, acquiring many iterations can be time consuming, particularly for large data sets. Several approaches can be used to improve the image quality when more iterations are used or to reach an acceptable image with fewer iterations. A simple approach to reducing the image noise is to apply a postreconstruction regularization filter. The amount of smoothing applied can be varied depending on the acquisition modality and imaging task at hand.

In the traditional MLEM algorithm, the entire set of projections must be processed prior to generating an updated guess of the object. One way of obtaining an acceptable image with fewer iterations is to divide the set of projections into subsets of projections that are uniformly distributed about the patient. For example, assume that 100 projections (numbered 1 through 100) have been acquired about the patient and we want to divide this into 10 subsets. The first subset might contain projections 1, 11, 21, 31, …, 81, 91. After applying the iterative algorithm to these 10 projections, the initial guess is updated. The next subset may contain projections 2, 12, 32 82, 92, and again updating the guess. After processing the full set of projections with 10 subsets, the initial guess has already been updated 10 times. As a result, fewer iterations are typically needed. The most commonly used algorithm for this approach is referred to as ordered subset expectation maximization (OSEM).

A rule of thumb indicates that OSEM yields similar image quality as MLEM when the product of the number of subsets and the number of iterations with OSEM equals the total number of iterations in MLEM. For example, OSEM reconstruction with 16 subsets and 3 iterations yields a similar image quality to MLEM with 48 iterations. It should be noted that processing more subsets does not take additional time. It only changes the order with which the data are processed. As a result, the ability to significantly reduce the number of iterations, in turn, leads to a substantial reduction in processing time. If OSEM with 16 subsets and 3 iterations provides an acceptable alternative to MLEM with 48 iterations, the data are reconstructed about 16 times faster. The ability to provide reconstructed data in a timely fashion may be the determining factor in it being applied routinely in the clinic.

1.2.2 Single-Photon Emission Computed Tomography

The rotating gamma camera–the SPECT device most commonly used in the clinic–consists of one or often two standard Anger gamma camera detectors mounted onto a gantry that allows the cameras to rotate around the patient (► Fig. 1.4). Much of the following discussion assumes the use of parallel-hole collimation as this is most commonly used clinically. Focused collimation is also discussed briefly. The patient is administered a radiopharmaceutical. After an appropriate uptake period, the patient is placed on the imaging table and the SPECT acquisition begins. A static gamma camera image is acquired at a particular angle. The camera then rotates to the next position and a second projection image is acquired. This process continues until a full set of projections is acquired about the patient. For brain and whole-body SPECT, the set of projections is traditionally acquired over 360 degrees, whereas 180-degree rotation is more common for myocardial perfusion SPECT.

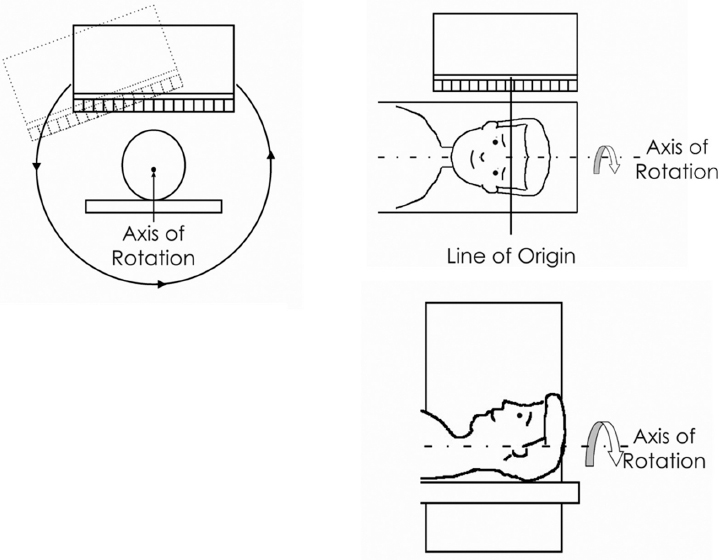
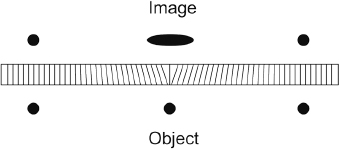
With parallel-hole collimation, one can assume, to first order, that the gamma ray resulting from a particular emission event along the “line of origin” intersects the camera crystal at the point of detection and extends back through the patient. Therefore, the acquired image can be considered a 2D projection image of the volume being imaged. Each horizontal row across the image represents the projection for that particular slice. Thus a single projection image represents a series of projections across all slices within the volume at a particular angle.

Although parallel-hole collimation is most commonly used in conjunction with the rotating gamma camera, focused collimation is sometimes used in special applications. Fan-beam or cone-beam collimation can provide enhanced sensitivity without sacrificing spatial resolution. This can be particularly useful when imaging a smaller region with a large field-of-view camera (► Fig. 1.5). For example, focused collimation has been applied to myocardial perfusion imaging, leading to three to four times the sensitivity with similar spatial resolution. The acquired projection data are subsequently reconstructed using either a fan-beam or a cone-beam algorithm. In modern cameras, the use of sophisticated robotics can assure that the region of interest is maintained in the center of the reconstructed field of view.

Pinhole collimation has also been applied successfully in SPECT of small objects. In this case, the detected event is assumed to have been emitted from the ray that intersects the crystal at the point of detection and passes through the pinhole back through the object. The use of very small pinhole apertures and significant image magnification can lead to outstanding spatial resolution. For example, in preclinical SPECT of small animals, apertures less than 1 mm have been used, leading to reconstructed spatial resolution of less than 1 mm. In this instance, the limited sensitivity of using such a small pinhole aperture is overcome by using multiple pinholes and maintaining a very short object-to-aperture distance. Since the sensitivity of a pinhole collimator varies as the inverse square of this distance, reasonable levels of sensitivity can be achieved with very short distances possible in small animal imaging. Although short object-to-aperture distances are not typically possible in clinical imaging, the use of multiple detectors with pinhole collimation has been applied to myocardial imaging, as discussed in this chapter.

1.2.3 Computed Tomography

CT, developed in the 1970s by Sir Godfrey Hounsfield, provides the ability to generate a cross-sectional representation of an object from a series of X-ray projections acquired about the object. This 3D representation greatly enhanced the image contrast by minimizing the ambiguity typically encountered in radiographs from over- and underlying tissues. The initial “first-generation” CT scanners required several minutes to acquire and reconstruct the data from a single slice. However, the technology developed quickly, and within just a few years, third-generation scanners could acquire data from a single slice on the order of a second. The introduction of helical and later multidetector CT allowed for the acquisition of an entire volume of the patient in less than a minute, thus making the modality truly 3D. CT could now provide high-resolution, high-quality anatomical representations of the patient in a matter of minutes. As a result, the clinical use of CT grew considerably from a few million CT procedures in the United States in 1985 to more than 80 million procedures by 2006. ¹

CT is a radiographic technique and thereby relies on the production of X-rays. As a result, the major components of the device are the X-ray tube and the detector matrix. Both of these are incorporated into a continuously rotating gantry that allows for the helical acquisition. The CT X-ray tube is essentially similar to a radiographic tube. Electrons are liberated from a heated cathode via thermionic emission and accelerated toward the tungsten anode. Upon striking the anode, a fraction of the electronic energy is converted into bremsstrahlung X-rays for imaging the patient. The number of electrons traversing the tube per second is characterized by the tube current, typically reported in milliamperes (mA). The number of X-rays produced is directly proportional to the number of electrons traversing the tube and striking the anode. As a result, the X-ray exposure and the radiation dose to the patient are directly proportional to the mA. For instance, doubling the mA will double the radiation dose. As the number of X-rays produced and radiation dose are also proportional to the duration of exposure, the product of this duration in seconds and the tube current is often represented in units of milliampere-seconds (mAs).

The tube voltage (in peak kilovoltage [kVp]) determines the energy of the electrons impinging on the anode and thereby affects the energy of the resultant X-rays. The bremsstrahlung X-rays are produced with a continuous energy spectrum, with the maximum energy depending upon the energy of the electrons and thus on the kVp. Characteristic X-rays of discrete energies below the electron energy can also be produced by X-ray fluorescence of the target material. Thus average or effective X-ray energy of the spectrum depends on kVp. As a result, the proper kVp is often selected such that it optimizes the image contrast for the task at hand. In addition, higher-energy electrons are more efficient at producing X-rays, and thereby the number of X-rays also increases with kVp. In fact, the number of X-rays produced and the radiation dose to the patient typically vary as the square of kVp.

As is traditional in radiography, a filter (typically copper or aluminum) is placed between the X-ray beam and the patient to absorb low-energy X-rays that have little potential of traversing beyond the first few centimeters within the patient and therefore would only contribute to the patient’s surface dose without contributing to the generation of the image. In CT, a “bowtie” filter is also used to minimize the exposure on the periphery of the projection while maintaining adequate exposure at the center. Both of these types of filters can affect the energy spectrum of the X-rays impinging upon the patient.

The original commercial CT scanners could only image a single slice at a time. The patient was then indexed and a subsequent slice was acquired. Although the time necessary to acquire a single slice was quite short, perhaps less than 1 second, each slice was imaged independently, and thus it may take a reasonable amount of time to image a specified volume of the patient. Two advancements in the 1980s led to a more efficient imaging of a volume of the patient. In the original scanners, the gantry would complete a single rotation during the acquisition of a single slice. The gantry would then need to reset in order to acquire the next slice. To address this limitation, the helical approach to CT scanning was developed, whereby a gantry was developed using slip-ring technology that could rotate continuously during the acquisition. In addition, the bed moved during the acquisition and thus the path of the X-ray tube formed a helix around the patient. In this manner, an entire volume of the patient could be scanned in a single acquisition without having to reset the gantry along the way. In addition, multiple CT slices could be acquired simultaneously by providing several rings of detectors in the axial or z-direction. In the past, the third-generation CT detector assembly comprised a 1D array of small radiation detectors. In the multidetector design, the array now comprised a 2D matrix, both in the azimuthal direction about the ring and also in the z-direction into the ring. The number of available rings in a multidetector CT design soon went from 4 slices to 16, 32, or 64 slices or even more. These advancements allowed for a volume of the patient to be imaged more efficiently and faster and thereby led to a subsequent increase in the clinical utilization of CT. More recently, the incorporation of a second X-ray source into the gantry design has led to even faster acquisition of the CT data.

For helical CT, the “pitch” describes the speed of the imaging table, defined by the length that the table traverses in a single rotation of the CT gantry relative to the nominal beam width. As a result, if the distance the table traversed during a gantry rotation matches the beam width, this is characterized as a pitch of 1.0 to 1 (1.0:1). If the table travels 50% faster, the pitch would be 1.5:1, indicating stretching of the helix and slight undersampling within the acquisition.

As with all medical imaging, the evaluation of image quality depends on the clinical task at hand. In some instances, spatial resolution, that is, the ability to discern small lesions or represent fine detail, is of clinical importance, whereas, in other cases, outstanding contrast resolution is essential. As a result, the three parameters of image quality of importance are spatial resolution, image contrast, and noise.

The spatial resolution is typically defined by the X-ray focal spot size and the detector dimensions in both the transverse and axial or z-direction. The smaller the detector and focal spot size, the higher the spatial resolution. In addition, a thinner slice thickness would reduce the partial volume effect in the axial or z-direction.

As discussed previously, the choice of kVp can affect image contrast; thus the kVp should be determined based on the clinical task.

Quantum noise within the CT image depends on the number of detected X-ray quanta incorporated into a CT transverse image. As described previously, the number of X-rays produced depends on both kVp and mAs. The fraction of those detected further depends on the size of the patient, the slice width, the pitch, and smoothing during image reconstruction. In other words, practically all aspects of the CT acquisition affect quantum noise in the CT image. The magnitude of the quantum noise is often parameterized by the “noise index,” which is defined by the standard deviation of the pixel values within a standard uniform CT phantom.