indicating the disease progress of a subject by fitting its ADAS scores to this curve. Similarly, Delor et al. [2] compute a disease onset time by adjusting subjects according to their CDR-SB score.
The approach presented in this work builds upon these methods. Here, quantile regression is used to estimate typical trajectories of clinical biomarkers (see Sect. 2). In detail, two models are trained, one for the transition from CN to MCI and one for the MCI-to-AD conversion. These models are then combined to a multi-stage model for the whole course of the disease. Thereafter, a probabilistic model is derived that allows the estimation of a subjects current disease progress and rate of progression based on measured biomarker values. The approach is flexible with regard to the considered biomarkers, which can be based, for example, on cognitive scores, neuroimaging, or both. Moreover, missing measurements are handled in a natural way, this means, the approach can be employed even if the set of observed biomarkers is incomplete. The proposed disease progress estimation is evaluated in Sect. 3 using clinical data. Its applicability for different classification tasks is demonstrated at the end of this section.
2 Methods
To model disease progression, the existence of a set of biomarker values 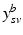 acquired from multiple subjects
acquired from multiple subjects  during multiple visits
during multiple visits  is assumed. Here,
is assumed. Here,  denotes the index of the biomarker. Each biomarker vector is associated with the time
denotes the index of the biomarker. Each biomarker vector is associated with the time 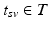 of acquisition, measured in days after the first (baseline) visit, as well as the diagnosis
of acquisition, measured in days after the first (baseline) visit, as well as the diagnosis 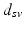 that was given during each visit. The number of visits can vary for each subject,
that was given during each visit. The number of visits can vary for each subject, 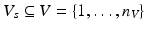 . Also, the biomarkers acquired at each visit might differ, such that
. Also, the biomarkers acquired at each visit might differ, such that 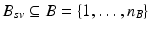 .
.
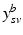 acquired from multiple subjects
acquired from multiple subjects 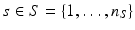 during multiple visits
during multiple visits 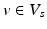 is assumed. Here,
is assumed. Here, 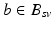 denotes the index of the biomarker. Each biomarker vector is associated with the time
denotes the index of the biomarker. Each biomarker vector is associated with the time 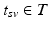 of acquisition, measured in days after the first (baseline) visit, as well as the diagnosis
of acquisition, measured in days after the first (baseline) visit, as well as the diagnosis 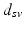 that was given during each visit. The number of visits can vary for each subject,
that was given during each visit. The number of visits can vary for each subject, 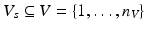 . Also, the biomarkers acquired at each visit might differ, such that
. Also, the biomarkers acquired at each visit might differ, such that 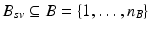 .
.In the training phase of the presented method, characteristic trajectories of biomarkers in the course of disease progression are learned based on a number of training subjects (Sect. 2.1). These models are then employed in the test phase to estimate how far and how fast test subjects have progressed along the disease trajectory (Sect. 2.2).
2.1 Model Learning
Aim of the model training phase is to learn the temporal trajectory of biomarker evolution throughout the disease by determining the probability that a certain biomarker b has a value 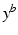 at a specified time point. More technically, each measured biomarker value
at a specified time point. More technically, each measured biomarker value 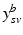 is understood as an observation of a response variable
is understood as an observation of a response variable 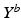 at a disease progress (DP)
at a disease progress (DP) 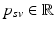 (the explanatory variable or covariate). The conditional distribution of
(the explanatory variable or covariate). The conditional distribution of 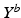 given p is then denoted by
given p is then denoted by 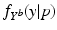 .
.
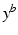 at a specified time point. More technically, each measured biomarker value
at a specified time point. More technically, each measured biomarker value 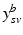 is understood as an observation of a response variable
is understood as an observation of a response variable 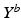 at a disease progress (DP)
at a disease progress (DP) 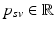 (the explanatory variable or covariate). The conditional distribution of
(the explanatory variable or covariate). The conditional distribution of 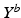 given p is then denoted by
given p is then denoted by 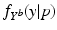 .
.A disease progression model 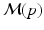 comprises the distributions of all biomarkers in B on a domain
comprises the distributions of all biomarkers in B on a domain 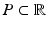 , such that
, such that 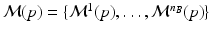 with
with 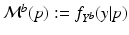 for
for 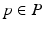 . Another way of representing the model is by its q-quantile functions
. Another way of representing the model is by its q-quantile functions 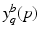 , which can be derived directly from
, which can be derived directly from 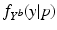 (for example, the median trajectory is denoted by
(for example, the median trajectory is denoted by 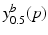 ).
).
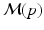 comprises the distributions of all biomarkers in B on a domain
comprises the distributions of all biomarkers in B on a domain 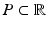 , such that
, such that 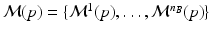 with
with 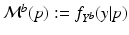 for
for 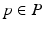 . Another way of representing the model is by its q-quantile functions
. Another way of representing the model is by its q-quantile functions 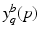 , which can be derived directly from
, which can be derived directly from 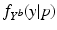 (for example, the median trajectory is denoted by
(for example, the median trajectory is denoted by 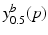 ).
).The learning of a model consists of three main steps. First, the training subjects have to be temporally aligned to establish correspondences between the time points of observation. Progression models are then estimated using quantile regression to learn the probability distributions 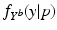 . Since temporal alignment is based on the point of conversion from either CN to MCI or MCI to AD, two separate models are learned. These two models are then combined to a multi-stage progression model.
. Since temporal alignment is based on the point of conversion from either CN to MCI or MCI to AD, two separate models are learned. These two models are then combined to a multi-stage progression model.
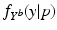 . Since temporal alignment is based on the point of conversion from either CN to MCI or MCI to AD, two separate models are learned. These two models are then combined to a multi-stage progression model.
. Since temporal alignment is based on the point of conversion from either CN to MCI or MCI to AD, two separate models are learned. These two models are then combined to a multi-stage progression model.Temporal Alignment of the Training Data. Temporal alignment aims at associating the time points  of biomarker acquisition to the corresponding DP
of biomarker acquisition to the corresponding DP  . In detail, the goal is to find a strictly monotonically increasing time warp function
. In detail, the goal is to find a strictly monotonically increasing time warp function 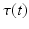 that maps the subject-specific acquisition time
that maps the subject-specific acquisition time 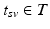 to the population-based disease progress
to the population-based disease progress 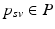 , such that
, such that 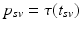 . During model training, the time point
. During model training, the time point 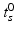 at which the clinical diagnosis changes and thus indicates transition to a more severe disease state is set to
at which the clinical diagnosis changes and thus indicates transition to a more severe disease state is set to 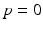 , that means
, that means
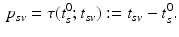
For this reason, a specific model is trained for each transition phase (here, CN-to-MCI and MCI-to-AD). To identify 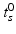 , the visits
, the visits 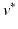 and
and 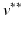 with the last CN (MCI) and the first MCI (AD) diagnosis are determined. The time point of conversion is then assumed to be the average of these two visits, i.e.
with the last CN (MCI) and the first MCI (AD) diagnosis are determined. The time point of conversion is then assumed to be the average of these two visits, i.e. 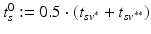 .
.
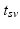 of biomarker acquisition to the corresponding DP
of biomarker acquisition to the corresponding DP 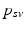 . In detail, the goal is to find a strictly monotonically increasing time warp function
. In detail, the goal is to find a strictly monotonically increasing time warp function 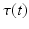 that maps the subject-specific acquisition time
that maps the subject-specific acquisition time 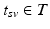 to the population-based disease progress
to the population-based disease progress 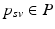 , such that
, such that 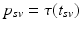 . During model training, the time point
. During model training, the time point 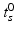 at which the clinical diagnosis changes and thus indicates transition to a more severe disease state is set to
at which the clinical diagnosis changes and thus indicates transition to a more severe disease state is set to 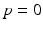 , that means
, that means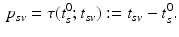
(1)
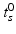 , the visits
, the visits 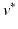 and
and 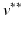 with the last CN (MCI) and the first MCI (AD) diagnosis are determined. The time point of conversion is then assumed to be the average of these two visits, i.e.
with the last CN (MCI) and the first MCI (AD) diagnosis are determined. The time point of conversion is then assumed to be the average of these two visits, i.e. 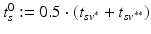 .
.Learning Disease Progression Model. The conditional distributions 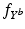 are learned independently for each biomarker using quantile regression via vector generalised additive models (VGAMs) [11]. In contrast to logistic or exponential regression [10], VGAMs do not depend on prior assumptions on the functional form for each predictor variable other than their smoothness. However, the domain P of
are learned independently for each biomarker using quantile regression via vector generalised additive models (VGAMs) [11]. In contrast to logistic or exponential regression [10], VGAMs do not depend on prior assumptions on the functional form for each predictor variable other than their smoothness. However, the domain P of 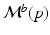 is limited to the progress interval contained in the sample set. This means P is given by
is limited to the progress interval contained in the sample set. This means P is given by ![$$P=[p_-,p_+]$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq39.gif) , with
, with 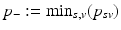 and
and 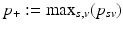 being the earliest and latest observed DP, respectively. Therefore, the models are extrapolated by a linear extension of the underlying predictor functions (see [11] for details) and
being the earliest and latest observed DP, respectively. Therefore, the models are extrapolated by a linear extension of the underlying predictor functions (see [11] for details) and 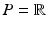 is assumed in the following.
is assumed in the following.
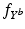 are learned independently for each biomarker using quantile regression via vector generalised additive models (VGAMs) [11]. In contrast to logistic or exponential regression [10], VGAMs do not depend on prior assumptions on the functional form for each predictor variable other than their smoothness. However, the domain P of
are learned independently for each biomarker using quantile regression via vector generalised additive models (VGAMs) [11]. In contrast to logistic or exponential regression [10], VGAMs do not depend on prior assumptions on the functional form for each predictor variable other than their smoothness. However, the domain P of 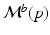 is limited to the progress interval contained in the sample set. This means P is given by
is limited to the progress interval contained in the sample set. This means P is given by ![$$P=[p_-,p_+]$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq39.gif) , with
, with 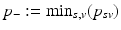 and
and 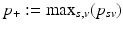 being the earliest and latest observed DP, respectively. Therefore, the models are extrapolated by a linear extension of the underlying predictor functions (see [11] for details) and
being the earliest and latest observed DP, respectively. Therefore, the models are extrapolated by a linear extension of the underlying predictor functions (see [11] for details) and 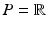 is assumed in the following.
is assumed in the following.
Fig. 1.
Approach for automatically determining the optimal model offset 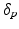 .
.
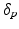 .
.
Fig. 2.
Example of the model composition. First, separate models are trained for CN-to-MCI and MCI-to-AD converters. An optimal offset between these models is then automatically determined and model training is repeated with the whole set of samples (Colour figure online).
Model Composition. To combine the CN/MCI and MCI/AD models, an optimal offset 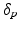 is determined by optimising the similarity of the models in the overlapping region. Given
is determined by optimising the similarity of the models in the overlapping region. Given 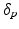 , the end point
, the end point ![$$p_+^{[1]}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq46.gif) of the CN/MCI model
of the CN/MCI model ![$$\mathcal {M}^{[1]}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq47.gif) corresponds to
corresponds to ![$$p_+^{[1]}-\delta _p$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq48.gif) in the MCI/AD model
in the MCI/AD model ![$$\mathcal {M}^{[2]}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq49.gif) . Similarly,
. Similarly, ![$$\mathcal {M}^{[2]}(p_-^{[2]})$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq50.gif) corresponds to
corresponds to ![$$\mathcal {M}^{[1]}(\delta _p+p_-^{[2]})$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq51.gif) (cf. Fig. 1). The quality of the fit is quantified by
(cf. Fig. 1). The quality of the fit is quantified by
![$$\begin{aligned} \hat{\delta }_p:=\underset{\delta _p}{{\text {argmax}}}\ \frac{1}{2}\left[ \left( \mathcal {M}^{[1]}(p_+^{[1]})-\mathcal {M}^{[2]}(p_+^{[1]}-\delta _p)\right) + \left( \mathcal {M}^{[1]}(\delta _p+p_-^{[2]})-\mathcal {M}^{[2]}(p_-^{[2]})\right) \right] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_Equ5.gif) with
with ![$$\mathcal {M}^{[1]}(p)-\mathcal {M}^{[2]}(q)=\frac{1}{|B|}\sum _{b\in B}\int f_{Y^b}^{[1]}(y|p) - f_{Y^b}^{[2]}(y|q)\ dy$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq52.gif) being the area between the corresponding density functions (averaged over all biomarkers). After determining
being the area between the corresponding density functions (averaged over all biomarkers). After determining 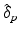 , the multi-stage model is retrained using the full set of samples with
, the multi-stage model is retrained using the full set of samples with 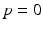 defined as the point of conversion from CN to MCI (see Fig. 2).
defined as the point of conversion from CN to MCI (see Fig. 2).
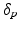 is determined by optimising the similarity of the models in the overlapping region. Given
is determined by optimising the similarity of the models in the overlapping region. Given 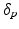 , the end point
, the end point ![$$p_+^{[1]}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq46.gif) of the CN/MCI model
of the CN/MCI model ![$$\mathcal {M}^{[1]}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq47.gif) corresponds to
corresponds to ![$$p_+^{[1]}-\delta _p$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq48.gif) in the MCI/AD model
in the MCI/AD model ![$$\mathcal {M}^{[2]}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq49.gif) . Similarly,
. Similarly, ![$$\mathcal {M}^{[2]}(p_-^{[2]})$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq50.gif) corresponds to
corresponds to ![$$\mathcal {M}^{[1]}(\delta _p+p_-^{[2]})$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq51.gif) (cf. Fig. 1). The quality of the fit is quantified by
(cf. Fig. 1). The quality of the fit is quantified by![$$\begin{aligned} \hat{\delta }_p:=\underset{\delta _p}{{\text {argmax}}}\ \frac{1}{2}\left[ \left( \mathcal {M}^{[1]}(p_+^{[1]})-\mathcal {M}^{[2]}(p_+^{[1]}-\delta _p)\right) + \left( \mathcal {M}^{[1]}(\delta _p+p_-^{[2]})-\mathcal {M}^{[2]}(p_-^{[2]})\right) \right] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_Equ5.gif)
![$$\mathcal {M}^{[1]}(p)-\mathcal {M}^{[2]}(q)=\frac{1}{|B|}\sum _{b\in B}\int f_{Y^b}^{[1]}(y|p) - f_{Y^b}^{[2]}(y|q)\ dy$$](/wp-content/uploads/2016/09/A339424_1_En_30_Chapter_IEq52.gif) being the area between the corresponding density functions (averaged over all biomarkers). After determining
being the area between the corresponding density functions (averaged over all biomarkers). After determining 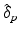 , the multi-stage model is retrained using the full set of samples with
, the multi-stage model is retrained using the full set of samples with 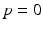 defined as the point of conversion from CN to MCI (see Fig. 2).
defined as the point of conversion from CN to MCI (see Fig. 2).2.2 Progress Estimation
Once the disease progression model is built, the aim is to estimate the progress of any given subject. However, the point of conversion 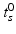 is usually unknown and thus Eq. (1) cannot be employed. Progress estimation is accomplished by finding the most likely time warp
is usually unknown and thus Eq. (1) cannot be employed. Progress estimation is accomplished by finding the most likely time warp 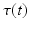 that optimally fits the evolution of the biomarkers, as measured from the patient, into the progression model
that optimally fits the evolution of the biomarkers, as measured from the patient, into the progression model 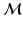 .
.
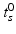 is usually unknown and thus Eq. (1) cannot be employed. Progress estimation is accomplished by finding the most likely time warp
is usually unknown and thus Eq. (1) cannot be employed. Progress estimation is accomplished by finding the most likely time warp 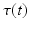 that optimally fits the evolution of the biomarkers, as measured from the patient, into the progression model
that optimally fits the evolution of the biomarkers, as measured from the patient, into the progression model 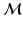 .
.Let 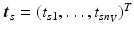 be the vector containing the time points of all visits of subject s and
be the vector containing the time points of all visits of subject s and 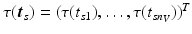 . Let further
. Let further  be the biomarker vector measured for s, with
be the biomarker vector measured for s, with 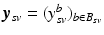 denoting the values acquired at visit v. Based on
denoting the values acquired at visit v. Based on 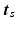 , the most probable time warp
, the most probable time warp 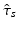 given
given 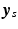 is determined by maximising the logarithm of the likelihood function
is determined by maximising the logarithm of the likelihood function 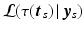 . This means
. This means
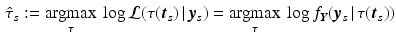
with 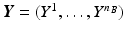 . The joint probability of all observations
. The joint probability of all observations 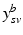 is then
is then
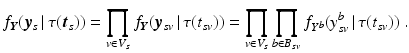 whereat all biomarker observations are assumed to be independent of each other.
whereat all biomarker observations are assumed to be independent of each other.
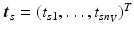 be the vector containing the time points of all visits of subject s and
be the vector containing the time points of all visits of subject s and 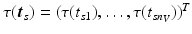 . Let further
. Let further  be the biomarker vector measured for s, with
be the biomarker vector measured for s, with 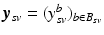 denoting the values acquired at visit v. Based on
denoting the values acquired at visit v. Based on 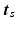 , the most probable time warp
, the most probable time warp 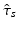 given
given 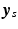 is determined by maximising the logarithm of the likelihood function
is determined by maximising the logarithm of the likelihood function 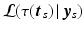 . This means
. This means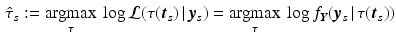
(2)
 . The joint probability of all observations
. The joint probability of all observations 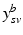 is then
is then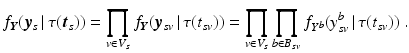
A simple translational time warp parameterisation is given by
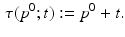
Here, the disease progress (DP) 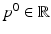 is an offset that indicates how far the subject has progressed in the course of disease at the time point of the first visit. However, this simple model cannot accommodate for different rates of progression, which are known to exist between subjects [3]. If
is an offset that indicates how far the subject has progressed in the course of disease at the time point of the first visit. However, this simple model cannot accommodate for different rates of progression, which are known to exist between subjects [3]. If 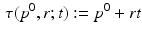
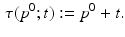
(3)
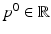 is an offset that indicates how far the subject has progressed in the course of disease at the time point of the first visit. However, this simple model cannot accommodate for different rates of progression, which are known to exist between subjects [3]. If
is an offset that indicates how far the subject has progressed in the course of disease at the time point of the first visit. However, this simple model cannot accommodate for different rates of progression, which are known to exist between subjects [3]. If 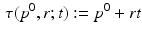
(4)
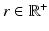 is a scaling factor indicating the disease progression rate (DPR). The optimal values
is a scaling factor indicating the disease progression rate (DPR). The optimal values 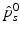 and
and 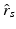 for DP and DPR are determined by maximising Eq. (2) over all
for DP and DPR are determined by maximising Eq. (2) over all 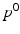 and r, i.e.
and r, i.e. 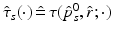 . In general, more complex time warps definitions are possible.
. In general, more complex time warps definitions are possible.




