(1)
Radiology – Neuroradiology Section, S. Paolo Hospital, Bari, Italy
1.1 Spine Stability
The spine is a multiarticular structure composed by motion segments (MS) whose correct function has as prerequisite the stability.
There exist in literature a number of definitions of stability.
The American Academy of Orthopedic Surgeons defined it as “the capacity of the vertebrae of remaining cohesive in all physiological body movements” [1].
White and Panjabi considered the clinical stability as “the ability of the spine under physiologic loads to limit patterns of displacement to not damage or irritate the spinal cord and nerve roots and to prevent incapacitating deformity or pain caused by structural changes” [2].
Spinal stability is a fundamental property for the protection of nervous elements, the active generation of forces in the body trunk and the transfer of them between the upper and lower limbs, the prevention of the early biomechanical deterioration of its own components and the reduction of energy expenditure during muscle action.
The key feature of the biomechanics and stability of the spine is the highly nonlinear load/displacement ratio, the effort required for movement significantly changing in its various phases [3].
In every MS the initial part of range of motion (ROM), on either sides of neutral posture, meets a scarce resistance and requires a relatively low effort, because of the general laxity status of ligaments and joint capsules. This part of motion, referred to as neutral zone (NZ), is replaced by the elastic zone (EZ) where the ligaments, capsules, fascias and tendons going in tension require more effort per unit of displacement nearing the ends of ROM.
In this way two opposed needs are met, reducing the muscle effort near the neutral posture and ensuring stability at the end of joint excursion.
Each vertebra can perform with respect to adjacent vertebrae, three translations and three rotations in relation to each of the x-, y-, z- Cartesian axes of space and various combinations of main and coupled movements.
Each movement has its ROM, NZ and EZ.
Stability implies an appropriate relationship between NZ and EZ even within a normal ROM.
The stabilization of the spine is guaranteed by a stabilization system consisting of three closely related subsystems (Fig. 1.1) [3] including:
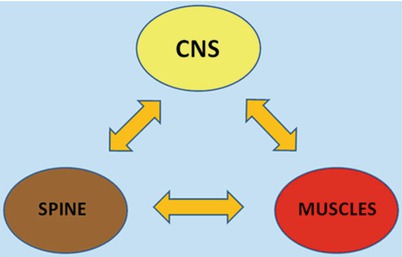

Fig. 1.1
Three strictly related subsystems control the stability of the spine: the spinal column, the muscles and the central nervous system. In case of damage to one subsystem, more compensatory work is played by the others in order to preserve stability
The spinal bones and joints or passive subsystem
The muscles forming the active subsystem
A central control unit, the CNS
1.1.1 Spinal Bones Joints and Ligaments
The passive subsystem plays a structural role, ensuring spinal stability, namely, within the elastic zone. It also has a transducer function carried out from a number of mechanoreceptors located within the joint capsules, discs and ligaments which send a continuous flow of proprioceptive inputs about the load status, spatial position and movement from each MS to CNS. On the basis of this information flow, CNS replays through an appropriate and coordinate muscle activity [4].
The vertebral body is the key element of the load-bearing system. It mainly consists of spongy trabecular bone which plays a crucial role in determining the strength and resilience of the vertebral body. Compressive loads are first accepted by vertical trabecular struts joining directly the vertebral endplates. Vertical columns, if isolated, would tend to bow and lose their load-bearing capacity if these were not restrained and maintained right by tension of horizontal trabeculae (Figs. 1.2 and 1.3). It is this conversion of vertical loads in transverse tensions that confers weight-bearing resistance to vertebral body.
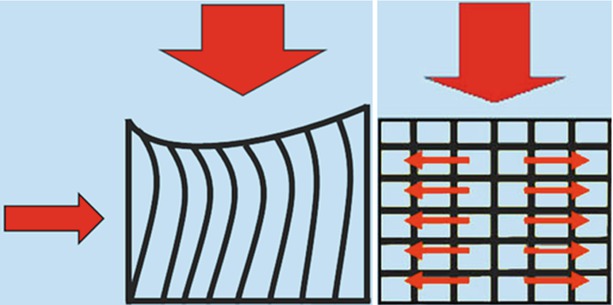

Figs. 1.2 and 1.3
The vertical compressive loads are first accepted by vertical trabecular columns which transmit forces between the endplates. The intrinsic tendency to bow of isolated vertical columns (Fig. 1.2) is restrained by horizontal lamellae whose tension favours the radial dispersion of forces conferring resilience to the vertebral body (Fig. 1.3)
A solid bony block would be heavy and, like all crystalline structures, unable to bear dynamic loads which could fracture it, whereas, conversely, a box of cortical shell would easily collapse under compressive forces because of scarce resilience of cortical bone. Cancellous bone guarantees the best load/resistance ratio.
The resistance of vertebral spongiosa either depends on trabecular architecture and bone density.
The vertebral spongiosa of any vertebra contains four main trabecular systems having a quite constant orientation: a vertical system between endplates which transmits axial loads, a curved system running in neural arc and two curved systems joining the endplates with the articular and spinous processes which anchor the neural arc to vertebral body resisting shearing forces (Fig. 1.4).
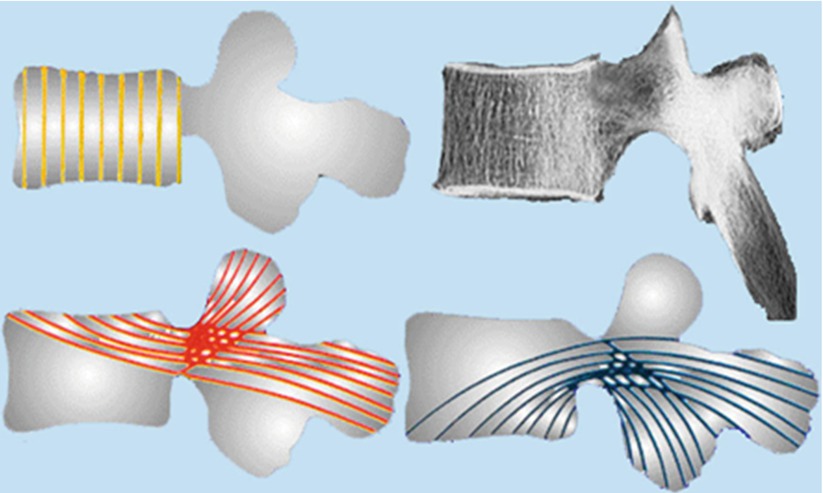

Fig. 1.4
The load-bearing capacity of the vertebral body depends on trabecular architecture. The vertebral spongiosa contains four main trabecular systems including a vertical system between endplates, a curved system running in neural arc and two curved oblique systems joining the endplates with the articular and spinous processes which anchor the neural arc to vertebral body resisting shearing forces
The bone loss in osteoporosis results in an exponential reduction of resistance. During early stages of osteoporosis, the elective reabsorption of transverse connections leads to a progressive relative elongation of vertical columns, whose resistance decreases by the square of length. Later, the thinning of columns themselves also contributes to a quadratic loss of strength with a summation of both effects.
Out of any pathological change, vertebral endplates can fail by fracturing following repeated stresses.
When a vertebral body is compressed, a part of the energy applied to deform it will be lost and, when the load is removed, less energy is available for it to restore the initial shape, which is so not immediately regained. This mechanical phenomenon, defined as hysteresis, expresses the amount of energy lost during the deformation of any solid structure. By virtue of hysteresis, a structure regains its original shape at a rate and extent different to that at which it was deformed. If forces are applied with many repetitions and sufficient frequency, the vertebral body, like any material, is unable to recover and accumulate small weaknesses, losing gradually stiffness, and, finally, fails under a stress much less than that could damage it if applied a single time [5].
Failure fractures of the vertebral endplates may occur after as few as 30–80 applications of forces corresponding to 50–80 % of ultimate compressive strength (normally between from 3,000 to 10,000 N). These forces are within the ranges occurring during normal daily activities [6].
Endplate fractures are now considered a possible cause of internal disc disruption and discogenic pain [7].
The annulus acts as the first ligament for restraining the complex 3-D movements a vertebra can perform.
The oblique alternating arrangement of collagen fibres between adjacent lamellae (with a degree of 65–70° to endplate plane) and the degree of obliquity of fibres within each lamella both optimize the capacity to restrain movements in all directions. A steeper orientation of lamellar fibres would increase the resistance to distraction, but it would compromise that to sliding and twisting; a flatter inclination would enhance control of twisting, but it would lessen that of distraction and bending.
Adjacent to vertebral endplates, the disc acts as shock absorber of the forces transmitted to the head and brain during walking and jumping.
Both nucleus and inner annulus are involved in weight-bearing. The nucleus pulposus mainly works in the NZ bearing low axial loads, while the stiffer annulus fibrosus accepts a larger proportion of the highest loads. The densely packed lamellae confer compression stiffness to annulus, but, over time, an isolated annulus under sustained loads tends to buckle and collapse.
The nucleus provides an internal bracing mechanism. Like a ball of fluid, the nucleus can be deformed but not compressed. Under axial compressive load it expands radially stretching the annulus and pushing away the opposite endplates. The vertical pressure transmits part of load from one vertebra to the next, lessening the tension created in the annulus fibrosus. The radial pressure stretches and braces the annulus preserving the vertical orientation of lamellae, avoiding their buckling and increasing their capacity to transmit loads [8] (Fig. 1.5). The cooperative action of the nucleus and the annulus enhances the disc capacity of bearing higher and prolonged loads.
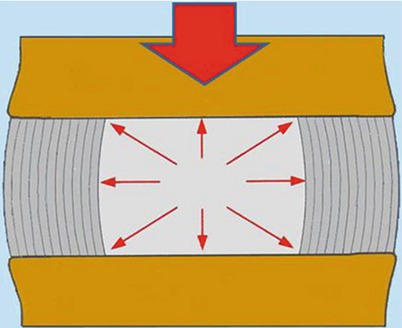

Fig. 1.5
A well-pressurized hydrated nucleus pulposus provides an internal bracing to annulus lamellae aiding annulus to contribute to weight-bearing. The cooperative action consents to disc to bear sustained and higher loads
This mechanism is lost in case of degenerative depressurization of nucleus pulposus that leads to external and internal buckling of annular lamellae. Buckling accelerates and favours the further annulus disruption (Fig. 1.6).
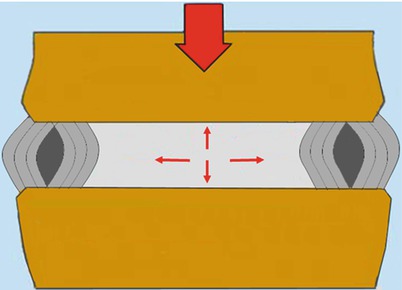

Fig. 1.6
As a consequence of disc degeneration, the nucleus pulposus loses its internal pressure favouring the collapse, buckling and tearing of annulus
In addition, under compression, a part of energy is used and stored to stretch the annulus and then released soon after the discharge of the spine. This momentary diversion of energy attenuates the speed of transmission of the force from a vertebra to another, preserving the adjacent endplates.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree