and Rakhi Kaila2
(1)
School of Physics, University of New South Wales, Sydney, NSW, Australia
(2)
School of Medicine, University of New South Wales, Sydney, NSW, Australia
Abstract
It seems nature has evolved as an interplay between a great many organic and inorganic compounds. The result is there is a considerable number of elements essential for higher life forms i.e. animals and humans. Many elements are cofactors of rather integrated parts of, enzyme and of proteins involved in electron transfer and oxygen transport. The physiological processes commonly involve an electrolyte solution containing as the major ions Na+, K+, Mg2+, Ca2+, and Cl−. Many important biopolymers like DNA, RNA and ionic mucopolysaccharides and also the aggregates of charged monomers like biological membranes, are highly charged and interact strongly with these ions. in higher organisms. Most of these are also unevenly distributed between intracellular and extra cellular spaces with the concentration gradients maintained through energy consuming active transport. Temporary changes in these ion gradients are used in nature as means of signal transmission.
10.1 Sodium–Potassium Ion Binding: Biological Systems
It seems nature has evolved as an interplay between a great many organic and inorganic compounds. The result is there is a considerable number of elements essential for higher life forms i.e. animals and humans. Many elements are cofactors of rather integrated parts of, enzyme and of proteins involved in electron transfer and oxygen transport. The physiological processes commonly involve an electrolyte solution containing as the major ions Na+, K+, Mg2+, Ca2+, and Cl−. Many important biopolymers like DNA, RNA and ionic mucopolysaccharides and also the aggregates of charged monomers like biological membranes, are highly charged and interact strongly with these ions. in higher organisms. Most of these are also unevenly distributed between intracellular and extra cellular spaces with the concentration gradients maintained through energy consuming active transport. Temporary changes in these ion gradients are used in nature as means of signal transmission. All essential elements in biological systems have at least one potentially valuable magnetic isotope. In NMR a relatively small group of magnetic nuclei, 1H, 2H, 13C, 15N and 31P have been routinely used as a source of diagnostics and imaging. In an axially symmetric complex undergoing isotopic rotation the chemical shift anisotropy (CSA) contribution to the relaxation rates R1 (=1/T1) and R2 (=1/T2) can be approximately written as [1]
![$$ \text R_{1} = \left({1/15} \right)[\gamma^{2} \text B_{0}^{2} (^{} \Updelta \sigma )^{2}][(2\tau_{c})/(1 + \omega^{2} \tau_{c}^{2})] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equa.gif) and
and
![$$ \text R_{2} = \left({1/90} \right)[\gamma^{2} \text B_{0}^{2}
(\Updelta \sigma)^{2}][(8\tau_{c}) + 6\tau_{c}/(1 + \omega^{2}
\tau_{c}^{2})] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equb.gif)
![$$ \text R_{1} = \left({1/15} \right)[\gamma^{2} \text B_{0}^{2} (^{} \Updelta \sigma )^{2}][(2\tau_{c})/(1 + \omega^{2} \tau_{c}^{2})] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equa.gif)
![$$ \text R_{2} = \left({1/90} \right)[\gamma^{2} \text B_{0}^{2}
(\Updelta \sigma)^{2}][(8\tau_{c}) + 6\tau_{c}/(1 + \omega^{2}
\tau_{c}^{2})] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equb.gif)
Here Δσ = 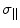 (parallel component)
(parallel component) 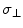 (perpendicular component) = CSA in regard to the two major axis, parallel and perpendicular to the major orientation of a macromolecule, B0 = the static magnetic field applied in the standard z-direction in the laboratory, τc = the correlation time between the interactions under analysis, ω = the resonance frequency of the macromolecule ≈ γB0, γ = the gyromagnetic ratio of the macromolecule. For the case of CSA, R1 will increase with B0, for small fields. For ωτc >1 the second set of terms within the brackets [ ] for R1, will amount to
(perpendicular component) = CSA in regard to the two major axis, parallel and perpendicular to the major orientation of a macromolecule, B0 = the static magnetic field applied in the standard z-direction in the laboratory, τc = the correlation time between the interactions under analysis, ω = the resonance frequency of the macromolecule ≈ γB0, γ = the gyromagnetic ratio of the macromolecule. For the case of CSA, R1 will increase with B0, for small fields. For ωτc >1 the second set of terms within the brackets [ ] for R1, will amount to 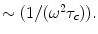 Since
Since 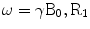 will decrease as
will decrease as 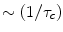 meaning less rapid pulsing. Eventually as ωτc ≫1, R1 will become independent of B0. R2 on the other hand shows somewhat different behavior. For ω τc ≫ 1 (large fields) the term within the second set of brackets [ ] becomes
meaning less rapid pulsing. Eventually as ωτc ≫1, R1 will become independent of B0. R2 on the other hand shows somewhat different behavior. For ω τc ≫ 1 (large fields) the term within the second set of brackets [ ] becomes 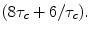 Thus R2 increases with τc.
Thus R2 increases with τc.
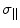 (parallel component)
(parallel component) 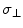 (perpendicular component) = CSA in regard to the two major axis, parallel and perpendicular to the major orientation of a macromolecule, B0 = the static magnetic field applied in the standard z-direction in the laboratory, τc = the correlation time between the interactions under analysis, ω = the resonance frequency of the macromolecule ≈ γB0, γ = the gyromagnetic ratio of the macromolecule. For the case of CSA, R1 will increase with B0, for small fields. For ωτc >1 the second set of terms within the brackets [ ] for R1, will amount to
(perpendicular component) = CSA in regard to the two major axis, parallel and perpendicular to the major orientation of a macromolecule, B0 = the static magnetic field applied in the standard z-direction in the laboratory, τc = the correlation time between the interactions under analysis, ω = the resonance frequency of the macromolecule ≈ γB0, γ = the gyromagnetic ratio of the macromolecule. For the case of CSA, R1 will increase with B0, for small fields. For ωτc >1 the second set of terms within the brackets [ ] for R1, will amount to 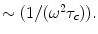 Since
Since 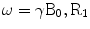 will decrease as
will decrease as 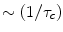 meaning less rapid pulsing. Eventually as ωτc ≫1, R1 will become independent of B0. R2 on the other hand shows somewhat different behavior. For ω τc ≫ 1 (large fields) the term within the second set of brackets [ ] becomes
meaning less rapid pulsing. Eventually as ωτc ≫1, R1 will become independent of B0. R2 on the other hand shows somewhat different behavior. For ω τc ≫ 1 (large fields) the term within the second set of brackets [ ] becomes 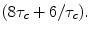 Thus R2 increases with τc.
Thus R2 increases with τc.The experimental unfavorable situation, R1/R2 < 1 is reached, whenever, ωτc >1, for the I = 1/2 nuclei. For quadrupolar nuclei (I > 1/2) evaluation of the experimental situation at hand is slightly more complicated than for I = 1 nuclei, due to several factors, notably the occurrence of non-exponential relaxation and second-order frequency shifts. Quadrupolar relaxation is caused by the interaction of a nuclear electric quadrupole moment, eQ, with fluctuating electric field gradients, eq, at the place of the nucleus. Electric field gradients are system-dependent properties and may be regarded as either intramolecular or intermolecular in origin. In isotropic systems and when ωτc ≪ 1(extremely narrowing condition) the nuclear magnetization will decay with a single exponent and we have [1],
![$$ \text R_{1} =\text R_{2}= \left( {3\pi^{2}/10} \right)[\left(\text {2I}+{3}\right)/\left(\text {2I}-{1}\right)][\left(\chi^{2}/\text {I}^{2} \right)][\left({1+\eta^{2}/3} \right)\left(\tau_{\rm c})\right]$$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equd.gif)
![$$ \text R_{1} =\text R_{2}= \left( {3\pi^{2}/10} \right)[\left(\text {2I}+{3}\right)/\left(\text {2I}-{1}\right)][\left(\chi^{2}/\text {I}^{2} \right)][\left({1+\eta^{2}/3} \right)\left(\tau_{\rm c})\right]$$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equd.gif)
Here χ = (e2qzz Q/h) is the-nuclear quadrupole coupling constant (in Hertz) and qzz (see η) is the largest component of the electric field gradient and η is the asymmetry parameter for the same gradients. η = (qxx – qyy)/qzz. As η is rarely much larger than 0.5, it will thus have a negligible influence on the relaxation rate. In biological systems the true extreme narrowing (ωτc ≪ 1) situation is usually encountered only in the case of free’ hydrated ions in solution or in the case of low-molecular weight complexes. More common is the situation when ωτc >1. In this case the decay of the longitudinal (M1) and transverse (M2) magnetizations for quadrupolar nuclei with spins I > 1 is no longer exponential but may be written for half integer spins as a weighted sum of (I + 1/2) exponentials as [1]
![$$ \text M_{1} \left(\text t \right) = \text M_{1} (\infty)1-\text k \sum\nolimits ^{{\text I + \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} }} \text i_{= 1} \left[{\text {C}_{\rm 1i} \exp \left({- \text{R}_{\rm 1i} \text t} \right)} \right] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Eque.gif)
![$$ \text{M}_{2} \left(\text t \right) = \text{M}_{2}
(0) \sum\nolimits ^{{\text I + \raise.5ex\hbox{$\scriptstyle
1$}\kern-.1em/\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} }}\text
{i}_{= 1} \left[{\text C_{\rm 2i} \exp \left({- \text{R}_{\rm 2i}
\text t} \right)} \right] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equf.gif) where
where
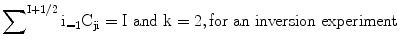 t is known in the second-order dynamic frequency shifts the resonance frequencies of the various components will not in general be the same. Furthermore although the above equation is valid for the total magnetization, the decays of the individual components, will normally not be exponential and will also depend on the length of the monitoring pulse. In studies of metal ion nuclei in biological systems we frequently encounter situations when ωτc ≈ 1.
t is known in the second-order dynamic frequency shifts the resonance frequencies of the various components will not in general be the same. Furthermore although the above equation is valid for the total magnetization, the decays of the individual components, will normally not be exponential and will also depend on the length of the monitoring pulse. In studies of metal ion nuclei in biological systems we frequently encounter situations when ωτc ≈ 1.
![$$ \text M_{1} \left(\text t \right) = \text M_{1} (\infty)1-\text k \sum\nolimits ^{{\text I + \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} }} \text i_{= 1} \left[{\text {C}_{\rm 1i} \exp \left({- \text{R}_{\rm 1i} \text t} \right)} \right] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Eque.gif)
![$$ \text{M}_{2} \left(\text t \right) = \text{M}_{2}
(0) \sum\nolimits ^{{\text I + \raise.5ex\hbox{$\scriptstyle
1$}\kern-.1em/\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} }}\text
{i}_{= 1} \left[{\text C_{\rm 2i} \exp \left({- \text{R}_{\rm 2i}
\text t} \right)} \right] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equf.gif)
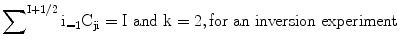
It is known that for I = 3/2 nuclei, decays of the magnetization M1 and M2 will be very nearly exponential up to ωτc ≈ 1.5 and useful expressions for the apparent relaxation rates <R1> and <R2> can be derived to for the I = 3/2, I = 5/2, I = 7/2, etc. nuclei. To a first order the longitudinal and transverse relaxation rates are given by [1]
![$$ <\text {R}_{1}> = \left({3\pi^{2}/10} \right)(\chi^{2})[(\text {2I + 3})/\{\Upgamma^{2} \left({\text {2I – 1}} \right)\}][\text {0.2J}_{1} + \text {0.8J}_{2}] $$” src=”/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equh.gif”></DIV></DIV></DIV><br />
<DIV id=Equi class=Equation><br />
<DIV class=EquationContent><br />
<DIV class=MediaObject><IMG alt=]() = \left({3\pi^{2}/10} \right)(\chi^{2})[(\text{2I} + 3)/\{\Upgamma^{2} \left({\text {2I} – 1} \right)\}][\text {0.3J}_{0} + \text {0.5J}_{2} + \text {0.2J}_{2}], $$” src=”/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equi.gif”>where JK are spectral densities that may be taken as
= \left({3\pi^{2}/10} \right)(\chi^{2})[(\text{2I} + 3)/\{\Upgamma^{2} \left({\text {2I} – 1} \right)\}][\text {0.3J}_{0} + \text {0.5J}_{2} + \text {0.2J}_{2}], $$” src=”/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equi.gif”>where JK are spectral densities that may be taken as
![$$ \text {J}_{\rm K} = [(\tau_{\rm c})/[\text {I}+ (\text {K}\omega_{0} \tau_{\rm c})^{2}]] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equk.gif)
![$$ \text {J}_{\rm K} = [(\tau_{\rm c})/[\text {I}+ (\text {K}\omega_{0} \tau_{\rm c})^{2}]] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equk.gif)
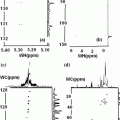
These equations may be used in a slightly modified form to cover also the experimental situation when a quadrupolar nucleus is exchanging rapidly between two or more sites. Figure 10.1 (Fig. 1 [1]) is a simple depiction of the various physical quantities involved. The above two equations may be used in a slightly modified form to cover also the experimental situation when a quadrupolar nucleus is exchanging rapidly between two or more sites. For a case when the nucleus is rapidly exchanging between a bound state (B) and a ‘free’ state (F) we may write the effective spectral density as a weighted average as follows [1].
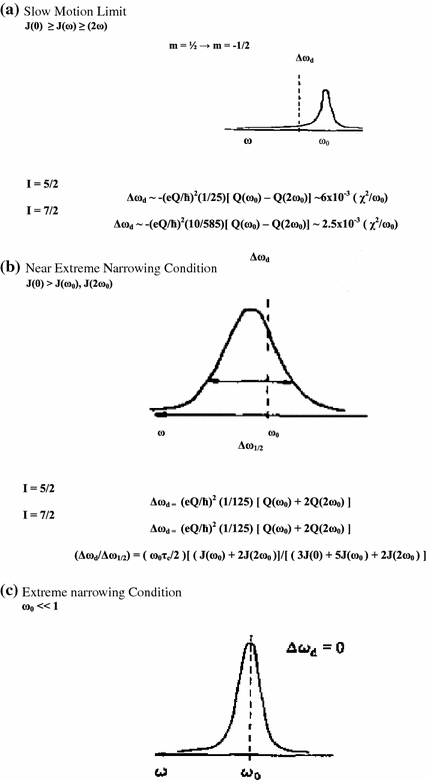
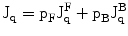

Fig. 10.1
Some general characteristics of dynamic frequency shifts
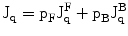
Here pF and pB are the relative populations of the two states, free and bound. JqF may be taken simply as J0F and for isotropic motion JqB can be written as [1]
![$$ \text J^{\rm B}_{\rm q} = [\left({0.1} \right)\left({\text q_{\rm zz}} \right)^{2} (\tau_{\rm cB})/[1 + (\text q\omega \tau_{\rm cB})^{2}] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equm.gif)
![$$ \text J^{\rm B}_{\rm q} = [\left({0.1} \right)\left({\text q_{\rm zz}} \right)^{2} (\tau_{\rm cB})/[1 + (\text q\omega \tau_{\rm cB})^{2}] $$](/wp-content/uploads/2016/08/A300799_1_En_10_Chapter_Equm.gif)
By using the above equations, one can derive expressions for the reduced’ relaxation rates defined as [1]
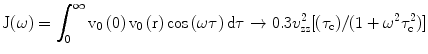 and for the special cases
and for the special cases
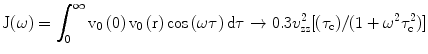
In addition to non-exponential relaxation for quadrupolar nuclei under conditions of non-extreme narrowing the NMR signal will also be modified by dynamic frequency shift changes that have been termed as ‘second-order dynamic frequency shifts (SODFS)’. These shifts were long neglected because they were always smaller than the signal line width. It took some time to be appreciated that though the dynamic shifts were always smaller than the width of the broadest component of a resonance they may well be larger than the most narrow component and thus be clearly observable in the spectrum. The effects of second-order frequency shifts for the I = 3/2 case is well known now. Under non-extreme (ω τ < 1) narrowing conditions the two transverse relaxation components will differ in resonance frequencies as well as in relaxation rates. The NMR signal will thus appear asymmetric. A further complication is that the longitudinal relaxation of the two components will in general be non-exponential and the apparent rates dependent on the length of the monitoring (normally 90°) pulse. The magnitude of the second order effects are dependent on the ratio (χ2/ωo) and will thus be particularly important in situations of large quadrupole coupling constants and low observing frequency.
The expressions for the NMR band shape for I = 5/2 and / = 7/2 nuclei—both in the presence and absence of chemical exchange are schematically summarized in the Fig. 10.1 [1]. In the limit ωτc ≫ 1, the m =/2 to m = −/2 component will dominate the spectrum because it is much narrower than the other components. The intensity of this component relative to the total intensity will be 40 % for I = 3/2, 26 % for I = 5/2 and 19 % for I = 7/2. The narrow signal will be shifted towards lower frequency with a value proportional to (χ2/ω0). Between the two limits the resonance will be more or less asymmetric with an apparent shift either to high or low frequencies depending on the values of ω0, τc and χ. The ratio of the dynamic shift to line width will in this region depend only on ω0 and τc. One should note that the temperature dependence of the apparent line width in a chemically exchanging system may deviate considerably from that observed in spin I = 1/2 systems. Considerable care must therefore be exercised when exchange rates are deduced from variable temperature studies of quadrupolar nuclei.
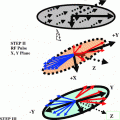
10.2 Spin 3/2 Dynamics Density Matrix Approach NMR Experiments
The NMR behavior of the spin 3/2 systems is particularly interesting in the context of biological systems because of the dependence of their NMR signal on the electrical and structural properties of the biological microenvironment. This dependence has been exploited in the context of multiple quantum-filtered (MQF) sodium NMR experiments for the study of ion fluxes during ischemia experiments and for the identification of neoplastic changes in human tissue. Imaging extensions of the NMR techniques although highly desirable are not as common in the literature because of the low concentration of sodium ions in human tissue and the inherent challenges involved in the fast spatial encoding of the sodium NMR signal. Fortunately the development of efficient spatial encoding techniques in MRI has allowed the generation of sodium images in times that are adequate for practical use in humans (data acquisition time less than 10 min). Extensions of these techniques have also been used to provide the first demonstration of in vivo MQF sodium MRI techniques in humans. The routine application of MQF techniques for the non-invasive diagnosis and monitoring of pathology in humans, however requires a more thorough understanding of the dependence of this novel image contrast on hard-to-control spatial variations in experimental parameters such as the B1 field and the B0 field. Such understanding can only be attained through a proper description of the behavior of the spin system for arbitrary values of the aforementioned experimental parameters. The standard theoretical approach for describing the spin dynamics in the presence of non-negligible relaxation behavior is based on the Redfeld equations. Analytic solutions for the Redfield equations can be obtained by reducing the Redfield equations to a system of linear differential equations in a suitably chosen basis of quantum mechanical operators. These approaches however do not reveal inherent factorizations of the solution. Such factorizations are attractive for practical use because of the natural separation they provide for the effects of the experimental parameters on the signal.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree