Categorization Models for Color Image Segmentation

(1)

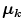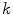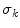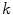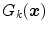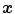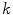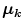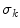In the Eq. (1) $\varvec{\mu _k}$ indicates the localization of the center or focal point for each category; $\sigma _k$ controls the volume of color space that is included in each category and the function value $G_k(\varvec{x})$ determines the membership of the color stimuli $\varvec{x}$ to a category. The $\varvec{\mu _k}$ and $\sigma _k$ values are computed through a minimization of a functional described in [14] for each category, using the color points of the boundaries and the foci of the regions obtained in [4]. Once the parameters are known, one can assign a color category for any arbitrary color stimuli 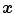$\varvec{x}$ as follows:

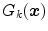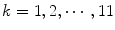Compute the model function ${G_k(\varvec{x})}$ for $k =1, 2,\cdots , 11$ .

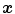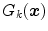Assign to the color stimuli $\varvec{x}$ the color category or index that maximizes ${G_k(\varvec{x})}$ .

The Lammens color categorization model is constructed not only in NPP color space, but also in the 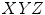and 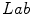spaces. This proposal does not consider intensity and saturation modifiers and despite of its novelty, it has not been extensively applied yet.

Another interesting approach about color naming and description of color composition of the scene is given by [17]. The computational model for color naming done by research in [17] adopted the ISCC-NBS dictionary [13] because this dictionary allows to carry out controlled perceptual experiments and includes basic color terms defined by Berlin and Kay [4]. In the color naming experiment 10 subjects participated and four experiments were done:

Color Listing Experiment: it is aimed at testing 11 basic color categories from Berlin and Kay’s investigation. Each subject was asked to name at least twelve colors in order to test the relevance of color terms not included in basic ones.

Color composition experiment: the aim of this experiment is to determine the vocabulary used in describing complex color scenes. The participants observed 40 photographic images in a sequence and they described the color composition of each image under the restriction to use common color terms, common modifiers of brightness and saturation and to avoid rare color names (for example, names derived from objects or materials).

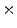Two Color-Naming Experiments: Each subject observed 267 centroid colors from the ISCC-NBS color dictionary and assigned a color name. In the first experiment 64 $\times$ 64 pixel color patches were arranged into a 9 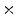$\times$ 6 matrix and were displayed to the subjects. The light gray was the display background. In the second experiment only one 200 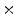$\times$ 200 pixel color patch was observed.

From these experiments, in [17] arrived at the following conclusions:

None of the subjects listed more than 14 color names during Color Listing Experiment. The eleven basic colors specified by Berlin and Kay were found in the color list. Beige, violet and cyan were also included by some of the subjects with less frequency. Modifiers for hue, saturation and luminance were not used for this color listing experiment. This stage in color naming was described as fundamental level: the color names are expressed using only generic hue or generic achromatic terms.
The subjects used almost similar vocabulary to describe image color composition in the Color Composition Experiment. Modifiers for hue, saturation and luminance were used to distinguish different types of the same hue. Although the images had rich color histograms, no more than 10 names were included in the color list. In this case, color naming can be classified in the coarse level, in which the color names are expressed using luminance and generic hue or luminance and generic achromatic term. Another level presented in the Color Composition Experiment was the medium level: color names are described adding the saturation modifiers to the coarse description.
The results obtained in the two color naming experiments were almost identical. The difference is explained by the use of different luminance modifiers. The same color is described by a different luminance modifier when it is displayed in a small and in a large window, i.e., the size of the color patches influences in the color naming decision by a subject. For this experiment the author classified the color vocabulary as minute level, in which the complete color information is given.
In general, well-defined color regions are easier to describe than dark regions, which, in general, exist due to shadows or due to illumination problems.
All experimentation confirmed that not all color terms included in the ISCC-NBS dictionary are well understood by the general public. For that reason Mojsilovic decided to use all prototype colors specified in ISCC-NBS dictionary [17], except those that were not perceived by the participants of the experiments. On the other hand, in order to reflect the participant decisions, some of the color names were changed. With all these considerations, a new color vocabulary was created in [17] for describing the color naming process.

A very interesting issue of the research is that they designed a metric in order to know the similarity of any arbitrary color point 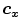$\varvec{c_{x}}$ with respect to a color prototype 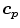$\varvec{c_{p}}$ . The new metric, which is based on the findings from the experiment, is given by the following equation:

$\begin{aligned} D(\varvec{c_p},\varvec{c_x})=D_{Lab}(\varvec{c_p},\varvec{c_x})[1+k(D_{Lab}(\varvec{c_p},\varvec{c_x}))\triangle d(\varvec{c_p},\varvec{c_x})], \end{aligned}$

(2)

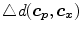where $\triangle d(\varvec{c_p},\varvec{c_x})$ is a distance function in the 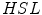color space proposed in [17] and 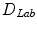$D_{Lab}$ is a distance in the 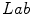color space

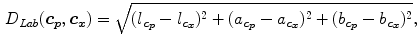
$\begin{aligned} D_{Lab}(\varvec{c_p},\varvec{c_x})=\sqrt{(l_{\varvec{c_{p}}}-l_{\varvec{c_{x}}})^2+(a_{\varvec{c_{p}}}-a_{\varvec{c_{x}}})^2+(b_{\varvec{c_{p}}}-b_{\varvec{c_{x}}})^2}, \end{aligned}$

(3)

where 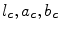$l_{\varvec{c}}, a_{\varvec{c}}, b_{\varvec{c}}$ represent the components 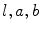of the color 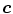$\varvec{c}$ in the 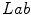color space.

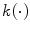In Eq. (2), $k(\cdot )$ is a function which is introduced with the aim to avoid modifying distances between very close points in

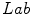space and to control the amount of increase for large distance 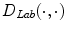$D_{Lab}(\cdot ,\cdot )$ , the factor 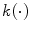$k(\cdot )$ is defined as:

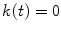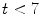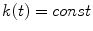, if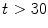

[17]. Observe that the Eq. (2) is a combination of distances of two spaces:

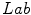and

The author remarks that any other distance function that satisfies the requirements for the color-naming metric can be used, for example, CMC or dE2000 color difference metric, that explains the non-uniformity of the

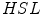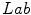space. For validation purposes, the metric was compared with human observations arriving at 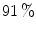$91\,\%$ agreement.

In [17] Mojsilovic proposed the application of the model to describe the color composition of the image after the color segmentation process through the Mean Shift algorithm [10].

The experimentation confirms that the human visual system performs an spatial average, which depends on color frequencies, interactions between colors, observed object size and global context. For instance: we perceived one color for uniform color regions; pixels labeled as color edge and texture edge are not averaged; edge density determines the amount of averaging performed in the textured areas: fine texture (more edge density) has more color averaging than coarse ones (less edge density). Therefore, the human color perception can be interpreted as an adaptive low-pass filter, which must be considered for any application related to human color perception [17].

Robert Benavente et al. [2] proposed a computational model based on the idea proposed by Kay and McDaniel [12]. They pointed out that color naming is a fuzzy decision. Taking into consideration this postulate, the best way to model the color naming is through the fuzzy set theory. Therefore, each color category is defined as a fuzzy set. The color naming experiment in [2] was carried out as follows:

10 subjects observed 422 color samples and they were asked to distribute 10 points among the 11 basic color categories taking in consideration the grade of belonging of the observed color sample to each of the basic color terms. When the subject was absolutely sure about the sample color name, 10 points were assigned to the corresponding category. The restriction for using only 11 color terms is justified by research in [5, 21].
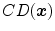For each sample, the scores were averaged and normalized to the interval. The experiment was performed twice for each subject. As a result of the color naming process, an experimental color descriptor, $CD(\varvec{x})$ , is obtained for each sample:

$\begin{aligned} CD(\varvec{x}) = [m_{{1}}(\varvec{x}), m_{{2}}(\varvec{x}),\cdots , m_{{11}}(\varvec{x}) ], \end{aligned}$

(4)

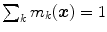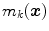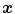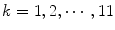where $m_{{k}}(\varvec{x}) \in [0,1]$ and $\sum \nolimits _{k} m_{{k}}(\varvec{x}) = 1$ . $m_{{k}}(\varvec{x})$ can be interpreted as the degree of membership of $\varvec{x}$ to the color category $k = 1, 2,\cdots , 11$ .

The results of the color naming experiment define the training set to find membership functions 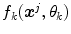$f_{k}(\varvec{x}^j,\theta _k)$ of the color fuzzy sets. In order to know the parameters, 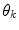$\theta _{k}$ , of each membership function (model for each color category), the minimization of the following functional

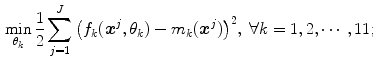
$\begin{aligned} \min _{\theta _{k}} \frac{1}{2}\sum _{j=1}^J {\left( f_{k}(\varvec{x}^j,\theta _k)-m_{{k}}(\varvec{x}^j)\right) ^2}, \; \forall k = 1,2,\cdots , 11; \end{aligned}$

(5)

is carried out, see [2]. The previous functional, Eq. (5), represents the mean squared error between the membership values of the model 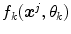$f_{k}(\varvec{x}^j,\theta _k)$ and the 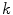-th component 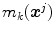$m_{k}(\varvec{x}^j)$ of the color descriptor obtained in the color naming experiment, Eq. (4); 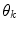$\theta _k$ is the set of parameters of the model, 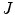is the number of samples in the training set and 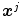$\varvec{x}^j$ is the 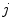-th color sample of the training set. According to [2] the model 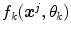$f_{k}(\varvec{x}^j,\theta _k)$ depends on the type of the color category (chromatic or achromatic).

In [2], the authors created a color space named

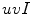, whose first two components represent the color components and the third one the intensity. They carried out the experimental work in the

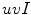space and for comparison purposes they also employed the

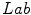space. From the color naming data and data fitting process through an optimization algorithm they concluded that the Gaussian function is a good model, as a membership function, for achromatic categories. However, they found that the combination of sigmoid and Gaussian functions is an appropriate model for chromatic categories. They also concluded that the results obtained in the

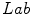space were no better than those obtained in

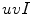space.

Seaborn et al. [19] also proposed a computational model based on fuzzy sets and considered the eleven color basic terms. The research was done in the Munsell space and the data were taken from Sturges et al. [21] investigation. As in [2] they made a distinction between membership function for achromatic and membership function for chromatic classes.

They proposed a similarity measurement based on Tversky research [22]. This measurement is compared with Euclidean distance and they conclude that the new proposal achieved a higher agreement with human judge. They compared the new similarity measurement in the

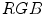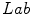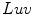and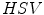

color spaces and concluded that the

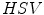space had the best performance to detect similarity and difference between colors.

Joost van de Weijer and et al. [24] elaborated a model to learn color names from real world images, through a Probabilistic Latent Semantic Analysis (PLSA), a generative model introduced by Hofmann [11] for document analysis. In the research, only the eleven color basic categories defined by Berlin and Kay are considered. The data color samples are extracted from http://lear.inrialpes.fr/data (data here were collected by the authors), from the auction website Ebay, from Google and from those published by Benavente et al. [3]. The latter data were taken in order to compare the color assignment in real world images with a chip-based approach described in [2]. Three color spaces were used:

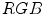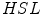and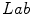

. Two ways to assign color names to individual pixel are considered [24]:

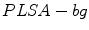model: It is based only on the pixel value. The model is expressed as follows:

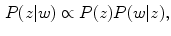
$\begin{aligned} P (z |w) \propto P (z) P (w |z), \end{aligned}$

(6)

where 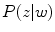$$P (z |w)$$ represents the probability of a color name 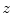$$z$$ (color category) given a pixel 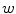$$w$$ . The prior probability over the color names is taken to be uniform [24].

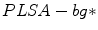model: It takes into account the pixel $$w$$

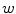and some region $$d$$

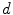, around it. The Equation for the model is the following:

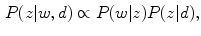
$\begin{aligned} P (z |w, d) \propto P (w |z) P (z |d), \end{aligned}$

(7)

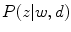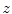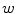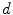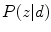where $$P (z |w,d)$$ represents the probability of a color name $$z$$ (color category) given a pixel $$w$$ in a region $$d$$ . The $$P (z |d)$$ is estimated using an EM algorithm [11].

The experimental work considers data in three color spaces: 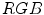, 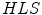and 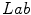. According to the investigation, the 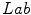space slightly outperformed the others. Besides the PLSA method, the authors employed the Support Vector Machine algorithm [6].

Menegaz et al. [16] presented a computational model obtained by a linear interpolation of a three dimensional Delaunay triangulation of the

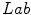color space.

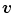Alarcon and Marroquin’s color categorization model [1], assigns to each voxel $\varvec{v}$ , with components

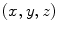, in a given color space, 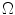$\Omega$ , a discrete probability distribution $\varvec{l}(\varvec{v}) = [l_{1}(\varvec{v}), \cdots , l_{K}(\varvec{v})]^T$ where the component 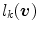$l_{k}(\varvec{v})$ is interpreted as the probability of 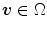$\varvec{v} \in \Omega$ to belong to the color category

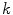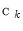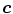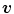, $\fancyscript{C}_{k}$ , given the color $\varvec{c}$ at $\varvec{v}$ , denoted here as 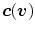$\varvec{c}(\varvec{v})$ . Note that, the components of 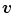$\varvec{v}$ correspond to the color 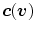$\varvec{c}(\varvec{v})$ , i.e., 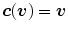$\varvec{c}(\varvec{v}) = \varvec{v}$ . Then, 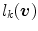$l_{k}(\varvec{v})$ is defined as follows:

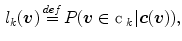
$\begin{aligned} l_{k}(\varvec{v}) \mathop {=}\limits ^{def} P(\varvec{v} \in \fancyscript{C}_{k} | \varvec{c}(\varvec{v})), \end{aligned}$

(8)

and represents the posterior probability of a voxel to belong to a color category. In [1] each category 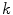is modeled as a linear combination of 3D quadratic splines

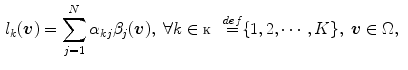
$\begin{aligned} l_k(\varvec{v}) = \sum _{j = 1}^N{\alpha _{kj}\beta _j(\varvec{v})}, \; \forall k \in \fancyscript{K} \mathop {=}\limits ^{def} \{1,2,\cdots , K\}, \; \varvec{v} \in \Omega , \end{aligned}$

(9)

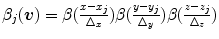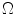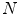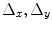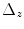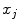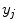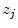where $\beta _{j}(\varvec{v}) = \beta (\frac{x - x_{j}}{\Delta _{x}}) \beta (\frac{y - y_{j}}{\Delta _{y}}) \beta (\frac{z - z_{j}}{\Delta _{z}})$ are located in a node lattice in $\Omega$ , is the number of nodes in the lattice; $\Delta _{x}, \Delta _{y}$ and $\Delta _{z}$ define the resolution of the node lattice; $x_{j}$ , $y_{j}$ , and $z_{j}$ denote the coordinates of the 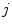-th node, 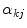$\alpha _{{kj}}$ is the contribution of each spline function 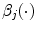$\beta _{j}(\cdot )$ to each category 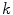and $\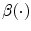beta (\cdot )$ is the quadratic basis function defined in the following equation:

$\begin{aligned} \beta (x) =\left\{ \begin{array}{ll} \frac{1}{2}(-2x^{2}+1.5), &{} |x| \in \Big [ 0,\frac{1}{2}\Big ]; \;\\ \\ \frac{1}{2}(x^{2}-3|x|+2.25), &{} |x| \in \Big [\frac{1}{2},1.5 \Big ]; \\ \\ 0, &{} |x|\ge 1.5. \end{array} \right. \end{aligned}$

(10)

In order to determine 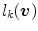$l_{k}(\varvec{v})$ in (9) one needs to compute the parameters 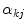$\alpha _{kj}$ . Hence, the authors propose to minimize the following functional:

$\begin{aligned} \min _{\varvec{\alpha }_k} \sum _{\varvec{v} \in \fancyscript{D} } \Big [ l_k(\varvec{v})-\sum _{j=1}^N{\alpha _{kj}\beta _j(\varvec{v})}\Big ]^{2}+\tau \sum _{\langle m,n \rangle } {(\alpha _{km}-\alpha _{kn})^2}, \; \forall k \in \fancyscript{K}, \end{aligned}$

(11)

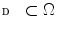where $\varvec{\alpha }_{k} = [ \alpha _{ki} ]_{i = 1,\cdots ,N}^T$ , $\fancyscript{D} \subset \Omega$ represents a voxel set for which 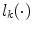$l_k(\cdot )$ is known and 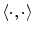$\langle \cdot , \cdot \rangle$ denotes a pair of neighboring splines. In this case, 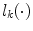$l_k(\cdot )$ is obtained, for all voxels in 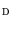$\fancyscript{D}$ , through a color naming experiment based on isolated color patches. The second term in (11) controls the smoothness between spline coefficients, 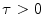$\tau > 0$ is a parameter that controls the smoothness level.

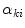The solution of the optimization problem (11) is computed by calculating the partial derivatives with respect to $\alpha _{ki}$ and setting the derivatives equal to zero, i.e.,

$\begin{aligned} -\sum _{ \varvec{v} \in \fancyscript{D} } \Big [ l_k(\varvec{v})-\sum _{j=1}^N \alpha _{kj}\beta _j(\varvec{v})\Big ] \beta _i(\varvec{v})+\tau \sum _{m \in \fancyscript{N}_i}(\alpha _{ki}-\alpha _{km}) = 0, \end{aligned}$