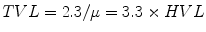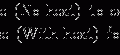, Foster D. Lasley2, Indra J. Das2, Marc S. Mendonca2 and Joseph R. Dynlacht2
(1)
Department of Radiation Oncology, CHRISTUS St. Patrick Regional Cancer Center, Lake Charles, LA, USA
(2)
Department of Radiation Oncology, Indiana University School of Medicine, Indianapolis, IN, USA
Definitions
Energy (E) measures the amount of energy in each photon.
Intensity (I) and Fluence (ϕ) measure the total number of photons per unit area, #/cm 2 .
Attenuation measures the decrease in intensity (number of photons) as a beam passes through matter.
Attenuation is a concept specific to photons. Charged particles do not undergo attenuation, but rather undergo slowing and stopping.
Intensity Versus Penetration
It is easy to get confused between these two concepts. They are very different!
Intensity (fluence, number of particles) tells you how much dose a beam can give, but not how deep that will go.
Penetration (energy, beam quality) tells you how deep the beam will go, but not how big that dose will be.
When dealing with filtration and beam hardening, intensity and penetration are actually inversely related.
Filtration decreases intensity but increases penetration by selectively filtering out lower energy photons in a poly-energetic beam.
Attenuation Coefficients
Linear attenuation coefficient (μ) measures the rate at which photons are attenuated per centimeter of material encountered (see Chapt. 6 for details).
Mass attenuation coefficient (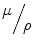
) is the linear attenuation coefficient divided by the density of the attenuating material. This is used for calculations such as “how much mass is needed for shielding?”
Partial attenuation coefficients (μ 1, μ 2, μ 3, …) are used to analyze different components of attenuation.
For example, “attenuation due to photoelectric effect”, “attenuation due to Compton scatter”, and “attenuation due to pair production”.
The sum of all partial coefficients should equal the total (linear) attenuation coefficient.
Mathematics of Attenuation (Fig. 7.1)
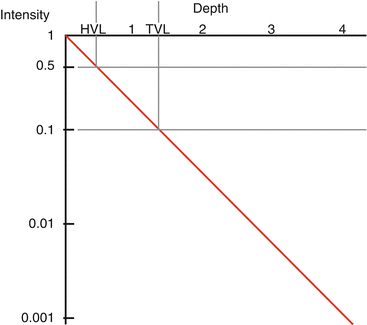
Fig. 7.1
Simple attenuation. Intensity decreases by a factor of 2 with every half value layer, and by a factor of 10 with every tenth value layer.
A narrow beam of mono-energetic photons attenuates in a simple exponential fashion:
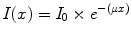
(7.1)
Starting at an initial intensity of I 0 , I decreases exponentially with Depth (x).
This equation should look familiar; it is similar to Activity (A) versus Decay Constant (λ) and Time (t) (see Chapt. 2).
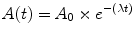
(7.2)
Attenuation coefficient relates to half–value layer (HVL) like decay constant relates to half–life:
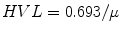
(7.3)
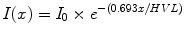
(7.4)
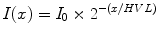
(7.5)
A tenth–value layer can be defined as 3.3 half–value layers, or 2.3/μ. This is the depth at which the primary beam has one-tenth its original intensity. This is often used for shielding calculations for a radiation facility.
