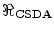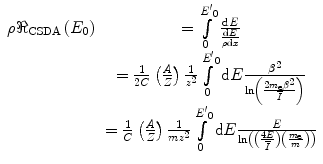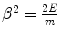(1)
Amersham, Buckinghamshire, UK
13.2 Geometry
13.3.1 Definition
13.3.3 Scaling of 
13.4 Projected Range
13.4.1 Definition
13.4.2 Detour Factor
13.5 Bragg Peak
13.6.1 Introduction
13.6.2 Electron CSDA Range
13.6.5 Positron Range
Abstract
This chapter considers one of the main manifestations of charged particle energy loss that of the penetration into matter. It begins with the derivation of the continuous slowing down approximation (CSDA) range for heavy charged particles and presents the Bragg peak. As electrons remain currently the most commonly used charged particles in radiation oncology, we review the depth–dose curves of electrons in soft tissue. Unlike energetic heavy charged particles, multiple Coulomb scatter is a significant effect upon the radiation transport of electrons and cannot be excluded in the determination of the range, as has already been examined in the context of the Fermi–Eyges theory of Sect. 6.3.7. We conclude the chapter with an examination of the ranges of positrons in matter and the probabilities of in-flight annihilation.
13.1 Introductory Comments
It follows immediately that as an energetic charged particle transfers its kinetic energy to the medium that it is traversing through, it will lose all of this energy and eventually come to rest (or, more properly, come to thermal energies). The distance between from where the particle entered the medium (either at an interface as in the case of an external beam of particles or within the medium itself as in the case of a radioactive source of charged particles) to where it has stopped is referred to as the range of the charged particle. More formally, as to be shown in Part IV of this book, as the energy loss process is a stochastic one, the range is the expectation value of the path length that the particle follows until it has stopped. In this chapter, we introduce the basic concepts and definitions of range in the context of charged particles.
Much of this chapter should be considered in parallel with the discussion of multiple Coulomb scatter presented in Chap. 6.
13.2 Geometry
Figure 13.1 shows the geometry specific to a charged particle which is incident to a medium at an angle χ to the norm. The particle penetrates the medium and is assumed to follow a tortuous path length due to multiple Coulomb scatter until it comes to rest at the points with the co-ordinates of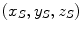 
.
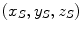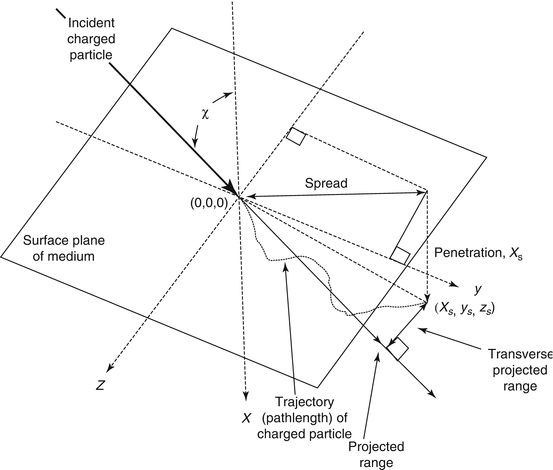
.Fig. 13.1
A charged particle is incident to the surface of a medium at an angle of χ to the normal. It follows a non-linear trajectory until it is stopped at (x s , y s , z s ). Shown are the definitions of the projected range, spread, penetration and the transverse projected range
We now consider the description of this geometry in some detail. As the particle penetrates the medium, it becomes both subject to elastic multiple Coulomb scatter from the atomic nuclei and the transfers of kinetic energy to the medium via collisions with the atomic electrons. The former leads to deviations of the particle’s trajectory from its original. The latter leads the deceleration of the particle until it reaches its terminus at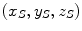 
. The path length of the projectile is the total distance travelled by the particle, and the projected range (R P) is the distance along the direction of the original trajectory to the point projected along the perpendicular from 
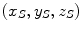. The length of this perpendicular is known as the transverse projected range. The penetration or projected range is the depth within the medium at which the particle stops (i.e. x S ). Finally, the spread is defined as the distance along the surface (i.e. the yz-plane) from the entrance point to the projection of the stopping point 
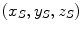at the surface, 
.
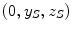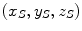. The path length of the projectile is the total distance travelled by the particle, and the projected range (R P) is the distance along the direction of the original trajectory to the point projected along the perpendicular from 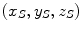. The length of this perpendicular is known as the transverse projected range. The penetration or projected range is the depth within the medium at which the particle stops (i.e. x S ). Finally, the spread is defined as the distance along the surface (i.e. the yz-plane) from the entrance point to the projection of the stopping point 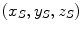at the surface, 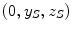.13.3 Continuous Slowing Down Approximation
13.3.1 Definition
As the name suggests, in the continuous slowing down approximation (CSDA), it is assumed that the energy loss is continuous with distance as the particle decelerates (ICRU 1984). It neglects any influence of the effects of multiple Coulomb scatter described in Chap. 6 with the result that a straight-line trajectory is assumed. Thus, for a particle with an initial kinetic energy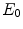 
, the CSDA range is given by
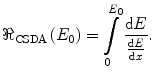
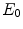, the CSDA range is given by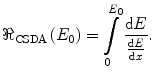(13.1)
Note that we have used our convention of considering the stopping power as a positive quantity. The full evaluation of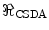 
would include the radiative energy loss contribution. However, as noted in the Preface to this book, the consideration of this contribution as being negligible is justifiable for the tissues and energy ranges of interest to medical radiation dosimetry. As 
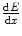is the expectation value of the rate of energy loss per unit distance through collisions, 
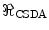represents, correspondingly, the expectation value of the particle’s range. The use of the linear collision stopping power in (13.1) yields the units of 
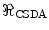as distance, whereas the use of the mass collision stopping power yields the units of mass per distance squared.
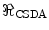would include the radiative energy loss contribution. However, as noted in the Preface to this book, the consideration of this contribution as being negligible is justifiable for the tissues and energy ranges of interest to medical radiation dosimetry. As 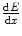is the expectation value of the rate of energy loss per unit distance through collisions, 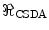represents, correspondingly, the expectation value of the particle’s range. The use of the linear collision stopping power in (13.1) yields the units of 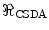as distance, whereas the use of the mass collision stopping power yields the units of mass per distance squared.13.3.2 Calculation of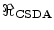 
for Heavy Charged Particles
Recall the mass collision stopping power for a massive spin-½ particle of (10.4):
![$$ \frac{{{\rm d}E}}{{\rho \mathrm{ d}x}}=2C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{\beta^2}}}{\bar{I}}} \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}+{{{\left( {\frac{1}{2}\frac{{{m_{\mathrm{ e}}}}}{{\left( {E+m} \right)}}\frac{{{\beta^2}}}{{1-{\beta^2}}}} \right)}}{^2}}} \right]. $$](/wp-content/uploads/2016/04/A306762_1_En_13_Chapter_Equ0131.gif)
Let us assume that the particle is sufficiently nonrelativistic, allowing us to neglect the last three terms within the brackets to remain with
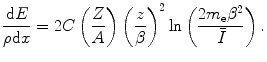
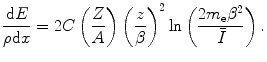
(13.2)
13.3.3 Scaling of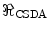 
The expression of the CSDA range given by (13.3) allows us to evaluate the CSDA range of an arbitrary heavy charged particle from that known for a reference particle. To demonstrate this, let us consider that reference particle to be a proton, in which case we will rewrite (13.3) as
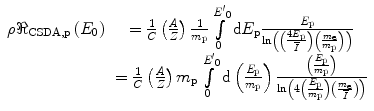
where the p subscript refers to the proton. Now consider another heavy charged particle, for which we will assign the subscript, x. Then, from (13.4),
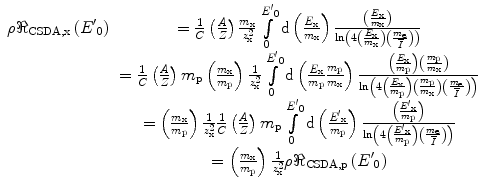
where
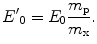
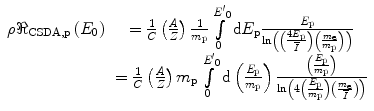
(13.4)
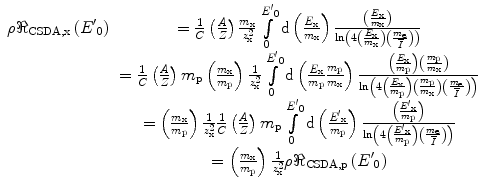
(13.5)
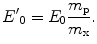
(13.6)
Thus, the CSDA range of the arbitrary charged particle can be approximated by a scaled CSDA range of a proton. For example, consider a 10-MeV α-particle where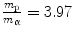 
and, from (13.6), 
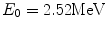. Then, from (13.5), we can estimate the CSDA range of the α
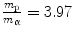and, from (13.6), 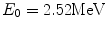. Then, from (13.5), we can estimate the CSDA range of the α
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
