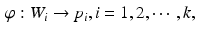, which is not necessary in our method. The elastic shape metric assumes two shapes are isotopic. However, the proposed intrinsic method is applicable for general Riemannian manifolds. Our approach solely depends on Riemannian metrics and is invariant under rigid motions and scalings such that it intrinsically measures shape distance, and thus more effective and efficient for shape classification and brain morphology analysis.
3 Theory
This section briefly introduces the theoretic foundation, for thorough treatments, we refer readers to [9] for conformal geometry, and [6, 15] for optimal mass transport theory.
3.1 Conformal Mapping
Suppose S is a topological surface, a Riemannian metric 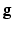 on S is a family of inner products on the tangent planes. Locally, a metric tensor is represented as a positive definite matrix
on S is a family of inner products on the tangent planes. Locally, a metric tensor is represented as a positive definite matrix 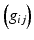 . Let
. Let 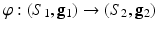 be a diffeomorphic map between two Riemannian surfaces, the pull back metric on the source induced by
be a diffeomorphic map between two Riemannian surfaces, the pull back metric on the source induced by 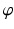 is
is 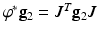 , where J is the Jacobian matrix of
, where J is the Jacobian matrix of 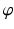 . The mapping is conformal or angle-preserving, if the pull back metric and the original metric differ by a scalar function,
. The mapping is conformal or angle-preserving, if the pull back metric and the original metric differ by a scalar function, 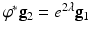 , where
, where 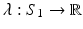 is called the conformal factor.
is called the conformal factor.
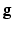 on S is a family of inner products on the tangent planes. Locally, a metric tensor is represented as a positive definite matrix
on S is a family of inner products on the tangent planes. Locally, a metric tensor is represented as a positive definite matrix 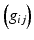 . Let
. Let 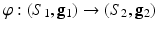 be a diffeomorphic map between two Riemannian surfaces, the pull back metric on the source induced by
be a diffeomorphic map between two Riemannian surfaces, the pull back metric on the source induced by 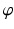 is
is 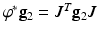 , where J is the Jacobian matrix of
, where J is the Jacobian matrix of 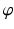 . The mapping is conformal or angle-preserving, if the pull back metric and the original metric differ by a scalar function,
. The mapping is conformal or angle-preserving, if the pull back metric and the original metric differ by a scalar function, 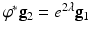 , where
, where 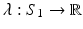 is called the conformal factor.
is called the conformal factor.Hamilton’s surface Ricci flow conformably deforms the Riemannian metric proprotional to the curvature, such that the curvature evolves according to a non-linear heat diffusion process, and becomes constant everywhere.
Definition 1
(Surface Ricci Flow). The normalized surface Ricci flow is defined as
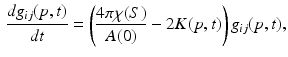 where
where 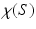 is the Euler characteristic number of the surface, A(0) is the total area at the initial time.
is the Euler characteristic number of the surface, A(0) is the total area at the initial time.
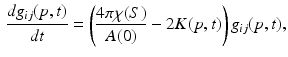
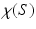 is the Euler characteristic number of the surface, A(0) is the total area at the initial time.
is the Euler characteristic number of the surface, A(0) is the total area at the initial time.Theorem 1
(Uniformization). Suppose 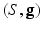 is a closed compact Riemannian surface with genus g, then there is a conformal factor function
is a closed compact Riemannian surface with genus g, then there is a conformal factor function 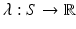 , such that the conformal metric
, such that the conformal metric 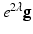 induces constant Gaussian curvature. Depending on the
induces constant Gaussian curvature. Depending on the 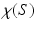 is positive, zero or negative, the const is
is positive, zero or negative, the const is 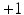 , 0 or
, 0 or 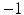 .
.
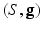 is a closed compact Riemannian surface with genus g, then there is a conformal factor function
is a closed compact Riemannian surface with genus g, then there is a conformal factor function 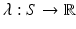 , such that the conformal metric
, such that the conformal metric 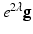 induces constant Gaussian curvature. Depending on the
induces constant Gaussian curvature. Depending on the 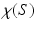 is positive, zero or negative, the const is
is positive, zero or negative, the const is 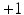 , 0 or
, 0 or 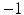 .
.In the current work, we apply surface Ricci flow to deform the human cortical surface to the unit sphere.
3.2 Optimal Mass Transport
The Optimal mass transportation problem was first raised by Monge [5] in the 18th century. Suppose 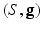 is a Riemannian manifold with a metric
is a Riemannian manifold with a metric 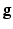 . Let
. Let 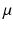 and
and 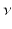 be two probability measures on S with the same total mass
be two probability measures on S with the same total mass 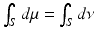 ,
, 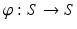 be a diffeomorphism, the pull back measure induced by
be a diffeomorphism, the pull back measure induced by 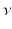 is
is 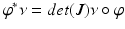 . The mapping is called measure preserving, if the pull back measure equals to the initial measure,
. The mapping is called measure preserving, if the pull back measure equals to the initial measure, 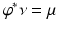 . The transportation cost of
. The transportation cost of 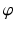 is defined as
is defined as
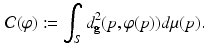
The optimal mass transportation problem is to find the measure preserving mapping, which minimizes the transportation cost,
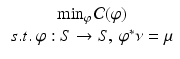 In the 1940s, Kantorovich introduced the relaxation of Monge’s problem and solved it using linear programming method [15].
In the 1940s, Kantorovich introduced the relaxation of Monge’s problem and solved it using linear programming method [15].
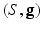 is a Riemannian manifold with a metric
is a Riemannian manifold with a metric 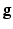 . Let
. Let 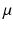 and
and 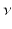 be two probability measures on S with the same total mass
be two probability measures on S with the same total mass 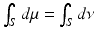 ,
, 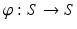 be a diffeomorphism, the pull back measure induced by
be a diffeomorphism, the pull back measure induced by 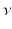 is
is 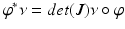 . The mapping is called measure preserving, if the pull back measure equals to the initial measure,
. The mapping is called measure preserving, if the pull back measure equals to the initial measure, 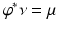 . The transportation cost of
. The transportation cost of 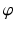 is defined as
is defined as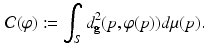
(1)
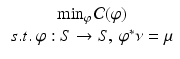
Theorem 2
(Kantorovich). Suppose 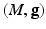 is a Riemannian manifold, probability measures
is a Riemannian manifold, probability measures 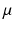 and
and 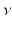 have the same total mass,
have the same total mass, 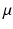 is absolutely continuous,
is absolutely continuous, 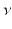 has finite second moment, the cost function is the squared geodesic distance, then the optimal mass transportation map exists and is unique.
has finite second moment, the cost function is the squared geodesic distance, then the optimal mass transportation map exists and is unique.
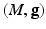 is a Riemannian manifold, probability measures
is a Riemannian manifold, probability measures 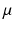 and
and 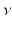 have the same total mass,
have the same total mass, 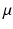 is absolutely continuous,
is absolutely continuous, 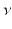 has finite second moment, the cost function is the squared geodesic distance, then the optimal mass transportation map exists and is unique.
has finite second moment, the cost function is the squared geodesic distance, then the optimal mass transportation map exists and is unique.If 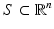 is a convex domain in the Euclidean space, then Brenier proved the following theorem.
is a convex domain in the Euclidean space, then Brenier proved the following theorem.
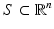 is a convex domain in the Euclidean space, then Brenier proved the following theorem.
is a convex domain in the Euclidean space, then Brenier proved the following theorem.Theorem 3
(Brenier). There is a convex function 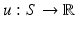 , the optimal map is given by the gradient map
, the optimal map is given by the gradient map 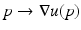 .
.
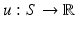 , the optimal map is given by the gradient map
, the optimal map is given by the gradient map 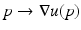 .
.Solving the optimal transportation problem is equivalent to solve the following Monge-Amperé equation,
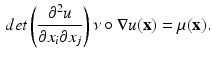
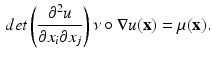
3.3 Wasserstein Metric Space
Suppose 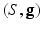 is a Riemannian manifold with a Riemannian metric
is a Riemannian manifold with a Riemannian metric 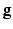 .
.
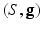 is a Riemannian manifold with a Riemannian metric
is a Riemannian manifold with a Riemannian metric 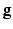 .
.Definition 2
(Wasserstein Space). For 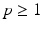 , let
, let 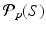 denote the space of all probability measures
denote the space of all probability measures 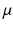 on M with finite
on M with finite 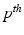 moment, for some
moment, for some 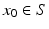 ,
, 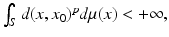 where d is the geodesic distance induced by
where d is the geodesic distance induced by 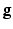 .
.
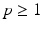 , let
, let 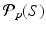 denote the space of all probability measures
denote the space of all probability measures 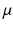 on M with finite
on M with finite 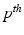 moment, for some
moment, for some 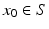 ,
, 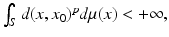 where d is the geodesic distance induced by
where d is the geodesic distance induced by 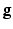 .
.Given two probability 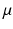 and
and 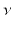 in
in 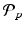 , the Wasserstein distance between them is defined as the transportation cost induced by the optimal transportation map
, the Wasserstein distance between them is defined as the transportation cost induced by the optimal transportation map 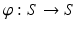 ,
,
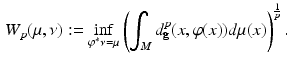 The following theorem plays a fundamental role for the current work
The following theorem plays a fundamental role for the current work
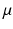 and
and 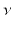 in
in 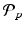 , the Wasserstein distance between them is defined as the transportation cost induced by the optimal transportation map
, the Wasserstein distance between them is defined as the transportation cost induced by the optimal transportation map 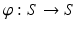 ,
,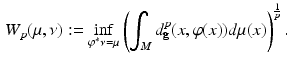
Theorem 4
The Wasserstein distance 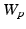 is a Riemannian metric of the Wasserstein space
is a Riemannian metric of the Wasserstein space 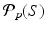 .
.
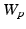 is a Riemannian metric of the Wasserstein space
is a Riemannian metric of the Wasserstein space 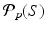 .
.Detailed proof can be found in [28].
3.4 Discrete Optimal Mass Transport
Let 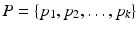 be a discrete point set on S,
be a discrete point set on S, 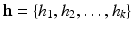 be the weight vector.
be the weight vector.
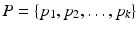 be a discrete point set on S,
be a discrete point set on S, 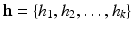 be the weight vector.
be the weight vector.Definition 3
(Geodesic Power Voronoi Diagram). Given the point set P and the weight 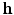 , the geodesic power voronoi diagram induced by
, the geodesic power voronoi diagram induced by 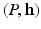 is a cell decomposition of the manifold
is a cell decomposition of the manifold 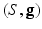 , such that the cell associated with
, such that the cell associated with 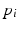 is given by
is given by
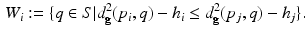
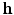 , the geodesic power voronoi diagram induced by
, the geodesic power voronoi diagram induced by 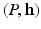 is a cell decomposition of the manifold
is a cell decomposition of the manifold 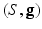 , such that the cell associated with
, such that the cell associated with 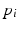 is given by
is given by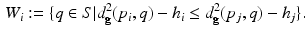
Theorem 5
(Discrete Optimal Mass Transportation Map). Given a Riemannian manifold 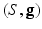 , two probability measures
, two probability measures 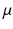 and
and 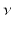 are of the same total mass.
are of the same total mass. 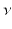 is a Dirac measure, with discrete point set support
is a Dirac measure, with discrete point set support 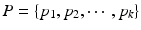 ,
, 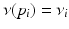 . There exists a weight
. There exists a weight 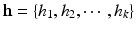 , unique up to a constant, the geodesic power Voronoi diagram induced by
, unique up to a constant, the geodesic power Voronoi diagram induced by 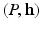 gives the optimal mass transportation map,
gives the optimal mass transportation map,
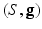 , two probability measures
, two probability measures 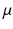 and
and 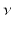 are of the same total mass.
are of the same total mass. 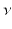 is a Dirac measure, with discrete point set support
is a Dirac measure, with discrete point set support 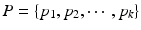 ,
, 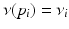 . There exists a weight
. There exists a weight 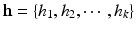 , unique up to a constant, the geodesic power Voronoi diagram induced by
, unique up to a constant, the geodesic power Voronoi diagram induced by 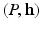 gives the optimal mass transportation map,
gives the optimal mass transportation map,