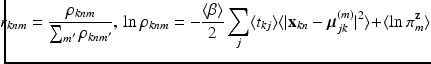Fig. 1.
The graphical representation of the proposed model; shaded and hollow circles represent observed and latent variables, respectively, arrows imply the dependencies and plates embrace numbered incidences of events.
2 Methods
2.1 Probabilistic Generative Model
Our observation consists of K point sets, denoted as 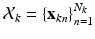 ,
,  , where
, where 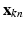 is a D dimensional feature vector corresponding to the nth landmark in the kth point set. The model can be explained as two interacting layers of mixture models. In the first (lower-dimension) layer,
is a D dimensional feature vector corresponding to the nth landmark in the kth point set. The model can be explained as two interacting layers of mixture models. In the first (lower-dimension) layer, 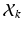 is assumed to be a collection of D-dimensional samples from a GMM with M Gaussian components. Meanwhile, by concatenating the means of the GMM (with a consistent order), a vector representation for
is assumed to be a collection of D-dimensional samples from a GMM with M Gaussian components. Meanwhile, by concatenating the means of the GMM (with a consistent order), a vector representation for 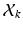 can be derived in
can be derived in 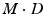 dimension. Clustering and linear component analysis for
dimension. Clustering and linear component analysis for 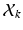 takes place in this space.
takes place in this space.
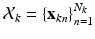 ,
, 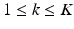 , where
, where 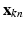 is a D dimensional feature vector corresponding to the nth landmark in the kth point set. The model can be explained as two interacting layers of mixture models. In the first (lower-dimension) layer,
is a D dimensional feature vector corresponding to the nth landmark in the kth point set. The model can be explained as two interacting layers of mixture models. In the first (lower-dimension) layer, 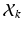 is assumed to be a collection of D-dimensional samples from a GMM with M Gaussian components. Meanwhile, by concatenating the means of the GMM (with a consistent order), a vector representation for
is assumed to be a collection of D-dimensional samples from a GMM with M Gaussian components. Meanwhile, by concatenating the means of the GMM (with a consistent order), a vector representation for 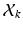 can be derived in
can be derived in 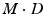 dimension. Clustering and linear component analysis for
dimension. Clustering and linear component analysis for 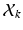 takes place in this space.
takes place in this space.More specifically, we consider a mixture of J probabilistic principal component analyzers (MPPCA). A PPCA is essentially an 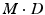 -dimensional Gaussian specified by a mean vector,
-dimensional Gaussian specified by a mean vector, 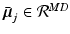 ,
, 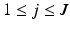 , and a covariance matrix having a subspace component in the form of
, and a covariance matrix having a subspace component in the form of 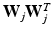 [13]. Here,
[13]. Here, 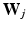 is a
is a 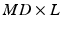 dimensional matrix, whose column l, i.e.
dimensional matrix, whose column l, i.e. 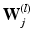 , represents one mode of variation for the cluster j. Let
, represents one mode of variation for the cluster j. Let 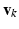 be an L dimensional vector of loading coefficients corresponding to
be an L dimensional vector of loading coefficients corresponding to 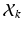 and let us define:
and let us define: 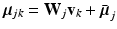 . These vectors can be thought of as variables that bridge the two layers of our model: In the higher dimension,
. These vectors can be thought of as variables that bridge the two layers of our model: In the higher dimension, 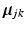 is a re-sampled representation of
is a re-sampled representation of 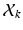 in the space spanned by principal components of the jth cluster; meanwhile, if we partition
in the space spanned by principal components of the jth cluster; meanwhile, if we partition 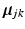 into a series of M subsequent vectors, and denote each as
into a series of M subsequent vectors, and denote each as 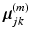 , we obtain the means of D dimensional Gaussians of the corresponding GMM.
, we obtain the means of D dimensional Gaussians of the corresponding GMM.
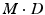 -dimensional Gaussian specified by a mean vector,
-dimensional Gaussian specified by a mean vector, 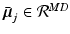 ,
, 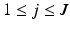 , and a covariance matrix having a subspace component in the form of
, and a covariance matrix having a subspace component in the form of 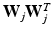 [13]. Here,
[13]. Here, 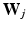 is a
is a 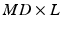 dimensional matrix, whose column l, i.e.
dimensional matrix, whose column l, i.e. 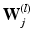 , represents one mode of variation for the cluster j. Let
, represents one mode of variation for the cluster j. Let 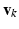 be an L dimensional vector of loading coefficients corresponding to
be an L dimensional vector of loading coefficients corresponding to 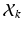 and let us define:
and let us define: 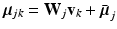 . These vectors can be thought of as variables that bridge the two layers of our model: In the higher dimension,
. These vectors can be thought of as variables that bridge the two layers of our model: In the higher dimension, 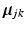 is a re-sampled representation of
is a re-sampled representation of 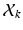 in the space spanned by principal components of the jth cluster; meanwhile, if we partition
in the space spanned by principal components of the jth cluster; meanwhile, if we partition 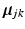 into a series of M subsequent vectors, and denote each as
into a series of M subsequent vectors, and denote each as 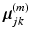 , we obtain the means of D dimensional Gaussians of the corresponding GMM.
, we obtain the means of D dimensional Gaussians of the corresponding GMM.Let 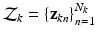 be a set of
be a set of 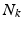 , 1-of-M coded latent membership vectors for the points in
, 1-of-M coded latent membership vectors for the points in 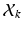 . Each
. Each 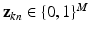 is a vector of zeros, whose mth component equals one (
is a vector of zeros, whose mth component equals one (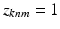 ) indicates that
) indicates that 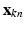 is a sample from the D dimensional Gaussian m. The precision (inverse of the variance) of Gaussians is globally denoted by
is a sample from the D dimensional Gaussian m. The precision (inverse of the variance) of Gaussians is globally denoted by 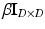 . Similarly, let
. Similarly, let 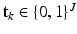 be a latent, 1-of-J coded vector whose component j being one (
be a latent, 1-of-J coded vector whose component j being one (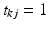 ) indicates the membership of the
) indicates the membership of the 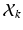 to cluster j. The conditional pdf of
to cluster j. The conditional pdf of 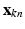 is then given by:
is then given by:
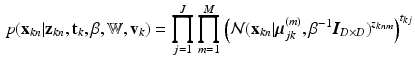
where 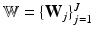 is the set of principal component matrices. To facilitate our derivations, we introduce the following prior distributions over
is the set of principal component matrices. To facilitate our derivations, we introduce the following prior distributions over 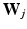 ,
, 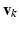 , and
, and 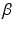 , which are conjugate to the normal distribution in Eq. (1):
, which are conjugate to the normal distribution in Eq. (1):
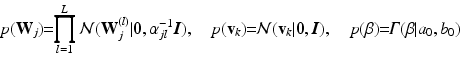
The hyper-parameters of the Gamma distribution in the last line are set to 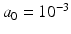 and
and 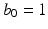 to have a flat prior over
to have a flat prior over 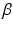 . Next, we respectively denote the mixture weights of GMMs and MPPCA by
. Next, we respectively denote the mixture weights of GMMs and MPPCA by 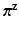 and
and 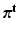 vectors, each having a Dirichlet distribution as priors:
vectors, each having a Dirichlet distribution as priors: 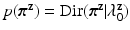 ,
, 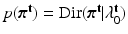 . where we set
. where we set 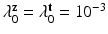 . The conditional distributions of membership vectors of
. The conditional distributions of membership vectors of 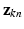 (for points) and
(for points) and 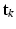 (for point sets) given mixing weights are specified by two multi-nomial distributions:
(for point sets) given mixing weights are specified by two multi-nomial distributions: 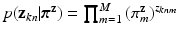 , and
, and 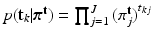 , where
, where 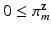 ,
, 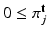 are the components m, j of
are the components m, j of 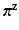 ,
, 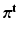 , respectively. We now construct the joint pdf of the sets of all random variables, by assuming (conditional) independence and multiplying the pdfs where needed. Let
, respectively. We now construct the joint pdf of the sets of all random variables, by assuming (conditional) independence and multiplying the pdfs where needed. Let 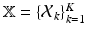 ,
, 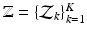 ,
, 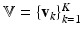 , and
, and 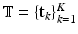 , then the distributions of these variables can be written as:
, then the distributions of these variables can be written as:
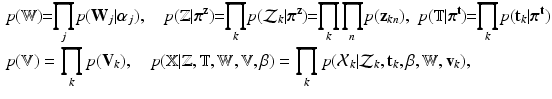
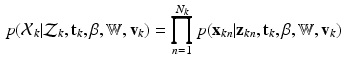
Having defined the required distributions through Eqs. (1)-(3), the distribution of the complete observation is given as
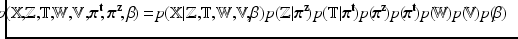
Figure 1 is a graphical representation for the generative model considered in this paper. Given observations (colored dark gray) as D dimensional points, our problem is to estimate the posterior distributions of all the latent random variables (hollow circles) and hyper-parameters, which include the discrete cluster and the continuous variables (e.g. means and modes of variations).
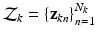 be a set of
be a set of 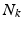 , 1-of-M coded latent membership vectors for the points in
, 1-of-M coded latent membership vectors for the points in 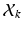 . Each
. Each 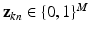 is a vector of zeros, whose mth component equals one (
is a vector of zeros, whose mth component equals one (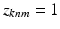 ) indicates that
) indicates that 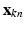 is a sample from the D dimensional Gaussian m. The precision (inverse of the variance) of Gaussians is globally denoted by
is a sample from the D dimensional Gaussian m. The precision (inverse of the variance) of Gaussians is globally denoted by 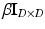 . Similarly, let
. Similarly, let 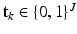 be a latent, 1-of-J coded vector whose component j being one (
be a latent, 1-of-J coded vector whose component j being one (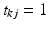 ) indicates the membership of the
) indicates the membership of the 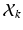 to cluster j. The conditional pdf of
to cluster j. The conditional pdf of 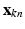 is then given by:
is then given by: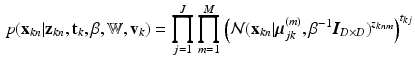
(1)
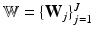 is the set of principal component matrices. To facilitate our derivations, we introduce the following prior distributions over
is the set of principal component matrices. To facilitate our derivations, we introduce the following prior distributions over 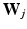 ,
, 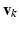 , and
, and 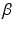 , which are conjugate to the normal distribution in Eq. (1):
, which are conjugate to the normal distribution in Eq. (1):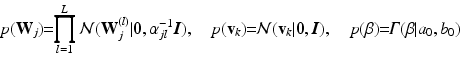
(2)
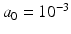 and
and 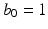 to have a flat prior over
to have a flat prior over 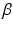 . Next, we respectively denote the mixture weights of GMMs and MPPCA by
. Next, we respectively denote the mixture weights of GMMs and MPPCA by 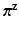 and
and 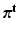 vectors, each having a Dirichlet distribution as priors:
vectors, each having a Dirichlet distribution as priors: 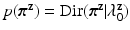 ,
, 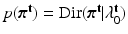 . where we set
. where we set 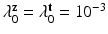 . The conditional distributions of membership vectors of
. The conditional distributions of membership vectors of 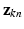 (for points) and
(for points) and 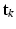 (for point sets) given mixing weights are specified by two multi-nomial distributions:
(for point sets) given mixing weights are specified by two multi-nomial distributions: 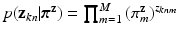 , and
, and 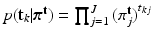 , where
, where 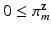 ,
, 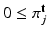 are the components m, j of
are the components m, j of 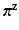 ,
, 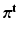 , respectively. We now construct the joint pdf of the sets of all random variables, by assuming (conditional) independence and multiplying the pdfs where needed. Let
, respectively. We now construct the joint pdf of the sets of all random variables, by assuming (conditional) independence and multiplying the pdfs where needed. Let 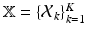 ,
, 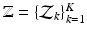 ,
, 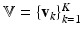 , and
, and 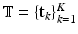 , then the distributions of these variables can be written as:
, then the distributions of these variables can be written as: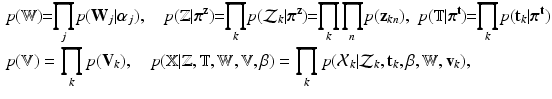
(3)
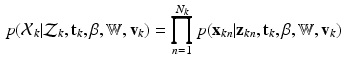
(4)
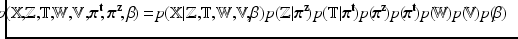
(5)
2.2 Approximated Inference
If we denote the set of latent variables as 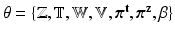 , direct inference of
, direct inference of 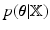 (as our objective) is analytically intractable thus an approximated distribution,
(as our objective) is analytically intractable thus an approximated distribution, 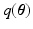 , is sought. Owing to the dimensionality of the data, we prefer Variational Bayes (VB) over sampling based methods. The VB principle for obtaining
, is sought. Owing to the dimensionality of the data, we prefer Variational Bayes (VB) over sampling based methods. The VB principle for obtaining 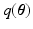 is explained briefly. The model evidence, i.e.
is explained briefly. The model evidence, i.e. 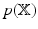 1, can be decomposed as
1, can be decomposed as 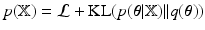 , where
, where 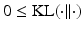 denotes the Kullback-Leilber divergence, and
denotes the Kullback-Leilber divergence, and
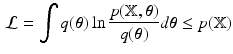
is a lower bound on 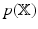 . To obtain
. To obtain 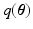 , the
, the 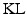 divergence between the true and the approximated posterior should be minimized. However, this is not feasible because the true posterior is not accessible to us. Thus,
divergence between the true and the approximated posterior should be minimized. However, this is not feasible because the true posterior is not accessible to us. Thus, 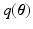 can be computed by maximizing
can be computed by maximizing 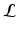 . We approximate the true posterior as a factorized form, i.e.,
. We approximate the true posterior as a factorized form, i.e., 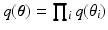 , where
, where 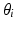 refers to any of our latent variables. This factorization leads to the following tractable result: let
refers to any of our latent variables. This factorization leads to the following tractable result: let 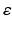 be the variable of interest in
be the variable of interest in 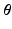 , and
, and 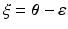 , then the variational posterior of
, then the variational posterior of 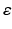 is given by
is given by 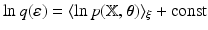 , where
, where 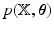 is given in Eq. (5),
is given in Eq. (5), 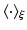 denotes the expectation w.r.t. to the product of
denotes the expectation w.r.t. to the product of 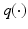 of all variable in
of all variable in 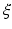 .
.
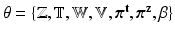 , direct inference of
, direct inference of 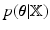 (as our objective) is analytically intractable thus an approximated distribution,
(as our objective) is analytically intractable thus an approximated distribution, 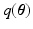 , is sought. Owing to the dimensionality of the data, we prefer Variational Bayes (VB) over sampling based methods. The VB principle for obtaining
, is sought. Owing to the dimensionality of the data, we prefer Variational Bayes (VB) over sampling based methods. The VB principle for obtaining 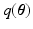 is explained briefly. The model evidence, i.e.
is explained briefly. The model evidence, i.e. 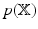 1, can be decomposed as
1, can be decomposed as 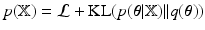 , where
, where 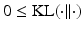 denotes the Kullback-Leilber divergence, and
denotes the Kullback-Leilber divergence, and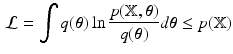
(6)
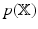 . To obtain
. To obtain 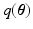 , the
, the 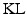 divergence between the true and the approximated posterior should be minimized. However, this is not feasible because the true posterior is not accessible to us. Thus,
divergence between the true and the approximated posterior should be minimized. However, this is not feasible because the true posterior is not accessible to us. Thus, 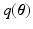 can be computed by maximizing
can be computed by maximizing 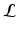 . We approximate the true posterior as a factorized form, i.e.,
. We approximate the true posterior as a factorized form, i.e., 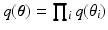 , where
, where 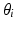 refers to any of our latent variables. This factorization leads to the following tractable result: let
refers to any of our latent variables. This factorization leads to the following tractable result: let 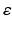 be the variable of interest in
be the variable of interest in 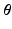 , and
, and 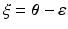 , then the variational posterior of
, then the variational posterior of 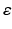 is given by
is given by 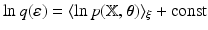 , where
, where 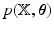 is given in Eq. (5),
is given in Eq. (5), 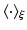 denotes the expectation w.r.t. to the product of
denotes the expectation w.r.t. to the product of 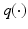 of all variable in
of all variable in 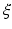 .
.2.3 Update of Posteriors and Hyper-Parameters
In this section, we provide equations to update the variational posteriors. Thanks to conjugacy of priors to likelihoods, these derivations are done by inspecting expectations of logarithms and matching posteriors to their corresponding likelihood template forms. Detailed proof of our derivations is skipped for brevity. Starting from 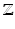 variables we have
variables we have 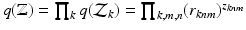 Under this equation, we have
Under this equation, we have 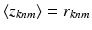 , where the right hand side can be computed using the following relationships:
, where the right hand side can be computed using the following relationships:
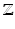 variables we have
variables we have  Under this equation, we have
Under this equation, we have 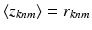 , where the right hand side can be computed using the following relationships:
, where the right hand side can be computed using the following relationships: