(1)
Amersham, Buckinghamshire, UK
Abstract
Our calculations have, to this point, been for elemental media, in particular carbon, calcium and lead (some data have been shown graphically for striated muscle, compact bone and liquid water, but these are derived from data presented elsewhere). It is necessary to take the foundation of the elemental media calculations and develop the calculations for realistic compound media. This is almost invariably done within the context of the Bragg additivity rule in which energy loss, and other physical parameters, for a compound medium is evaluated as the weighted sum of the energy losses incurred by the individual elements, with the weights being the relative proportions of these elements. There are deficiencies in such an approach as it assumes that there is no change in electronic structure as a result of bonding or with the different material phases of the medium. In this chapter, the Bragg additivity rule is derived ab initio and the practicalities of its deviations are examined and quantified.
14.1 Introductory Comments
Throughout our numerical and graphical examples given in Parts II and III, we have restricted our derivations to elemental (i.e. monatomic) media. This is deliberate as we wished to defer our exploration of compound media until we had attained a suitable foundation in understanding collision energy loss. In particular, we have used carbon and calcium as crude elemental representations of soft tissue and bone. Of course, both are, in fact, compounds and Table 14.1 summarises the fractions by weight of the atomic constituents for various tissues. Hydrogen, carbon and oxygen are the dominant constituents of soft tissues, with the addition of calcium for bone. Thus, a dosimetry calculation for tissue must be extended to account for the aggregate effects within a compound medium.
Table 14.1
Constituents of tissue: examples (as fraction by weight exceeding 0.001)
Z = | Hydrogen | Carbon | Nitrogen | Oxygen | Sodium | Magnesium | Phosphorus | Sulphur | Chlorine | Potassium | Calcium | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Tissue | ρ (g/cm3) | 1 | 6 | 7 | 8 | 11 | 12 | 15 | 16 | 17 | 19 | 20 |
Adipose tissue (ICRP) | 0.92 | 0.119 | 0.637 | 0.008 | 0.232 | – | – | – | – | 0.001 | – | – |
Bone, cortical (ICRP) | 1.85 | 0.047 | 0.144 | 0.042 | 0.446 | – | 0.002 | 0.105 | 0.003 | – | – | 0.210 |
Muscle, skeletal (ICRP) | 1.04 | 0.101 | 0.108 | 0.028 | 0.754 | 0.001 | – | 0.002 | 0.002 | 0.001 | 0.003 | – |
Muscle, striated (ICRP) | 1.04 | 0.102 | 0.123 | 0.035 | 0.729 | 0.001 | – | 0.002 | 0.005 | – | 0.003 | – |
The most commonly used method of calculating the stopping power of a compound medium is to approximate it by a weighted linear sum of the stopping powers of the elemental constituents. This approximation is known as the Bragg additivity rule. It is reasonably accurate in that it has been reported capable of reproducing measured stopping power data in compound media to within about 20 % (although literature reviews, cited below, indicate that the uncertainties can approach 50 % in some cases). As expected by the values quoted in the previous sentence, the validity of the rule has been studied in numerous cases, but the relative discrepancies between the actual stopping power in a compound medium and that calculated by the rule from elemental data can vary widely, leading frequently to confusion in some applications.
The accuracy of the Bragg additivity rule will be limited as the collision stopping power in a medium is dependent upon the atomic electrons’ orbital structures and excitation channels. As these will vary, not only with the nature of chemical bonding, but also with the phase of the medium, it is not at all surprising that the assumption inherent to the rule – that the electronic structures of the elements remain unaltered when a compound is formed – leads to inaccuracies. Thwaites (1983, 1992) has surveyed the relevant literature up to those dates and reviewed over 100 studies of the Bragg additivity rule and concluded that inaccuracies in the rule were most prominent for low atomic number media (hydrocarbons) at low charged particle kinetic energies . For such combinations, deviations as great as 50 % can occur. However, at the same time, the accuracies of stopping power measurements at these energies are also limited, thus making assessments of the failure of the Bragg additivity rule somewhat ambiguous.
In this chapter, we will derive the Bragg additivity rule from first principles and then investigate its applications in calculating the mean excitation potential, the effective ratio of atomic number to atomic mass number and the density correction parameter for a compound medium. In the specific context of the mean excitation potential, we will consider explicit means of assigning values for hydrocarbons on the basis of the structures of the chemical bonds.
14.2 The Bragg Additivity Rule
14.2.1 Derivation
Bragg and Kleeman (1905) proposed a means of calculating for the effects of a compound medium upon an energetic charged particle based upon the individual constituents. This proposal evolved out of their experimental studies of the stopping of α-particles in the hydrocarbon–halogen gases of CH3Br and CH3I in which they investigated this stopping as a function of atomic number. They isolated the stopping in iodine and bromine by subtracting the stopping contributions of carbon and hydrogen in these compounds using the stopping powers evaluated separately in pure carbon and hydrogen targets. They concluded that the stopping power in a compound can be estimated by the mass-weighted linear sum of the stopping powers of the individual atomic constituents.
We can derive the Bragg additivity rule for collision energy losses using the approach suggested by Sigmund (2006). Consider a medium composed of a mixture of n noble gases held at low pressure. In these cases, there are no bonds between the constituents and we can treat the medium as a mixture of independent elemental constituents. Then, the mean energy loss of a charged particle traversing a thickness 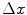 of this medium is
of this medium is
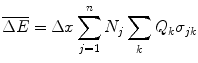
where N j is the number of atoms of the jth noble gas per unit volume, Q k




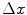 of this medium is
of this medium is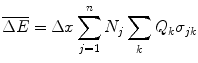
(14.1)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree