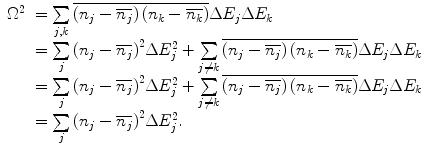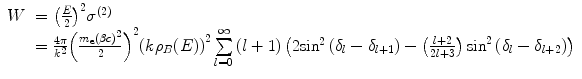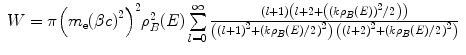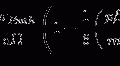(1)
Amersham, Buckinghamshire, UK
Abstract
Here, the statistical metrics used in the description of stochastic energy loss (or energy straggling) are derived. The stopping cross section has been previously derived and is the first moment of collision energy loss/transfer. Higher-order moments will be required in descriptions of the statistical nature of collision energy loss. Clearly, the first to be derived will be the second moment as this is necessary for the derivation of the variance of the probability distribution function. The derivation of the third moment will be deferred to Chap 18 when it is properly developed in the context of asymmetric collision energy loss probability distribution functions. The straggling parameter, a contributor to the second moment, is derived as is that due to Bohr. Finally, the effects of a condensed medium upon energy straggling are considered.
16.1 Introductory Notes
While in the subsequent chapters we will deal with specific statistical models of energy lost, this chapter is concerned with the general statistical description of energy loss, or energy straggling . This will lead to a focus on the width of the energy loss pdf, characterised by either its variance or the straggling parameter.
In the discussion presented in this chapter, it will be assumed initially that the collision events follow the Poisson distribution with the interactions being statistically independent, as this allows a considerable simplification in the calculation of the width of the pdf. This simplification is based upon the assumption that projectile–atom collisions resulting in different energy transfers are statistically independent due to a wide separation between the atoms of a medium. Such an assumption is appropriate for the dilute medium, such as a gas, that we have used frequently in earlier derivations. However, the validity of this assumption comes into question should the energetic charged particle be traversing a medium for which the atomic separations are much reduced.
The chapter begins with the definition of the mean energy loss on the basis of a statistical description founded on the stopping cross section, a quantity we have made much use of in the past. It then considers the mean-squared energy loss and the variance of the energy loss pdf and the definition of the straggling parameter. This latter quantity is then explored further through classical (Bohr) and quantum mechanical (Bethe) means. The chapter concludes with an examination of the effects of the density of the medium upon the straggling parameter where the correlations between projectile–atom collisions must be accounted for.
16.2 Stochastic Descriptions of Energy Loss
16.2.1 Stopping Cross Section and Straggling Parameter
Consider a charged particle with kinetic energy E traversing a medium. Over a given path length of the medium, considered to be shorter than the complete range of the particle in that medium, the net energy loss is given by the summation of the energy losses that occur during the discrete interactions between that particle and the atoms of the medium:
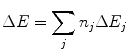
where 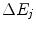 is the energy transferred from the projectile to an atom during a collision of the type j and n j is the number of interactions of that type. Note that as
is the energy transferred from the projectile to an atom during a collision of the type j and n j is the number of interactions of that type. Note that as 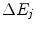 is the energy transfer resulting from a single collision,
is the energy transfer resulting from a single collision, 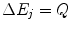 . The mean collision energy loss over this path length is averaged over this number of interactions :
. The mean collision energy loss over this path length is averaged over this number of interactions :
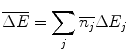
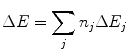
(16.1)
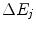 is the energy transferred from the projectile to an atom during a collision of the type j and n j is the number of interactions of that type. Note that as
is the energy transferred from the projectile to an atom during a collision of the type j and n j is the number of interactions of that type. Note that as 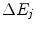 is the energy transfer resulting from a single collision,
is the energy transfer resulting from a single collision, 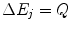 . The mean collision energy loss over this path length is averaged over this number of interactions :
. The mean collision energy loss over this path length is averaged over this number of interactions :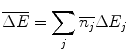
(16.2)
Obviously, the mean number of interactions is
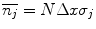
where N is again the number density of scattering centres in the medium, Δx is the thickness of the medium in which the interactions occur and σ j is the total cross section for the jth interaction type. From the definition of the linear collision stopping power (in a finite consideration), we have
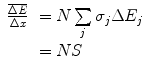
where the stopping cross section, S, of (8.85) has been written in the discrete sense. The variance of the energy loss is, by definition ,
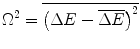
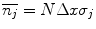
(16.3)
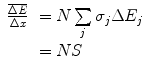
(16.4)
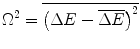
(16.5)
The fact that the summation for 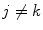 has been set equal to zero is a consequence of the assumed statistical independence of the interactions. However, from our discussions in Chaps. 8 and 12 of the interactions of charged particles in condensed media, special attention needs to be paid to the degree of validity of this assumption that atomic interactions are independent. As we shall see, energy straggling is dependent upon the material state of the medium. Accepting that this assumption is acceptable, we will further assume that Poisson statistics is valid and write the variance as
has been set equal to zero is a consequence of the assumed statistical independence of the interactions. However, from our discussions in Chaps. 8 and 12 of the interactions of charged particles in condensed media, special attention needs to be paid to the degree of validity of this assumption that atomic interactions are independent. As we shall see, energy straggling is dependent upon the material state of the medium. Accepting that this assumption is acceptable, we will further assume that Poisson statistics is valid and write the variance as
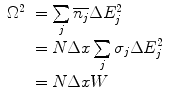
where the straggling parameter, W, has been introduced . We now rewrite the discrete representations of S of (16.4) and W of (16.7) into the continuous regime and in terms of the energy transfer in single collisions:
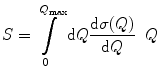
and
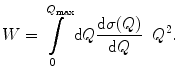
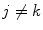 has been set equal to zero is a consequence of the assumed statistical independence of the interactions. However, from our discussions in Chaps. 8 and 12 of the interactions of charged particles in condensed media, special attention needs to be paid to the degree of validity of this assumption that atomic interactions are independent. As we shall see, energy straggling is dependent upon the material state of the medium. Accepting that this assumption is acceptable, we will further assume that Poisson statistics is valid and write the variance as
has been set equal to zero is a consequence of the assumed statistical independence of the interactions. However, from our discussions in Chaps. 8 and 12 of the interactions of charged particles in condensed media, special attention needs to be paid to the degree of validity of this assumption that atomic interactions are independent. As we shall see, energy straggling is dependent upon the material state of the medium. Accepting that this assumption is acceptable, we will further assume that Poisson statistics is valid and write the variance as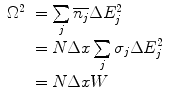
(16.7)
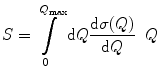
(16.8)
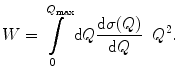
(16.9)
16.2.2 Partial Wave Derivation of the Straggling Parameter
We now call upon our earlier developments of the partial wave and phase shift analyses of Chaps. 2 and 4 and the results of Appendix C.2 to expand the expressions of (16.8) and (16.9) for the stopping cross section and straggling parameter in terms of the transport cross section introduced in Sect. 6.3.5 of Chap. 6 which describes the Goudsmit–Saunderson theory of multiple elastic Coulomb scatter. That is, we define the first- and second-order transport equations as
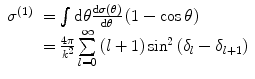
and
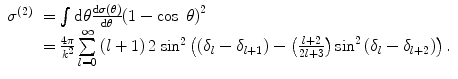
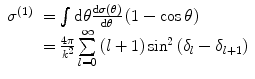
(16.10)
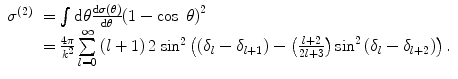
(16.11)
The fraction within the summation can be subsequently split:
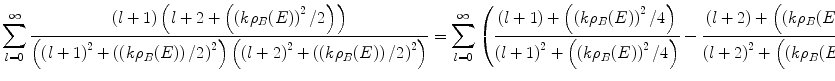
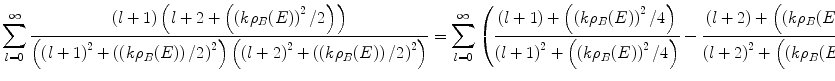
(16.14)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree