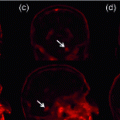
to 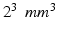 which is too large to study certain brain structures that are a few millimeters thick. Due to signal loss from
which is too large to study certain brain structures that are a few millimeters thick. Due to signal loss from 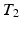 decay with longer echo times, reducing the voxel size leads to a proportionate decrease in the signal-to-noise ratio (SNR). Though SNR could be enhanced by averaging multiple acquisitions, the total acquisition time may be too long to apply this approach in clinical settings.
decay with longer echo times, reducing the voxel size leads to a proportionate decrease in the signal-to-noise ratio (SNR). Though SNR could be enhanced by averaging multiple acquisitions, the total acquisition time may be too long to apply this approach in clinical settings.
Existing techniques that obtain high-resolution (HR) dMRI can be classified into two categories based on their data acquisition scheme. The first group of methods obtain HR data using a single LR image via intelligent interpolations or regularizations. These types of methods have been investigated in structural MRI [2] and in dMRI to enhance anatomical details as in [3]. However, as pointed out in [3], the performance of some of these methods still largely relies on the information contained in the original LR image. The second group of methods require multiple LR images acquired according to a specific sampling scheme to reconstruct a HR image. Each of the LR image is modeled as the measurement of an underlying HR image via a down-sampling operator. Then the HR image is estimated by solving a linear inverse problem with suitable regularization. These methods use the classical concept of super-resolution reconstruction (SRR) [4]. In dMRI, these methods were used in [5, 6] to reconstruct each diffusion weighted volume independently. A different acquisition scheme with the LR images having orthogonal slice acquisition direction was proposed in [7]. However, the distortions from LR scans with different slice directions need to be corrected prior to applying the SRR algorithm, which involves complex non-linear spatial normalization. Moreover, each diffusion-weighted image (DWI) volume is reconstructed independently, requiring the LR images to be acquired or interpolated on the same dense set of gradient directions. Thus, these methods require the same number of measurements (e.g., 60 gradient directions) for each LR acquisition. To address this problem, more recently, [8] introduced a method that used the diffusion tensor imaging (DTI) technique to model the diffusion signal in q-space. However, a very simplistic diffusion tensor model was assumed, which is not appropriate for modeling more complex diffusion phenomena (crossing fibers). A similar method has been proposed in [9] to improve distortion corrections for DWI’s using interlaced q-space sampling.
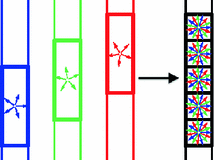

Fig. 1.
An illustration of the CS-SRR scheme: a high-resolution image is reconstructed using three overlapping thick-slice volumes with down-sampled diffusion directions.
Our Contributions: We propose a compressed-sensing-based super-resolution reconstruction (CS-SRR) approach for reconstructing HR diffusion images from multiple sub-pixel-shifted thick-slice acquisitions. As illustrated in Fig. 1, we use three LR images with anisotropic voxel sizes that are shifted in the slice acquisition direction. Each LR image is acquired with a different (unique) set of gradient directions to construct a single HR image with isotropic voxel size and a combined set of gradient directions. This is in contrast to classical SRR techniques which require each LR scan to have the same set of gradient directions. In the proposed framework, only a subset (one-third) of the total number of gradient directions are acquired for each LR scan, which reduces scan time significantly while making the technique robust to head motion. To account for the correlation between diffusion signal along different gradients, we represent the signal in the HR image in a sparsifying basis of spherical ridgelets. To obtain the HR image, we propose a framework based on the ADMM algorithm, where we enforce sparsity in the spherical-ridgelet domain and spatial consistency using total variation regularization. We perform quantitative validation of our technique using very high resolution data acquired on a clinical 3 T scanner.
2 Background
We consider diffusion images acquired on single spherical shell in q-space [10]. Hence, the problem of super resolution reduces to that of reconstructing the spherical signal at each voxel of the HR image. Before introducing the proposed method, we provide a brief note on the concepts of compressed sensing and spherical ridgelets that are used to model and estimate the diffusion signals.
Compressed Sensing: The theory of compressed sensing provides the mathematical foundation for accurate recovery of signals from set of measurements far fewer than that required by the Nyquist criteria [11]. In the CS framework, a signal of interest 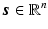 is represented in an over-complete basis
is represented in an over-complete basis 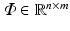 with
with 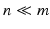 such that
such that 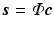 with
with 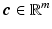 being a sparse vector, i.e.
being a sparse vector, i.e. 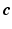 only has few non-zero elements. Let
only has few non-zero elements. Let 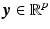 denote a measurement vector given by
denote a measurement vector given by 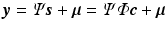 where
where 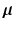 is the noise component and
is the noise component and 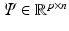 is a down-sampling operator. If the matrix
is a down-sampling operator. If the matrix 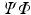 satisfies certain incoherent properties, then the CS theory [11] asserts that the sparse vector
satisfies certain incoherent properties, then the CS theory [11] asserts that the sparse vector 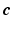 can be robustly recovered by solving the
can be robustly recovered by solving the 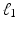 -norm regularized problem
-norm regularized problem
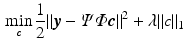
for a suitable 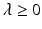 . Hence, the signal
. Hence, the signal 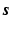 can be accurately recovered as
can be accurately recovered as 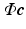 using the lower dimensional measurement
using the lower dimensional measurement 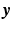 . This CS methodology has been used to estimate the dMRI signal from reduced number of measurements [12–14] with the basis given by the spherical ridgelets.
. This CS methodology has been used to estimate the dMRI signal from reduced number of measurements [12–14] with the basis given by the spherical ridgelets.
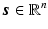 is represented in an over-complete basis
is represented in an over-complete basis 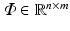 with
with 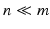 such that
such that 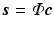 with
with 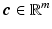 being a sparse vector, i.e.
being a sparse vector, i.e. 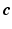 only has few non-zero elements. Let
only has few non-zero elements. Let 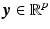 denote a measurement vector given by
denote a measurement vector given by 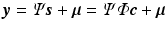 where
where 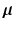 is the noise component and
is the noise component and 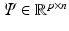 is a down-sampling operator. If the matrix
is a down-sampling operator. If the matrix 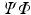 satisfies certain incoherent properties, then the CS theory [11] asserts that the sparse vector
satisfies certain incoherent properties, then the CS theory [11] asserts that the sparse vector 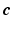 can be robustly recovered by solving the
can be robustly recovered by solving the 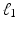 -norm regularized problem
-norm regularized problem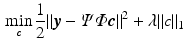
(1)
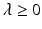 . Hence, the signal
. Hence, the signal 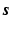 can be accurately recovered as
can be accurately recovered as 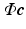 using the lower dimensional measurement
using the lower dimensional measurement 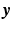 . This CS methodology has been used to estimate the dMRI signal from reduced number of measurements [12–14] with the basis given by the spherical ridgelets.
. This CS methodology has been used to estimate the dMRI signal from reduced number of measurements [12–14] with the basis given by the spherical ridgelets.Spherical Ridgelets: Spherical ridgelet functions were introduced in [12] as a frame to represent 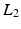 functions on the sphere. Each spherical ridgelet function is specially designed to represent diffusion signals with a particular orientation and certain degree of anisotropy. A sparse combination of such basis functions is suitable to model the diffusion data with complex fiber orientations [13, 14]. Specifically, the spherical ridgelets are constructed as follows: For
functions on the sphere. Each spherical ridgelet function is specially designed to represent diffusion signals with a particular orientation and certain degree of anisotropy. A sparse combination of such basis functions is suitable to model the diffusion data with complex fiber orientations [13, 14]. Specifically, the spherical ridgelets are constructed as follows: For 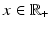 and
and 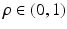 , let
, let 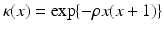 be a Gaussian function. Further, we let
be a Gaussian function. Further, we let
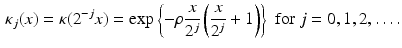 Then the spherical ridgelets with their energy spread around the great circle supported by a unit vector
Then the spherical ridgelets with their energy spread around the great circle supported by a unit vector 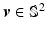 is given by
is given by
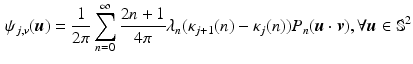
where 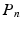 denotes the Legendre polynomial of order n,
denotes the Legendre polynomial of order n, 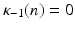 ,
, 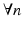 and
and 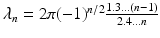 if n is even, otherwise
if n is even, otherwise 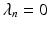 .
.
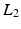 functions on the sphere. Each spherical ridgelet function is specially designed to represent diffusion signals with a particular orientation and certain degree of anisotropy. A sparse combination of such basis functions is suitable to model the diffusion data with complex fiber orientations [13, 14]. Specifically, the spherical ridgelets are constructed as follows: For
functions on the sphere. Each spherical ridgelet function is specially designed to represent diffusion signals with a particular orientation and certain degree of anisotropy. A sparse combination of such basis functions is suitable to model the diffusion data with complex fiber orientations [13, 14]. Specifically, the spherical ridgelets are constructed as follows: For 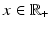 and
and 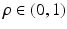 , let
, let 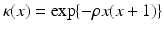 be a Gaussian function. Further, we let
be a Gaussian function. Further, we let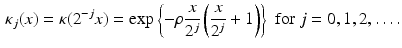
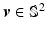 is given by
is given by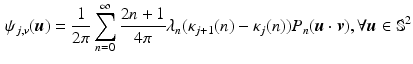
(2)
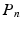 denotes the Legendre polynomial of order n,
denotes the Legendre polynomial of order n, 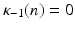 ,
, 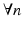 and
and 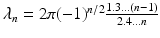 if n is even, otherwise
if n is even, otherwise 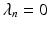 .
.To construct a finite over-complete dictionary, we follow the method in [13, 14] and restrict the values for the resolution index j to the set 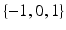 . For each resolution index j, the set of all possible orientations
. For each resolution index j, the set of all possible orientations 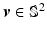 is discretized to a set of
is discretized to a set of 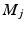 directions on the unit sphere with
directions on the unit sphere with 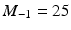 ,
, 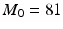 and
and 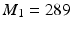 . To this end, the set of over-complete spherical ridgelets is given by
. To this end, the set of over-complete spherical ridgelets is given by 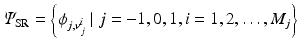 . Since the spherical ridgelets are anisotropic, the isotropic diffusion signal in the CSF areas is not efficiently modeled as a sparse combination of the basis functions. To resolve this issue, we expand the basis functions by adding one isotropic element as
. Since the spherical ridgelets are anisotropic, the isotropic diffusion signal in the CSF areas is not efficiently modeled as a sparse combination of the basis functions. To resolve this issue, we expand the basis functions by adding one isotropic element as 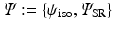 where
where 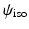 denotes a constant function on the unit sphere. For convenience, we denote the functions in
denotes a constant function on the unit sphere. For convenience, we denote the functions in 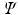 as
as 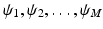 with
with 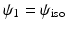 . Given the diffusion signal measured along N diffusion directions
. Given the diffusion signal measured along N diffusion directions 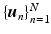 , we construct a basis matrix A with
, we construct a basis matrix A with 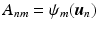 for
for 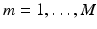 and
and 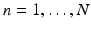 .
.
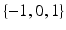 . For each resolution index j, the set of all possible orientations
. For each resolution index j, the set of all possible orientations 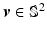 is discretized to a set of
is discretized to a set of 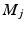 directions on the unit sphere with
directions on the unit sphere with 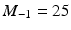 ,
, 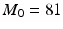 and
and 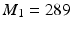 . To this end, the set of over-complete spherical ridgelets is given by
. To this end, the set of over-complete spherical ridgelets is given by 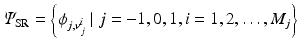 . Since the spherical ridgelets are anisotropic, the isotropic diffusion signal in the CSF areas is not efficiently modeled as a sparse combination of the basis functions. To resolve this issue, we expand the basis functions by adding one isotropic element as
. Since the spherical ridgelets are anisotropic, the isotropic diffusion signal in the CSF areas is not efficiently modeled as a sparse combination of the basis functions. To resolve this issue, we expand the basis functions by adding one isotropic element as 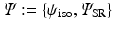 where
where 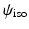 denotes a constant function on the unit sphere. For convenience, we denote the functions in
denotes a constant function on the unit sphere. For convenience, we denote the functions in 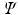 as
as 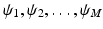 with
with 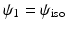 . Given the diffusion signal measured along N diffusion directions
. Given the diffusion signal measured along N diffusion directions 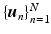 , we construct a basis matrix A with
, we construct a basis matrix A with 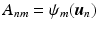 for
for 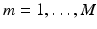 and
and 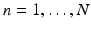 .
.3 Method
Let 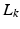 ,
, 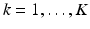 , denote the K low-resolution diffusion weighted imaging (DWI) volumes. For each
, denote the K low-resolution diffusion weighted imaging (DWI) volumes. For each 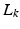 , the diffusion signal is acquired along a set of gradient directions
, the diffusion signal is acquired along a set of gradient directions 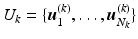 at the same b-value. The set of gradient directions for each LR image
at the same b-value. The set of gradient directions for each LR image 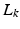 is assumed to be different, i.e.
is assumed to be different, i.e. 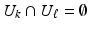 for
for 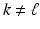 . The HR image that has
. The HR image that has 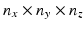 voxels and
voxels and 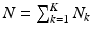 gradient directions is denoted by a matrix H of size
gradient directions is denoted by a matrix H of size 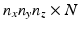 . Then, each LR image
. Then, each LR image 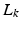 is given by
is given by
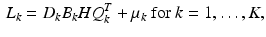
where 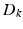 denotes the down-sampling matrix that averages neighboring slices,
denotes the down-sampling matrix that averages neighboring slices, 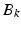 denotes the blurring (or point-spread function) and
denotes the blurring (or point-spread function) and 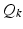 is the sub-sampling matrix in q-space. The main difference between the above model and the one used in [6, 15] is given by the
is the sub-sampling matrix in q-space. The main difference between the above model and the one used in [6, 15] is given by the 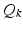 ’s that allow the LR images to have different sets of gradient directions. Further, we use the spherical ridgelets basis to model the diffusion signal at each voxel of H. To this end, H is assumed to satisfy
’s that allow the LR images to have different sets of gradient directions. Further, we use the spherical ridgelets basis to model the diffusion signal at each voxel of H. To this end, H is assumed to satisfy 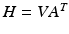 with A being the basis matrix of spherical ridgelets (SR) constructed along the set of gradient directions
with A being the basis matrix of spherical ridgelets (SR) constructed along the set of gradient directions 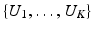 and each row vector of V being the SR coefficients at the corresponding voxel. Since each basis function is designed to model a diffusion signal with certain degree of anisotropy, a non-negative combination of spherical ridgelets provides more robust representation for diffusion signals especially when the SNR is low. Hence, the coefficients V are restricted to be non-negative. Following (1), we estimate H by solving
and each row vector of V being the SR coefficients at the corresponding voxel. Since each basis function is designed to model a diffusion signal with certain degree of anisotropy, a non-negative combination of spherical ridgelets provides more robust representation for diffusion signals especially when the SNR is low. Hence, the coefficients V are restricted to be non-negative. Following (1), we estimate H by solving
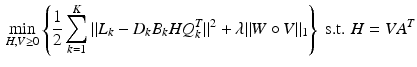
where 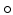 denotes the element-wise multiplication,
denotes the element-wise multiplication, 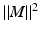 is the squared Frobenius norm of a matrix M and
is the squared Frobenius norm of a matrix M and 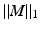 is the summation of the absolute values of all the entries of M. W is the weighting matrix with each row having the form
is the summation of the absolute values of all the entries of M. W is the weighting matrix with each row having the form ![$$[w, 1, \ldots , 1]$$](/wp-content/uploads/2016/09/A339424_1_En_5_Chapter_IEq67.gif) where w is used to adjust the penalty for choosing the isotropic basis function in a voxel. The value of w can be obtained a-priori from a probabilistic segmentation of the T1-weighted image of the brain. Thus, w is small in the CSF and large in white and gray-matter areas.
where w is used to adjust the penalty for choosing the isotropic basis function in a voxel. The value of w can be obtained a-priori from a probabilistic segmentation of the T1-weighted image of the brain. Thus, w is small in the CSF and large in white and gray-matter areas.
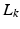 ,
, 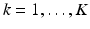 , denote the K low-resolution diffusion weighted imaging (DWI) volumes. For each
, denote the K low-resolution diffusion weighted imaging (DWI) volumes. For each 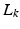 , the diffusion signal is acquired along a set of gradient directions
, the diffusion signal is acquired along a set of gradient directions 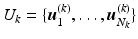 at the same b-value. The set of gradient directions for each LR image
at the same b-value. The set of gradient directions for each LR image 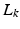 is assumed to be different, i.e.
is assumed to be different, i.e. 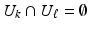 for
for 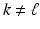 . The HR image that has
. The HR image that has 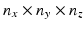 voxels and
voxels and 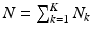 gradient directions is denoted by a matrix H of size
gradient directions is denoted by a matrix H of size 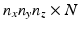 . Then, each LR image
. Then, each LR image 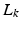 is given by
is given by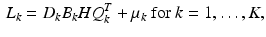
(3)
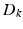 denotes the down-sampling matrix that averages neighboring slices,
denotes the down-sampling matrix that averages neighboring slices, 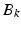 denotes the blurring (or point-spread function) and
denotes the blurring (or point-spread function) and 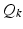 is the sub-sampling matrix in q-space. The main difference between the above model and the one used in [6, 15] is given by the
is the sub-sampling matrix in q-space. The main difference between the above model and the one used in [6, 15] is given by the 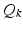 ’s that allow the LR images to have different sets of gradient directions. Further, we use the spherical ridgelets basis to model the diffusion signal at each voxel of H. To this end, H is assumed to satisfy
’s that allow the LR images to have different sets of gradient directions. Further, we use the spherical ridgelets basis to model the diffusion signal at each voxel of H. To this end, H is assumed to satisfy 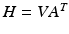 with A being the basis matrix of spherical ridgelets (SR) constructed along the set of gradient directions
with A being the basis matrix of spherical ridgelets (SR) constructed along the set of gradient directions 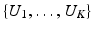 and each row vector of V being the SR coefficients at the corresponding voxel. Since each basis function is designed to model a diffusion signal with certain degree of anisotropy, a non-negative combination of spherical ridgelets provides more robust representation for diffusion signals especially when the SNR is low. Hence, the coefficients V are restricted to be non-negative. Following (1), we estimate H by solving
and each row vector of V being the SR coefficients at the corresponding voxel. Since each basis function is designed to model a diffusion signal with certain degree of anisotropy, a non-negative combination of spherical ridgelets provides more robust representation for diffusion signals especially when the SNR is low. Hence, the coefficients V are restricted to be non-negative. Following (1), we estimate H by solving
(4)
 denotes the element-wise multiplication,
denotes the element-wise multiplication,  is the squared Frobenius norm of a matrix M and
is the squared Frobenius norm of a matrix M and  is the summation of the absolute values of all the entries of M. W is the weighting matrix with each row having the form
is the summation of the absolute values of all the entries of M. W is the weighting matrix with each row having the form ![$$[w, 1, \ldots , 1]$$](/wp-content/uploads/2016/09/A339424_1_En_5_Chapter_IEq67.gif) where w is used to adjust the penalty for choosing the isotropic basis function in a voxel. The value of w can be obtained a-priori from a probabilistic segmentation of the T1-weighted image of the brain. Thus, w is small in the CSF and large in white and gray-matter areas.
where w is used to adjust the penalty for choosing the isotropic basis function in a voxel. The value of w can be obtained a-priori from a probabilistic segmentation of the T1-weighted image of the brain. Thus, w is small in the CSF and large in white and gray-matter areas.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree