1 Computer Language
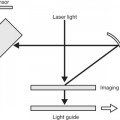
| Keyboard Each key represents a number of electrical signals (a stream of electrons and spaces) |
|
| To input data A key is depressed |
|
| For each key depressed A number of electrical impulses (signals and non-signals) are sent to the computer |
|
| Silicon chip The circuits on the silicon chips are activated |
|
| Signal A corresponding signal is sent to the screen (composed of signals and non-signals) |
|
| Image formation When an electron interacts with the screen the screen fluoresces When there are no electrons it does not fluoresce |
|
| Example image of a letter T | |
| 111111 | |
| 001100 | |
| 001100 Where 0 = no electron and 1 = electron | |
| 001100 | |
| Decimal System |
• To base 10
• Each column represents an increase by a factor of 10, e.g. ten (10), hundred (100), thousand (1000), etc.
• This system is too complex for computers to handle in this format
|
| Binary |
• To base 2
• Each column represents an increase by a factor of 2, e.g. two (2), four (4), eight (8), sixteen (16), thirty two (32), sixty four (64), etc.
|
| A 64 32 16 8 4 2 1 = Decimal numbers | |
| B 1 1 1 0 1 1 0 = Binary number | |
| C 0 1 0 1 0 0 1 = Binary number | |
| To Change Binary to Decimal (This can be done automatically by using a computer’s Scientific Calculator) |
Example 1 |
|
• Take row B above and read off the corresponding numbers in row A
• = 64, 32, 16, 4, 2
• Add the numbers together = 118
• Therefore 1110110 = 118
|
|
| Example 2 | |
|
• Take row C above and read off the corresponding numbers in row A
• 32, 8, 1
• Add the numbers together = 41
• Therefore 0101001 = 41
|
|
| To Change Decimal to Binary (This can be done automatically by using a computer’s Scientific Calculator) |
128 64 32 16 8 4 2 1 |
| Example | |
• 118 is smaller than 128 therefore = 0
• 118 is larger than 64 therefore = 1 (118 – 64 = 54)
• 54 is larger than 32 therefore = 1 (54 – 32 = 22)
• 22 is larger than 16 therefore = 1 (22 – 16 = 6)
• 6 is smaller than 8 therefore = 0
• 6 is larger than 4 therefore = 1 (6 – 4 = 2)
• 2 is the same as 2 therefore = 1 (2 – 2 = 0)
• 0 is smaller than 1 therefore = 0
Bit
(BInary digiT)
• The smallest piece of information that a computer can handle
• Represented by a simple electrical signal
• Which is either ON or OFF
• 0 represents OFF
• 1 represents ON
Byte
• Equals 8 bits
• Can represent numbers 0 to 255 inclusive
• Which is 256 different combinations of ON and OFF
• The main use for the numbers 0 to 255 is in the ASCII code (The American Standard Code for Information Exchange) to designate numbers, characters and symbols used on the computer keyboard
Example[Decimal] [Character] [Character]115 01110011 s34 00100010 ″68 01000100 DHexadecimal System
• To the base 16
• Using numbers 0 to 9 and letters A to F
• Therefore representing large (decimal or binary numbers) with fewer characters
• Conversion can be done automatically by using a computer’s Scientific Calculator up to a maximum of 16 digits using Qword option
Table 1.1 Comparison of decimal, hexadecimal and binary number systems 0–20
| Decimal | Hexadecimal | Binary |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | 11 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 |
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree