, which can be the input image or input template and subject images, the objective is to find a shape that matches the objects in the input image or a deformation field that matches the two images. Based on the MAP framework, such a problem can be described as maximizing the following posterior distribution [28]:
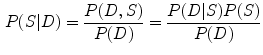
(1)
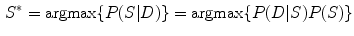
(2)
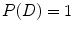 because the input data
because the input data 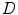 is known already.
is known already. 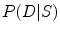 is the conditional probability of obtaining data
is the conditional probability of obtaining data 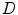 given the shape
given the shape 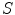 , and
, and 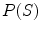 is the prior distribution of shape
is the prior distribution of shape 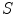 . So the solution of Eq. (2) is to find the best shape
. So the solution of Eq. (2) is to find the best shape 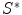 so that it not only gives higher probability of the observed data
so that it not only gives higher probability of the observed data 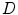 but also subject to a higher probability according to the prior distribution of the shape.
but also subject to a higher probability according to the prior distribution of the shape.When the probabilities are described by the Gibbs distribution [29, 30], the MAP problem is equivalent to minimizing the energy function:
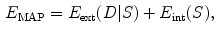
where 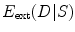 stands for the external energy term that reflects the matching degree between shape
stands for the external energy term that reflects the matching degree between shape 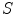 and the input image
and the input image 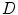 . One example in deformable shape matching is that the external energy term is defined as the matching degree between the shape (curve) and the object boundary features (such as boundaries) extracted from the image.
. One example in deformable shape matching is that the external energy term is defined as the matching degree between the shape (curve) and the object boundary features (such as boundaries) extracted from the image. 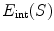 is the internal energy term that regularizes the shape itself. If the shapes from different subjects vary largely, normally the constraints are defined as the smoothness or topological regularizations. If the shapes from different subjects are similar but are subject to local elastic changes, a statistical shape model can be used to capture the variability of the shapes from a number of training samples, and then such a shape distribution can be used as the regularization term (internal energy) in Eq. (3). In many medical image computing tasks, because the shapes of organs are similar cross different subjects unless there exist some pathological conditions, statistical model-based methods play an important role in regularizing such shape variability. Therefore, many deformable model methods and statistical atlas based deformable registration algorithms fall in this MAP formulation. In deformable models, different internal and external energy/force terms are defined for automatic object matching.
is the internal energy term that regularizes the shape itself. If the shapes from different subjects vary largely, normally the constraints are defined as the smoothness or topological regularizations. If the shapes from different subjects are similar but are subject to local elastic changes, a statistical shape model can be used to capture the variability of the shapes from a number of training samples, and then such a shape distribution can be used as the regularization term (internal energy) in Eq. (3). In many medical image computing tasks, because the shapes of organs are similar cross different subjects unless there exist some pathological conditions, statistical model-based methods play an important role in regularizing such shape variability. Therefore, many deformable model methods and statistical atlas based deformable registration algorithms fall in this MAP formulation. In deformable models, different internal and external energy/force terms are defined for automatic object matching.
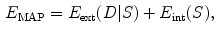
(3)
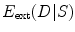 stands for the external energy term that reflects the matching degree between shape
stands for the external energy term that reflects the matching degree between shape 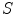 and the input image
and the input image 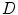 . One example in deformable shape matching is that the external energy term is defined as the matching degree between the shape (curve) and the object boundary features (such as boundaries) extracted from the image.
. One example in deformable shape matching is that the external energy term is defined as the matching degree between the shape (curve) and the object boundary features (such as boundaries) extracted from the image. 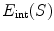 is the internal energy term that regularizes the shape itself. If the shapes from different subjects vary largely, normally the constraints are defined as the smoothness or topological regularizations. If the shapes from different subjects are similar but are subject to local elastic changes, a statistical shape model can be used to capture the variability of the shapes from a number of training samples, and then such a shape distribution can be used as the regularization term (internal energy) in Eq. (3). In many medical image computing tasks, because the shapes of organs are similar cross different subjects unless there exist some pathological conditions, statistical model-based methods play an important role in regularizing such shape variability. Therefore, many deformable model methods and statistical atlas based deformable registration algorithms fall in this MAP formulation. In deformable models, different internal and external energy/force terms are defined for automatic object matching.
is the internal energy term that regularizes the shape itself. If the shapes from different subjects vary largely, normally the constraints are defined as the smoothness or topological regularizations. If the shapes from different subjects are similar but are subject to local elastic changes, a statistical shape model can be used to capture the variability of the shapes from a number of training samples, and then such a shape distribution can be used as the regularization term (internal energy) in Eq. (3). In many medical image computing tasks, because the shapes of organs are similar cross different subjects unless there exist some pathological conditions, statistical model-based methods play an important role in regularizing such shape variability. Therefore, many deformable model methods and statistical atlas based deformable registration algorithms fall in this MAP formulation. In deformable models, different internal and external energy/force terms are defined for automatic object matching.In image registration, we can use different notes to describe the MAP method, but the formulation remains the same. Given two images, the template 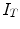 and the subject
and the subject 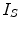 , the goal is to find the deformation field that aligns the two images. According to MAP, the goal is to find that
, the goal is to find the deformation field that aligns the two images. According to MAP, the goal is to find that 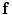 maximizes the following posterior distribution:
maximizes the following posterior distribution:
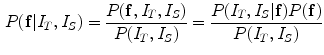
Similarly, using the Gibbs distribution, the MAP problem is equivalent to minimizing the energy function:
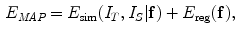
where 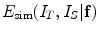 stands for the image distance measure (the reverse of image similarity measure) between the two images under the current deformation field
stands for the image distance measure (the reverse of image similarity measure) between the two images under the current deformation field 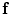 .
. 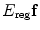 is the regularization term of the deformation field.
is the regularization term of the deformation field.
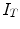 and the subject
and the subject 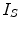 , the goal is to find the deformation field that aligns the two images. According to MAP, the goal is to find that
, the goal is to find the deformation field that aligns the two images. According to MAP, the goal is to find that 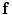 maximizes the following posterior distribution:
maximizes the following posterior distribution: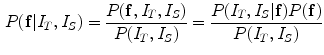
(4)
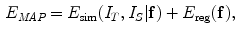
(5)
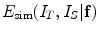 stands for the image distance measure (the reverse of image similarity measure) between the two images under the current deformation field
stands for the image distance measure (the reverse of image similarity measure) between the two images under the current deformation field 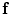 .
. 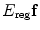 is the regularization term of the deformation field.
is the regularization term of the deformation field.Comparing Eqs. (3) and (5), we can see that they are actually the same kind of formulation, and we use different names for the sake of different conventions in segmentation and registration. The difference is that now in image registration, the image similarity energy term calculates the differences between the two images, such as the sum of voxel-wise intensity differences or mutual information of the subject image and the deformed template image using f. Similar to the internal energy, the deformation field regularization term here can use either smoothness and topological regularization or can be derived from a statistical model if the template image is fixed, and multiple images need to be registered onto the same template.
3 The Bayesian Model (BM) Framework
One drawback of the MAP is that it might over regularize the shapes during the matching procedure. The reason is that from the formulation we can see that the final result must be exactly subject to the prior distribution. In another word, the MAP method requires that the resultant shape is subject to the prior distribution. This renders that it may not be able to match a new image accurately if the variations of the shape are not presented in the sample data. For example, if a PCA model is used, because of the limited numbers of principal components used, the shape reconstructed from PCA model cannot reflect the detailed variability of the high-dimensional data.
It is in this context that we proposed a Bayesian shape model (BSM), which is also referred to as Bayesian model (BM) in this chapter. In BM, an intermediate shape is introduced in the matching procedure. In this section, the BM is first presented in the context of shape-based segmentation, and then, its application to image registration is introduced.
Given the input image or data 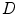 , our goal is to jointly estimate the resultant shape
, our goal is to jointly estimate the resultant shape 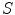 and an intermediate shape
and an intermediate shape 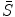 by maximizing the following posterior probability [27, 31]:
by maximizing the following posterior probability [27, 31]:
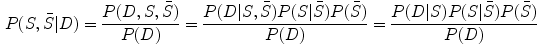
It can be seen that by using an intermediate shape 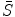 , we can decouple the two requirements in the matching procedure. Namely, we require that the resultant shape
, we can decouple the two requirements in the matching procedure. Namely, we require that the resultant shape 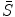 match the image data and the intermediate shape match the requirement of prior distribution. So these two shapes do not need to be the same as in the ASM model. The middle term requires that the two shapes are close with each other. This is the advantage of BM, and on one hand, the prior shape constraint is applied and on the other hand, the formulation allows for flexibility to better match the object.
match the image data and the intermediate shape match the requirement of prior distribution. So these two shapes do not need to be the same as in the ASM model. The middle term requires that the two shapes are close with each other. This is the advantage of BM, and on one hand, the prior shape constraint is applied and on the other hand, the formulation allows for flexibility to better match the object.
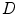 , our goal is to jointly estimate the resultant shape
, our goal is to jointly estimate the resultant shape 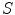 and an intermediate shape
and an intermediate shape 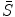 by maximizing the following posterior probability [27, 31]:
by maximizing the following posterior probability [27, 31]: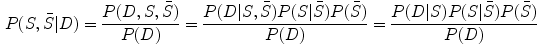
(6)
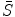 , we can decouple the two requirements in the matching procedure. Namely, we require that the resultant shape
, we can decouple the two requirements in the matching procedure. Namely, we require that the resultant shape 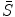 match the image data and the intermediate shape match the requirement of prior distribution. So these two shapes do not need to be the same as in the ASM model. The middle term requires that the two shapes are close with each other. This is the advantage of BM, and on one hand, the prior shape constraint is applied and on the other hand, the formulation allows for flexibility to better match the object.
match the image data and the intermediate shape match the requirement of prior distribution. So these two shapes do not need to be the same as in the ASM model. The middle term requires that the two shapes are close with each other. This is the advantage of BM, and on one hand, the prior shape constraint is applied and on the other hand, the formulation allows for flexibility to better match the object.The final derivation in Eq. (6) is based on the assumption that the data 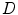 and the intermediate shape
and the intermediate shape 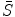 are independent each other. This may not be exactly true but in practice if we are not requiring a match between the intermediate shape
are independent each other. This may not be exactly true but in practice if we are not requiring a match between the intermediate shape 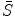 and the input data
and the input data 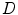 , it is a valid assumption in the formulation. Using the Gibbs distribution, the problem is equivalent to minimizing the energy function:
, it is a valid assumption in the formulation. Using the Gibbs distribution, the problem is equivalent to minimizing the energy function:
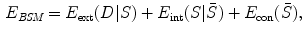
where 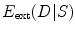 stands for the external energy that matches the shape S with the image
stands for the external energy that matches the shape S with the image 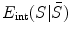 , represents the distance between the two shapes, and
, represents the distance between the two shapes, and 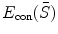 is the constraint energy term that regularizes the intermediate shape
is the constraint energy term that regularizes the intermediate shape 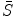 . We can use the smoothness constraints or statistical model constraints to define
. We can use the smoothness constraints or statistical model constraints to define 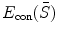 .
.
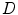 and the intermediate shape
and the intermediate shape 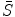 are independent each other. This may not be exactly true but in practice if we are not requiring a match between the intermediate shape
are independent each other. This may not be exactly true but in practice if we are not requiring a match between the intermediate shape 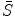 and the input data
and the input data 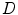 , it is a valid assumption in the formulation. Using the Gibbs distribution, the problem is equivalent to minimizing the energy function:
, it is a valid assumption in the formulation. Using the Gibbs distribution, the problem is equivalent to minimizing the energy function: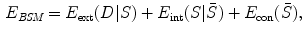
(7)
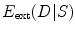 stands for the external energy that matches the shape S with the image
stands for the external energy that matches the shape S with the image 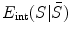 , represents the distance between the two shapes, and
, represents the distance between the two shapes, and 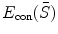 is the constraint energy term that regularizes the intermediate shape
is the constraint energy term that regularizes the intermediate shape 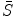 . We can use the smoothness constraints or statistical model constraints to define
. We can use the smoothness constraints or statistical model constraints to define 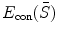 .
.The key feature for BM is that now we are solving a shape S that on one hand matches the image data 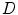 , and on the other hand, to be as close as the intermediate shape
, and on the other hand, to be as close as the intermediate shape 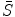 , which is regularized by the constraint energy term. In this way, the resultant shape
, which is regularized by the constraint energy term. In this way, the resultant shape 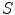 is not necessarily the exact regularized shape according to the shape priors. Such a formulation allows for accurate matching of the object shape, while still be regularized by the prior information.
is not necessarily the exact regularized shape according to the shape priors. Such a formulation allows for accurate matching of the object shape, while still be regularized by the prior information.
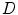 , and on the other hand, to be as close as the intermediate shape
, and on the other hand, to be as close as the intermediate shape 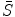 , which is regularized by the constraint energy term. In this way, the resultant shape
, which is regularized by the constraint energy term. In this way, the resultant shape 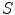 is not necessarily the exact regularized shape according to the shape priors. Such a formulation allows for accurate matching of the object shape, while still be regularized by the prior information.
is not necessarily the exact regularized shape according to the shape priors. Such a formulation allows for accurate matching of the object shape, while still be regularized by the prior information.We now translate the BM into image registration applications. According to the BM framework, the goal of image registration is to solve jointly the deformation field f and an intermediate deformation 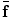 field by maximizing the following posterior distribution [27]:
field by maximizing the following posterior distribution [27]:
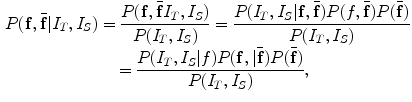
Similarly, using the Gibbs distribution, the BM problem is equivalent to minimizing the energy function:
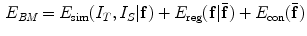
where 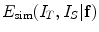 stands for the image similarity measure,
stands for the image similarity measure, 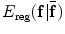 is the regularization of
is the regularization of 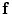 , and
, and 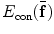 is the constraint energy of the deformation field.
is the constraint energy of the deformation field. 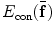 can be modeled using statistical models of the training deformations defined on the same template image space.
can be modeled using statistical models of the training deformations defined on the same template image space.
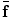 field by maximizing the following posterior distribution [27]:
field by maximizing the following posterior distribution [27]: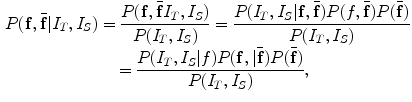
(8)
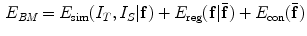
(9)
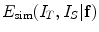 stands for the image similarity measure,
stands for the image similarity measure, 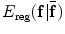 is the regularization of
is the regularization of 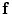 , and
, and 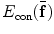 is the constraint energy of the deformation field.
is the constraint energy of the deformation field. 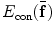 can be modeled using statistical models of the training deformations defined on the same template image space.
can be modeled using statistical models of the training deformations defined on the same template image space.In fact, by comparing Eq. (5) with (9), we can see that the use of intermediate deformation 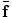 in the BM method relaxes the direct regularization of the deformation field and increases its flexibility. This formulation allows for more accurate registration of medical images. If no statistical models are used, e.g., only using smoothness constraints, such an intermediate matching procedure may not be necessary and the MAP method may perform similar to the BM. Because for high dimensional shape and deformation data, the generalization and specificity of statistical models may be limited, requiring the result to be exactly subject to the prior distribution could be loosed by using the BM method.
in the BM method relaxes the direct regularization of the deformation field and increases its flexibility. This formulation allows for more accurate registration of medical images. If no statistical models are used, e.g., only using smoothness constraints, such an intermediate matching procedure may not be necessary and the MAP method may perform similar to the BM. Because for high dimensional shape and deformation data, the generalization and specificity of statistical models may be limited, requiring the result to be exactly subject to the prior distribution could be loosed by using the BM method.
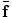 in the BM method relaxes the direct regularization of the deformation field and increases its flexibility. This formulation allows for more accurate registration of medical images. If no statistical models are used, e.g., only using smoothness constraints, such an intermediate matching procedure may not be necessary and the MAP method may perform similar to the BM. Because for high dimensional shape and deformation data, the generalization and specificity of statistical models may be limited, requiring the result to be exactly subject to the prior distribution could be loosed by using the BM method.
in the BM method relaxes the direct regularization of the deformation field and increases its flexibility. This formulation allows for more accurate registration of medical images. If no statistical models are used, e.g., only using smoothness constraints, such an intermediate matching procedure may not be necessary and the MAP method may perform similar to the BM. Because for high dimensional shape and deformation data, the generalization and specificity of statistical models may be limited, requiring the result to be exactly subject to the prior distribution could be loosed by using the BM method.In the next two sections, we introduce the applications of the BM framework in medical image segmentation and registration. First, in Sect. 4, we introduce an atlas-based level-set segmentation for MR brain images, where the BM framework has been applied to use the statistical models of level-set functions in the atlas space for constraining the segmentation of anatomical structures in subject images. This comes up with a new joint parametric and nonparametric segmentation [32, 33]. Then, in Sect. 5, we introduce a statistical model of deformation (SMD) constrained image registration algorithm [19, 34]. Although with different applications, both algorithms apply the same basic methodology presented in this Section.
4 BM for Medical Image Segmentation
4.1 Introduction
In this chapter we introduce how to apply BM in level-set-based MR brain image segmentation. Image segmentation or automatic extraction of anatomical structures plays an important role in medical image analysis. In the literature, various deformable models or partial differential equation (PDE)-based methods have been proposed to extract the anatomical structures of interest in medical images. These model scan also be regarded as model fitting problems in a probabilistic framework [7] based on the Bayes’ theorem, where the input image is divided into different regions by matching the external and internal hidden features so that the posteriori probability of the segmentation is maximized.
The internal features reflect the geometric properties of the evolving curve such as curvature, curve-length, and smoothness measures. They are represented by either explicit or implicit curved descriptors. An unjustified property of explicit descriptors is that geometrical evolution of a curve is not intrinsic since it is dependent on the way the curve is parameterized. Implicit curve descriptors are generally parameterized by arc-length [33, 35, 36]. One of the typical methods using implicit curve descriptor, known as the level set method [37], has become very important in image segmentation due to its advantages such as parameter-free representation of curves and easy handling of topology changes.
The external features are traditionally represented by image specific information such as image gradient [2, 33, 35, 36, 38], or regional information [3, 39]. Particularly, in boundary-based approaches with an implicit curve representation [33, 36] curve evolution is achieved by defining a geodesic curve of minimal weighted length and a boundary-based metric from image data. However, these methods are sensitive to noise or images with poor contrast, and they often stuck in local minima since the objective functions rely on boundary-based external features and there is no global shape constraints about the object shape to be matched.
On the other hand, region-based external features are defined as regional image statistics inside and outside the contours and are more stable than boundary-based features. Mumford and Shah [40] proposed a new energy function in the variation framework. The aim is to find smooth regions as optimal piecewise approximation of input image and with sharp boundaries by minimizing the energy function. In order to simplify the optimization process, Mumford and Shah’s energy function is used in greedy algorithm based on the region growing and merging [41] or in statistical framework [39].
Another solution was proposed by Chan and Vese [3] to provide an efficient variation formulation in level set representation for minimizing the Mumford–Shah energy function [42–44]. In curve evolution-based methods, regional image statistics are obtained based on the parametric statistics [39, 43, 44]. However,the performance of parametric methods can be depended on the assumed parametric models and the class of input images. Therefore,nonparametric methods such as Parzen windowing are used to estimate the underlying distribution of the pixel intensities within each region [23, 41, 45]. Another way to improve region-based methods is to integrate prior knowledge into image-based segmentation function to process globally high-level information of object shapes. This knowledge is trained as the object-oriented model based on using learning procedures, for example on space of implicit function [4, 46–48], Fourier-driven curve representation [8, 33], and parametric space of curve representation [11, 12, 15].
One important property of the model-based approach is that the variability of object shapes is captured from training samples and acts as the shape priors. According to level set representation,the shape prior information can be used on both linear subspace of parametric level set function spanned by principal components and nonlinear space of nonparametric level set function. In parametric curve evolution on linear subspace, Tsai et al. [5] proposed to parameterize the level set energy function with respect to shape and pose parameters. Curve evolution is performed parametrically via updating the shape and poses parameters constrained by the statistical parametric model obtained using Principal Component Analysis (PCA). In nonlinear space of evolving curve, Leventon et al. [49] used PCA directly on the space of implicit functions to estimate principal modes of shape variation of training samples. This prior information constraints and regularizes the evolving curve derived separately by image specific energy term in [36]. In order to couple segmentation and prior model, Rousson [48] proposed a statistical prior model in variational form and included an average shape and mode of variation defined from training samples. This statistical model is integrated with an existing data-driven variational method to extract the objects. One can instead estimate and impose the shape prior information on the zero-crossing rather than on the level set function using variational framework. For promising extensions, based on the level set representation in statistical shape prior models, Charpiat et al. [50] proposed nonlinear shape metrics and estimated the principal shape variations.
Cremers et al. [51] proposed nonlinear statistical shape model by performing kernel PCA along level set-based Mumford–Shah segmentation [40]. In [52] and [4], nonparametric density estimation forshape priors is assimilated in the level set framework to extract object. In summary, the parametric statistical model-based curve evolution enforces the constraints about the underlying shapes by the shape prior and therefore the algorithm is robust and less affected by noise or low image contrast. On the other hand, the nonparametric evolution energy term can handle infinite degree of curve variations and helps us to achieve better accuracy than the method that only uses the parametric statistical models.
Recent works by [53] and [46] also use similar statistical model in level set method. These approaches directly apply a PCA model to constrain the level set function while matching it with the image features. Thus, the level set function is more constrained by the prior distribution. The optimization procedure of the curve is achieved using the calculus of variation on the nonlinear space of nonparametric level set function.
As described in the previous section, BM facilitates a joint estimation of the resultant shape and an intermediate shape simultaneously. Thus, we can integrate the advantageous of both parametric and nonparametric curve evolution using in the BM framework. The core of such joint curve evolution is a unified energy function that drives the active contour toward the desired boundaries through two steps. In the first step, the curve is driven by the nonparametric level set function toward a homogeneous intensity regions and constraint by the parametric shape-based model. Therefore, minimization process of this step is achieved on nonlinear space of level set function. In the second step, the curve is optimized by parametric level set function and is driven toward the global shape prior and image regions parametrically and constraint by nonparametric model from previous step. Optimization of the second step is achieved on linear subspace spanned by principal components obtained in statistical shape-based model. Therefore,in the joint curve evolution, both local features such as statistical region properties of the image, curvature and length of the curve and global features of the object such as shape and position parameters are updating respectively through these two steps. In this way, two curves are used to match the object shape in an iterative manner. They are jointly constrained via a similarity measure between them in each iterative evolution. Finally, the nonparametric level set curve is regarded as the final matching result since it is more accurate as compared to the parametric curve.
In experiments, the proposed algorithm has been applied to segment the frontal horns of ventricles and putamen of MR brain images. The reason that we choose these two structures is that the boundaries of the ventricle frontal horn are very clear, while the white matter/gray matter contrast of putamen boundaries is lower compared to other anatomical structures of the brain. Thus we can fully evaluate the performance of the algorithm under different conditions. The comparative results have shown that the proposed joint curve evolution is as robust as Tsai et al. method and yields more accurate results as compared with the parametric only statistical model [5] and nonparametric model [3] by using manually marked curves as the gold standard.
4.2 Previous Methods
Before introducing the joint BM segmentation method, we briefly introduce the nonparametric and parametric curve evolution algorithms that the joint curve evolution algorithm is built on.
Nonparametric Curve Evolution
Chan and Vese proposed a nonparametric curve evolution method by solving the Mumford Shah problem, called minimum partition [3]. From the variational analysis point of view, the basic idea of the algorithm is to find the level set function 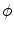 a given image
a given image 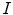 by minimizing the energy function,
by minimizing the energy function,
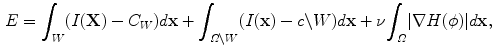
where 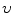 is a constant. The shape
is a constant. The shape 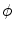 divides the image domain
divides the image domain 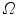 into two homogeneous regions W and
into two homogeneous regions W and 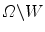 . W represents object region and
. W represents object region and 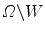 is the region outside the object.
is the region outside the object. 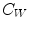 is the average intensity of image within region W , and
is the average intensity of image within region W , and 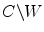 is the average intensity within region
is the average intensity within region 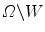 .
. 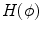 is the level set function and
is the level set function and 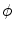 is the shape represented by the zero level set. It can be seen that this nonparametric curve evolution algorithm uses region-based image features and infinite degree of curve variation for image segmentation.
is the shape represented by the zero level set. It can be seen that this nonparametric curve evolution algorithm uses region-based image features and infinite degree of curve variation for image segmentation.
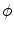 a given image
a given image 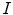 by minimizing the energy function,
by minimizing the energy function,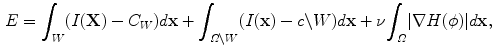
(10)
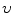 is a constant. The shape
is a constant. The shape 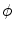 divides the image domain
divides the image domain 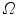 into two homogeneous regions W and
into two homogeneous regions W and 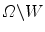 . W represents object region and
. W represents object region and 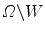 is the region outside the object.
is the region outside the object. 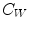 is the average intensity of image within region W , and
is the average intensity of image within region W , and 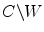 is the average intensity within region
is the average intensity within region 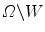 .
. 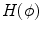 is the level set function and
is the level set function and 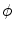 is the shape represented by the zero level set. It can be seen that this nonparametric curve evolution algorithm uses region-based image features and infinite degree of curve variation for image segmentation.
is the shape represented by the zero level set. It can be seen that this nonparametric curve evolution algorithm uses region-based image features and infinite degree of curve variation for image segmentation.Parametric Model-Based Curve Evolution
In order to improve robustness, many statistical model-based methods have been proposed to constrain the evolution of level set functions. Tsai et al. [5] integrated parametric statistical shape modeling with the region-based curve evolution to drive the curve by using the statistical shape model as constraints. The shape variability is estimated by performing PCA on the globally aligned level set functions, and the major shape variation is then statistically reflected by the changes along the principal components. Subsequently, a parametric level set function 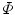 can be described as a function of the feature vector in the PCA space, w, and the pose parameter p, reflecting a global transformation from the shape space onto the image space (see Eq. (12) for details). Then, the associated energy functions (similar to Eq. (10)) can be defined as follows,
can be described as a function of the feature vector in the PCA space, w, and the pose parameter p, reflecting a global transformation from the shape space onto the image space (see Eq. (12) for details). Then, the associated energy functions (similar to Eq. (10)) can be defined as follows,
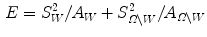
Notice that the parametric level set function 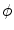 is determined by w and p, and it divides the image domain into two regions: inside
is determined by w and p, and it divides the image domain into two regions: inside 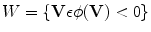 and outside
and outside 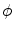 , the areas of these two regions are
, the areas of these two regions are 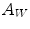 and
and 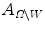 , and
, and 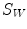 and
and 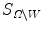 are the total intensities of these regions.
are the total intensities of these regions.
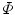 can be described as a function of the feature vector in the PCA space, w, and the pose parameter p, reflecting a global transformation from the shape space onto the image space (see Eq. (12) for details). Then, the associated energy functions (similar to Eq. (10)) can be defined as follows,
can be described as a function of the feature vector in the PCA space, w, and the pose parameter p, reflecting a global transformation from the shape space onto the image space (see Eq. (12) for details). Then, the associated energy functions (similar to Eq. (10)) can be defined as follows,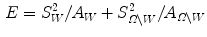
(11)
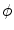 is determined by w and p, and it divides the image domain into two regions: inside
is determined by w and p, and it divides the image domain into two regions: inside 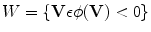 and outside
and outside 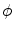 , the areas of these two regions are
, the areas of these two regions are 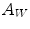 and
and 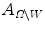 , and
, and 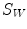 and
and 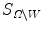 are the total intensities of these regions.
are the total intensities of these regions.Notice that the energy functions in Eqs. (10) and (11) are similar, but the difference is that the zero level set curve in nonparametric curve evolution means the shape 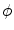 is defined by a free-form level set, while in parametric-model based curve evolution, the shape is defined by a parametric model
is defined by a free-form level set, while in parametric-model based curve evolution, the shape is defined by a parametric model ![$$\varPhi [\mathbf{W,P}]$$](/wp-content/uploads/2016/10/A312883_1_En_4_Chapter_IEq67.gif) , and will be detailed in the following section.
, and will be detailed in the following section.
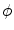 is defined by a free-form level set, while in parametric-model based curve evolution, the shape is defined by a parametric model
is defined by a free-form level set, while in parametric-model based curve evolution, the shape is defined by a parametric model ![$$\varPhi [\mathbf{W,P}]$$](/wp-content/uploads/2016/10/A312883_1_En_4_Chapter_IEq67.gif) , and will be detailed in the following section.
, and will be detailed in the following section.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree