-weighted images from 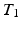 -weighted images, showing improved synthesis quality as compared to current image synthesis approaches. We also synthesized Fluid Attenuated Inversion Recovery (FLAIR) images, showing similar segmentations to those obtained from real FLAIRs. Additionally, we generated super-resolution FLAIRs showing improved segmentation.
-weighted images, showing improved synthesis quality as compared to current image synthesis approaches. We also synthesized Fluid Attenuated Inversion Recovery (FLAIR) images, showing similar segmentations to those obtained from real FLAIRs. Additionally, we generated super-resolution FLAIRs showing improved segmentation.
Keywords
Magnetic resonanceImage synthesisConditional random field1 Introduction
Image synthesis in MRI is a process in which the intensities of acquired MRI data are transformed in order to enhance the data quality or render them more suitable as input for further image processing. Image synthesis has been gaining traction in the medical image processing community in recent years [6, 15], as a useful pre-processing tool for segmentation and registration. It is especially useful in MR brain imaging, where a staggering variety of pulse sequences like Magnetization Prepared Gradient Echo (MPRAGE), Dual Spin Echo (DSE), FLAIR etc. are used to interrogate the various aspects of neuroanatomy. Versatility of MRI is a boon for diagnosticians but can sometimes prove to be a handicap when performing analysis using image processing. Automated image processing algorithms are not always robust to variations in their input [13]. In large datasets, sometimes images are missing or corrupted during acquisition and cannot be used for further processing. Image synthesis can be used as a tool to supplement these datasets by creating artificial facsimiles of the missing images by using the available ones. An additional source of variability is the differing image quality between different pulse sequences for the same subject. An MPRAGE sequence can be quickly acquired at a resolution higher than 1 mm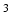 , which is not possible for FLAIR. Image synthesis can be used to enhance the resolution of existing low resolution FLAIRs using the corresponding high resolution MPRAGE images, thus leading to improved tissue segmentation.
, which is not possible for FLAIR. Image synthesis can be used to enhance the resolution of existing low resolution FLAIRs using the corresponding high resolution MPRAGE images, thus leading to improved tissue segmentation.
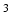 , which is not possible for FLAIR. Image synthesis can be used to enhance the resolution of existing low resolution FLAIRs using the corresponding high resolution MPRAGE images, thus leading to improved tissue segmentation.
, which is not possible for FLAIR. Image synthesis can be used to enhance the resolution of existing low resolution FLAIRs using the corresponding high resolution MPRAGE images, thus leading to improved tissue segmentation.Previous work on image synthesis has proceeded along two lines, (1) registration-based, and (2) example-based. Registration-based [3, 12] approaches register the training/atlas images to the given subject image and perform intensity fusion (in the case of multiple training/atlas pairs) to produce the final synthesis. These approaches are heavily dependent on the quality of registration, which is generally not accurate enough in the cortex and abnormal tissue regions. Example-based approaches involve learning an intensity transformation from known training data pairs/atlas images. A variety of example-based approaches [5, 8, 15] have been proposed. These methods treat the problem as a regression problem and estimate the synthetic image voxel-by-voxel from the given, available images. The voxel intensities in the synthetic image are assumed to be independent of each other, which is not entirely valid as intensities in a typical MR image are spatially correlated and vary smoothly from voxel-to-voxel.
In this work, we frame image synthesis as an inference problem in a probabilistic discriminative framework. Specifically, we model the posterior distribution 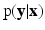 , where
, where 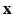 is the collection of known images and
is the collection of known images and 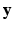 is the synthetic image we want to estimate, as a Gaussian CRF [10]. Markov random field (MRF) approaches lend themselves as a robust, popular way to model images. However in a typical MRF, the observed data
is the synthetic image we want to estimate, as a Gaussian CRF [10]. Markov random field (MRF) approaches lend themselves as a robust, popular way to model images. However in a typical MRF, the observed data 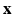 are assumed to be independent given the underlying latent variable
are assumed to be independent given the underlying latent variable 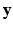 , which is a limiting assumption for typical images. A CRF, by directly modeling the posterior distribution allows us to side-step this problem. CRFs have been used in discrete labeling and segmentation problems [9]. A continuous-valued CRF, modeled as a Gaussian CRF, was first described in [17]. Efficient parameter learning and inference procedures of a Gaussian CRF were explored in the Regression Tree Fields concept in [7]. We also model the posterior distribution as a Gaussian CRF, the parameters of which are stored in the leaves of a single regression tree. We learn these parameters by maximizing a pseudo-likelihood objective function given training data. Given a subject image, we build the Gaussian distribution parameters from the learned tree and parameters. The prediction of the synthetic subject image is a maximum a posteriori (MAP) estimate of this distribution and is estimated efficiently using conjugate gradient descent.
, which is a limiting assumption for typical images. A CRF, by directly modeling the posterior distribution allows us to side-step this problem. CRFs have been used in discrete labeling and segmentation problems [9]. A continuous-valued CRF, modeled as a Gaussian CRF, was first described in [17]. Efficient parameter learning and inference procedures of a Gaussian CRF were explored in the Regression Tree Fields concept in [7]. We also model the posterior distribution as a Gaussian CRF, the parameters of which are stored in the leaves of a single regression tree. We learn these parameters by maximizing a pseudo-likelihood objective function given training data. Given a subject image, we build the Gaussian distribution parameters from the learned tree and parameters. The prediction of the synthetic subject image is a maximum a posteriori (MAP) estimate of this distribution and is estimated efficiently using conjugate gradient descent.
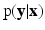 , where
, where 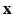 is the collection of known images and
is the collection of known images and 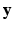 is the synthetic image we want to estimate, as a Gaussian CRF [10]. Markov random field (MRF) approaches lend themselves as a robust, popular way to model images. However in a typical MRF, the observed data
is the synthetic image we want to estimate, as a Gaussian CRF [10]. Markov random field (MRF) approaches lend themselves as a robust, popular way to model images. However in a typical MRF, the observed data 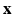 are assumed to be independent given the underlying latent variable
are assumed to be independent given the underlying latent variable 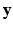 , which is a limiting assumption for typical images. A CRF, by directly modeling the posterior distribution allows us to side-step this problem. CRFs have been used in discrete labeling and segmentation problems [9]. A continuous-valued CRF, modeled as a Gaussian CRF, was first described in [17]. Efficient parameter learning and inference procedures of a Gaussian CRF were explored in the Regression Tree Fields concept in [7]. We also model the posterior distribution as a Gaussian CRF, the parameters of which are stored in the leaves of a single regression tree. We learn these parameters by maximizing a pseudo-likelihood objective function given training data. Given a subject image, we build the Gaussian distribution parameters from the learned tree and parameters. The prediction of the synthetic subject image is a maximum a posteriori (MAP) estimate of this distribution and is estimated efficiently using conjugate gradient descent.
, which is a limiting assumption for typical images. A CRF, by directly modeling the posterior distribution allows us to side-step this problem. CRFs have been used in discrete labeling and segmentation problems [9]. A continuous-valued CRF, modeled as a Gaussian CRF, was first described in [17]. Efficient parameter learning and inference procedures of a Gaussian CRF were explored in the Regression Tree Fields concept in [7]. We also model the posterior distribution as a Gaussian CRF, the parameters of which are stored in the leaves of a single regression tree. We learn these parameters by maximizing a pseudo-likelihood objective function given training data. Given a subject image, we build the Gaussian distribution parameters from the learned tree and parameters. The prediction of the synthetic subject image is a maximum a posteriori (MAP) estimate of this distribution and is estimated efficiently using conjugate gradient descent.We refer to our method as Synthesis with Conditional Random Field Tree or SyCRAFT. We applied SyCRAFT to synthesize 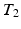 -weighted (
-weighted (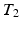 -w) images from
-w) images from 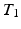 -w (
-w (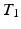 -w) images and showed a superior quality of synthesis compared to state-of-the-art methods. We also applied our method to synthesize FLAIRs from corresponding
-w) images and showed a superior quality of synthesis compared to state-of-the-art methods. We also applied our method to synthesize FLAIRs from corresponding 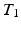 -w,
-w, 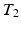 -w, and
-w, and 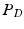 -weighted (
-weighted (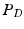 -w) images and showed that tissue segmentation on synthetic images is comparable to that achieved using real images. Finally, we used our method in an example-based super-resolution framework to estimate a super-resolution FLAIR image and showed improved tissue segmentation. In Sect. 2, we describe our method in detail, followed by experiments and results in Sect. 3 and discussion in Sect. 4.
-w) images and showed that tissue segmentation on synthetic images is comparable to that achieved using real images. Finally, we used our method in an example-based super-resolution framework to estimate a super-resolution FLAIR image and showed improved tissue segmentation. In Sect. 2, we describe our method in detail, followed by experiments and results in Sect. 3 and discussion in Sect. 4.
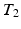 -weighted (
-weighted (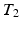 -w) images from
-w) images from 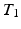 -w (
-w (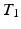 -w) images and showed a superior quality of synthesis compared to state-of-the-art methods. We also applied our method to synthesize FLAIRs from corresponding
-w) images and showed a superior quality of synthesis compared to state-of-the-art methods. We also applied our method to synthesize FLAIRs from corresponding 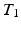 -w,
-w, 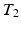 -w, and
-w, and 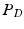 -weighted (
-weighted (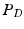 -w) images and showed that tissue segmentation on synthetic images is comparable to that achieved using real images. Finally, we used our method in an example-based super-resolution framework to estimate a super-resolution FLAIR image and showed improved tissue segmentation. In Sect. 2, we describe our method in detail, followed by experiments and results in Sect. 3 and discussion in Sect. 4.
-w) images and showed that tissue segmentation on synthetic images is comparable to that achieved using real images. Finally, we used our method in an example-based super-resolution framework to estimate a super-resolution FLAIR image and showed improved tissue segmentation. In Sect. 2, we describe our method in detail, followed by experiments and results in Sect. 3 and discussion in Sect. 4.2 Method
2.1 Model
We start with the definition of a CRF, initially proposed in [10]. A CRF is defined over a graph 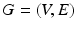 , V and E are the sets of vertices and edges respectively, of G. In an image synthesis context, the set of all voxels i in the image domain form the vertices of V. A pair of voxels
, V and E are the sets of vertices and edges respectively, of G. In an image synthesis context, the set of all voxels i in the image domain form the vertices of V. A pair of voxels 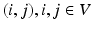 , that are neighbors according to a predefined neighborhood, form an edge in E. Let
, that are neighbors according to a predefined neighborhood, form an edge in E. Let 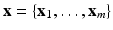 be the observed data. Specifically,
be the observed data. Specifically, 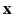 represents the collection of available images from m pulse sequences from which we want to synthesize a new image. Let
represents the collection of available images from m pulse sequences from which we want to synthesize a new image. Let 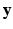 be the continuous-valued random variable over V, representing the synthetic image we want to predict. In a CRF framework,
be the continuous-valued random variable over V, representing the synthetic image we want to predict. In a CRF framework, 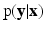 is modeled and learned from training data of known pairs of
is modeled and learned from training data of known pairs of 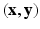 . Let
. Let 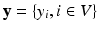 . Then
. Then 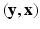 is a CRF if, conditioned on
is a CRF if, conditioned on 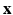 ,
, 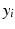 exhibit the Markov property, i.e.
exhibit the Markov property, i.e. 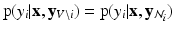 , where
, where 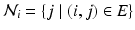 , is the neighborhood of i.
, is the neighborhood of i.
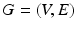 , V and E are the sets of vertices and edges respectively, of G. In an image synthesis context, the set of all voxels i in the image domain form the vertices of V. A pair of voxels
, V and E are the sets of vertices and edges respectively, of G. In an image synthesis context, the set of all voxels i in the image domain form the vertices of V. A pair of voxels 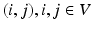 , that are neighbors according to a predefined neighborhood, form an edge in E. Let
, that are neighbors according to a predefined neighborhood, form an edge in E. Let 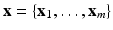 be the observed data. Specifically,
be the observed data. Specifically, 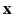 represents the collection of available images from m pulse sequences from which we want to synthesize a new image. Let
represents the collection of available images from m pulse sequences from which we want to synthesize a new image. Let 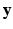 be the continuous-valued random variable over V, representing the synthetic image we want to predict. In a CRF framework,
be the continuous-valued random variable over V, representing the synthetic image we want to predict. In a CRF framework, 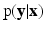 is modeled and learned from training data of known pairs of
is modeled and learned from training data of known pairs of 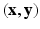 . Let
. Let 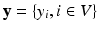 . Then
. Then 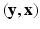 is a CRF if, conditioned on
is a CRF if, conditioned on 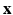 ,
, 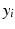 exhibit the Markov property, i.e.
exhibit the Markov property, i.e. 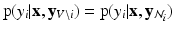 , where
, where 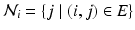 , is the neighborhood of i.
, is the neighborhood of i.Assuming 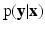 in terms of association potentials and interaction potentials is given as,
in terms of association potentials and interaction potentials is given as,
![$$\begin{aligned} \mathrm {p}(\mathbf{y}| \mathbf{x}) = \frac{1}{Z}\exp [-\{\sum _{i\in V} E_{\mathcal {A}}(y_i, \mathbf{x}; \theta ) + \lambda \sum _{i \in V} \sum _{j \in \mathcal {N}_i} E_{\mathcal {I}}(y_i, y_j,\mathbf{x};\theta )\}]. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_58_Chapter_Equ1.gif)
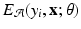 is called an association potential, defined using the parameter set
is called an association potential, defined using the parameter set 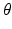 ,
, 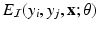 is called an interaction potential,
is called an interaction potential, 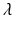 is a weighting factor, and Z is the partition function. If
is a weighting factor, and Z is the partition function. If 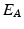 and
and 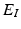 are defined as quadratic functions of
are defined as quadratic functions of 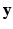 , we can express this distribution as a multivariate Gaussian as below,
, we can express this distribution as a multivariate Gaussian as below,
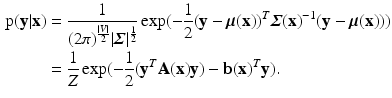
The parameters 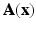 and
and 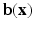 are dependent on the association and interaction potential definitions. In most classification tasks involving CRF’s the association potential is defined as the local class probability as provided by a generic classifier or a regressor [9]. Image synthesis being a regression task, we chose to model and extract both association and interaction potentials from a single regressor, in our case a regression tree. We define a quadratic association potential as
are dependent on the association and interaction potential definitions. In most classification tasks involving CRF’s the association potential is defined as the local class probability as provided by a generic classifier or a regressor [9]. Image synthesis being a regression task, we chose to model and extract both association and interaction potentials from a single regressor, in our case a regression tree. We define a quadratic association potential as
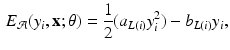
where 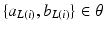 are the parameters defined at the leaf L(i). L(i) is the leaf where the feature vector
are the parameters defined at the leaf L(i). L(i) is the leaf where the feature vector 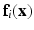 extracted for voxel i from the observed data
extracted for voxel i from the observed data 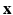 , lands after having been passed through successive nodes of a learned regression tree,
, lands after having been passed through successive nodes of a learned regression tree, 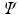 . The features and regression tree construction are described in Sect. 2.2.
. The features and regression tree construction are described in Sect. 2.2.
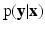 in terms of association potentials and interaction potentials is given as,
in terms of association potentials and interaction potentials is given as,![$$\begin{aligned} \mathrm {p}(\mathbf{y}| \mathbf{x}) = \frac{1}{Z}\exp [-\{\sum _{i\in V} E_{\mathcal {A}}(y_i, \mathbf{x}; \theta ) + \lambda \sum _{i \in V} \sum _{j \in \mathcal {N}_i} E_{\mathcal {I}}(y_i, y_j,\mathbf{x};\theta )\}]. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_58_Chapter_Equ1.gif)
(1)
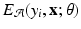 is called an association potential, defined using the parameter set
is called an association potential, defined using the parameter set 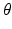 ,
, 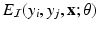 is called an interaction potential,
is called an interaction potential, 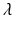 is a weighting factor, and Z is the partition function. If
is a weighting factor, and Z is the partition function. If 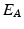 and
and 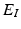 are defined as quadratic functions of
are defined as quadratic functions of 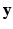 , we can express this distribution as a multivariate Gaussian as below,
, we can express this distribution as a multivariate Gaussian as below,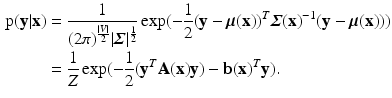
(2)
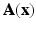 and
and 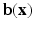 are dependent on the association and interaction potential definitions. In most classification tasks involving CRF’s the association potential is defined as the local class probability as provided by a generic classifier or a regressor [9]. Image synthesis being a regression task, we chose to model and extract both association and interaction potentials from a single regressor, in our case a regression tree. We define a quadratic association potential as
are dependent on the association and interaction potential definitions. In most classification tasks involving CRF’s the association potential is defined as the local class probability as provided by a generic classifier or a regressor [9]. Image synthesis being a regression task, we chose to model and extract both association and interaction potentials from a single regressor, in our case a regression tree. We define a quadratic association potential as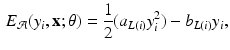
(3)
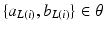 are the parameters defined at the leaf L(i). L(i) is the leaf where the feature vector
are the parameters defined at the leaf L(i). L(i) is the leaf where the feature vector 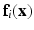 extracted for voxel i from the observed data
extracted for voxel i from the observed data 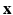 , lands after having been passed through successive nodes of a learned regression tree,
, lands after having been passed through successive nodes of a learned regression tree, 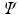 . The features and regression tree construction are described in Sect. 2.2.
. The features and regression tree construction are described in Sect. 2.2.The interaction potential usually acts as a smoothing term, but can also be designed in a more general manner. We define interaction potentials for each type of neighbor. A ‘neighbor type’ 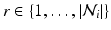 is given by a voxel i and one of its
is given by a voxel i and one of its 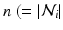 ) neighbors. For example, a neighborhood system with four neighbors (up, down, left, right) has four types of neighbors, and hence four types of edges. The complete set of edges E can be divided into non-intersecting subsets
) neighbors. For example, a neighborhood system with four neighbors (up, down, left, right) has four types of neighbors, and hence four types of edges. The complete set of edges E can be divided into non-intersecting subsets 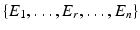 of edges of different types. Let the voxel j be such that
of edges of different types. Let the voxel j be such that 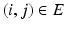 is a neighbor of type r, that is
is a neighbor of type r, that is 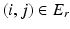 . Let the corresponding feature vectors
. Let the corresponding feature vectors 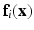 and
and 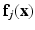 land in leaves L(i) and L(j) of the trained tree
land in leaves L(i) and L(j) of the trained tree 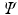 , respectively. The interaction potential is modeled as
, respectively. The interaction potential is modeled as
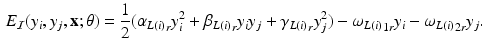
Let the set of leaves of the regression tree 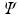 be
be 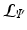 . Each leaf
. Each leaf 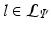 stores the set of parameters
stores the set of parameters 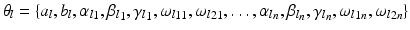 . The complete set of parameters is thus,
. The complete set of parameters is thus, 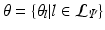 . Our approach bears similarity to the regression tree fields concept introduced in [7], where the authors create a separate regression tree for each neighbor type. Thus with a single association potential and a typical 3D neighborhood of 26 neighbors, they would need 27 separate trees to learn the model parameters. Training a large number of trees with large training sets makes the regression tree fields approach computationally expensive. It was especially not feasible in our application with large 3D images, more neighbors, and high dimensional feature vectors. We can however train multiple trees using bagging to create an ensemble of models to create an average, improved prediction. The training of a single regression tree is described in the next section.
. Our approach bears similarity to the regression tree fields concept introduced in [7], where the authors create a separate regression tree for each neighbor type. Thus with a single association potential and a typical 3D neighborhood of 26 neighbors, they would need 27 separate trees to learn the model parameters. Training a large number of trees with large training sets makes the regression tree fields approach computationally expensive. It was especially not feasible in our application with large 3D images, more neighbors, and high dimensional feature vectors. We can however train multiple trees using bagging to create an ensemble of models to create an average, improved prediction. The training of a single regression tree is described in the next section.
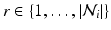 is given by a voxel i and one of its
is given by a voxel i and one of its 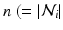 ) neighbors. For example, a neighborhood system with four neighbors (up, down, left, right) has four types of neighbors, and hence four types of edges. The complete set of edges E can be divided into non-intersecting subsets
) neighbors. For example, a neighborhood system with four neighbors (up, down, left, right) has four types of neighbors, and hence four types of edges. The complete set of edges E can be divided into non-intersecting subsets 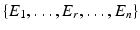 of edges of different types. Let the voxel j be such that
of edges of different types. Let the voxel j be such that 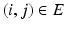 is a neighbor of type r, that is
is a neighbor of type r, that is 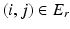 . Let the corresponding feature vectors
. Let the corresponding feature vectors 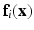 and
and 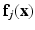 land in leaves L(i) and L(j) of the trained tree
land in leaves L(i) and L(j) of the trained tree 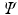 , respectively. The interaction potential is modeled as
, respectively. The interaction potential is modeled as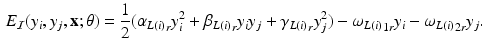
(4)
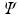 be
be 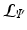 . Each leaf
. Each leaf 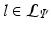 stores the set of parameters
stores the set of parameters 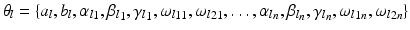 . The complete set of parameters is thus,
. The complete set of parameters is thus, 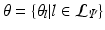 . Our approach bears similarity to the regression tree fields concept introduced in [7], where the authors create a separate regression tree for each neighbor type. Thus with a single association potential and a typical 3D neighborhood of 26 neighbors, they would need 27 separate trees to learn the model parameters. Training a large number of trees with large training sets makes the regression tree fields approach computationally expensive. It was especially not feasible in our application with large 3D images, more neighbors, and high dimensional feature vectors. We can however train multiple trees using bagging to create an ensemble of models to create an average, improved prediction. The training of a single regression tree is described in the next section.
. Our approach bears similarity to the regression tree fields concept introduced in [7], where the authors create a separate regression tree for each neighbor type. Thus with a single association potential and a typical 3D neighborhood of 26 neighbors, they would need 27 separate trees to learn the model parameters. Training a large number of trees with large training sets makes the regression tree fields approach computationally expensive. It was especially not feasible in our application with large 3D images, more neighbors, and high dimensional feature vectors. We can however train multiple trees using bagging to create an ensemble of models to create an average, improved prediction. The training of a single regression tree is described in the next section.2.2 Learning a Regression Tree
As mentioned before, let 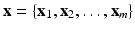 be a collection of co-registered images, generated by modalities
be a collection of co-registered images, generated by modalities 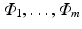 , respectively. The image synthesis task entails predicting the image
, respectively. The image synthesis task entails predicting the image 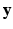 of a target modality
of a target modality 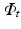 . The training data thus consists of known co-registered pair of
. The training data thus consists of known co-registered pair of 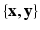 . At each voxel location i, we extract features
. At each voxel location i, we extract features 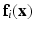 , derived from
, derived from 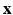 . For our experiments we use two types of features, (1) small, local patches, (2) context descriptors. A small 3D patch, denoted by
. For our experiments we use two types of features, (1) small, local patches, (2) context descriptors. A small 3D patch, denoted by ![$$\mathbf{p}_i(\mathbf{x}) = [\mathbf{p}_i(\mathbf{x}_1), \ldots , \mathbf{p}_i(\mathbf{x}_m)]$$](/wp-content/uploads/2016/09/A339424_1_En_58_Chapter_IEq65.gif) , where the size of the patch is typically
, where the size of the patch is typically 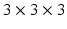 and provides us with local intensity information.
and provides us with local intensity information.
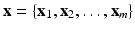 be a collection of co-registered images, generated by modalities
be a collection of co-registered images, generated by modalities 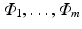 , respectively. The image synthesis task entails predicting the image
, respectively. The image synthesis task entails predicting the image 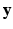 of a target modality
of a target modality 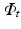 . The training data thus consists of known co-registered pair of
. The training data thus consists of known co-registered pair of 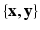 . At each voxel location i, we extract features
. At each voxel location i, we extract features 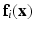 , derived from
, derived from 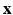 . For our experiments we use two types of features, (1) small, local patches, (2) context descriptors. A small 3D patch, denoted by
. For our experiments we use two types of features, (1) small, local patches, (2) context descriptors. A small 3D patch, denoted by ![$$\mathbf{p}_i(\mathbf{x}) = [\mathbf{p}_i(\mathbf{x}_1), \ldots , \mathbf{p}_i(\mathbf{x}_m)]$$](/wp-content/uploads/2016/09/A339424_1_En_58_Chapter_IEq65.gif) , where the size of the patch is typically
, where the size of the patch is typically 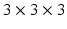 and provides us with local intensity information.
and provides us with local intensity information.We construct the context descriptors as follows. The brain images are rigidly aligned to the MNI coordinate system [4] with the center of the brain approximately at the center of the image. Thus for each voxel we can find out the unit vector 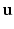 from the voxel i to the origin. We can define 8 directions by rotating the component of
from the voxel i to the origin. We can define 8 directions by rotating the component of 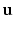 in the axial plane by angles
in the axial plane by angles 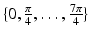 . In each of these directions, we select average intensities of cubic regions of cube-widths
. In each of these directions, we select average intensities of cubic regions of cube-widths 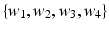 at four different radii
at four different radii 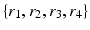 respectively. This becomes a 32-dimensional descriptor of the spatial context surrounding voxel i. In our experiments we used
respectively. This becomes a 32-dimensional descriptor of the spatial context surrounding voxel i. In our experiments we used 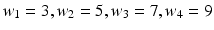 and
and 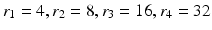 . These values were chosen empirically. We denote this context descriptor by
. These values were chosen empirically. We denote this context descriptor by 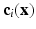 . The final feature vector is thus
. The final feature vector is thus ![$$\mathbf{f}_i(\mathbf{x}) = [\mathbf{p}_i(\mathbf{x}),\mathbf{c}_i(\mathbf{x})]$$](/wp-content/uploads/2016/09/A339424_1_En_58_Chapter_IEq75.gif) .
. 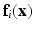 is paired with the voxel intensity
is paired with the voxel intensity 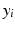 at i in the target modality image
at i in the target modality image 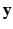 to create training data pairs
to create training data pairs 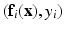 . We train the regression tree
. We train the regression tree 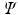 on this training data using the algorithm described in [2]. Once the tree is constructed, we initialize
on this training data using the algorithm described in [2]. Once the tree is constructed, we initialize 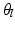 at each of the leaves
at each of the leaves 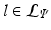 .
. 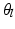 is estimated by a pseudo-likelihood maximization approach.
is estimated by a pseudo-likelihood maximization approach.
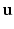 from the voxel i to the origin. We can define 8 directions by rotating the component of
from the voxel i to the origin. We can define 8 directions by rotating the component of 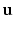 in the axial plane by angles
in the axial plane by angles 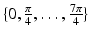 . In each of these directions, we select average intensities of cubic regions of cube-widths
. In each of these directions, we select average intensities of cubic regions of cube-widths 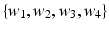 at four different radii
at four different radii 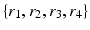 respectively. This becomes a 32-dimensional descriptor of the spatial context surrounding voxel i. In our experiments we used
respectively. This becomes a 32-dimensional descriptor of the spatial context surrounding voxel i. In our experiments we used 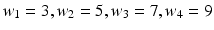 and
and 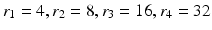 . These values were chosen empirically. We denote this context descriptor by
. These values were chosen empirically. We denote this context descriptor by 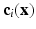 . The final feature vector is thus
. The final feature vector is thus ![$$\mathbf{f}_i(\mathbf{x}) = [\mathbf{p}_i(\mathbf{x}),\mathbf{c}_i(\mathbf{x})]$$](/wp-content/uploads/2016/09/A339424_1_En_58_Chapter_IEq75.gif) .
. 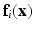 is paired with the voxel intensity
is paired with the voxel intensity 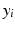 at i in the target modality image
at i in the target modality image 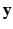 to create training data pairs
to create training data pairs 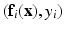 . We train the regression tree
. We train the regression tree 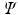 on this training data using the algorithm described in [2]. Once the tree is constructed, we initialize
on this training data using the algorithm described in [2]. Once the tree is constructed, we initialize 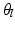 at each of the leaves
at each of the leaves 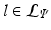 .
. 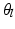 is estimated by a pseudo-likelihood maximization approach.
is estimated by a pseudo-likelihood maximization approach.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




