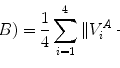and Dorin Comaniciu1
(1)
Imaging and Computer Vision, Siemens Corporate Technology, Princeton, NJ, USA
Abstract
In this chapter, we present the constrained MSL to exploit correlations learned from the training set to increase the efficiency of the computational framework. The prior distribution of the object position is learned based on the statistics of the distance from the object center to volume border, and the test hypotheses of the orientation and scale are generated using an example-based sampling strategy from the training set. Furthermore, we employ the quaternion formulation for 3D orientation representation and distance measurement to overcome the limitations of Euler angles in the original MSL. Extensive comparison experiments are performed on three 3D anatomical structure detection problems in medical images, namely, liver detection in Computed Tomography (CT) volumes, and left ventricle detection in both CT and ultrasound volumes. They show that constrained MSL can improve the detection speed up to 14 times relative to the original MSL, while achieving comparable or better detection accuracy. It takes less than half a second to detect a typical 3D anatomical structure in a volume.
4.1 Introduction
In the previous chapters we showed how the computational framework of Marginal Space Learning (MSL) achieves efficient and robust object detection by selectively focusing on the classification in marginal spaces of increasing dimensionality. The MSL strategy is to start object detection in a lower dimension space, such as the position space, and add more and more parameters in the subsequent detection stages, by also including the object’s orientation, scale and non-rigid deformation.
As the title of this chapter suggests, further constraints imposed on marginal spaces can increase the efficiency of the MSL process. First, from the training set we compute the distribution range of each parameter and uniformly sample in that range to generate test hypotheses. Since the location/center of an object cannot be arbitrarily close to the volume border, we can safely skip those hypotheses around volume border during the object pose estimation.
Second, in many applications the pose parameters are not independent. A large organ, for example, is likely to have larger values in all three directions. We can exploit such correlations among pose parameters to reduce the number of testing hypotheses and implicitly increase the MSL efficiency [14, 15] . We rely on the joint distribution of parameters in the training set to drive the hypothesis generation and sample only the regions with high probabilities. The estimation of the joint distribution is, however difficult, due to the limited number of positive samples, typically hundreds. Therefore, to generate testing hypotheses, we use uniform kernels in the joint parameter space, centered on the training samples, a process called example-based sampling [2, 16]. We start by uniformly sampling the marginal space to get a large set, S u . For each training sample, we add its neighboring hypotheses in S u to the test set S t . Repeating the above process for all training samples and consolidating redundant hypotheses in S t , we derive a much smaller test set than S u .
The constrained marginal space learning defined as above improves the detection speed by an order of magnitude when compared to the standard MSL. Besides the speed-up, constraining the search to a small valid region can reduce the likelihood of detection outliers, therefore improving the detection accuracy.
Let us now discuss the representations and sampling in the orientation space. As discussed in Chap. 2, for the original MSL we used three Euler angles to represent the 3D orientation space , an approach that has several limitations: (1) There are multiple sets of values that can yield the same orientation, leading to a fundamental ambiguity . (2) The Euclidean distance in the Euler angle space is used in the original MSL as the distance measurement between two orientations. However, since the mapping from Euler angles to orientation space is not distance-preserving, uniform sampling in the Euler angle space is not uniform in the orientation space [4, 7], this effect introducing degradations in the results.
In this chapter we introduce the use of quaternions [4] to overcome all the above limitations. Quaternions provide a straightforward orientation representation that can effectively handle the rotation problem and help calculating the correct distance between two orientations.
In summary, we make two major improvements to the original MSL.
1.
After analyzing the challenges of Euler angles for 3D orientation representation, we employ quaternions to overcome the limitations of Euler angles.
2.
We develop efficient ways to further constrain the search spaces in the MSL and improve the detection speed by an order of magnitude. As a result, it takes less than half a second to detect a 3D anatomical structure in a typical data volume.
The remainder of this chapter is organized as follows. In Sect. 4.2, we compare Euler angles and quaternions for 3D orientation representation and discuss the limitations of Euler angles as used in the original MSL. We also show how to uniformly sample an orientation space to generate orientation hypotheses and calculate the mean orientation to aggregate multiple top candidates into a single estimate. Section 4.3 presents our approach to constraining the search space in the MSL. Extensive comparison experiments on large medical datasets in Sect. 4.4 demonstrate the efficiency of the constrained MSL. This chapter concludes with Sect. 4.5.
4.2 3D Orientation
In this section, we first analyze the drawbacks of Euler angles for 3D orientation representation in the original MSL and then propose to use quaternions to solve all the limitations of Euler angles.
4.2.1 Representation with Euler Angles
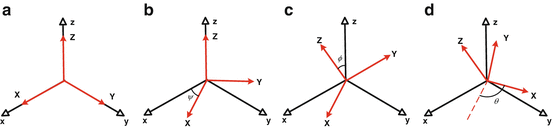
Fig. 4.1
Euler angles in the ZXZ convention. (a) Initial orientation with x–y–z representing a reference coordinate system and X–Y –Z representing the rotating coordinate system. (b) After rotation around the Z axis with an amount ψ. (c) After rotation around the X axis with an amount ϕ. (d) Final orientation after rotation around the Z axis with an amount θ
It is well known that 3D orientation has three degrees of freedom and can be represented as three Euler angles. An advantage of Euler angles is that they have an intuitive physical meaning. For example, an orientation with Euler angles of ψ, ϕ, and θ in the ZXZ convention is achieved by rotating the original coordinate system around the Z axis with an amount ψ, followed by a rotation around the X axis with an amount ϕ, and lastly a rotation around the Z axis again with an amount θ. Figure 4.1 shows each rotation step of the above example. The rotation operation is not commutable. That means we cannot change the order of rotations. The rotations can either occur about the axes of the fixed coordinate system (extrinsic rotations) or about the axes of a rotating coordinate system, which is initially aligned with the fixed one and modifies its orientation after each elemental rotation (intrinsic rotations) . From now on, we will focus on intrinsic rotations, as shown in Fig. 4.1.
To train a classifier to distinguish correct orientation estimates from wrong ones, we need to provide both positive and negative training samples. The Euclidean distance 1 in the Euler angle space can be used to measure the distance of a hypothesis O h = (ψ h , ϕ h , θ h ) to the ground truth O t = (ψ t , ϕ t , θ t )
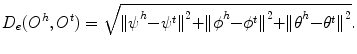
If the distance is less than a threshold, it corresponds to a positive sample, otherwise to a negative one. Though convenient, the Euclidean distance is not a good distance measurement of orientations. There are multiple sets of Euler angles that yield the same orientation, leading to a fundamental ambiguity. For example, Euler angles (α, 0, β) and (γ, 0, θ) in the ZXZ convention represent the same orientation when 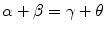 . That means two close orientations may have a large distance in the Euler angle space. Therefore, the collected positive and negative sets may be confusing, which makes the learning difficult.
. That means two close orientations may have a large distance in the Euler angle space. Therefore, the collected positive and negative sets may be confusing, which makes the learning difficult.
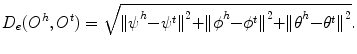
(4.1)
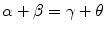 . That means two close orientations may have a large distance in the Euler angle space. Therefore, the collected positive and negative sets may be confusing, which makes the learning difficult.
. That means two close orientations may have a large distance in the Euler angle space. Therefore, the collected positive and negative sets may be confusing, which makes the learning difficult.To estimate the orientation of an object, we need to uniformly sample the orientation space to generate a set of hypotheses . Each hypothesis is then tested with the trained classifier to pick the best one. However, uniform sampling of the Euler angle space under the Euclidean distance is not truly uniform in the orientation space [7].
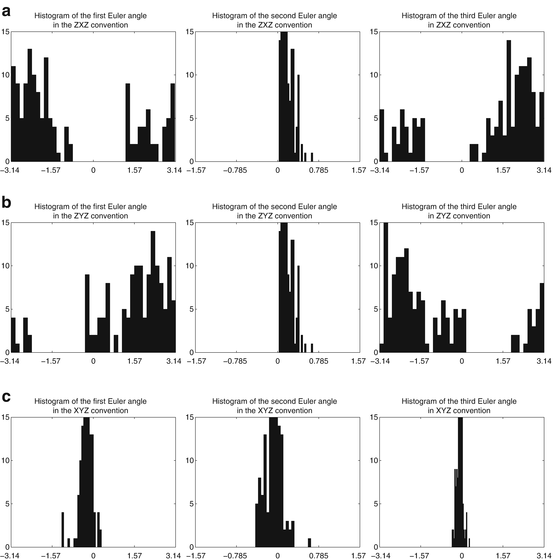
Fig. 4.2
Histograms of three Euler angles of the left ventricle orientation in ultrasound volumes in (a) the ZXZ convention, (b) the ZYZ convention, and (c) the XYZ convention
Another drawback of using Euler angles is that there are 12 possible conventions and a handful are widely used [7]. In the original MSL as presented in Chap. 2, the range of Euler angles is computed from a training set. Each Euler angle is then uniformly sampled within that range to generate hypotheses. Different conventions may give quite different search ranges. For example, if the rotation is only around the y axis, the XYZ convention (where two Euler angles are zero) is more compact than the ZXZ conventions since the latter needs three rotations to generate a pure rotation around the y axis. Figure 4.2 shows the histograms of the Euler angles with the ZXZ , ZYZ , and XYZ conventions for the left ventricle orientation in ultrasound volumes (see Sect. 4.4.3). In this case, the representation with the XYZ convention is more compact. However, for the application of heart chamber detection in cardiac CT volumes (see Sect. 4.4.2), we find that the ZXZ convention is more efficient than the XYZ convention to represent the Euler angle distribution range. In practice, for a new application, we need to try different conventions to select the most compact one.
In summary, previous use of Euler angles for orientation representation in Chap. 2 presents the following challenges:
1.
Due to the inherent ambiguity in Euler angle representation, the same orientation can be represented with multiple value sets .
2.
The Euclidean distance in the Euler angle space is not a good distance measurement of orientations.
3.
Uniform sampling of the Euler angle space is not uniform in the orientation space due to the use of a wrong distance measurement.
4.
Among many Euler angle conventions, we need to manually select the convention that represents the search range most compactly.
5.
Each Euler angle is uniformly sampled independently to generate orientation hypotheses, without exploiting the correlation among them. Therefore, many more hypotheses are tested than necessary during object detection.
4.2.2 Representation with Quaternions
In this work, we use quaternions to overcome the drawbacks of the Euler angles as used in the original MSL. Introduced in mid-1800s by Hamilton, quaternions provide an elegant conceptual framework, which can solve many problems involving rotations [4]. A quaternion is represented by four numbers
![$$\displaystyle{ \mathbf{q} = [w,x,y,z], }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ2.gif)
or as a scalar and a vector
![$$\displaystyle{ \mathbf{q} = [s,\mathbf{v}]. }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ3.gif)
In the scalar-vector representation , multiplication of two quaternions becomes
![$$\displaystyle{ \mathbf{q_{1}}\mathbf{q_{2}} = [s_{1}s_{2} -\mathbf{v_{1}}.\mathbf{v_{2}},\quad s_{1}\mathbf{v_{2}} + s_{2}\mathbf{v_{1}} + \mathbf{v_{1}} \times \mathbf{v_{2}}], }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ4.gif)
where v 1. v 2 is the vector inner-product and v 1 ×v 2 is the vector cross-product. The multiplication of two quaternions is also a quaternion.
![$$\displaystyle{ \mathbf{q} = [w,x,y,z], }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ2.gif)
(4.2)
![$$\displaystyle{ \mathbf{q} = [s,\mathbf{v}]. }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ3.gif)
(4.3)
![$$\displaystyle{ \mathbf{q_{1}}\mathbf{q_{2}} = [s_{1}s_{2} -\mathbf{v_{1}}.\mathbf{v_{2}},\quad s_{1}\mathbf{v_{2}} + s_{2}\mathbf{v_{1}} + \mathbf{v_{1}} \times \mathbf{v_{2}}], }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ4.gif)
(4.4)
To represent an orientation, we use unit quaternions ,
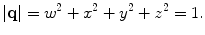
A unit quaternion also has three degrees of freedom, the same as the Euler angles. The rotation matrix , R, can be represented by unit quaternions as
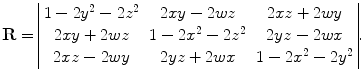
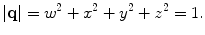
(4.5)
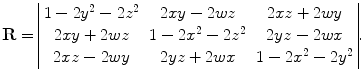
(4.6)
A unit quaternion can also be represented in the scalar-vector form as
![$$\displaystyle{ \mathbf{q} = [\cos (\theta /2),\mathbf{v}\sin (\theta /2)], }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ7.gif)
where v is a three-dimensional unit vector. Given a quaternion p, if we left-multiply it with ![$$\mathbf{q} = [\cos (\theta /2),\mathbf{v}\sin (\theta /2)]$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_IEq2.gif) , we get a new quaternion qp. The physical meaning of this operation is that qp represents the orientation after we rotate p around axis v with the amount of rotation θ [4]. The conjugate of a quaternion is defined as
, we get a new quaternion qp. The physical meaning of this operation is that qp represents the orientation after we rotate p around axis v with the amount of rotation θ [4]. The conjugate of a quaternion is defined as
![$$\displaystyle{ \overline{\mathbf{q}} = [w,-x,-y,-z] = [\cos (-\theta /2),\mathbf{v}\sin (-\theta /2)]. }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ8.gif)
Here, 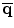 represents a rotation around axis v with an amount −θ.
represents a rotation around axis v with an amount −θ.
![$$\displaystyle{ \mathbf{q} = [\cos (\theta /2),\mathbf{v}\sin (\theta /2)], }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ7.gif)
(4.7)
![$$\mathbf{q} = [\cos (\theta /2),\mathbf{v}\sin (\theta /2)]$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_IEq2.gif) , we get a new quaternion qp. The physical meaning of this operation is that qp represents the orientation after we rotate p around axis v with the amount of rotation θ [4]. The conjugate of a quaternion is defined as
, we get a new quaternion qp. The physical meaning of this operation is that qp represents the orientation after we rotate p around axis v with the amount of rotation θ [4]. The conjugate of a quaternion is defined as![$$\displaystyle{ \overline{\mathbf{q}} = [w,-x,-y,-z] = [\cos (-\theta /2),\mathbf{v}\sin (-\theta /2)]. }$$](/wp-content/uploads/2016/08/A314110_1_En_4_Chapter_Equ8.gif)
(4.8)
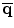 represents a rotation around axis v with an amount −θ.
represents a rotation around axis v with an amount −θ.Given two orientations, we can rotate one around an axis to align it to the other [11]. The amount of rotation provides a natural definition of the distance between two orientations. Using quaternions, we can calculate the amount of rotation between two orientations easily. The rotation, 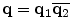 , moves q 2 to q 1. Therefore, the amount of rotation between quaternions q 1 and q 2 using the scalar-vector representation in Eq. (4.3) is
, moves q 2 to q 1. Therefore, the amount of rotation between quaternions q 1 and q 2 using the scalar-vector representation in Eq. (4.3) is
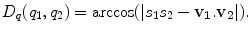
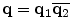 , moves q 2 to q 1. Therefore, the amount of rotation between quaternions q 1 and q 2 using the scalar-vector representation in Eq. (4.3) is
, moves q 2 to q 1. Therefore, the amount of rotation between quaternions q 1 and q 2 using the scalar-vector representation in Eq. (4.3) is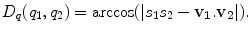
(4.9)
For comparison, the measurement using the Euclidean distance in the Euler angle space D e (Eq. (4.1)) is often larger than the quaternion-based distance D q . However, for some cases, D e (O 1, O 2) = D q (O 1, O 2). Suppose the XYZ convention is used and the only rotation is around the x axis in an amount less than 180 degrees. In this case, the last two Euler angles are zero. The Euclidean distance in the Euler angle space measures the rotation around the x axis, which is the same to the quaternion distance defined in Eq. (4.9).
4.2.3 Uniform Sampling of 3D Orientation Space
In MSL, we need to generate a set of discrete orientation samples, which are uniformly distributed, as test hypotheses. The problem of uniform sampling can be formulated as, given N sample orientations, we want to distribute them as uniformly as possible. We can define “a covering radius, α, as the maximum rotation needed to align an arbitrary orientation with one of the sample orientations” [4] . For uniform sampling, we want to find an optimal configuration of N sample orientations that gives the smallest α. The optimization procedure is difficult in practice, an interested reader is referred to [4] for more details. A few near-optimal configurations for some N’s are listed in Table 4.1 and they are available for download from website http://charles.karney.info/orientation/.
Table 4.1
A few near-optimal uniformly sampled 3D orientation sets. Row N lists the number of orientations in each set and row α lists the covering radius. All the orientation sets are available for download from http://charles.karney.info/orientation/
Name | c48u1 | c600v | c48n9 | c600vc | c48u27 | c48u83 | c48u181 |
|---|---|---|---|---|---|---|---|
N | 24 | 60 | 216 | 360 | 648 | 1992 | 4344 |
α (∘) | 62.80 | 44.48 | 33.48 | 36.47 | 20.83 | 16.29 | 12.29 |
Name | c48n309 | c48n527 | c48u815 | c48u1153 | c48u1201 | c48u1641 | c48u2219 |
N | 7416 | 12648 | 19560 | 27672 | 28824 | 39384 | 53256 |
α (∘) | 9.72 | 8.17 | 7.40 | 6.60 | 6.48 | 5.75 | 5.27 |
Name | 48u2947 | c48u3733 | c48u4749 | c48u5879 | c48u7111 | c48u8649 | |
N | 70728 | 89592 | 113976 | 141096 | 170664 | 207576 | |
α (∘) | 4.71 | 4.37 | 4.00 | 3.74 | 3.53 | 3.26 |
Since the orientation space has three dimensions, reducing the covering radius α by a half increases the number of samples roughly by a factor of eight. To achieve a reasonable trade-off between speed and accuracy, orientation set c48n309 with α = 9. 72∘ is used for most of our 3D object detection problems. Orientation sets with more dense resolutions up to α = 0. 646∘ are also available from website http://charles.karney.info/orientation/. However, the smallest orientation difference our machine learning based estimator can distinguish cannot approach zero. The actual lower bound is determined by not only the power of the classifier, but also other factors, e.g., the voxel resolution and the ambiguity of orientation definition (which is often affected by the amount of nonrigid deformation of the target object across patients or different scans of the same patients). For rigid objects with less variation across patients, a more densely sampled orientation set may be used if the requirement of orientation estimation accuracy is high. For example, in [5, 6], the orientation of the intervertebral disk needs to be estimated accurately from a low resolution scout scan to set acquisition slice orientation for a high resolution scan. In that application, we used orientation set c48u8649 with α = 3. 26∘ and the actual mean orientation estimation error from automatic detection was 3. 9∘, only slightly higher than the sampling resolution.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree