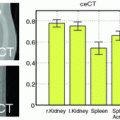
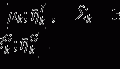Fig. 1.
An overview of the MCNN. Our approach first extracts multiple nodule patches to capture the wide range of nodule variability from input CT images. The obtained patches are then fed into the networks simultaneously to compute discriminative features. Finally, our approach applies a classifier to label the input nodule malignancy.
In this paper, we study the problem of lung nodule diagnostic classification based on thoracic CT scans. In contrast to the current methods primarily relying on nodule segmentation and textural feature descriptors for the classification task, we propose a hierarchical learning framework to capture the nodule heterogeneity by utilizing Convolutional Neural Networks (CNN) to extract features (as illustrated in Fig. 1). The learned features can be readily combined with state-of-the-art classifiers (e.g., Support Vector Machine (SVM) and Random Forest (RF)) for related Computer-Aided Diagnoses (CADs). Our method achieves 86.84 % accuracy on nodule classification using only nodule patches. We also observe that the proposed method is robust against noisy corruption—the classification performance is quite stable at different levels of noise inputs, indicating a well generalized property.
Contributions. We introduced an MCNN model to tackle the lung nodule diagnostic classification without delineation on nodule morphology and explored a hierarchical representation from raw patches for lung nodule classification. Our methodological contribution is three-fold:
Related Work. Image-based lung nodule analysis is normally performed with nodule segmentation [5], feature extraction [2], and labelling nodule categories [8, 17, 19]. Way et al. [19] first segmented the nodules and then extracted texture features to train a linear discriminant classifier. El-Baz et al. [5] used shape analysis for diagnosing malignant lung nodules. Han et al. [8] used 3-D texture feature analysis for the diagnosis of pulmonary nodules by considering extended neighbouring structures. However, all of these mentioned methods relied on nodule segmentation as a prerequisite for nodule feature extraction. Notably, automated nodule segmentation can affect classification since segmentation usually depends on initialization, such as region growing and level set methods. Working on these segmented regions may yield inaccurate features that lead to erroneous outputs.
Our MCNN take multi-scale raw nodule patches, rather than the segmented regions, providing evidence that information gained from the raw nodule patches is valuable for lung nodule diagnosis.
Our MCNN remove the need of any hand-crafted feature engineering work, such as nodule texture, shape compactness, and nodule sphericity. The MCNN can automatically learn the discriminative features.
Although it is challenging to directly deal with noisy data in nodule CT, we show that the proposed MCNN model is effective in capturing nodule characteristics in nodule diagnostic classification even with a high-level noisy corruption.
Descriptors of Histogram of Oriented Gradients (HOG) [4] and Local Binary Patterns (LBP) [13] are widely used for feature representation in medical image analysis. However, it is known that they are domain agnostic [15]. In other words, the required hyper-parameters make these approaches sensitive to specific tasks. For example, a repetitious parameter tuning is needed for the neighbourhood points in LBP and the size of the cell window in HOG.
Our work is conceptually similar to the massive training artificial neural network [17], which suggested a feasibility on learning knowledge from artificial neural networks. However, the work was an integrated classifier that required extra support from a 2-D Gaussian distribution for the decision-making, where an image-to-image mapping based on local pixels was learned. Our approach, without knowing any extra distributions, aims at feature extraction globally from the original nodule image space through stacked convolutional operations and max-pooling selections. In contrast to [17], our work is more computationally effective in reducing the feature dimensionality and resulting in highly discriminative features from hierarchical layers.
2 Learning Multi-scale Convolutional Neural Networks
Given a lung nodule CT image, our goal is to discover a set of globally discriminative features using the proposed MCNN model, which captures the essence of class-specific nodule information. The challenge is that the image space is extremely heterogeneous since both healthy tissues and nodules are included. In this work, we make full use of the CNN to learn discriminative features, and build three CNN in parallel to extract multi-scale features from nodules with different sizes. Details are given in this section.
2.1 Convolutional Neural Networks Architecture
Our Convolutional Neural Networks contain two convolutional layers, both of which are followed by a max-pooling layer, and a fully connected layer which represents the final output feature. The detailed structure of the network is shown in Fig. 2. From the input nodule patch to the final feature layer, the sizes of feature maps keep decreasing, which helps remove the potential redundant information in the original nodule patch and obtains discriminative features in nodule classification.
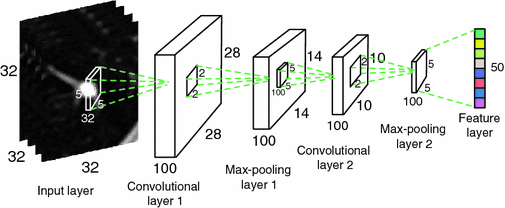

Fig. 2.
The structure of the Convolutional Neural Networks learned in our work. The numbers along each side of the cuboid indicate the dimensions of the feature maps. The inside cuboid represents the 3D convolution kernel and the inside square stands for the 2D pooling region. The number of the hidden neurons in the final feature layer is marked aside.
The network starts from a convolutional layer, which convolves the input feature map with a number of convolutional kernels and yields a corresponding number of output feature maps. Formally, the convolution operation between an input feature map f and a convolutional kernel h is defined by:
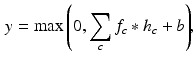
where 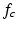 and
and 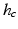 denote the cth slice from the feature map and that from the convolutional kernel respectively, and b is the bias scalar.
denote the cth slice from the feature map and that from the convolutional kernel respectively, and b is the bias scalar. 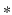 is the convolution operation. Both h and b are continuously learned in the training process. In order to perform a non-linear transformation from the input to the output space, we adopt the rectified linear unit (ReLu) non-linearity in Eq. 1 for each convolution [11]. It is expressed as
is the convolution operation. Both h and b are continuously learned in the training process. In order to perform a non-linear transformation from the input to the output space, we adopt the rectified linear unit (ReLu) non-linearity in Eq. 1 for each convolution [11]. It is expressed as 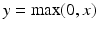 , where x is the convolution output.
, where x is the convolution output.
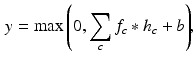
(1)
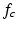 and
and 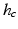 denote the cth slice from the feature map and that from the convolutional kernel respectively, and b is the bias scalar.
denote the cth slice from the feature map and that from the convolutional kernel respectively, and b is the bias scalar. 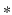 is the convolution operation. Both h and b are continuously learned in the training process. In order to perform a non-linear transformation from the input to the output space, we adopt the rectified linear unit (ReLu) non-linearity in Eq. 1 for each convolution [11]. It is expressed as
is the convolution operation. Both h and b are continuously learned in the training process. In order to perform a non-linear transformation from the input to the output space, we adopt the rectified linear unit (ReLu) non-linearity in Eq. 1 for each convolution [11]. It is expressed as 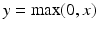 , where x is the convolution output.
, where x is the convolution output.Following the convolutional layer, a max-pooling layer is introduced to select feature subsets. It is formulated as
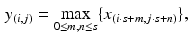
where s is the pooling size and x denotes the output of the convolutional layer. An advantage of using the max-pooling layer is its translation invariability which is especially helpful when different nodule images are not well-aligned.

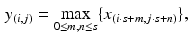
(2)

Fig. 3.
Nodule slice examples from a benign nodule patch (a) and a malignant nodule patch (b). The scales are 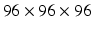 ,
, 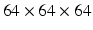 , and
, and 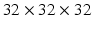 in pixel respectively.
in pixel respectively.
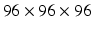 ,
, 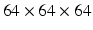 , and
, and 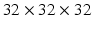 in pixel respectively.
in pixel respectively.2.2 Multi-scale Nodule Representation
Our idea of the multi-scale sampling strategy is motivated from the clinical fact that nodule sizes vary remarkably, ranging from less than 3 mm to more than 30 mm in the Lung Image Database Consortium and Image Database Resource Initiative (LIDC-IDRI) [3] datasets. In the proposed MCNN architecture, three CNN that take nodule patches from different scales (as shown in Fig. 3) as inputs are assembled in parallel. We briefly refer to the three CNN as 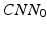 ,
, 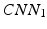 , and
, and 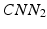 . In order to reduce the parameters of the MCNN, we follow the setting in [6] to share parameters among all the CNN. The resulting output of our MCNN is the concatenation of the three CNN outputs, forming the final discriminative feature vector, which will be directly fed to the final classifier without any feature reduction. We also follow the idea of deeply supervised networks (DSN) in [12] to construct our objective function. Unlike the traditional objective function in CNN, DSN introduced “companion objectives” [12] into the final objective function to alleviate the vanishing gradients problem so the training process can be fast and stable. The entire objective function is thus represented as
. In order to reduce the parameters of the MCNN, we follow the setting in [6] to share parameters among all the CNN. The resulting output of our MCNN is the concatenation of the three CNN outputs, forming the final discriminative feature vector, which will be directly fed to the final classifier without any feature reduction. We also follow the idea of deeply supervised networks (DSN) in [12] to construct our objective function. Unlike the traditional objective function in CNN, DSN introduced “companion objectives” [12] into the final objective function to alleviate the vanishing gradients problem so the training process can be fast and stable. The entire objective function is thus represented as
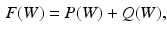
In our work, 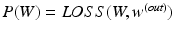 is the overall hinge loss function for the concatenated feature layer, and
is the overall hinge loss function for the concatenated feature layer, and 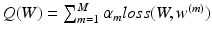 is the sum of the companion hinge loss functions from all CNN.
is the sum of the companion hinge loss functions from all CNN. 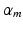 is the coefficient for the mth CNN. W denotes the combination of the weights from all of the CNN, while
is the coefficient for the mth CNN. W denotes the combination of the weights from all of the CNN, while 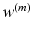 and
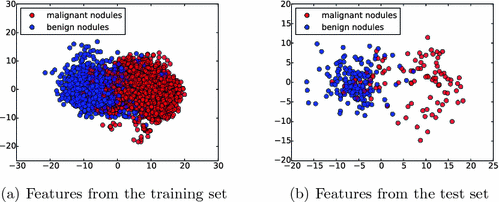
and 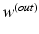 are the weights of the feature layer of the mth CNN and the weights of the final concatenated feature layer respectively. In this way, F(W) keeps each network optimized and also makes the assembly sensible. Figure 4 shows the concatenated features projected into a 2-D subspace. It shows that the proposed MCNN model is able to remove the redundant information in the original images and extract discriminative features.
are the weights of the feature layer of the mth CNN and the weights of the final concatenated feature layer respectively. In this way, F(W) keeps each network optimized and also makes the assembly sensible. Figure 4 shows the concatenated features projected into a 2-D subspace. It shows that the proposed MCNN model is able to remove the redundant information in the original images and extract discriminative features.
 ,
, 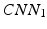 , and
, and 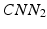 . In order to reduce the parameters of the MCNN, we follow the setting in [6] to share parameters among all the CNN. The resulting output of our MCNN is the concatenation of the three CNN outputs, forming the final discriminative feature vector, which will be directly fed to the final classifier without any feature reduction. We also follow the idea of deeply supervised networks (DSN) in [12] to construct our objective function. Unlike the traditional objective function in CNN, DSN introduced “companion objectives” [12] into the final objective function to alleviate the vanishing gradients problem so the training process can be fast and stable. The entire objective function is thus represented as
. In order to reduce the parameters of the MCNN, we follow the setting in [6] to share parameters among all the CNN. The resulting output of our MCNN is the concatenation of the three CNN outputs, forming the final discriminative feature vector, which will be directly fed to the final classifier without any feature reduction. We also follow the idea of deeply supervised networks (DSN) in [12] to construct our objective function. Unlike the traditional objective function in CNN, DSN introduced “companion objectives” [12] into the final objective function to alleviate the vanishing gradients problem so the training process can be fast and stable. The entire objective function is thus represented as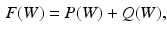
(3)
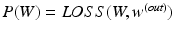 is the overall hinge loss function for the concatenated feature layer, and
is the overall hinge loss function for the concatenated feature layer, and 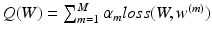 is the sum of the companion hinge loss functions from all CNN.
is the sum of the companion hinge loss functions from all CNN. 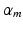 is the coefficient for the mth CNN. W denotes the combination of the weights from all of the CNN, while
is the coefficient for the mth CNN. W denotes the combination of the weights from all of the CNN, while 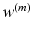 and
and 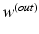 are the weights of the feature layer of the mth CNN and the weights of the final concatenated feature layer respectively. In this way, F(W) keeps each network optimized and also makes the assembly sensible. Figure 4 shows the concatenated features projected into a 2-D subspace. It shows that the proposed MCNN model is able to remove the redundant information in the original images and extract discriminative features.
are the weights of the feature layer of the mth CNN and the weights of the final concatenated feature layer respectively. In this way, F(W) keeps each network optimized and also makes the assembly sensible. Figure 4 shows the concatenated features projected into a 2-D subspace. It shows that the proposed MCNN model is able to remove the redundant information in the original images and extract discriminative features.
Fig. 4.
Feature visualization. The learned features by the MCNN from both training set (a) and test set (b) are illustrated by projecting them into a 2-D subspace with principal component analysis (PCA) [10].
3 Experiments
3.1 Datasets and Setup
We evaluated our method on the LIDC-IDRI datasets [3]. It consists of 1010 patients with lung cancer screening thoracic CT scans as well as mark-up annotated lesions. The nodules are rated from 1 to 5 by four experienced thoracic radiologists, indicating an increasing degree of malignancy (1 denotes low malignancy and 5 is high malignancy). In this study, we included nodules along with their annotated centers from the nodule report1. We chose the averaged malignancy rating for each nodule as in [8]. For those with an average score lower than 3, we labelled them as benign nodules; for those with an average score higher than 3, we labelled them as malignant nodules. We removed nodules with ambiguous IDs and those with an average score of 3. Overall, there were 880 benign nodules and 495 malignant nodules. Since the resolution of the images varied, we resampled those images to set the resolution to a fixed 0.5 mm/pixel along all three axes. Thus, the effect of resolution on the classification performance was removed. Then each nodule patch is cropped from the resampled CT image based on the marked nodule centers. The three scale inputs are 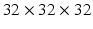 ,
,  , and
, and 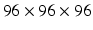 in pixels. Patches are all resampled to
in pixels. Patches are all resampled to 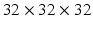 so that they can be uniformly fed into each CNN.
so that they can be uniformly fed into each CNN.
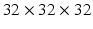 ,
,  , and
, and 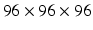 in pixels. Patches are all resampled to
in pixels. Patches are all resampled to 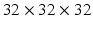 so that they can be uniformly fed into each CNN.
so that they can be uniformly fed into each CNN.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree