(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 2 consists of 23 problems that cover 7 sections dealing with various types of elastic scattering interactions that heavy and light charged particles can have with atoms of an absorber. The problems address the general category of Coulomb elastic scattering covering the practical and theoretical aspects of Coulomb scattering ranging from the seminal Geiger and Marsden experiment and Rutherford theory of alpha particle scattering on metallic foils through Mott scattering of electrons on nuclei of absorber to practical aspects of Molière multiple scattering.
The concepts addressed in this chapter are of great importance to modern physics because much of the current knowledge in atomic, nuclear, and particle physics has been derived from various Coulomb scattering experiments. Based on the unexpected angular distribution of scattered alpha particles, measured by Geiger and Marsden, Rutherford in 1912 proposed the current atomic model in which the atomic mass and the positive atomic charge are concentrated in the atomic nucleus that is at least four orders of magnitude smaller than the size of the atom.
Section 2.1 covers the basic characteristics of Coulomb scattering and the problem in Sect. 2.2 deals with the Geiger–Marsden experiment and introduces a comparison between the Thomson and Rutherford model of the atom. Problems of Sect. 2.3 deal with various aspects of Rutherford scattering, while Sect. 2.4 addresses the differential and total cross sections for Rutherford scattering. The problems of Sect. 2.5 concentrate on Mott scattering of electrons on nuclei of absorber and the problems of Sect. 2.6 cover the general aspects of Coulomb elastic scattering including characteristic scattering distance, minimum and maximum scattering angle, mean square scattering angle for single scattering. The last two problems of this chapter concentrate on mass scattering power (Sect. 2.6) and root mean square scattering angle for multiple scattering (Sect. 2.7).
Chapter 2 consists of 23 problems that cover 7 sections dealing with various types of elastic scattering interactions that heavy and light charged particles can have with atoms of an absorber. The problems address the general category of Coulomb elastic scattering covering the practical and theoretical aspects of Coulomb scattering ranging from the seminal Geiger and Marsden experiment and Rutherford theory of alpha particle scattering on metallic foils through Mott scattering of electrons on nuclei of absorber to practical aspects of Molière multiple scattering.
The concepts addressed in this chapter are of great importance to modern physics because much of the current knowledge in atomic, nuclear, and particle physics has been derived from various Coulomb scattering experiments. Based on the unexpected angular distribution of scattered alpha particles, measured by Geiger and Marsden, Rutherford in 1912 proposed the current atomic model in which the atomic mass and the positive atomic charge are concentrated in the atomic nucleus that is at least four orders of magnitude smaller than the size of the atom.
Section 2.1 covers the basic characteristics of Coulomb scattering and the problem in Sect. 2.2 deals with the Geiger–Marsden experiment and introduces a comparison between the Thomson and Rutherford model of the atom. Problems of Sect. 2.3 deal with various aspects of Rutherford scattering, while Sect. 2.4 addresses the differential and total cross sections for Rutherford scattering. The problems of Sect. 2.5 concentrate on Mott scattering of electrons on nuclei of absorber and the problems of Sect. 2.6 cover the general aspects of Coulomb elastic scattering including characteristic scattering distance, minimum and maximum scattering angle, mean square scattering angle for single scattering. The last two problems of this chapter concentrate on mass scattering power (Sect. 2.6) and root mean square scattering angle for multiple scattering (Sect. 2.7).
2.1 General Aspects of Coulomb Scattering
2.1.Q1 (60)
Coulomb scattering is a general term used to describe elastic Coulomb interaction between two charged particles: an energetic projectile and a stationary target.
(a)
In Table 2.1A provide a list of at least 5 elastic Coulomb scattering interactions and for each interaction give the projectile and the target.
(b)
Define Molière scattering.
Table 2.1A
Five most common elastic Coulomb scattering interactions
Coulomb scattering interaction | Projectile | Target | |
|---|---|---|---|
1 | |||
2 | |||
3 | |||
4 | |||
5 |
SOLUTION:
(a) Five most common elastic Coulomb scattering interactions are presented in Table 2.1B.
Table 2.1B
Five most common elastic Coulomb scattering interactions
Coulomb scattering interaction | Projectile | Target | |
|---|---|---|---|
1 | Rutherford scattering | Alpha particle | Nucleus |
2 | Ramsauer scattering | Electron (non-relativistic) | Atom or molecule |
3 | Mott scattering | Electron (relativistic) | Atomic nucleus |
4 | Møller scattering | Electron | Atomic orbital electron |
5 | Bhabha scattering | Positron | Atomic orbital electron |
(b) Molière scattering is defined as multiple scattering involving any one of the scattering interactions listed in Table 2.1B.
2.1.Q2 (61)
Much of the information on the structure and charge distribution of nuclei has been gathered through elastic Coulomb scattering experiments.
Discuss the two most important characteristics that a particle must possess when used as nuclear probe in elastic scattering experiments.
SOLUTION:
The two most important characteristics that a particle must possess when used as nuclear probe in elastic scattering experiments are: (1) de Broglie wavelength λ of the particle and (2) charge q of the particle.
(1) The particle serving as nuclear probe must have a de Broglie wavelength λ of the order of the size of the nucleus or smaller. The radius R of the nucleus (i.e., size of the nucleus) is estimated from ![$R = R_{0}\sqrt[3]{A}$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_IEq1.gif) , where R 0 is the nuclear radius constant (1.25 fm) and A is the atomic mass number of the nucleus.
, where R 0 is the nuclear radius constant (1.25 fm) and A is the atomic mass number of the nucleus.
![$R = R_{0}\sqrt[3]{A}$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_IEq1.gif) , where R 0 is the nuclear radius constant (1.25 fm) and A is the atomic mass number of the nucleus.
, where R 0 is the nuclear radius constant (1.25 fm) and A is the atomic mass number of the nucleus.The de Broglie wavelength of the nuclear probe projectile is calculated from the standard de Broglie expression λ=h/p, where p is the particle momentum derived in Prob. 34 as
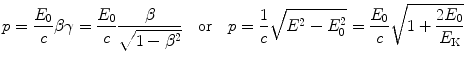
with
The de Broglie wavelength of the particle is thus given as
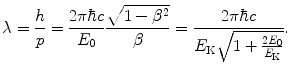
(2) The particle serving as nuclear probe must possess charge to enable an elastic Coulomb interaction between the nuclear probe (projectile) and the nucleus (target). Charge is also important in accelerating the particle to sufficiently high kinetic energy for the de Broglie wavelength λ to become of the order of, or smaller than, the size of the nucleus.
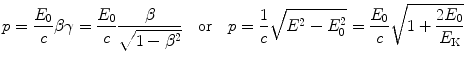
(2.1)
E
total energy of the particle.
E K
kinetic energy of the particle (E K=E−E 0).
E 0
rest energy of the particle.
γ
Lorentz factor of the particle.
β
velocity of the particle normalized to the speed of light c in vacuum.
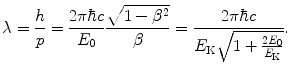
(2.2)
2.1.Q3 (62)
The distance of closest approach D α−N in a head-on collision between an α particle of kinetic energy E K and an atomic nucleus is calculated from conservation of energy considerations whereby we equate the α particle kinetic energy E K at large (∞) distance from the nucleus with repulsive Coulomb potential energy E P when the α particle is at a distance D α−N from the nucleus. D α−N is then given as follows
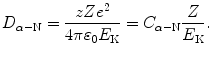
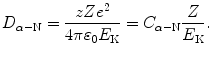
(2.3)
(a)
Determine the constant C α−N for alpha (α) particle scattering and use it to calculate D α−N for scattering of 5.5 MeV α particles (z=2) on gold nucleus (Z=79, A=197).
(b)
Plot D α−N against E K for α particle scattering on gold nuclei in the kinetic energy E K range from 1 MeV to 40 MeV.
(c)
Compare D α−N of (a) with the radius R Au of the gold nucleus and determine at what kinetic energy E K would the α particle just penetrate the gold nucleus.
SOLUTION:
(a) Constant C α−N for α particle scattering is calculated from (2.3) as follows
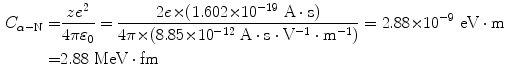
and D α−N in terms of C α−N for scattering of 5.5 MeV α particle on gold nucleus is given as
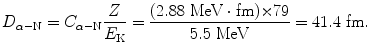
To see whether or not the α particle of initial kinetic energy (E K)i=5.5 MeV can penetrate the gold nucleus we estimate the radius R Au of the gold nucleus with the following relationship
![$$ R(A) = R_{\mathrm{Au}} = R_{0}\sqrt[3]{A} = (1.25\ \mathrm{fm}) {\times} \sqrt[3]{197} = 7.3\ \mathrm{fm}, $$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ6.gif)
where R 0 is the nuclear radius constant (T1.26). Since R Au of (2.6) is significantly smaller than D α−N of (2.5), we conclude that (E K)i=5.5 MeV α particle does not penetrate the gold nucleus.
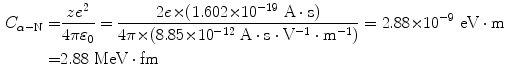
(2.4)
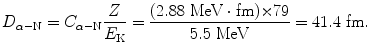
(2.5)
![$$ R(A) = R_{\mathrm{Au}} = R_{0}\sqrt[3]{A} = (1.25\ \mathrm{fm}) {\times} \sqrt[3]{197} = 7.3\ \mathrm{fm}, $$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ6.gif)
(2.6)
(b) Figure 2.1 shows a plot of the distance of closest approach D α−N in a direct-hit collision of an α particle with a gold nucleus in the initial kinetic energy (E K)i range from 1 MeV to 40 MeV. As shown in (2.5), D α−N in general is linearly proportional to the atomic number Z of the absorber and inversely proportional to the kinetic energy (E K)i of the α particle, and constant C α−N is equal to 2.88 MeV⋅fm, as determined in (2.4) for all absorbers Z.
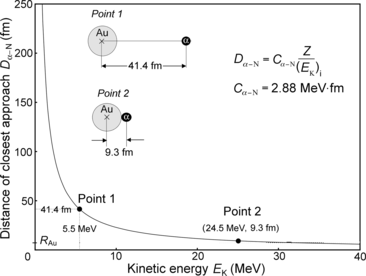

Fig. 2.1
Distance of closest approach D α−N against kinetic energy E K of the α particle in a direct-hit (θ=π) collision between α particle and gold nucleus (Z=79). Point 1 on the curve represents D α−N of 41.4 fm for (E K)i of 5.5 MeV; point 2 represents (E K)i of 24.5 MeV for D α−N of 9.3 fm
(c) In (a) we showed that the distance of closest approach D α−N for a 5.5 MeV α particle in a head-on collision with gold nucleus is 41.4 fm, while the radius R Au of gold nucleus is 7.3 fm. We assume that at point of initial penetration of the gold nucleus the distance D α−N between the center of the gold nucleus and the center of the α particle is simply the sum of their radii, i.e., D α−N=R α +R Au=9.3 fm where we used ![$R_{\alpha} = R_{0}\sqrt[3]{A} = (1.25\ \mathrm{fm}) {\times} \sqrt[3]{4} \approx 2~\mathrm{fm}$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_IEq2.gif) for radius of α particle.
for radius of α particle.
![$R_{\alpha} = R_{0}\sqrt[3]{A} = (1.25\ \mathrm{fm}) {\times} \sqrt[3]{4} \approx 2~\mathrm{fm}$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_IEq2.gif) for radius of α particle.
for radius of α particle.We now rearrange (2.5) to calculate the initial kinetic energy (E K)i that an α particle must possess to attain a distance of closest approach D α−N of 9.3 fm in a head-on collision
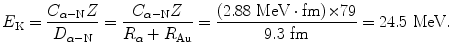
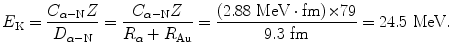
(2.7)
2.2 Geiger-Marsden Experiment
2.2.Q1 (63)
(a)
Write short notes on: (1) Thomson “plum pudding” model of the atom and (2) Rutherford nuclear model of the atom and for each model present a sketch.
(b)
Discuss the expected angular distribution of α particles in Geiger-Marsden scattering experiment assuming the validity of Thomson “plum-pudding” model of the atom.
(c)
Discuss the expected angular distribution of α particles in Geiger-Marsden scattering experiment assuming the validity of Rutherford nuclear model of the atom.
(d)
A collimated beam of α particles emitted from a Po-210 source (E K=5.4 MeV) strikes a 2.5 μm gold foil (Z=79, A=197 g/mol, and ρ=19.3 g/cm3). Calculate the probability of an α particle to be scattered at angles between Θ 1=10∘ and Θ 2=12∘ according to: (1) Thomson “plum pudding” model of the atom and (2) Rutherford nuclear model of the atom.
SOLUTION:
(a) In 1898 Joseph J. Thomson, who is also credited with the discovery of the electron in 1897, proposed an atomic model in which the mass of the atom is distributed uniformly over the volume of the atom that has a radius of the order of 1 Å and negatively charged electrons are dispersed uniformly within a continuous spherical distribution of positive charge. Thus, positive charges and the negative (electron) charges of an atom are distributed uniformly over the atomic volume (“plum pudding” model) to make the atom neutral on the outside [see Fig. 2.2(A)].
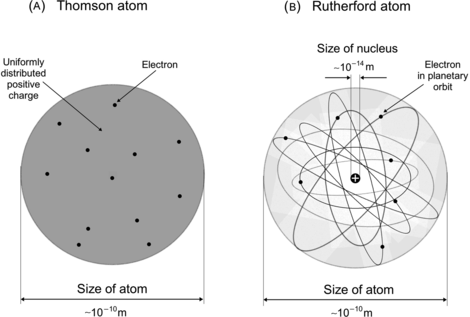

Fig. 2.2
Schematic diagram of two atomic models: (A) Thomson model and (B) Rutherford model
Based on α scattering results that Geiger and Marsden carried out with gold foils, Ernest Rutherford in 1911 proposed a completely new atomic model that was much better suited than Thomson model to explain the peculiar α scattering experimental results obtained by Geiger and Marsden. In the Rutherford nuclear model, essentially all atomic mass is concentrated in a small nucleus with the size of the order of few femtometers and the negatively charged electrons revolve about the nucleus in a cloud, the radius of which is of the order of 1 Å [see Fig. 2.2(B)].
(b) Thomson model
The Thomson “plum pudding” model of the atom results in a Gaussian distribution of α particles about the incident pencil beam direction expressed as follows
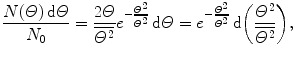
where
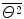
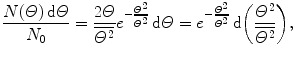
(2.8)
N 0
is the incident number of α particles, i.e., the number of α particles striking the gold foil.
Θ
is the scattering angle of the α particle after it passes through the gold foil.
N(Θ) dΘ
is the number of α particles scattered within the angular range of Θ and Θ+dΘ, i.e., scattered between angles Θ and Θ+dΘ.
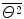
is the mean square net deflection experimentally determined to be of the order of 3×10−4 rad2 giving 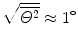 .
.
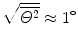 .
.(c) Rutherford model
The distribution of scattered α particles assuming the validity of the Rutherford nuclear model is given as follows
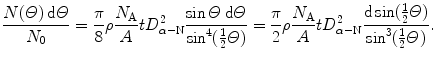
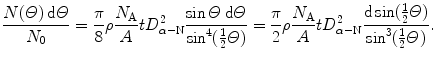
(2.9)
The distribution in (2.9) can be derived as follows. In general, the number N of scattering events is proportional to the incident particle beam intensity N 0 as well as to the number n of atoms (nuclei) per unit area. The proportionality constant is defined as the cross section σ for the scattering event and N is then expressed as
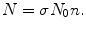
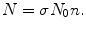
(2.10)
In (2.10) the absorber (scattering foil) is assumed to be thin enough to ensure that the incident particles have only one or no scattering events as they traverse the absorber. The probability of scattering into scattering angles from θ to θ+dθ is given by

where θ is the scattering angle in a single scattering event in contrast to Θ which is the combined scattering angle for α particle traversal of the gold foil, Ω is the solid angle, and dσ Ruth/dΩ is the Rutherford differential cross section given as (T2.38)
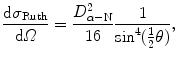
with D α−N the distance of closest approach in a direct hit (head-on) collision where θ=π.

(2.11)
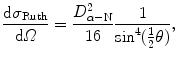
(2.12)
The number of atoms 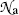 per area S of the absorber (scattering foil) is given as follows
per area S of the absorber (scattering foil) is given as follows
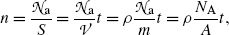
where t, 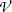 , m, and ρ are the thickness, volume, mass, and density, respectively, of the absorber foil; N A is the Avogadro number, and A is the atomic mass of the scattering foil.
, m, and ρ are the thickness, volume, mass, and density, respectively, of the absorber foil; N A is the Avogadro number, and A is the atomic mass of the scattering foil.
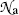 per area S of the absorber (scattering foil) is given as follows
per area S of the absorber (scattering foil) is given as follows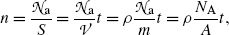
(2.13)
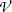 , m, and ρ are the thickness, volume, mass, and density, respectively, of the absorber foil; N A is the Avogadro number, and A is the atomic mass of the scattering foil.
, m, and ρ are the thickness, volume, mass, and density, respectively, of the absorber foil; N A is the Avogadro number, and A is the atomic mass of the scattering foil.The number of α particles scattered into an angular range of θ to θ+dθ normalized to the number of incident α particles N 0 is determined from (2.11) as follows
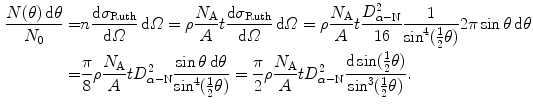
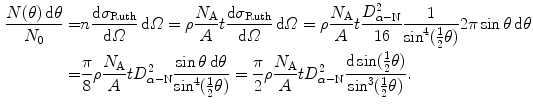
(2.14)
Since the vast majority of α particles experience only one Rutherford interaction while traversing the foil, the probability for multiple Rutherford interactions is very low and one can replace the single scattering angle θ in (2.14) with angle Θ to get the following distribution for α particles traversing the foil
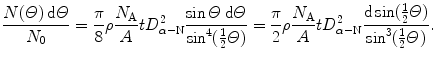
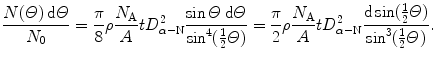
(2.15)
N(θ) dθ/N 0 can be considered the probability that incident particles will be scattered into the angular range from θ to θ+dθ corresponding to impact parameter range from b to b−db.
(d) In the early 20th century physicists had two competing models of the atom: (1) Thomson “plum pudding” model and (2) Rutherford nuclear model, each model predicting significantly different α-particle scattering probabilities from the other model. The Rutherford model eventually prevailed based on unequivocal support from experimental results and today the Rutherford model is considered the universally accepted model of the atom.
(1) According to the Thompson model of the atom the probability of an α particle to be scattered between angle Θ and Θ+dΘ is given by (2.8). To get the probability of an α particle to be scattered between angles Θ 1 and Θ 2 we integrate (2.8) and get
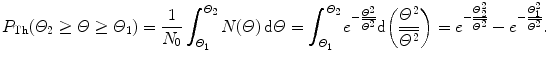
Inserting 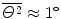 , Θ 1=10∘, and Θ 2=12∘ into (2.16), we get
, Θ 1=10∘, and Θ 2=12∘ into (2.16), we get
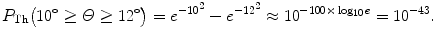
(2) The probability of an α particle to be scattered between angle Θ and Θ+dΘ according to the Rutherford nuclear model of the atom is given by (2.9). The probability of an α particle to be scattered between angle Θ 1 and Θ 2 according to Rutherford nuclear model of the atom is obtained by integrating (2.9) from Θ 1 to Θ 2 to get
![$$\begin{aligned} P_{\mathrm{Ruth}}(\varTheta _{2} \ge \varTheta \ge \varTheta _{1}) =& \frac{1}{N_{0}}\int_{\varTheta _{1}}^{\varTheta _{2}} N(\varTheta )\,\mathrm{d} \varTheta = \frac{\pi}{2}\rho \frac{N_{\mathrm{A}}}{A}t D_{\alpha - \mathrm{N}}^{2} \int_{\varTheta _{1}}^{\varTheta _{2}} \frac{\mathrm{d} \sin (\tfrac{1}{2}\varTheta )}{\sin ^{3}(\tfrac{1}{2}\varTheta )} \\ =& \frac{\pi}{4}\rho \frac{N_{\mathrm{A}}}{A}t D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{1}{\sin ^{2}(\frac{1}{2}\varTheta )} \biggr]_{\varTheta _{2}}^{\varTheta _{1}} \\ =& \frac{\pi}{4} \rho \frac{N_{\mathrm{A}}}{A}t D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{\sin ^{2}(\tfrac{1}{2}\varTheta _{2}) - \sin ^{2}(\frac{1}{2}\varTheta _{1})}{\sin ^{2}(\tfrac{1}{2}\varTheta _{1})\sin ^{2} (\frac{1}{2}\varTheta _{2})} \biggr]. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ18.gif)
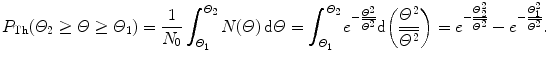
(2.16)
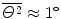 , Θ 1=10∘, and Θ 2=12∘ into (2.16), we get
, Θ 1=10∘, and Θ 2=12∘ into (2.16), we get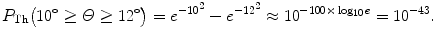
(2.17)
![$$\begin{aligned} P_{\mathrm{Ruth}}(\varTheta _{2} \ge \varTheta \ge \varTheta _{1}) =& \frac{1}{N_{0}}\int_{\varTheta _{1}}^{\varTheta _{2}} N(\varTheta )\,\mathrm{d} \varTheta = \frac{\pi}{2}\rho \frac{N_{\mathrm{A}}}{A}t D_{\alpha - \mathrm{N}}^{2} \int_{\varTheta _{1}}^{\varTheta _{2}} \frac{\mathrm{d} \sin (\tfrac{1}{2}\varTheta )}{\sin ^{3}(\tfrac{1}{2}\varTheta )} \\ =& \frac{\pi}{4}\rho \frac{N_{\mathrm{A}}}{A}t D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{1}{\sin ^{2}(\frac{1}{2}\varTheta )} \biggr]_{\varTheta _{2}}^{\varTheta _{1}} \\ =& \frac{\pi}{4} \rho \frac{N_{\mathrm{A}}}{A}t D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{\sin ^{2}(\tfrac{1}{2}\varTheta _{2}) - \sin ^{2}(\frac{1}{2}\varTheta _{1})}{\sin ^{2}(\tfrac{1}{2}\varTheta _{1})\sin ^{2} (\frac{1}{2}\varTheta _{2})} \biggr]. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ18.gif)
(2.18)
We now use (2.18) to determine the probability of an α particle to be scattered with scattering angle Θ between Θ 1=10∘ and Θ 2=12∘ but, before embarking on the calculation, we must determine the distance of closest approach D α−N for a head-on collision between a 5.4 MeV α particle and a gold nucleus (T2.12)
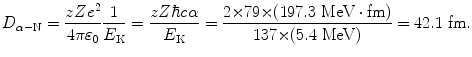
For a 2.5 μm thick gold foil, the probability of an α particle to be scattered between angles Θ 1=10∘ and Θ 2=12∘ is based on (2.19) given as follows
![$$\begin{aligned} &P_{\mathrm{Ruth}}\bigl(10^\circ \ge \varTheta \ge 12^\circ \bigr) \\ &\quad{}= \frac{\pi {\times} (19.3 {\times} 10^{6}\ \mathrm{g} \cdot \mathrm{m}^{ - 3}) {\times} (6.022 {\times} 10^{23}\ \mathrm{mol}^{ - 1}) {\times} (2.5 {\times} 10^{ - 6}\ \mathrm{m}) {\times} (42.1 {\times} 10^{ - 15}\ \mathrm{m})^{2}}{4 {\times} (197\ \mathrm{g} \cdot \mathrm{mol}^{ - 1})} \\ &\qquad{}{\times} \biggl[ \frac{\sin ^{2}(10^\circ ) - \sin ^{2}(12^\circ )}{\sin ^{2}(10^\circ ) {\times} \sin ^{2}(12^\circ )} \biggr] \\ &\quad{}= 8.2 {\times} 10^{ - 3}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ20.gif)
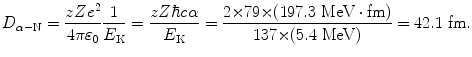
(2.19)
![$$\begin{aligned} &P_{\mathrm{Ruth}}\bigl(10^\circ \ge \varTheta \ge 12^\circ \bigr) \\ &\quad{}= \frac{\pi {\times} (19.3 {\times} 10^{6}\ \mathrm{g} \cdot \mathrm{m}^{ - 3}) {\times} (6.022 {\times} 10^{23}\ \mathrm{mol}^{ - 1}) {\times} (2.5 {\times} 10^{ - 6}\ \mathrm{m}) {\times} (42.1 {\times} 10^{ - 15}\ \mathrm{m})^{2}}{4 {\times} (197\ \mathrm{g} \cdot \mathrm{mol}^{ - 1})} \\ &\qquad{}{\times} \biggl[ \frac{\sin ^{2}(10^\circ ) - \sin ^{2}(12^\circ )}{\sin ^{2}(10^\circ ) {\times} \sin ^{2}(12^\circ )} \biggr] \\ &\quad{}= 8.2 {\times} 10^{ - 3}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ20.gif)
(2.20)
Comparing (2.17) and (2.20), the probability of an α particle to be scattered between angle Θ 1=10∘ and Θ 2=12∘ according to the Rutherford nuclear model of the atom is substantially greater than that predicted by the Thomson model of the atom. Extensive experimental work has confirmed the validity of the Rutherford nuclear model of the atom in comparison with the Thomson model of the atom.
2.2.Q2 (64)
Using the general results of Prob. 63 for Rutherford scattering on the Thomson and Rutherford models of the atom, determine, for the Geiger-Marsden experiment with α particles of kinetic energy E K striking a gold foil of thickness t, the fractional number of α particles scattered with angle Θ 0 or larger assuming the validity of:
(a)
Thomson “plum pudding” model.
(b)
Thomson “plum pudding” model and t=1 μm and 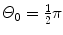 .
.
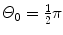 .
.(c)
Rutherford nuclear model.
(d)
Rutherford nuclear model and t=1 μm, 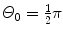 , and E K=5.5 MeV.
, and E K=5.5 MeV.
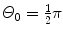 , and E K=5.5 MeV.
, and E K=5.5 MeV.SOLUTION:
(a) In conjunction with the Thomson model the number of α particles scattered by a foil of thickness t with an angle equal to or larger than Θ 0 is from (2.8) given as
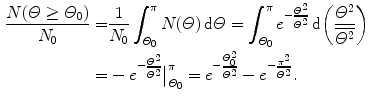
(b) For the Thomson model the number of α particles scattered by a foil of thickness t of 1 μm with an angle equal to or larger than 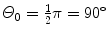 is from (2.21) given as
is from (2.21) given as
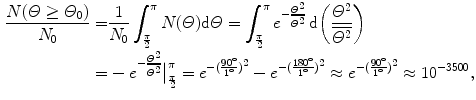
where we used the experimentally determined value of ∼1∘ for the root mean square angle 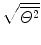 .
.
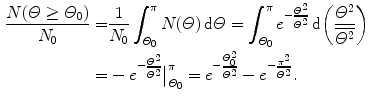
(2.21)
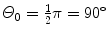 is from (2.21) given as
is from (2.21) given as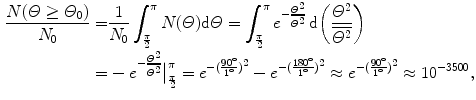
(2.22)
 .
.(c) In conjunction with the Rutherford model of the atom the number of α particles scattered by a foil of thickness t with an angle equal to or larger than Θ 0 is from (2.15) given as
![$$\begin{aligned} \frac{N(\varTheta \ge \varTheta _{0})}{N_{0}} =& \frac{1}{N_{0}}\int_{\varTheta _{0}}^{\pi} N(\varTheta )\,\mathrm{d}\varTheta = \frac{\pi}{2}\rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2} \int_{\varTheta _{0}}^{\pi} \frac{\mathrm{d}\sin (\frac{1}{2}\varTheta )}{\sin ^{3}(\frac{1}{2}\varTheta )} \\ =& - \frac{\pi}{4}\rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{1}{\sin ^{2}(\frac{1}{2}\varTheta )} \biggr]_{\varTheta _{0}}^{\pi} \\ =& \frac{\pi}{4} \rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{1}{\sin ^{2}(\frac{1}{2}\varTheta _{0})} - 1 \biggr] \\ =& \frac{\pi}{4}\rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2}\cot ^{2}\biggl(\frac{1}{2}\varTheta _{0}\biggr) = C(A,t)\cot ^{2}\biggl(\frac{1}{2}\varTheta _{0}\biggr), \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ23.gif)
where C(A,t) is a constant depending on the atomic mass A and thickness t of the target. For a given target material and thickness the fractional number of α particles scattered with a scattering angle exceeding Θ 0 increases rapidly with decreasing Θ 0, as shown in Fig. 2.3.
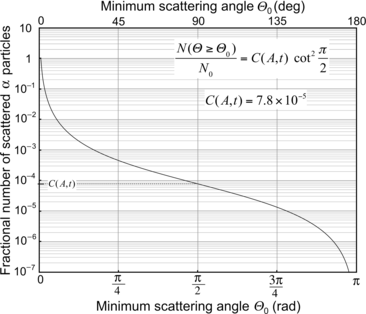
![$$\begin{aligned} \frac{N(\varTheta \ge \varTheta _{0})}{N_{0}} =& \frac{1}{N_{0}}\int_{\varTheta _{0}}^{\pi} N(\varTheta )\,\mathrm{d}\varTheta = \frac{\pi}{2}\rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2} \int_{\varTheta _{0}}^{\pi} \frac{\mathrm{d}\sin (\frac{1}{2}\varTheta )}{\sin ^{3}(\frac{1}{2}\varTheta )} \\ =& - \frac{\pi}{4}\rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{1}{\sin ^{2}(\frac{1}{2}\varTheta )} \biggr]_{\varTheta _{0}}^{\pi} \\ =& \frac{\pi}{4} \rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2} \biggl[ \frac{1}{\sin ^{2}(\frac{1}{2}\varTheta _{0})} - 1 \biggr] \\ =& \frac{\pi}{4}\rho t\frac{N_{\mathrm{A}}}{A}D_{\alpha - \mathrm{N}}^{2}\cot ^{2}\biggl(\frac{1}{2}\varTheta _{0}\biggr) = C(A,t)\cot ^{2}\biggl(\frac{1}{2}\varTheta _{0}\biggr), \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ23.gif)
(2.23)

Fig. 2.3
Fractional number of scattered α particles against the minimum scattering angle θ 0 for α particles scattered on gold nucleus
(d) For the Rutherford atomic model, the fractional number of α particles scattered by a gold scattering foil of thickness t=1 μm with a scattering angle Θ equal to 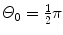 or larger is calculated from (2.23) after inserting appropriate values for the pertinent parameters: ρ Au=19.3 g/cm−3; A=197 g/mol; N A=6.022×1023 mol−1; and D α−N=41 fm. The value of 41.4 fm for D α−N is obtained from Prob. 62 which plots D α−N, the distance of closest approach in a head-on α particle collision with a gold nucleus, against kinetic energy E K of α particles. With these values the fraction
or larger is calculated from (2.23) after inserting appropriate values for the pertinent parameters: ρ Au=19.3 g/cm−3; A=197 g/mol; N A=6.022×1023 mol−1; and D α−N=41 fm. The value of 41.4 fm for D α−N is obtained from Prob. 62 which plots D α−N, the distance of closest approach in a head-on α particle collision with a gold nucleus, against kinetic energy E K of α particles. With these values the fraction 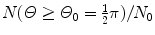 is given as
is given as
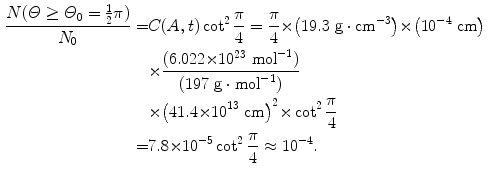
This result, stating a probability of about 10−4 for scattering of α particles with an angle larger than 90∘ on 1 μm thick gold foil, confirms the validity of the Rutherford model of the atom. Moreover, it agrees very well with experimental results that Geiger and Marsden obtained in their historic experiment which showed that roughly one in 104 α particles was scattered with scattering angles larger than 90∘. While relatively small, this probability is nonetheless enormous compared to the probability 10−3500 calculated with the Thomson model in (b).
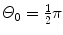 or larger is calculated from (2.23) after inserting appropriate values for the pertinent parameters: ρ Au=19.3 g/cm−3; A=197 g/mol; N A=6.022×1023 mol−1; and D α−N=41 fm. The value of 41.4 fm for D α−N is obtained from Prob. 62 which plots D α−N, the distance of closest approach in a head-on α particle collision with a gold nucleus, against kinetic energy E K of α particles. With these values the fraction
or larger is calculated from (2.23) after inserting appropriate values for the pertinent parameters: ρ Au=19.3 g/cm−3; A=197 g/mol; N A=6.022×1023 mol−1; and D α−N=41 fm. The value of 41.4 fm for D α−N is obtained from Prob. 62 which plots D α−N, the distance of closest approach in a head-on α particle collision with a gold nucleus, against kinetic energy E K of α particles. With these values the fraction 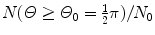 is given as
is given as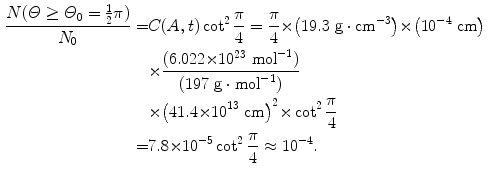
(2.24)
2.3 Rutherford Scattering
2.3.Q1 (65)
Many approaches have been developed for the derivation of the Rutherford α-particle scattering formula. The fastest and most elegant approach is based on the derivation of the momentum transfer Δp from the α particle to the nucleus.
(a)
Plot a schematic diagram of the α particle scattering on a gold nucleus and clearly label all parameters that play a role in the scattering process.
(b)
Derive the relationship between the impact parameter b and the scattering angle θ using the momentum transfer Δp approach.
(c)
Show that the impact parameter b that is usually expressed as
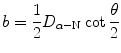
can also be expressed as
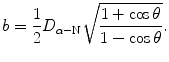
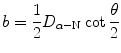
(2.25)
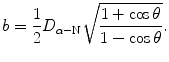
(2.26)
SOLUTION:
(a) The schematic diagram of the scattering process is presented in Fig. 2.4. The nucleus of mass M and atomic number Z is in the outer focus of the hyperbola because of the repulsive interaction between the α particle and the nucleus and the assumption is made that M≫m α with m α the mass of the α particle. The other parameters of Fig. 2.4 are defined as follows:
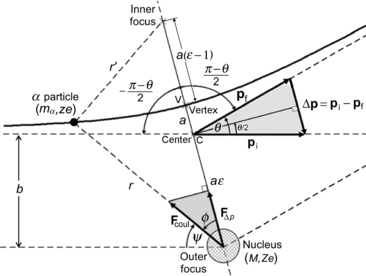
r
is the distance between the α particle and the nucleus (outer focus).
r′
is the distance between the α particle and the inner focus.
a
is the distance between the vertex V and the center C of the hyperbola.
b
is the impact parameter.
ε
is the eccentricity of the hyperbola.
θ
is the scattering angle.
F Coul
is the Coulomb force between the α particle and the nucleus.
F Δp
is the projection of F Coul onto the axis of symmetry of the hyperbola.

Fig. 2.4
Schematic diagram of α particle scattering
(b) The relationship between the impact parameter b and the scattering angle θ is derived as follows:
The momentum transfer Δp from the α particle to the nucleus can be treated as an impulse that is equal to the change in momentum of the α particle and defined as the integral of force F with respect to time t. As shown in Fig. 2.3, the momentum transfer is along a line that bisects the angle π−θ. The magnitude of the Coulomb force acting on the α particle is given by
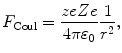
where
The component of the Coulomb force F Coul in the direction of the momentum transfer is F Δp =F Coulcosϕ so that the momentum transfer (impulse) Δp can be written as the time integral of the force component F Δp
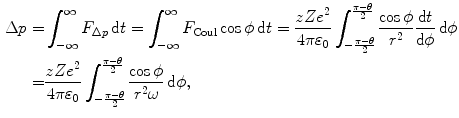
where
We now use the conservation of angular momentum L for the α-scattering process to obtain a relationship between the angular frequency ω and impact parameter b. For the α particle at a very large distance (r=∞) from the nucleus, L is given as L=m α υ i b with m α and υ i the mass and initial velocity of the α particle. For the α particle in the vertex of the hyperbolic trajectory, on the other hand, we get L=m α ωr 2. Thus
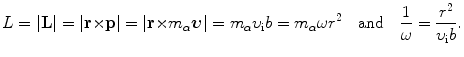
Inserting (2.29) into (2.28) the momentum transfer is now expressed as
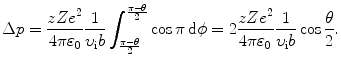
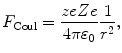
(2.27)
r
is the distance between the α particle and the nucleus of mass M, atomic number Z, and atomic mass number A.
z
is the atomic number of the α particle.
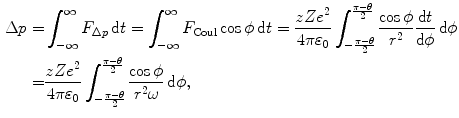
(2.28)
ϕ
is the angle between the radius vector r and the bisector.
dt/dϕ
is the inverse of the angular frequency ω.
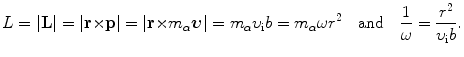
(2.29)
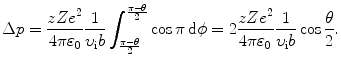
(2.30)
The momentum vector diagram of Fig. 2.4 shows that Δp can also be expressed as follows
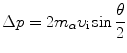
and this expression combined with (2.30) results in the following relationship between the impact parameter b and scattering angle θ
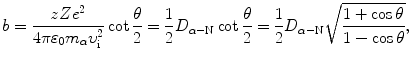
where D α−N is the distance of closest approach in a direct-hit collision between an α particle and the nucleus (T2.12).
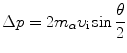
(2.31)
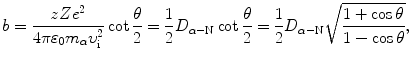
(2.32)
(c) We show that
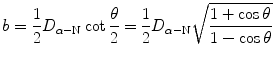
by recalling the well known trigonometric expression 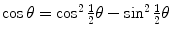 in conjunction with the following trigonometric identity
in conjunction with the following trigonometric identity 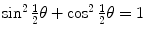 to get
to get
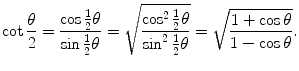
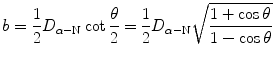
(2.33)
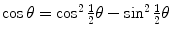 in conjunction with the following trigonometric identity
in conjunction with the following trigonometric identity 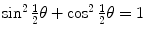 to get
to get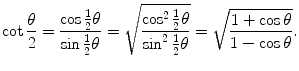
(2.34)
2.3.Q2 (66)
A lithium ion Li+++ (Z=3, A=6 g/mol) with incident kinetic energy (E K)i=7.5 MeV is scattered on a gold nucleus (Z=79, A=197 g/mol) through an angle θ of 10∘. Assume that the mass of the alpha particle is much smaller than the mass of the lithium ion and calculate:
(a)
Impact parameter b.
(b)
Distance of closest approach R α−N.
(c)
Eccentricity of the hyperbolic trajectory of the Li+++ ion.
(d)
Distance a between the vertex V and the center C of the hyperbolic trajectory.
SOLUTION:
Before calculating the individual parameters of the specific scattering interaction, we calculate the distance of closest approach in a head-on elastic collision between the Li+++ ion and gold nucleus using (T2.12)
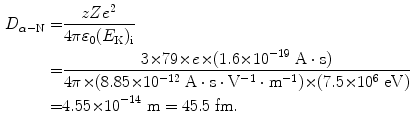
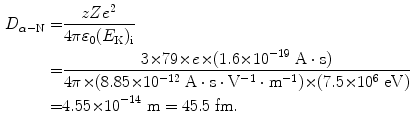
(2.35)
(a)
Impact parameter b is calculated from (T2.23) as
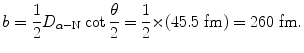
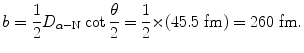
(2.36)
(b)
Distance of closest approach is calculated from (T2.31) as follows
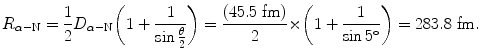
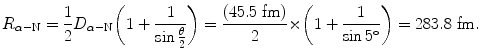
(2.37)
(c)
Eccentricity ε of the trajectory is calculated from (T2.28) as follows
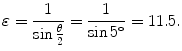
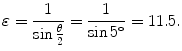
(2.38)
(d)
Distance a between the vertex V and the center C of the hyperbolic trajectory is calculated using (T2.30)
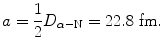
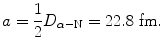
(2.39)
2.3.Q3 (67)
An α particle interacts with a silver nucleus (atomic number Z=47, atomic mass A=108, and rest mass Mc 2=100455 MeV) and undergoes Rutherford scattering with scattering angle θ of 45∘ resulting in a distance of closest approach R α−N of 32.2 fm. For this Rutherford scattering event:
(a)
Calculate impact parameter b.
(b)
Calculate kinetic energy E K of the incident α particle.
(c)
Calculate momentum p α of the incident α particle.
(d)
Calculate recoil momentum Δp of the nucleus.
(e)
Calculate recoil energy ΔE K of the nucleus.
(f)
Calculate eccentricity ε of the hyperbolic trajectory of the α particle.
(g)
Draw a schematic diagram of the scattering event and clearly show all given and calculated parameters.
SOLUTION:
(a) The impact parameter b is calculated using (T2.31) to get
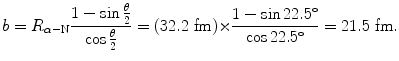
(b) Kinetic energy E K of the incident α particle is calculated using (T2.12) which contains D α−N, the distance of closest approach in a head-on collision (θ=π, b=0), calculated using (T2.23) as follows
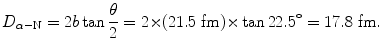
According to (T2.12) E K is given as follows
![$$\begin{aligned} E_{\mathrm{K}} =& \frac{2zZe^{2}}{4\pi \varepsilon _{0}}\frac{1}{D_{\alpha - \mathrm{N}}} = \frac{2 {\times} 47 {\times} (1.602 {\times} 10^{ - 19}\ \mathrm{A} \cdot \mathrm{s}) {\times} e}{4\pi {\times} [8.85 {\times} 10^{ - 12}\ \mathrm{A} \cdot \mathrm{s}/(\mathrm{V} \cdot \mathrm{m})] {\times} (17.8 {\times} 10^{ - 15}\ \mathrm{m})} \\ =& 7.6\ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ42.gif)
(c) Momentum of the incident α particle is calculated using the standard p vs E K relativistic expression given in (T1.64) as follows
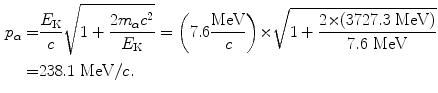
(d) Recoil momentum Δp of the nucleus is calculated using (T2.22) to get
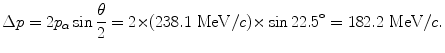
(e) Recoil energy ΔE K of the nucleus is determined from the standard relativistic equation for kinetic energy as follows
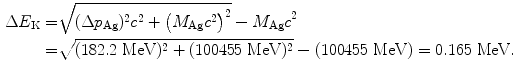
(f) Eccentricity ε of the α particle trajectory is determined from (T2.28) to get
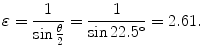
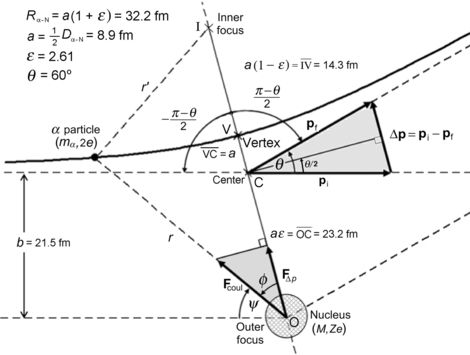
(g) Schematic diagram of the scattering process is shown in Fig. 2.5.
(2.40)
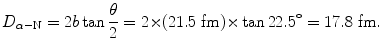
(2.41)
![$$\begin{aligned} E_{\mathrm{K}} =& \frac{2zZe^{2}}{4\pi \varepsilon _{0}}\frac{1}{D_{\alpha - \mathrm{N}}} = \frac{2 {\times} 47 {\times} (1.602 {\times} 10^{ - 19}\ \mathrm{A} \cdot \mathrm{s}) {\times} e}{4\pi {\times} [8.85 {\times} 10^{ - 12}\ \mathrm{A} \cdot \mathrm{s}/(\mathrm{V} \cdot \mathrm{m})] {\times} (17.8 {\times} 10^{ - 15}\ \mathrm{m})} \\ =& 7.6\ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_2_Chapter_Equ42.gif)
(2.42)
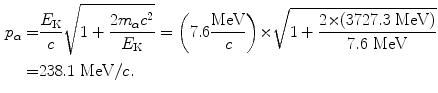
(2.43)
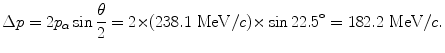
(2.44)
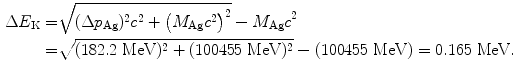
(2.45)
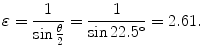
(2.46)

Fig. 2.5
Schematic diagram of the Rutherford scattering process with scattering angle θ=45∘ and the distance of closest approach R α−N=32.2 fm defined as the distance between the outer focus and vertex of the hyperbolic trajectory
2.3.Q4 (68)
An α particle with initial kinetic energy (E K)i of 5.5 MeV and initial velocity υ i undergoes a direct-hit Rutherford scattering (head-on collision) on a gold nucleus.
(a)
Derive and plot the general relationship for υ x /υ i against x/D α−N for the α particle with x the α particle distance from the center of the nucleus, υ x the velocity of the α particle at x, and D α−N the distance of closest approach in a direct-hit collision of the α particle with the nucleus.
(b)
Calculate the initial velocity of the 5.5 MeV α particle.
(c)
Determine υ x /υ i of the α particle when the particle is a distance x=2D α−N from the nucleus. For a 5.5 MeV α particle D α−N was determined as 41.3 fm in Prob. 62.
(d)
Calculate the distance x at which the α particle velocity υ x is at 50 % of its initial velocity υ i.
(e)
Calculate the distance x at which the α particle velocity υ x is at 90 % of its initial velocity υ i.
SOLUTION:
(a) In a direct-hit elastic collision between an α particle and a nucleus (scattering angle θ=π and impact parameter b=0) the following expression holds in general for the conservation of energy of the α particle.
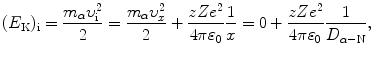
where
Equation (2.47) states that at any point x of the α particle trajectory the total α particle energy which is the sum of kinetic energy 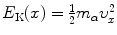 and potential energy E P(x)=zZe 2/(4πε 0 x) is equal to initial kinetic energy (E K)i of the α particle. We thus have
and potential energy E P(x)=zZe 2/(4πε 0 x) is equal to initial kinetic energy (E K)i of the α particle. We thus have
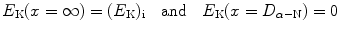
as well as
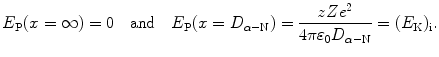
To derive a general expression for normalized velocity υ x /υ i as a function of normalized distance x/D α−N we insert (2.49) into (2.47) and get
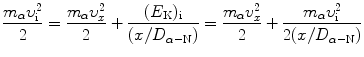
Solving (2.50) for υ x /υ i gives the following result
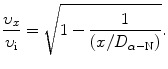
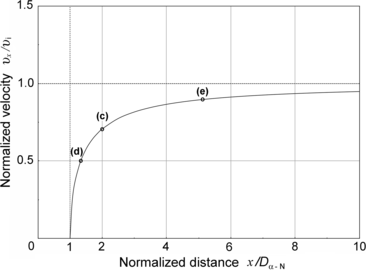
A plot of normalized velocity υ x /υ i against the normalized distance x/D α−N is given in Fig. 2.6. The plot is valid for all classical α particles irrespective of the kinetic energy of the α particle. Points (c), (d), and (e) on the graph represent solutions for problem sections (c), (d), and (e) below.
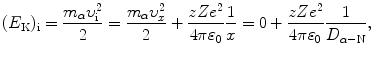
(2.47)
x
is the distance between the α particle and the nucleus in a direct-hit collision
υ i
is the initial velocity of the α particle (at x=∞).
(E K)i
is the initial kinetic energy of the α particle (at x=∞).
E K(x)
is the kinetic energy at x.
E P(x)
is the potential energy at x.
D α−N
is the distance of closest approach in a direct-hit collision (θ=π) between the α particle and the nucleus.
υ x
is the velocity of the α particle at a distance x from the nucleus for D α−N≤x≤∞.
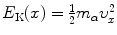 and potential energy E P(x)=zZe 2/(4πε 0 x) is equal to initial kinetic energy (E K)i of the α particle. We thus have
and potential energy E P(x)=zZe 2/(4πε 0 x) is equal to initial kinetic energy (E K)i of the α particle. We thus have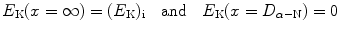
(2.48)
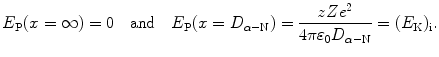
(2.49)
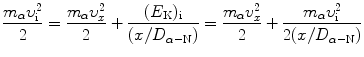
(2.50)
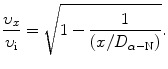
(2.51)

Fig. 2.6
Normalized velocity υ x /υ i against normalized distance x/D α−N for classical direct-hit α particle Rutherford scattering. Points labeled (c), (d), and (e) correspond to results obtained in sections (c), (d), and (e)
(b) Velocity of 5.5 MeV α particle is calculated in (T2.5) classically and in (T2.7) relativistically as follows
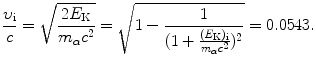
The first square-root in (2.52) follows from the classical expression for kinetic energy while the second comes from relativistic considerations. Both give the same result, since the initial kinetic energy of the α particle is much smaller than its rest energy, allowing us to use the classical expression for E K(x) in (2.47).
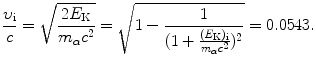
(2.52)
(c) Our specific problem calls for determination of the ratio υ x /υ i for x=2D α−N. Inserting x/D α−N=2 into (2.51) we obtain the following result
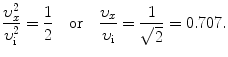
(d) To calculate the distance at which the α particle velocity υ x is 50 % of its initial velocity υ i we use (2.51) and solve for x/D α−N to get
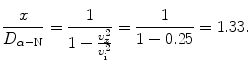
(e) To calculate the distance at which the α particle velocity υ x is 90 % of its initial velocity υ i we use (2.54) and get
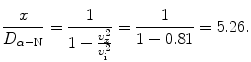
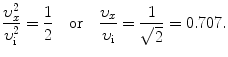
(2.53)
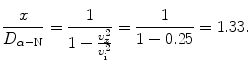
(2.54)
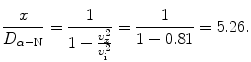
(2.55)
2.3.Q5 (69)
A hyperbola consists of two disconnected open curves called the arms or branches of the hyperbola. The distance of closest approach between the two branches defines the vertices of the hyperbola, one vertex V for each branch. A straight line through the two vertices defines the transverse axis of the hyperbola, and the midpoint between the two vertices on the transverse axis is the center C of the hyperbola.
Show that the two expressions [(T2.27) and (T2.32), respectively]
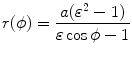
and
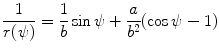
given in polar coordinates for the trajectory of an α particle undergoing Rutherford elastic scattering on a high atomic number nucleus are equivalent. The trajectory is a hyperbola and the polar coordinate system is centered at the outer focus FO




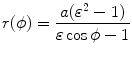
(2.56)
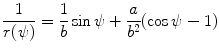
(2.57)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree