(1)
of an object by minimization of an energy functional that consists of an external energy
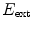 attracting the contour to image features and an internal energy
attracting the contour to image features and an internal energy 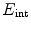 that enforces smoothness of the contour. The energy functional may, for instance, be given by
that enforces smoothness of the contour. The energy functional may, for instance, be given by![$$\begin{aligned} E[ \varvec{x}] = -\int _{s=0}^1\parallel \varvec{\nabla }I(\varvec{x}(s))\parallel ^2 ds + \alpha \int _{s = 0}^1\parallel \partial ^2 / \partial s^2 \varvec{x}(s) \parallel ^2 ds \text {.} \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_Equ2.gif)
(2)
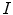 with high gradients and the weight
with high gradients and the weight 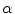 controls smoothness of the contour. This approach has been extremely successful and a huge number of papers were published proposing variations of energy terms and applying it to numerous problems. The approach was also applied in medical image analysis and extended for the segmentation of surfaces in 3D images [5, 6].
controls smoothness of the contour. This approach has been extremely successful and a huge number of papers were published proposing variations of energy terms and applying it to numerous problems. The approach was also applied in medical image analysis and extended for the segmentation of surfaces in 3D images [5, 6].Active shape models [2] are another very successful approach. The approach relies on establishing a number 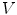 of corresponding points
of corresponding points 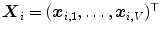 on a set of
on a set of 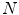 reference objects (
reference objects (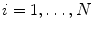 ) of the same kind. After aligning the objects, a point-distribution model (PDM)
) of the same kind. After aligning the objects, a point-distribution model (PDM)
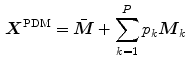
is constructed via principal component analysis (PCA), i.e. the mean shape
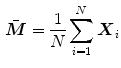
is computed and modes 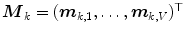 describing shape variations are derived from the
describing shape variations are derived from the 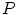 largest eigenvectors of the matrix
largest eigenvectors of the matrix
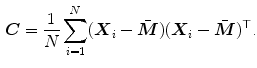
Assuming that an initial model position and shape is given, adaptation of the PDM is done by detecting borders along normals of the object boundary and modifying the parameters 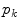 of the PDM to minimize the distance to the detected border points. Also for this approach numerous variants have been introduced and the basic approach was applied to a large number of problems. In particular, the approach was extended for 3D medical image segmentation [7].
of the PDM to minimize the distance to the detected border points. Also for this approach numerous variants have been introduced and the basic approach was applied to a large number of problems. In particular, the approach was extended for 3D medical image segmentation [7].
 of corresponding points
of corresponding points 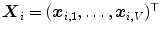 on a set of
on a set of 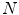 reference objects (
reference objects (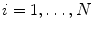 ) of the same kind. After aligning the objects, a point-distribution model (PDM)
) of the same kind. After aligning the objects, a point-distribution model (PDM)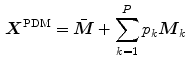
(3)
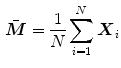
(4)
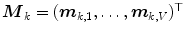 describing shape variations are derived from the
describing shape variations are derived from the  largest eigenvectors of the matrix
largest eigenvectors of the matrix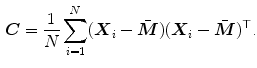
(5)
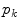 of the PDM to minimize the distance to the detected border points. Also for this approach numerous variants have been introduced and the basic approach was applied to a large number of problems. In particular, the approach was extended for 3D medical image segmentation [7].
of the PDM to minimize the distance to the detected border points. Also for this approach numerous variants have been introduced and the basic approach was applied to a large number of problems. In particular, the approach was extended for 3D medical image segmentation [7].When segmenting an anatomical object like a bone or the heart with a stable topology between different individuals, active shape models differ in two important aspects from active contour models. First, the segmentation accuracy of active shape models is limited by the number of eigenvectors and the training samples used to construct them while active contour models can in principle approximate any (smooth) shape. Of course, the flexibility of active shape models may be increased by adding more eigenvectors and artificially generating additional reference shapes, but the advantage of a compact model with a few parameters will be lost. Second, by establishing corresponding points, the points of an active shape model can, at least approximately, be associated with an anatomical location, while active contour models do not allow this. This property is very important as it allows to attach individual boundary detectors to each point and enables segmentation of organs with different boundary properties for different parts.
2.2 Shape Constrained Deformable Models
SCDMs [1] have been introduced to combine the advantages of active contour models with those of active shape models. In particular, they have been designed to allow for an accurate approximation of anatomical objects, while each point of the model can be associated with an anatomical region.
In the following we consider the segmentation of anatomical objects in 3D medical images. The deformable model is represented by a mesh with 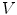 vertices
vertices 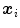 and
and 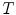 triangles with centers
triangles with centers 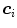 . Adaptation of the mesh to an image is done by iterating a boundary detection step and a mesh deformation step. Boundary detection is done by detecting points
. Adaptation of the mesh to an image is done by iterating a boundary detection step and a mesh deformation step. Boundary detection is done by detecting points 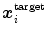 with high gradient along profiles parallel to the mesh normal (see also Sect. 4). Mesh deformation is done by minimizing an energy
with high gradient along profiles parallel to the mesh normal (see also Sect. 4). Mesh deformation is done by minimizing an energy
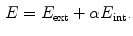
The external energy 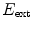 drives the mesh towards the detected borders
drives the mesh towards the detected borders
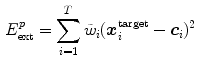
or the associated surfaces
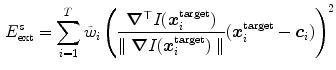
with weights 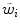 derived from the boundary detection step. The internal energy
derived from the boundary detection step. The internal energy
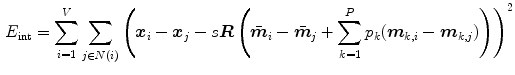
compares the difference vectors between two neighboring mesh vertices of the deforming model and the shape model. 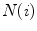 denotes the neighbors of vertex
denotes the neighbors of vertex 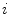 . The scaling parameter
. The scaling parameter 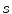 and the rotation matrix
and the rotation matrix 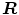 allow to properly align both models. Finally, it should be mentioned that in addition to the mesh vertices, the modes
allow to properly align both models. Finally, it should be mentioned that in addition to the mesh vertices, the modes 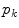 of the shape model, the scaling parameter
of the shape model, the scaling parameter 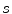 , and the rotation matrix
, and the rotation matrix 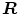 are optimized in the mesh deformation step.
are optimized in the mesh deformation step.
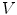 vertices
vertices 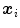 and
and 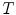 triangles with centers
triangles with centers 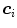 . Adaptation of the mesh to an image is done by iterating a boundary detection step and a mesh deformation step. Boundary detection is done by detecting points
. Adaptation of the mesh to an image is done by iterating a boundary detection step and a mesh deformation step. Boundary detection is done by detecting points 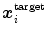 with high gradient along profiles parallel to the mesh normal (see also Sect. 4). Mesh deformation is done by minimizing an energy
with high gradient along profiles parallel to the mesh normal (see also Sect. 4). Mesh deformation is done by minimizing an energy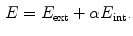
(6)
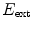 drives the mesh towards the detected borders
drives the mesh towards the detected borders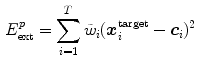
(7)
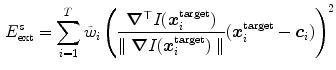
(8)
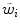 derived from the boundary detection step. The internal energy
derived from the boundary detection step. The internal energy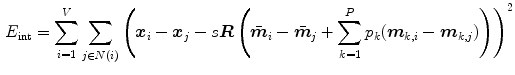
(9)
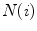 denotes the neighbors of vertex
denotes the neighbors of vertex 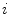 . The scaling parameter
. The scaling parameter 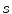 and the rotation matrix
and the rotation matrix 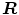 allow to properly align both models. Finally, it should be mentioned that in addition to the mesh vertices, the modes
allow to properly align both models. Finally, it should be mentioned that in addition to the mesh vertices, the modes 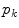 of the shape model, the scaling parameter
of the shape model, the scaling parameter 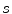 , and the rotation matrix
, and the rotation matrix 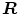 are optimized in the mesh deformation step.
are optimized in the mesh deformation step.The internal energy of a SCDM does essentially embed a shape model into a deformable model and introduces regularization by penalizing deviations from the shape model instead of imposing a smoothness constraint. In addition, the approach approximately maintains the distribution of mesh vertices as given by the shape model. This mechanism preserves the property of shape models that each point can be associated with an anatomical location.
2.3 Example Results for Vertebra Segmentation
For illustration, segmentation results for 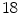 vertebra in
vertebra in 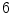 CT images generated with a SCDM with
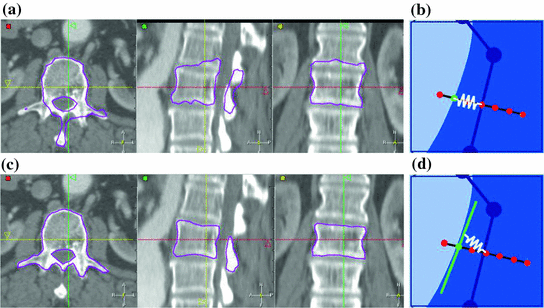
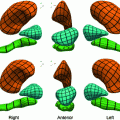
CT images generated with a SCDM with 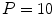 modes are briefly discussed [1]. For initialization, the mean vertebra model has been placed with an Euclidean surface-to-surface error of 2.5–3.5 mm compared to the reference segmentation. Model adaptation resulted in an average error of 1.3 mm when attracting the model directly to the detected boundaries (Eq. 7), and in 0.9 mm when attracting the model to the associated surfaces (Eq. 8). Fig. 1 shows an exemplary result.
modes are briefly discussed [1]. For initialization, the mean vertebra model has been placed with an Euclidean surface-to-surface error of 2.5–3.5 mm compared to the reference segmentation. Model adaptation resulted in an average error of 1.3 mm when attracting the model directly to the detected boundaries (Eq. 7), and in 0.9 mm when attracting the model to the associated surfaces (Eq. 8). Fig. 1 shows an exemplary result.
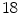 vertebra in
vertebra in 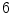 CT images generated with a SCDM with
CT images generated with a SCDM with 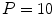 modes are briefly discussed [1]. For initialization, the mean vertebra model has been placed with an Euclidean surface-to-surface error of 2.5–3.5 mm compared to the reference segmentation. Model adaptation resulted in an average error of 1.3 mm when attracting the model directly to the detected boundaries (Eq. 7), and in 0.9 mm when attracting the model to the associated surfaces (Eq. 8). Fig. 1 shows an exemplary result.
modes are briefly discussed [1]. For initialization, the mean vertebra model has been placed with an Euclidean surface-to-surface error of 2.5–3.5 mm compared to the reference segmentation. Model adaptation resulted in an average error of 1.3 mm when attracting the model directly to the detected boundaries (Eq. 7), and in 0.9 mm when attracting the model to the associated surfaces (Eq. 8). Fig. 1 shows an exemplary result.The example shows that the basic idea of SCDMs works. In addition, it demonstrates the importance of the external energy and whether the model is directly attracted towards the detected boundary points or to the associated surfaces. Though the difference between the corresponding average segmentation errors of 1.3 and 0.9 mm is only 0.4 mm, the segmentation result looks unacceptable in the former case, while a good segmentation result is obtained in the latter case. This impression can potentially be explained by large segmentation errors in some regions while an accurate segmentation is obtained in other regions, and shows that comparatively small differences in surface-to-surface metrics can make a relevant difference.
3 Shape Variability
Robust and accurate model adaptation relies on a suitable shape parameterization. We first summarize results related to PCA-based shape models where SCDMs have been used to establish corresponding points. Afterwards we introduce multi-linear models as an alternative approach to parameterize shape variability. The latter approach is exploited in the SCDM framework as it offers an intuitive way to parameterize shape variability that leads to good shape approximations and can easily be generalized to complex models.
3.1 PCA-Based Shape Models
Construction of an active shape model requires to establish 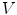 corresponding points
corresponding points 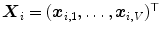 on a set of
on a set of 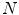 reference objects of the same kind. Looking at the surface of a 3D organ, this is a non-trivial task, because there is usually no dense set of anatomical landmarks that can unambiguously be identified. A number of methods has been proposed to address this task. They can be classified into mesh-to-mesh, mesh-to-volume and volume-to-volume registration [7].
reference objects of the same kind. Looking at the surface of a 3D organ, this is a non-trivial task, because there is usually no dense set of anatomical landmarks that can unambiguously be identified. A number of methods has been proposed to address this task. They can be classified into mesh-to-mesh, mesh-to-volume and volume-to-volume registration [7].
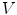 corresponding points
corresponding points 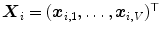 on a set of
on a set of 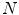 reference objects of the same kind. Looking at the surface of a 3D organ, this is a non-trivial task, because there is usually no dense set of anatomical landmarks that can unambiguously be identified. A number of methods has been proposed to address this task. They can be classified into mesh-to-mesh, mesh-to-volume and volume-to-volume registration [7].
reference objects of the same kind. Looking at the surface of a 3D organ, this is a non-trivial task, because there is usually no dense set of anatomical landmarks that can unambiguously be identified. A number of methods has been proposed to address this task. They can be classified into mesh-to-mesh, mesh-to-volume and volume-to-volume registration [7].SCDMs have been designed in a way that each point can be associated with an anatomical location. They can therefore be used for establishing corresponding points. Starting with a set of 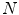 binary images representing the different instances of the anatomical structure-of-interest, an arbitrarily selected instance can be used as reference to derive a mesh model by triangulation. This mesh model is then subsequently adapted to the remaining
binary images representing the different instances of the anatomical structure-of-interest, an arbitrarily selected instance can be used as reference to derive a mesh model by triangulation. This mesh model is then subsequently adapted to the remaining 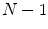 binary images. This approach belongs to the mesh-to-volume category and has been used to construct shape models of vertebrae and femurs [8].
binary images. This approach belongs to the mesh-to-volume category and has been used to construct shape models of vertebrae and femurs [8].
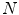 binary images representing the different instances of the anatomical structure-of-interest, an arbitrarily selected instance can be used as reference to derive a mesh model by triangulation. This mesh model is then subsequently adapted to the remaining
binary images representing the different instances of the anatomical structure-of-interest, an arbitrarily selected instance can be used as reference to derive a mesh model by triangulation. This mesh model is then subsequently adapted to the remaining 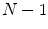 binary images. This approach belongs to the mesh-to-volume category and has been used to construct shape models of vertebrae and femurs [8].
binary images. This approach belongs to the mesh-to-volume category and has been used to construct shape models of vertebrae and femurs [8].The results for 32 vertebrae (L1–L4) derived from CT scans with an in-plane resolution of 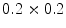 mm
mm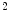 to
to 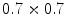 mm
mm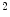 and a slice thickness between 2 and 3 mm show that the reference mesh can be adapted to the binary images representing the other vertebrae with an average surface-to-surface error of 0.8 mm. The accuracy of corresponding anatomical positions has been assessed using the tips of the processes as landmarks. They have been encoded in the reference mesh by marking the corresponding triangle. After adapting the reference mesh to the binary image of another instance, these triangle positions have been compared with the manually defined landmarks resulting in an average Euclidean distance of 2.1 mm. This result provides evidence for the statement that points of a SCDM can approximately be associated with an anatomical location, especially when keeping in mind that the result is also affected by the accuracy of manual landmark definition.
and a slice thickness between 2 and 3 mm show that the reference mesh can be adapted to the binary images representing the other vertebrae with an average surface-to-surface error of 0.8 mm. The accuracy of corresponding anatomical positions has been assessed using the tips of the processes as landmarks. They have been encoded in the reference mesh by marking the corresponding triangle. After adapting the reference mesh to the binary image of another instance, these triangle positions have been compared with the manually defined landmarks resulting in an average Euclidean distance of 2.1 mm. This result provides evidence for the statement that points of a SCDM can approximately be associated with an anatomical location, especially when keeping in mind that the result is also affected by the accuracy of manual landmark definition.
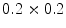 mm
mm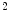 to
to 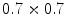 mm
mm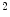 and a slice thickness between 2 and 3 mm show that the reference mesh can be adapted to the binary images representing the other vertebrae with an average surface-to-surface error of 0.8 mm. The accuracy of corresponding anatomical positions has been assessed using the tips of the processes as landmarks. They have been encoded in the reference mesh by marking the corresponding triangle. After adapting the reference mesh to the binary image of another instance, these triangle positions have been compared with the manually defined landmarks resulting in an average Euclidean distance of 2.1 mm. This result provides evidence for the statement that points of a SCDM can approximately be associated with an anatomical location, especially when keeping in mind that the result is also affected by the accuracy of manual landmark definition.
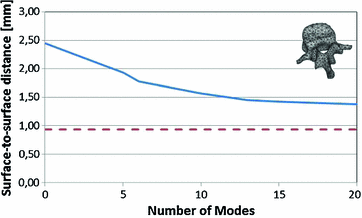
and a slice thickness between 2 and 3 mm show that the reference mesh can be adapted to the binary images representing the other vertebrae with an average surface-to-surface error of 0.8 mm. The accuracy of corresponding anatomical positions has been assessed using the tips of the processes as landmarks. They have been encoded in the reference mesh by marking the corresponding triangle. After adapting the reference mesh to the binary image of another instance, these triangle positions have been compared with the manually defined landmarks resulting in an average Euclidean distance of 2.1 mm. This result provides evidence for the statement that points of a SCDM can approximately be associated with an anatomical location, especially when keeping in mind that the result is also affected by the accuracy of manual landmark definition.Generalizability of the PCA-based shape models has been addressed by leave-one-out experiments where a PDM was built from all vertebrae but one and adapted to the left out vertebra. Figure 2 shows the resulting surface-to-surface error in dependence of the number of modes  . The results show that the approximation accuracy increases with the number of modes
. The results show that the approximation accuracy increases with the number of modes  . The benefit of additional modes decreases, however, and the approximation accuracy is only marginally improved when using more modes than
. The benefit of additional modes decreases, however, and the approximation accuracy is only marginally improved when using more modes than 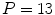 . The resulting approximation accuracy of 1.4 mm is clearly worse than the 0.9 mm obtained with SCDM segmentation [1]. Although care must be taken in the comparison since metric and test set are not identical, the results show that SCDMs relax shape constraints and can, therefore, lead to more accurate results than active shape models.
. The resulting approximation accuracy of 1.4 mm is clearly worse than the 0.9 mm obtained with SCDM segmentation [1]. Although care must be taken in the comparison since metric and test set are not identical, the results show that SCDMs relax shape constraints and can, therefore, lead to more accurate results than active shape models.
 . The results show that the approximation accuracy increases with the number of modes
. The results show that the approximation accuracy increases with the number of modes  . The benefit of additional modes decreases, however, and the approximation accuracy is only marginally improved when using more modes than
. The benefit of additional modes decreases, however, and the approximation accuracy is only marginally improved when using more modes than 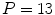 . The resulting approximation accuracy of 1.4 mm is clearly worse than the 0.9 mm obtained with SCDM segmentation [1]. Although care must be taken in the comparison since metric and test set are not identical, the results show that SCDMs relax shape constraints and can, therefore, lead to more accurate results than active shape models.
. The resulting approximation accuracy of 1.4 mm is clearly worse than the 0.9 mm obtained with SCDM segmentation [1]. Although care must be taken in the comparison since metric and test set are not identical, the results show that SCDMs relax shape constraints and can, therefore, lead to more accurate results than active shape models.
Fig. 3
Approximation of an unseen heart with a PCA-based shape model [9]. The dashed line corresponds to shape approximation with a multi-linear model
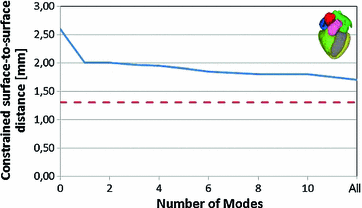
A similar experiment was performed for a 4-chamber heart model [9]. In this work, 28 cardiac CTA images from 13 patients corresponding to different heart phases with an in-plane resolution of 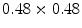 mm
mm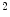 and a slice thickness between 0.67 and 3 mm were used. Corresponding meshes and ground truth annotations have been generated simultaneously in a bootstrap approach using SCDMs, and the resulting meshes have been used to build PCA-based shape models. Generalizability has been addressed by leave-one-patient-out experiments to avoid that results are biased by the shape of a patient’s heart. Figure 3 shows the mean constrained surface-to-surface error, which is close to a surface-to-surface error but avoids meaningless comparisons of non-corresponding mesh parts. The approximation accuracy increases with the number of modes, but the curve becomes flat and usage of more than
and a slice thickness between 0.67 and 3 mm were used. Corresponding meshes and ground truth annotations have been generated simultaneously in a bootstrap approach using SCDMs, and the resulting meshes have been used to build PCA-based shape models. Generalizability has been addressed by leave-one-patient-out experiments to avoid that results are biased by the shape of a patient’s heart. Figure 3 shows the mean constrained surface-to-surface error, which is close to a surface-to-surface error but avoids meaningless comparisons of non-corresponding mesh parts. The approximation accuracy increases with the number of modes, but the curve becomes flat and usage of more than 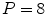 modes leads only to marginal improvements.
modes leads only to marginal improvements.
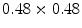 mm
mm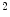 and a slice thickness between 0.67 and 3 mm were used. Corresponding meshes and ground truth annotations have been generated simultaneously in a bootstrap approach using SCDMs, and the resulting meshes have been used to build PCA-based shape models. Generalizability has been addressed by leave-one-patient-out experiments to avoid that results are biased by the shape of a patient’s heart. Figure 3 shows the mean constrained surface-to-surface error, which is close to a surface-to-surface error but avoids meaningless comparisons of non-corresponding mesh parts. The approximation accuracy increases with the number of modes, but the curve becomes flat and usage of more than
and a slice thickness between 0.67 and 3 mm were used. Corresponding meshes and ground truth annotations have been generated simultaneously in a bootstrap approach using SCDMs, and the resulting meshes have been used to build PCA-based shape models. Generalizability has been addressed by leave-one-patient-out experiments to avoid that results are biased by the shape of a patient’s heart. Figure 3 shows the mean constrained surface-to-surface error, which is close to a surface-to-surface error but avoids meaningless comparisons of non-corresponding mesh parts. The approximation accuracy increases with the number of modes, but the curve becomes flat and usage of more than 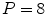 modes leads only to marginal improvements.
modes leads only to marginal improvements.Both examples illustrate that shape models with a few modes derived by principal component analysis allow to approximate anatomical structures with a surprisingly high accuracy. Though other approaches for establishing correspondences than SCDMs may lead to better results, approaches that further increase the flexibility of shape models and allow for a more accurate approximation are desired.
3.2 Multi-Linear Models
One class of approaches to increase model flexibility is to subdivide an anatomical structure into several parts and model their shape variability independently [7, 10–12]. One particular approach [9, 13] consists in partitioning an anatomical object in 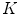 parts and modeling the variability of part
parts and modeling the variability of part 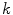 by a linear transformation
by a linear transformation ![$${\fancyscript{T}}_{k}({\mathbf {q}}_{k})[.]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq46.gif) where
where 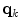 describes the transformation parameters. With this approach, the mean model can be transformed according to
describes the transformation parameters. With this approach, the mean model can be transformed according to
![$$\begin{aligned} {\fancyscript{T}}_{\text {multi-linear}}({\mathbf {q}})[\bar{\varvec{m}}_i] = \sum _{k=1}^{K} w_{i,k} \cdot {\fancyscript{T}}_k({\mathbf {q}}_k)[\bar{\varvec{m}}_i] \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_Equ10.gif)
If all parts would be independent, the subdivision can be described by weights
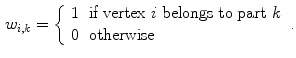
To avoid discontinuities between the individual parts, the transformations are interpolated in transition regions that depend on the geodesic distance to the border between the parts. Practically, this is done by assigning weights 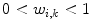 with
with 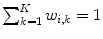 in transition regions.
in transition regions.
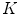 parts and modeling the variability of part
parts and modeling the variability of part 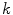 by a linear transformation
by a linear transformation ![$${\fancyscript{T}}_{k}({\mathbf {q}}_{k})[.]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq46.gif) where
where 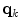 describes the transformation parameters. With this approach, the mean model can be transformed according to
describes the transformation parameters. With this approach, the mean model can be transformed according to![$$\begin{aligned} {\fancyscript{T}}_{\text {multi-linear}}({\mathbf {q}})[\bar{\varvec{m}}_i] = \sum _{k=1}^{K} w_{i,k} \cdot {\fancyscript{T}}_k({\mathbf {q}}_k)[\bar{\varvec{m}}_i] \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_Equ10.gif)
(10)
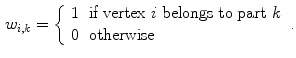
(11)
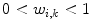 with
with 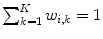 in transition regions.
in transition regions.This approach has been used to parameterize the shape of a 4-chamber heart model [9]. In particular, affine transformations (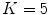 ) have been assigned to the left atrium, the right atrium, the left ventricular epicardium, the left ventricular endocardium (together with the aortic trunk) and the right ventricle (together with the pulmonary artery). The capability to approximate an unknown shape has been assessed in the same way and using the same data as it has been done for the PCA-based shape model of Fig. 3. Therein, the resulting mean constrained surface-to-surface error is shown by the dashed red line.
) have been assigned to the left atrium, the right atrium, the left ventricular epicardium, the left ventricular endocardium (together with the aortic trunk) and the right ventricle (together with the pulmonary artery). The capability to approximate an unknown shape has been assessed in the same way and using the same data as it has been done for the PCA-based shape model of Fig. 3. Therein, the resulting mean constrained surface-to-surface error is shown by the dashed red line.
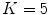 ) have been assigned to the left atrium, the right atrium, the left ventricular epicardium, the left ventricular endocardium (together with the aortic trunk) and the right ventricle (together with the pulmonary artery). The capability to approximate an unknown shape has been assessed in the same way and using the same data as it has been done for the PCA-based shape model of Fig. 3. Therein, the resulting mean constrained surface-to-surface error is shown by the dashed red line.
) have been assigned to the left atrium, the right atrium, the left ventricular epicardium, the left ventricular endocardium (together with the aortic trunk) and the right ventricle (together with the pulmonary artery). The capability to approximate an unknown shape has been assessed in the same way and using the same data as it has been done for the PCA-based shape model of Fig. 3. Therein, the resulting mean constrained surface-to-surface error is shown by the dashed red line.The result shows that this intuitive way of parameterizing shape leads to a better approximation. Though the multi-linear model has more parameters (60 resulting from 5 affine transformations with 12 parameters) than the PCA-based shape model (37 corresponding to 25 modes and an affine transformation describing pose), there is no indication that global PCA-analysis would lead to a more compact model that approximates unknown shapes with similar or better accuracy. In addition, local modeling of shape variability via partitioning allows to describe shape variability of complex anatomical structures and organs within a single framework. A multi-linear model has, for instance, been used to construct a shape parameterization of the heart with the major vessels [14]. Shape variability of the vessels was modeled by assigning similarity transformations to vessel segments (Fig. 4).
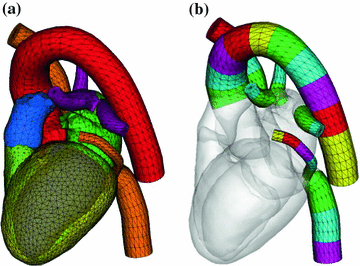

Fig. 4
Heart model [14] with large vessels (a). For multi-linear shape modeling, the vessels are subdivided into segments (b)
Modeling of shape variability by multi-linear transformations can easily be included in the SCDM framework. For that purpose, the internal energy of Eq. (9) is replaced by
![$$\begin{aligned} E_\mathrm{int} = \sum _{i=1}^{V} \sum _{j \in N(i)} \sum _{k=1}^{K} w_{i,k} \left( \varvec{x}_{i} - \varvec{x}_{j} - \left( {\fancyscript{T}}_k({\mathbf {q}}_k)[\bar{\varvec{m}}_i] - {\fancyscript{T}}_k({\mathbf {q}}_k)[\bar{\varvec{m}}_j] \right) \right) ^2 \text {.} \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_Equ12.gif)
The parameters 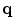 of the multi-linear transformation are optimized in addition to the vertex positions
of the multi-linear transformation are optimized in addition to the vertex positions 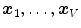 during mesh deformation by energy minimization.
during mesh deformation by energy minimization.
![$$\begin{aligned} E_\mathrm{int} = \sum _{i=1}^{V} \sum _{j \in N(i)} \sum _{k=1}^{K} w_{i,k} \left( \varvec{x}_{i} - \varvec{x}_{j} - \left( {\fancyscript{T}}_k({\mathbf {q}}_k)[\bar{\varvec{m}}_i] - {\fancyscript{T}}_k({\mathbf {q}}_k)[\bar{\varvec{m}}_j] \right) \right) ^2 \text {.} \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_Equ12.gif)
(12)
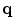 of the multi-linear transformation are optimized in addition to the vertex positions
of the multi-linear transformation are optimized in addition to the vertex positions 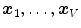 during mesh deformation by energy minimization.
during mesh deformation by energy minimization.4 Boundary Detection Framework
A key problem when adapting a surface model to medical images is the abundance of misleading structures that need to be distinguished from the wanted organ surfaces. In addition, boundary characteristics may vary over the organ surface. The boundary detection framework is therefore of key importance for robust and accurate adaptation of a SCDM to images. We first describe how boundaries are detected and the type of features that we use. Specific boundary detection functions are generated via the analysis of training images. “Simulated Search” is used to select the best boundary detection function per triangle. Finally, we summarize some results that have been generated in the context of heart segmentation.
4.1 Boundary Detection
As explained in Sect. 2.2, adaptation of the mesh to an image is done by iterating a boundary detection step and a mesh deformation step that minimizes the energy 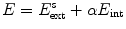 (see Eqs. (6)–(9)). Similar as for active shape models [2, 7], boundary detection is done by searching for each mesh triangle a characteristic point along profiles parallel to the mesh normals.
(see Eqs. (6)–(9)). Similar as for active shape models [2, 7], boundary detection is done by searching for each mesh triangle a characteristic point along profiles parallel to the mesh normals.
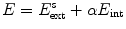 (see Eqs. (6)–(9)). Similar as for active shape models [2, 7], boundary detection is done by searching for each mesh triangle a characteristic point along profiles parallel to the mesh normals.
(see Eqs. (6)–(9)). Similar as for active shape models [2, 7], boundary detection is done by searching for each mesh triangle a characteristic point along profiles parallel to the mesh normals.Formally, for triangle 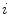 , we establish a search profile
, we establish a search profile 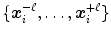 centered at the triangle center
centered at the triangle center 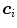 . The profile is oriented along the triangle normal with equidistantly spaced points
. The profile is oriented along the triangle normal with equidistantly spaced points 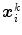 . Among these profile points, a target point is detected:
. Among these profile points, a target point is detected:
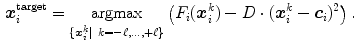
Here, 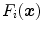 is a triangle-specific function with a large positive response for surface points (e.g., the local gradient magnitude
is a triangle-specific function with a large positive response for surface points (e.g., the local gradient magnitude 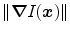 ). The distance penalty with weighting factor
). The distance penalty with weighting factor 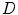 allows to bias the search to nearby target points. The feature response together with the distance penalty is also used to define the weight
allows to bias the search to nearby target points. The feature response together with the distance penalty is also used to define the weight
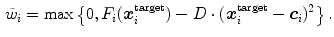
of the detected boundary point in the external energy of Eqs. (7) and (8).
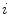 , we establish a search profile
, we establish a search profile 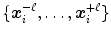 centered at the triangle center
centered at the triangle center 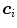 . The profile is oriented along the triangle normal with equidistantly spaced points
. The profile is oriented along the triangle normal with equidistantly spaced points 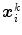 . Among these profile points, a target point is detected:
. Among these profile points, a target point is detected: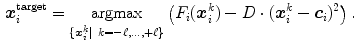
(13)
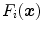 is a triangle-specific function with a large positive response for surface points (e.g., the local gradient magnitude
is a triangle-specific function with a large positive response for surface points (e.g., the local gradient magnitude 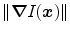 ). The distance penalty with weighting factor
). The distance penalty with weighting factor 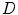 allows to bias the search to nearby target points. The feature response together with the distance penalty is also used to define the weight
allows to bias the search to nearby target points. The feature response together with the distance penalty is also used to define the weight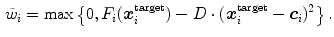
(14)
4.2 Features
Organ boundaries in medical images are often associated with intensity transitions. The image gradient 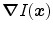 builds, therefore, the basis of the features
builds, therefore, the basis of the features 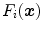 that we use. The image gradient is projected onto the triangle normal
that we use. The image gradient is projected onto the triangle normal 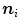 to suppress edges that deviate strongly from the local surface orientation. To control the maximum feature response for structures like metal implants in CT images, we use a heuristic damping of gradients exceeding a threshold
to suppress edges that deviate strongly from the local surface orientation. To control the maximum feature response for structures like metal implants in CT images, we use a heuristic damping of gradients exceeding a threshold 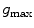 [1]:
[1]:
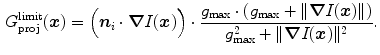
This quantity builds together with the sign 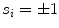 the basis of our features
the basis of our features
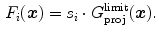
The sign indicates per triangle 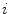 whether the boundary is expected to show a bright-to-dark transition or vice versa.
whether the boundary is expected to show a bright-to-dark transition or vice versa.
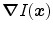 builds, therefore, the basis of the features
builds, therefore, the basis of the features 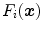 that we use. The image gradient is projected onto the triangle normal
that we use. The image gradient is projected onto the triangle normal 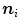 to suppress edges that deviate strongly from the local surface orientation. To control the maximum feature response for structures like metal implants in CT images, we use a heuristic damping of gradients exceeding a threshold
to suppress edges that deviate strongly from the local surface orientation. To control the maximum feature response for structures like metal implants in CT images, we use a heuristic damping of gradients exceeding a threshold 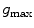 [1]:
[1]: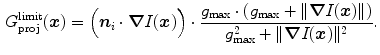
(15)
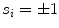 the basis of our features
the basis of our features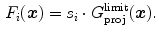
(16)
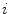 whether the boundary is expected to show a bright-to-dark transition or vice versa.
whether the boundary is expected to show a bright-to-dark transition or vice versa.Such a simple feature leads to many positive responses, and a large number of unwanted boundary points are typically detected. Local gray values and gradient sizes [15–19] have been used to design more specific features and to improve discrimination from false boundaries. We use a general formulation and constrain the admissible edges by a set 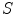 of local image criteria
of local image criteria 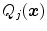
![$$\begin{aligned} F_i(\varvec{x}) = \left\{ \begin{array}{ll} s_i\cdot {G_\mathrm{proj}^\mathrm{limit}}(\varvec{x}) &{} \text {if } Q_j(\varvec{x})\!\in \![\text {Min}_{i,j}, \text {Max}_{i,j}]\ \forall \,j\!\in \! S,\\ 0 &{} \text {otherwise}. \end{array} \right. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_Equ17.gif)
If any of the criteria’s value is not within its triangle-specific acceptance interval ![$$[\text {Min}_{i,j}, \text {Max}_{i,j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq69.gif) , the associated boundary is rejected by setting its response to 0.
, the associated boundary is rejected by setting its response to 0.
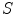 of local image criteria
of local image criteria 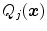
![$$\begin{aligned} F_i(\varvec{x}) = \left\{ \begin{array}{ll} s_i\cdot {G_\mathrm{proj}^\mathrm{limit}}(\varvec{x}) &{} \text {if } Q_j(\varvec{x})\!\in \![\text {Min}_{i,j}, \text {Max}_{i,j}]\ \forall \,j\!\in \! S,\\ 0 &{} \text {otherwise}. \end{array} \right. \end{aligned}$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_Equ17.gif)
(17)
![$$[\text {Min}_{i,j}, \text {Max}_{i,j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq69.gif) , the associated boundary is rejected by setting its response to 0.
, the associated boundary is rejected by setting its response to 0.Typically, we use criteria 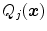 such as local gray values on either side of the surface, averaged over several points perpendicular or parallel to the surface, and changes of gray values across the surface. The latter can be characterized by first or second order Taylor coefficients of a local gray value profile or simply by the difference of inside versus outside gray values. If needed, these criteria can be extended to better capture local characteristics and to improve discrimination. If, for instance, the gray-value transition (bright-to-dark or vice versa) is less predictable, the signed gradient
such as local gray values on either side of the surface, averaged over several points perpendicular or parallel to the surface, and changes of gray values across the surface. The latter can be characterized by first or second order Taylor coefficients of a local gray value profile or simply by the difference of inside versus outside gray values. If needed, these criteria can be extended to better capture local characteristics and to improve discrimination. If, for instance, the gray-value transition (bright-to-dark or vice versa) is less predictable, the signed gradient 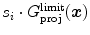 may be replaced by its absolute value
may be replaced by its absolute value 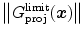 . Furthermore, gray-value normalization may be introduced to allow application of the features for imaging modalities without calibrated gray-scale (see Sect. 5.3).
. Furthermore, gray-value normalization may be introduced to allow application of the features for imaging modalities without calibrated gray-scale (see Sect. 5.3).
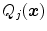 such as local gray values on either side of the surface, averaged over several points perpendicular or parallel to the surface, and changes of gray values across the surface. The latter can be characterized by first or second order Taylor coefficients of a local gray value profile or simply by the difference of inside versus outside gray values. If needed, these criteria can be extended to better capture local characteristics and to improve discrimination. If, for instance, the gray-value transition (bright-to-dark or vice versa) is less predictable, the signed gradient
such as local gray values on either side of the surface, averaged over several points perpendicular or parallel to the surface, and changes of gray values across the surface. The latter can be characterized by first or second order Taylor coefficients of a local gray value profile or simply by the difference of inside versus outside gray values. If needed, these criteria can be extended to better capture local characteristics and to improve discrimination. If, for instance, the gray-value transition (bright-to-dark or vice versa) is less predictable, the signed gradient 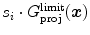 may be replaced by its absolute value
may be replaced by its absolute value 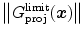 . Furthermore, gray-value normalization may be introduced to allow application of the features for imaging modalities without calibrated gray-scale (see Sect. 5.3).
. Furthermore, gray-value normalization may be introduced to allow application of the features for imaging modalities without calibrated gray-scale (see Sect. 5.3).4.3 Feature Parameterization
The feature functions of Eq. (17) depend on several parameters such as the sign 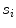 of the expected gradient orientation and the acceptance intervals
of the expected gradient orientation and the acceptance intervals ![$$[\text {Min}_{i,j}, \text {Max}_{i,j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq74.gif) per triangle. In the simplest case, the same feature function may be used for all triangles. Its parameters can be derived from a statistical analysis of the parameter values on a collection of training images with reference meshes. This analysis takes the positions
per triangle. In the simplest case, the same feature function may be used for all triangles. Its parameters can be derived from a statistical analysis of the parameter values on a collection of training images with reference meshes. This analysis takes the positions 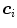 of the triangles of a reference mesh per image and evaluates
of the triangles of a reference mesh per image and evaluates 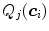 . Based on these values, we can define acceptance intervals
. Based on these values, we can define acceptance intervals ![$$[\text {Min}_{j}, \text {Max}_{j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq77.gif) that extend, for instance, from a lower to an upper percentile value of the observed values of the criteria
that extend, for instance, from a lower to an upper percentile value of the observed values of the criteria 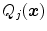 .
.
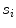 of the expected gradient orientation and the acceptance intervals
of the expected gradient orientation and the acceptance intervals ![$$[\text {Min}_{i,j}, \text {Max}_{i,j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq74.gif) per triangle. In the simplest case, the same feature function may be used for all triangles. Its parameters can be derived from a statistical analysis of the parameter values on a collection of training images with reference meshes. This analysis takes the positions
per triangle. In the simplest case, the same feature function may be used for all triangles. Its parameters can be derived from a statistical analysis of the parameter values on a collection of training images with reference meshes. This analysis takes the positions 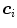 of the triangles of a reference mesh per image and evaluates
of the triangles of a reference mesh per image and evaluates 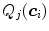 . Based on these values, we can define acceptance intervals
. Based on these values, we can define acceptance intervals ![$$[\text {Min}_{j}, \text {Max}_{j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq77.gif) that extend, for instance, from a lower to an upper percentile value of the observed values of the criteria
that extend, for instance, from a lower to an upper percentile value of the observed values of the criteria 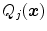 .
.To account for variations of the image appearance across the organ surface, the global statistical analysis can be preceded by a clustering procedure that groups the mesh triangles into clusters of similar appearance (see, e.g., [18, 20–22]). This can be done using 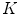 -means clustering based on the vector of criteria
-means clustering based on the vector of criteria 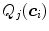 . The statistical analysis is then performed per cluster of mesh triangles, resulting in acceptance intervals
. The statistical analysis is then performed per cluster of mesh triangles, resulting in acceptance intervals ![$$[\text {Min}_{k,j}, \text {Max}_{k,j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq81.gif) for each cluster
for each cluster 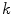 . The sign
. The sign 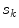 can also be adjusted per triangle cluster. With this clustering-based approach, all triangles of a cluster share the same parameterized feature function.
can also be adjusted per triangle cluster. With this clustering-based approach, all triangles of a cluster share the same parameterized feature function.
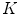 -means clustering based on the vector of criteria
-means clustering based on the vector of criteria 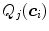 . The statistical analysis is then performed per cluster of mesh triangles, resulting in acceptance intervals
. The statistical analysis is then performed per cluster of mesh triangles, resulting in acceptance intervals ![$$[\text {Min}_{k,j}, \text {Max}_{k,j}]$$](/wp-content/uploads/2016/10/A312883_1_En_5_Chapter_IEq81.gif) for each cluster
for each cluster 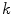 . The sign
. The sign 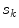 can also be adjusted per triangle cluster. With this clustering-based approach, all triangles of a cluster share the same parameterized feature function.
can also be adjusted per triangle cluster. With this clustering-based approach, all triangles of a cluster share the same parameterized feature function.Definition of the feature functions depends on various parameters and decisions. E.g., we can include or discard the gradient sign in Eq. (17). We can also use different sets of criteria 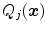 to constrain boundary detection and change the width of the acceptance intervals. These modifications will improve boundary detection for some triangles and deteriorate boundary detection for other triangles. For that reason, adaptation of a SCDM to images can be further improved by an approach that selects the optimal feature function for a triangle from a large number of feature function candidates, while the feature functions of Eq. (17) together with the clustering approach are very suited for generating a large number of good parametrized feature function candidates.
to constrain boundary detection and change the width of the acceptance intervals. These modifications will improve boundary detection for some triangles and deteriorate boundary detection for other triangles. For that reason, adaptation of a SCDM to images can be further improved by an approach that selects the optimal feature function for a triangle from a large number of feature function candidates, while the feature functions of Eq. (17) together with the clustering approach are very suited for generating a large number of good parametrized feature function candidates.
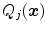 to constrain boundary detection and change the width of the acceptance intervals. These modifications will improve boundary detection for some triangles and deteriorate boundary detection for other triangles. For that reason, adaptation of a SCDM to images can be further improved by an approach that selects the optimal feature function for a triangle from a large number of feature function candidates, while the feature functions of Eq. (17) together with the clustering approach are very suited for generating a large number of good parametrized feature function candidates.
to constrain boundary detection and change the width of the acceptance intervals. These modifications will improve boundary detection for some triangles and deteriorate boundary detection for other triangles. For that reason, adaptation of a SCDM to images can be further improved by an approach that selects the optimal feature function for a triangle from a large number of feature function candidates, while the feature functions of Eq. (17) together with the clustering approach are very suited for generating a large number of good parametrized feature function candidates.4.4 “Simulated Search”
“Simulated Search” [23, 24] is an approach to rate the boundary detection performance of a feature function for a given triangle on the basis of training images and corresponding reference meshes. Starting with a set of feature function candidates, it is therefore possible to select the best performing feature function per mesh triangle and assign an optimal feature function 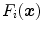 to each triangle
to each triangle 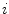 .
.
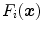 to each triangle
to each triangle 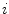 .
.The key idea of “Simulated Search” is to simulate boundary detection for an individual triangle as illustrated in Fig. 5. By shifting the position 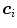 of a triangle as given by the reference mesh in a pre-defined neighborhood, we construct a pool of simulated search profiles. Also, the orientations of the search profiles may be varied to cover a certain range around the reference triangle’s normal direction. We then perform boundary detection according to Eq. (13) for a feature function out of the set of candidates and record for each simulated search profile the geometric distance between the detected target point
of a triangle as given by the reference mesh in a pre-defined neighborhood, we construct a pool of simulated search profiles. Also, the orientations of the search profiles may be varied to cover a certain range around the reference triangle’s normal direction. We then perform boundary detection according to Eq. (13) for a feature function out of the set of candidates and record for each simulated search profile the geometric distance between the detected target point 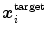 and the reference plane as defined by the normal of the reference triangle. This procedure is performed for all reference meshes. Finally, we compute the root-mean-square (RMS) error from all geometric distances that have been recorded for a specific triangle and a specific feature function, and assign the feature function candidate with the smallest average RMS error as feature function
and the reference plane as defined by the normal of the reference triangle. This procedure is performed for all reference meshes. Finally, we compute the root-mean-square (RMS) error from all geometric distances that have been recorded for a specific triangle and a specific feature function, and assign the feature function candidate with the smallest average RMS error as feature function 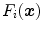 to triangle
to triangle 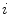 .
.
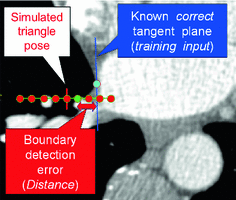
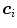 of a triangle as given by the reference mesh in a pre-defined neighborhood, we construct a pool of simulated search profiles. Also, the orientations of the search profiles may be varied to cover a certain range around the reference triangle’s normal direction. We then perform boundary detection according to Eq. (13) for a feature function out of the set of candidates and record for each simulated search profile the geometric distance between the detected target point
of a triangle as given by the reference mesh in a pre-defined neighborhood, we construct a pool of simulated search profiles. Also, the orientations of the search profiles may be varied to cover a certain range around the reference triangle’s normal direction. We then perform boundary detection according to Eq. (13) for a feature function out of the set of candidates and record for each simulated search profile the geometric distance between the detected target point 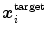 and the reference plane as defined by the normal of the reference triangle. This procedure is performed for all reference meshes. Finally, we compute the root-mean-square (RMS) error from all geometric distances that have been recorded for a specific triangle and a specific feature function, and assign the feature function candidate with the smallest average RMS error as feature function
and the reference plane as defined by the normal of the reference triangle. This procedure is performed for all reference meshes. Finally, we compute the root-mean-square (RMS) error from all geometric distances that have been recorded for a specific triangle and a specific feature function, and assign the feature function candidate with the smallest average RMS error as feature function 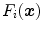 to triangle
to triangle 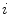 .
.
Fig. 5




Sketch illustrating the basic idea of “Simulated Search”. Along the simulated search profile (red points), the green target point is detected and its distance to the reference plane is determined
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree