computed tomography (CT) images of the lumbar spine. The resulting mean symmetric absolute surface distance of 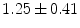 mm and Dice coefficient of
mm and Dice coefficient of 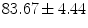 %, computed from the final vertebra detection results against corresponding reference vertebra segmentations, indicate that the proposed framework can successfully detected vertebrae in CT images of the lumbar spine.
%, computed from the final vertebra detection results against corresponding reference vertebra segmentations, indicate that the proposed framework can successfully detected vertebrae in CT images of the lumbar spine.
1 Introduction
Detection and segmentation of an object of interest can always be represented as a specific optimization problem. As optimization problems are usually non-deterministic polynomial-time hard (NP-hard) or non-analytically defined, they can be solved by brute force algorithms that are computationally demanding or by heuristic approaches that may not find the globally optimal solution. Moreover, if the optimization problem is ill-posed, there is no guarantee that the optimal detection or segmentation result is associated with the global optimum of the problem. Such lack of correspondence is observed in the case of vertebra detection in medical images of the spine, where neighboring vertebrae are of similar appearance and shape, which often causes mis-detections. We can therefore conclude that there is a need for an optimizer that will consider not only the global optimum but also local optima of the problem that represent candidate locations for each vertebra, and that can be further used for accurate and robust spine and vertebra detection. As standard optimization techniques, such as the Powell’s optimizer [1] or covariance matrix adaptation evolution strategy (CMA-ES) [2], detect only a single local optimum, we propose to use interpolation theory to overcome the above mentioned limitations and ensure the detection of all local optima. Interpolation theory estimates the behavior of smooth functions according to a small set of points, for which the behavior is known. In the case of object detection, interpolation theory can predict the position of the object of interest by computing a specified detector response for a sparse set of points, i.e. possible transformations of the object of interest. In this paper, we describe a novel framework for automated spine and vertebra detection in three-dimensional (3D) computed tomography (CT) images of the lumbar spine, where we first apply interpolation-based optimization to detect the location of the whole lumbar spine in the 3D image, and then detect the location of individual lumbar vertebrae within the spinal column.
2 Methodology
Detection of the object of interest (e.g. spine, vertebra) in an unknown 3D image 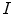 can be, in general, performed by optimizing an objective function
can be, in general, performed by optimizing an objective function 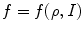 , which maps the model of the object of interest, represented by a set
, which maps the model of the object of interest, represented by a set 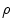 of
of 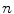 parameters describing its geometrical properties (e.g. position, rotation, scaling etc.), to image
parameters describing its geometrical properties (e.g. position, rotation, scaling etc.), to image 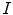 in
in 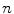 -dimensional parameter space. The most straightforward but computationally demanding approach for optimizing
-dimensional parameter space. The most straightforward but computationally demanding approach for optimizing 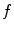 is to apply brute force to compute its response for all
is to apply brute force to compute its response for all 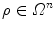 , where
, where 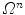 is a bounded domain in the parameter space. Alternative approaches [1, 2] often compute function responses in a neighborhood of an initial set
is a bounded domain in the parameter space. Alternative approaches [1, 2] often compute function responses in a neighborhood of an initial set 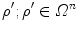 , predict the optimal
, predict the optimal 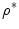 and iteratively move towards
and iteratively move towards 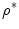 . Although such optimization is computationally not demanding and may, especially if
. Although such optimization is computationally not demanding and may, especially if 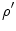 is relatively close to
is relatively close to 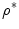 , lead to the globally optimal solution, it may still converge to local optima. Therefore, there is a need to observe the whole
, lead to the globally optimal solution, it may still converge to local optima. Therefore, there is a need to observe the whole 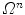 and, at the same time, minimize actual computations of
and, at the same time, minimize actual computations of 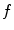 . To overcome these problems, we propose a novel optimization scheme that is based on interpolation theory [3]. The proposed optimization scheme does not depend on initialization and observes the whole
. To overcome these problems, we propose a novel optimization scheme that is based on interpolation theory [3]. The proposed optimization scheme does not depend on initialization and observes the whole 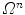 , and we apply it for spine and vertebra detection in 3D spine images. Depending on the objective function
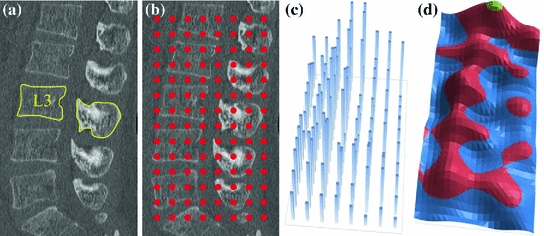
, and we apply it for spine and vertebra detection in 3D spine images. Depending on the objective function 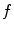 , the scheme searches for optima in the form of either minima or maxima, however, we will refer to them as maxima in the following text.
, the scheme searches for optima in the form of either minima or maxima, however, we will refer to them as maxima in the following text.
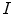 can be, in general, performed by optimizing an objective function
can be, in general, performed by optimizing an objective function 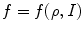 , which maps the model of the object of interest, represented by a set
, which maps the model of the object of interest, represented by a set 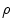 of
of 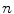 parameters describing its geometrical properties (e.g. position, rotation, scaling etc.), to image
parameters describing its geometrical properties (e.g. position, rotation, scaling etc.), to image 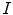 in
in 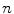 -dimensional parameter space. The most straightforward but computationally demanding approach for optimizing
-dimensional parameter space. The most straightforward but computationally demanding approach for optimizing 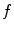 is to apply brute force to compute its response for all
is to apply brute force to compute its response for all 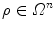 , where
, where 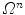 is a bounded domain in the parameter space. Alternative approaches [1, 2] often compute function responses in a neighborhood of an initial set
is a bounded domain in the parameter space. Alternative approaches [1, 2] often compute function responses in a neighborhood of an initial set 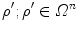 , predict the optimal
, predict the optimal 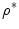 and iteratively move towards
and iteratively move towards 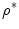 . Although such optimization is computationally not demanding and may, especially if
. Although such optimization is computationally not demanding and may, especially if 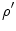 is relatively close to
is relatively close to 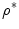 , lead to the globally optimal solution, it may still converge to local optima. Therefore, there is a need to observe the whole
, lead to the globally optimal solution, it may still converge to local optima. Therefore, there is a need to observe the whole 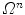 and, at the same time, minimize actual computations of
and, at the same time, minimize actual computations of 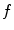 . To overcome these problems, we propose a novel optimization scheme that is based on interpolation theory [3]. The proposed optimization scheme does not depend on initialization and observes the whole
. To overcome these problems, we propose a novel optimization scheme that is based on interpolation theory [3]. The proposed optimization scheme does not depend on initialization and observes the whole 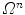 , and we apply it for spine and vertebra detection in 3D spine images. Depending on the objective function
, and we apply it for spine and vertebra detection in 3D spine images. Depending on the objective function 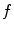 , the scheme searches for optima in the form of either minima or maxima, however, we will refer to them as maxima in the following text.
, the scheme searches for optima in the form of either minima or maxima, however, we will refer to them as maxima in the following text.
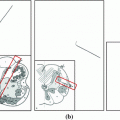
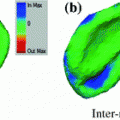
Fig. 1
An illustration of the L3 vertebra detection. a Reference segmentation binary mask, overlayed onto a selected sagittal cross-section of the CT image. b The interpolation grid. c The objective function 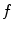 is computed only for nodes forming the interpolation grid. d The local maxima of the interpolation function
is computed only for nodes forming the interpolation grid. d The local maxima of the interpolation function 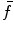 indicate candidate locations of the observed vertebra. In this case, the global maximum (in green) does not correspond to the location of L3 (Color figure online)
indicate candidate locations of the observed vertebra. In this case, the global maximum (in green) does not correspond to the location of L3 (Color figure online)
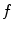 is computed only for nodes forming the interpolation grid. d The local maxima of the interpolation function
is computed only for nodes forming the interpolation grid. d The local maxima of the interpolation function 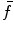 indicate candidate locations of the observed vertebra. In this case, the global maximum (in green) does not correspond to the location of L3 (Color figure online)
indicate candidate locations of the observed vertebra. In this case, the global maximum (in green) does not correspond to the location of L3 (Color figure online)2.1 Interpolation Theory
By assuming that the objective function 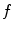 is smooth and its values are similar for similar sets
is smooth and its values are similar for similar sets 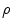 of parameters,
of parameters, 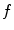 can be approximated by function
can be approximated by function 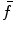 if the response of
if the response of 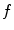 is known for a limited set of nodes
is known for a limited set of nodes 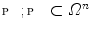 (Fig. 1). If nodes in
(Fig. 1). If nodes in 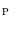 are selected properly, the difference between
are selected properly, the difference between 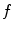 and its approximation
and its approximation 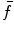 , i.e. the interpolation error, is relatively small, and the maximum of
, i.e. the interpolation error, is relatively small, and the maximum of 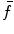 corresponds to the maximum of
corresponds to the maximum of 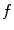 at the same point
at the same point 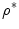 . The main concept of interpolation theory [3] is to select the interpolation function, in our case
. The main concept of interpolation theory [3] is to select the interpolation function, in our case 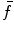 , from a given class of functions so that its response passes through the nodes in
, from a given class of functions so that its response passes through the nodes in 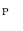 , which form the interpolation grid over the observed domain
, which form the interpolation grid over the observed domain 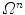 . However, interpolation of high-dimensional functions is computationally challenging, as the number of nodes grows exponentially with the increasing number of dimensions
. However, interpolation of high-dimensional functions is computationally challenging, as the number of nodes grows exponentially with the increasing number of dimensions 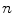 . To reduce the computational complexity, various strategies can be applied [4, 5], but in our case we take into account the properties of spine detection. The standard spine image acquisition procedure restricts the orientation of the imaged subject, and therefore the relative inclination of the spinal column in the image is more constant than its position, and similarly the orientation of a vertebra is restricted by the position of neighboring vertebrae. It can be concluded that dimensions related to object translation have to be associated with a larger number of interpolation nodes than dimensions related to object rotations. To optimize the objective function
. To reduce the computational complexity, various strategies can be applied [4, 5], but in our case we take into account the properties of spine detection. The standard spine image acquisition procedure restricts the orientation of the imaged subject, and therefore the relative inclination of the spinal column in the image is more constant than its position, and similarly the orientation of a vertebra is restricted by the position of neighboring vertebrae. It can be concluded that dimensions related to object translation have to be associated with a larger number of interpolation nodes than dimensions related to object rotations. To optimize the objective function 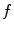 , defined on domain
, defined on domain 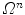 of
of 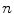 dimensions, we therefore propose the following algorithm:
dimensions, we therefore propose the following algorithm:
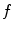 is smooth and its values are similar for similar sets
is smooth and its values are similar for similar sets 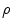 of parameters,
of parameters, 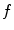 can be approximated by function
can be approximated by function 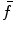 if the response of
if the response of 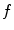 is known for a limited set of nodes
is known for a limited set of nodes 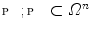 (Fig. 1). If nodes in
(Fig. 1). If nodes in 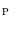 are selected properly, the difference between
are selected properly, the difference between 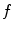 and its approximation
and its approximation 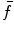 , i.e. the interpolation error, is relatively small, and the maximum of
, i.e. the interpolation error, is relatively small, and the maximum of 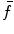 corresponds to the maximum of
corresponds to the maximum of 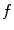 at the same point
at the same point 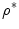 . The main concept of interpolation theory [3] is to select the interpolation function, in our case
. The main concept of interpolation theory [3] is to select the interpolation function, in our case 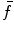 , from a given class of functions so that its response passes through the nodes in
, from a given class of functions so that its response passes through the nodes in 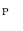 , which form the interpolation grid over the observed domain
, which form the interpolation grid over the observed domain 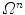 . However, interpolation of high-dimensional functions is computationally challenging, as the number of nodes grows exponentially with the increasing number of dimensions
. However, interpolation of high-dimensional functions is computationally challenging, as the number of nodes grows exponentially with the increasing number of dimensions 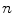 . To reduce the computational complexity, various strategies can be applied [4, 5], but in our case we take into account the properties of spine detection. The standard spine image acquisition procedure restricts the orientation of the imaged subject, and therefore the relative inclination of the spinal column in the image is more constant than its position, and similarly the orientation of a vertebra is restricted by the position of neighboring vertebrae. It can be concluded that dimensions related to object translation have to be associated with a larger number of interpolation nodes than dimensions related to object rotations. To optimize the objective function
. To reduce the computational complexity, various strategies can be applied [4, 5], but in our case we take into account the properties of spine detection. The standard spine image acquisition procedure restricts the orientation of the imaged subject, and therefore the relative inclination of the spinal column in the image is more constant than its position, and similarly the orientation of a vertebra is restricted by the position of neighboring vertebrae. It can be concluded that dimensions related to object translation have to be associated with a larger number of interpolation nodes than dimensions related to object rotations. To optimize the objective function 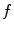 , defined on domain
, defined on domain 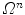 of
of 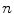 dimensions, we therefore propose the following algorithm:
dimensions, we therefore propose the following algorithm:1.
Initialize set 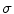 of optimized dimensions as
of optimized dimensions as 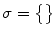 , and set
, and set 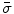 of the remaining dimensions as
of the remaining dimensions as 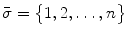 .
.
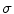 of optimized dimensions as
of optimized dimensions as 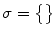 , and set
, and set 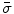 of the remaining dimensions as
of the remaining dimensions as 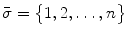 .
.2.
Interpolate 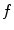 with
with 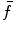 against the first
against the first 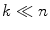 dimensions.
dimensions.
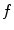 with
with 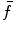 against the first
against the first 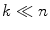 dimensions.
dimensions.3.
Find 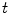 local maxima of
local maxima of 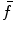 , then insert the observed dimensions into
, then insert the observed dimensions into 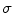 ;
; 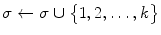 , and remove them from
, and remove them from 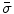 ;
; 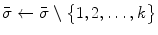 .
.
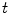 local maxima of
local maxima of 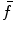 , then insert the observed dimensions into
, then insert the observed dimensions into 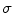 ;
; 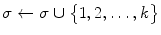 , and remove them from
, and remove them from 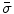 ;
; 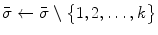 .
.4.
For each local maximum among 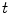 , perform the following steps:
, perform the following steps:
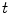 , perform the following steps:
, perform the following steps:4a.
If 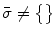 , take the next
, take the next 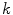 available dimensions and interpolate
available dimensions and interpolate 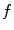 with
with 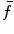 by considering dimensions from
by considering dimensions from 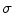 to be optimized.
to be optimized.
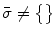 , take the next
, take the next 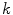 available dimensions and interpolate
available dimensions and interpolate 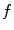 with
with 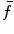 by considering dimensions from
by considering dimensions from 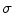 to be optimized.
to be optimized.4b.
Find the global maximum of 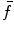 , insert the observed dimensions into
, insert the observed dimensions into 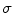 and remove them from
and remove them from 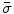 . Return to step 4a.
. Return to step 4a.
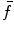 , insert the observed dimensions into
, insert the observed dimensions into 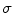 and remove them from
and remove them from 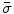 . Return to step 4a.
. Return to step 4a.5.
The resulting global maxima represent the locations of 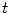 local maxima of
local maxima of 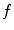 .
.
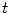 local maxima of
local maxima of 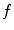 .
.In the proposed algorithm, the optimization dimensions have to be ordered according to the decreasing number of corresponding interpolation nodes, while the number of dimensions 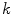 considered in each interpolation step may vary for different steps. Nevertheless, by taking into account only
considered in each interpolation step may vary for different steps. Nevertheless, by taking into account only 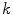 dimensions at once, the computational complexity of the high-dimensional optimization problem is reduced.
dimensions at once, the computational complexity of the high-dimensional optimization problem is reduced.
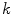 considered in each interpolation step may vary for different steps. Nevertheless, by taking into account only
considered in each interpolation step may vary for different steps. Nevertheless, by taking into account only 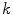 dimensions at once, the computational complexity of the high-dimensional optimization problem is reduced.
dimensions at once, the computational complexity of the high-dimensional optimization problem is reduced.2.2 Mean Shape Model of the Lumbar Spine
Let set 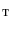 contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in
contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in 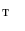 , the marching cubes algorithm [6] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [7], and the coherent point drift algorithm [8] is used to recover the nonrigid transformation among sets of vertices and establish point wise correspondences among vertices of the same vertebral level. Finally, the generalized Procrustes alignment [9] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh
, the marching cubes algorithm [6] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [7], and the coherent point drift algorithm [8] is used to recover the nonrigid transformation among sets of vertices and establish point wise correspondences among vertices of the same vertebral level. Finally, the generalized Procrustes alignment [9] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh 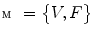 of
of 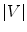 vertices and
vertices and 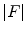 faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while mean shape models of individual vertebrae are used for vertebra detection in an unknown 3D image
faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while mean shape models of individual vertebrae are used for vertebra detection in an unknown 3D image 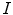 .
.
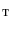 contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in
contain 3D images of the lumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual lumbar vertebra from level L1 to L5. To extract a shape model of each vertebra from each image in 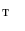 , the marching cubes algorithm [6] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [7], and the coherent point drift algorithm [8] is used to recover the nonrigid transformation among sets of vertices and establish point wise correspondences among vertices of the same vertebral level. Finally, the generalized Procrustes alignment [9] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh
, the marching cubes algorithm [6] is applied to each corresponding binary mask, resulting in a 3D face-vertex mesh consisting of vertices with triangle connectivity information. The dependency of the number of vertices in each mesh on the size of the image voxel and of the observed vertebra is removed by isotropic remeshing [7], and the coherent point drift algorithm [8] is used to recover the nonrigid transformation among sets of vertices and establish point wise correspondences among vertices of the same vertebral level. Finally, the generalized Procrustes alignment [9] is used to remove translation, rotation and scaling from corresponding meshes, yielding the mean shape model of each vertebra, represented by a 3D face-vertex mesh 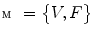 of
of 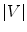 vertices and
vertices and 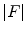 faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while mean shape models of individual vertebrae are used for vertebra detection in an unknown 3D image
faces (i.e. triangles). The mean shape model of the whole lumbar spine, i.e. a chain of mean shape models of individual vertebrae, is further used for spine detection, while mean shape models of individual vertebrae are used for vertebra detection in an unknown 3D image 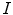 .
.2.3 Spine Detection
Let the 3D mesh 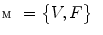 represent the mean shape model of the lumbar spine (Sect. 2.2), i.e. a chain of meshes representing individual vertebrae from L1 to L5. The objective function
represent the mean shape model of the lumbar spine (Sect. 2.2), i.e. a chain of meshes representing individual vertebrae from L1 to L5. The objective function 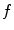 that measures the agreement between mesh
that measures the agreement between mesh 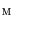 and image
and image 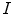 is defined as:
is defined as:
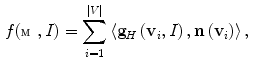
where 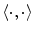 denotes the dot product,
denotes the dot product, 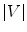 is the number of mesh vertices,
is the number of mesh vertices, 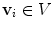 is a mesh vertex,
is a mesh vertex, 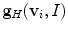 is the Haar-like gradient [10] of image
is the Haar-like gradient [10] of image 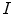 at the location of vertex
at the location of vertex 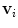 , and
, and 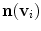 is the mesh normal at vertex
is the mesh normal at vertex 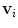 . If mesh
. If mesh 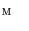 is correctly aligned with the spine in image
is correctly aligned with the spine in image 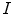 , then mesh normals pointing outwards of the mesh are in maximal agreement with the Haar-like gradients pointing outwards of the spine, resulting in the maximum of the objective function
, then mesh normals pointing outwards of the mesh are in maximal agreement with the Haar-like gradients pointing outwards of the spine, resulting in the maximum of the objective function 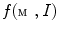 . As Haar-like gradients are described as a difference between two neighboring cuboids instead of two neighboring voxels, they are not sensitive to local intensity fluctuations and therefore make spine detection more robust.
. As Haar-like gradients are described as a difference between two neighboring cuboids instead of two neighboring voxels, they are not sensitive to local intensity fluctuations and therefore make spine detection more robust.
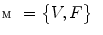 represent the mean shape model of the lumbar spine (Sect. 2.2), i.e. a chain of meshes representing individual vertebrae from L1 to L5. The objective function
represent the mean shape model of the lumbar spine (Sect. 2.2), i.e. a chain of meshes representing individual vertebrae from L1 to L5. The objective function 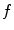 that measures the agreement between mesh
that measures the agreement between mesh 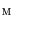 and image
and image 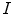 is defined as:
is defined as: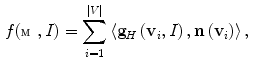
(1)
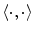 denotes the dot product,
denotes the dot product, 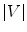 is the number of mesh vertices,
is the number of mesh vertices, 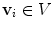 is a mesh vertex,
is a mesh vertex, 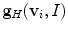 is the Haar-like gradient [10] of image
is the Haar-like gradient [10] of image 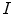 at the location of vertex
at the location of vertex 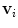 , and
, and 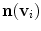 is the mesh normal at vertex
is the mesh normal at vertex 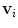 . If mesh
. If mesh 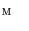 is correctly aligned with the spine in image
is correctly aligned with the spine in image 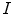 , then mesh normals pointing outwards of the mesh are in maximal agreement with the Haar-like gradients pointing outwards of the spine, resulting in the maximum of the objective function
, then mesh normals pointing outwards of the mesh are in maximal agreement with the Haar-like gradients pointing outwards of the spine, resulting in the maximum of the objective function 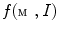 . As Haar-like gradients are described as a difference between two neighboring cuboids instead of two neighboring voxels, they are not sensitive to local intensity fluctuations and therefore make spine detection more robust.
. As Haar-like gradients are described as a difference between two neighboring cuboids instead of two neighboring voxels, they are not sensitive to local intensity fluctuations and therefore make spine detection more robust.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree