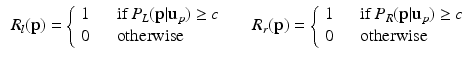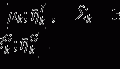Fig. 1.
Laparoscopic images of the uterus. FU-junctions are shown in blue and green for left and right respectively. The detection difficulty comes from ligament junctions, variation in the Fallopian tube orientations and their width. Images (a-d) illustrate inter-patient appearance variation.
2 Background and Related Work
Registering Preoperative Images in Laparoscopic Surgery. Existing methods for tackling this problem follow a common pipeline. First the organ is semi-automatically segmented in the preoperative image and a mesh model of its surface is constructed. A deformable model is also constructed to model the non-rigid 3D transform that maps points in the organ to their positions in the laparoscope’s coordinate frame. Most methods require stereo laparoscopic images [11, 12, 18] because these can provide intraoperative 3D surface information. Recently methods have been proposed for monocular laparoscopes [5]. The registration problem is considerably more challenging with monocular laparoscopes. However the application is broader because the overwhelming majority of laparoscopic surgery is performed with monocular laparoscopes. All methods require a suitable deformation model to constrain the organ’s shape. These have included biomechanical models [11, 12], 3D splines or affine transforms [5]. Organs which have been studied include the liver [12], kidney [11] and uterus [5]. A limitation with all the above methods is that they assume the organ is visible in the laparoscopic images and that there is a manual operator on hand to locate anatomical landmarks.
Detecting Objects in Optical Images. Detecting objects in optical images is a long-standing problem in computer vision that spans several decades of research. In recent years Deformable Part Models (DPMs) have emerged as the best-performing general-purpose object detector [3, 9]. DPMs work by modeling the shape variation of an object class with a set of simple parts that are linked with geometric constraints. Each part models the appearance of the object within a local region. The parts can move to handle geometric variation caused by shape and viewpoint changes. DPMs currently are the best performing detectors in the Pascal Challenge dataset [8], and have been used successfully in other areas of medical imaging such as lung nodule classification [20] and fetal nuchal translucency [7]. However their application to organ detection in laparoscopic images has not yet been investigated.
Junction Detection in Optical Images. There are three main classes of methods for junction detection in optical images. The first are corner-based methods which measure ‘cornerness’ using the image structure tensor [13]. Junctions are then detected as image points with high degree of cornerness. The second are contour-based methods which detect junctions as intersection of image contours [2]. The third are template-based methods which model junctions with a set of templates that correspond to specific junction geometries such as ‘Y’ or ‘T’-shaped, and are learned from natural images [19]. We found that the above classes of methods are not suitable for detecting FU-junctions (Fig. 2). This is for two reasons: (i) they are not discriminative enough to separate FU-junctions from other junctions, such as vascular bifurcations, so they give many false positives and (ii) they cannot handle well the appearance variation of FU-junctions (Fig. 1).
3 Detection Framework
We propose a learning-based fully-automatic system to detect the uterus and FU-junctions. This is based on four concepts: (i) the uterus can be detected prior to FU-junction detection. (ii) FU-junctions are too difficult to be detected with generic corner detectors such as [2, 13, 19], so they should be detected with a learned model. (iii) FU-junctions are always located close to tube-like structures, so we can filter out many incorrect FU-junction locations if they exist far from tube-like structures. (iv) There exist contextual constraints between the uterus body and FU-junctions. We use two types of contextual constraints. The first models the conditional probability of an FU-junction occurring at a position in the image given the uterus center. Given a uterus detection we can eliminate pixel locations which have low conditional probability giving us Regions of Interest (ROIs) for the locations of FU-junctions. The second contextual constraint encodes the fact that FU-junctions are on the uterus surface, which means there should usually exist a path in the image that connects them to the uterus center which does not cross an object boundary.
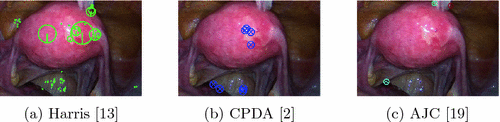

Fig. 2.
Failure of generic junction detectors to detect FU-junctions.
Automatically detecting the uterus and FU-junctions is not an easy problem to solve due to large inter-patient anatomic variability (both in shape and texture) (Fig. 1). We restrict the scope of the problem to images of the uterus before resection. This means that the uterus has not changed topologically by surgical incisions. We also assume the uterus is not significantly occluded by surgical tools. In uterine surgery the laparoscope is nearly always held in upright position, so our detectors do not need to be invariant to high degrees of rotations about the laparoscope’s optical axis.
We outline the full proposed detection process in Fig. 3. This consists of two main steps: (i) uterus detection and (ii) FU-junction detection. We use a trained DPM model to detect the whole uterus, its center and its bounding box. We then proceed to detect the FU-junctions using contextual constraints and a number of processing steps which reduce the search space for FU-junction locations. We then compute local and contextual features for all candidate locations and perform classification with a sparse linear SVM.
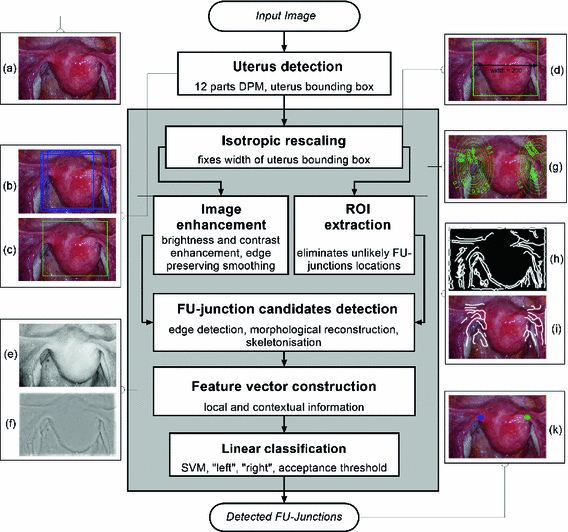

Fig. 3.
Diagram of the main pipeline of the proposed detection process.
3.1 The Uterus Detector
Given an input laparoscopic image (Fig. 3 (a)) we use a trained DPM model to detect the uterus body. This is achieved with an open-source implementation of [10] and a set of annotated uterus images (details of the dataset are given in Sect. 4.1). The detector scans the image at multiple scales and positions and returns bounding boxes (Fig. 3 (b)) around positive detections and their corresponding detection scores. We select the bounding box with the highest detection score 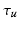 , and if
, and if 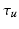 is greater than an acceptance threshold
is greater than an acceptance threshold 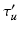 the detection is kept (Fig. 3 (c)), otherwise it is rejected (details for computing
the detection is kept (Fig. 3 (c)), otherwise it is rejected (details for computing 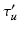 are in Sect. 4.1). We use
are in Sect. 4.1). We use 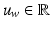 ,
, 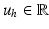 and
and 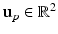 to denote the uterus bounding box width, height and center outputted from the DPM uterus detector. We then proceed to detect the FU-junctions.
to denote the uterus bounding box width, height and center outputted from the DPM uterus detector. We then proceed to detect the FU-junctions.
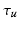 , and if
, and if 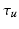 is greater than an acceptance threshold
is greater than an acceptance threshold 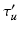 the detection is kept (Fig. 3 (c)), otherwise it is rejected (details for computing
the detection is kept (Fig. 3 (c)), otherwise it is rejected (details for computing 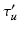 are in Sect. 4.1). We use
are in Sect. 4.1). We use 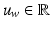 ,
, 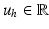 and
and 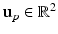 to denote the uterus bounding box width, height and center outputted from the DPM uterus detector. We then proceed to detect the FU-junctions.
to denote the uterus bounding box width, height and center outputted from the DPM uterus detector. We then proceed to detect the FU-junctions.3.2 The FU-junction Detector
Step 1: Isotropic Rescaling. First the image is isotropically rescaled so the bounding box of the uterus has a default width of 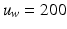 pixels (Fig. 3 (d)). This fixes the scale of the uterus and allows us to detect FU-junctions without requiring detection at multiple scales. This has the benefit of increasing computation speed and reducing false positives.
pixels (Fig. 3 (d)). This fixes the scale of the uterus and allows us to detect FU-junctions without requiring detection at multiple scales. This has the benefit of increasing computation speed and reducing false positives.
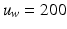 pixels (Fig. 3 (d)). This fixes the scale of the uterus and allows us to detect FU-junctions without requiring detection at multiple scales. This has the benefit of increasing computation speed and reducing false positives.
pixels (Fig. 3 (d)). This fixes the scale of the uterus and allows us to detect FU-junctions without requiring detection at multiple scales. This has the benefit of increasing computation speed and reducing false positives.Step 2: Image Enhancement. We enhance the image with contrast stretching on the red channel (Fig. 3 (e)). We perform coarse illumination correction to remove uneven illumination with low pass filtering. We then perform edge preserving smoothing using the guided filter method from Matlab (Fig. 3 (f)). We use only the red channel because it is mostly insensitive to the uterus’ natural texture variation (unlike the green and blue channels [4]). This means that strong edges in the red channel are highly indicative of object boundaries.
Step 3: ROI Extraction. We filter out highly improbable locations for the left and right FU-junctions. For each pixel 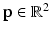 in the image we compute the conditional probability
in the image we compute the conditional probability 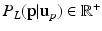 of the left junction occurring at
of the left junction occurring at 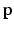 given
given 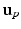 . This is a contextual constraint that we model with a Gaussian Mixture Model (GMM):
. This is a contextual constraint that we model with a Gaussian Mixture Model (GMM):
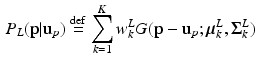
where K is the number of GMM components and 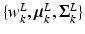 are the GMM parameters. We keep
are the GMM parameters. We keep 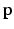 as a left junction candidate if
as a left junction candidate if 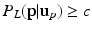 , where c is a small probability threshold. For the right FU-junction we also use a GMM to model the conditional probability
, where c is a small probability threshold. For the right FU-junction we also use a GMM to model the conditional probability 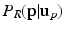 of the FU-junction occurring at
of the FU-junction occurring at 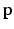 . To train the GMM parameters we exploit the fact that the FU-junctions have strong bilateral symmetry about the uterus body (Fig. 1). Because the laparoscope is normally in upright position this implies the FU-junctions are horizontally symmetric. We therefore propose to simplify the model with
. To train the GMM parameters we exploit the fact that the FU-junctions have strong bilateral symmetry about the uterus body (Fig. 1). Because the laparoscope is normally in upright position this implies the FU-junctions are horizontally symmetric. We therefore propose to simplify the model with 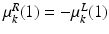 ,
, 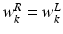 and
and 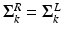 . The advantage of doing this is that we effectively double the amount of training data. This is because each training example can now be used to train
. The advantage of doing this is that we effectively double the amount of training data. This is because each training example can now be used to train 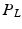 and
and 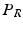 by reflecting its position horizontally relative to
by reflecting its position horizontally relative to 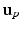 . Training is performed with the standard K-means/EM algorithm on the training set. We set c using a training dataset (see Sect. 4.1) at the 99 % percentile cut-off point. We select K automatically such that it minimizes the cross-validation error using a hold-out training set (see Sect. 4.1). We then compute two ROIs (Fig. 3 (g)),
. Training is performed with the standard K-means/EM algorithm on the training set. We set c using a training dataset (see Sect. 4.1) at the 99 % percentile cut-off point. We select K automatically such that it minimizes the cross-validation error using a hold-out training set (see Sect. 4.1). We then compute two ROIs (Fig. 3 (g)), 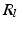 and
and 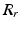 for the left and right FU-junctions respectively, with
for the left and right FU-junctions respectively, with
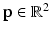 in the image we compute the conditional probability
in the image we compute the conditional probability 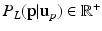 of the left junction occurring at
of the left junction occurring at 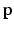 given
given 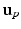 . This is a contextual constraint that we model with a Gaussian Mixture Model (GMM):
. This is a contextual constraint that we model with a Gaussian Mixture Model (GMM):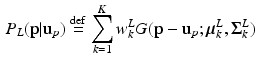
(1)
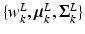 are the GMM parameters. We keep
are the GMM parameters. We keep 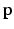 as a left junction candidate if
as a left junction candidate if 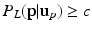 , where c is a small probability threshold. For the right FU-junction we also use a GMM to model the conditional probability
, where c is a small probability threshold. For the right FU-junction we also use a GMM to model the conditional probability 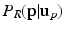 of the FU-junction occurring at
of the FU-junction occurring at 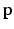 . To train the GMM parameters we exploit the fact that the FU-junctions have strong bilateral symmetry about the uterus body (Fig. 1). Because the laparoscope is normally in upright position this implies the FU-junctions are horizontally symmetric. We therefore propose to simplify the model with
. To train the GMM parameters we exploit the fact that the FU-junctions have strong bilateral symmetry about the uterus body (Fig. 1). Because the laparoscope is normally in upright position this implies the FU-junctions are horizontally symmetric. We therefore propose to simplify the model with 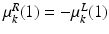 ,
, 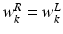 and
and 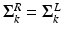 . The advantage of doing this is that we effectively double the amount of training data. This is because each training example can now be used to train
. The advantage of doing this is that we effectively double the amount of training data. This is because each training example can now be used to train 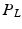 and
and 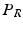 by reflecting its position horizontally relative to
by reflecting its position horizontally relative to 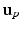 . Training is performed with the standard K-means/EM algorithm on the training set. We set c using a training dataset (see Sect. 4.1) at the 99 % percentile cut-off point. We select K automatically such that it minimizes the cross-validation error using a hold-out training set (see Sect. 4.1). We then compute two ROIs (Fig. 3 (g)),
. Training is performed with the standard K-means/EM algorithm on the training set. We set c using a training dataset (see Sect. 4.1) at the 99 % percentile cut-off point. We select K automatically such that it minimizes the cross-validation error using a hold-out training set (see Sect. 4.1). We then compute two ROIs (Fig. 3 (g)), 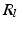 and
and 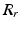 for the left and right FU-junctions respectively, with
for the left and right FU-junctions respectively, with