and 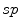 (cloud parameter and shadow parameter, in the order given), increasing the algorithm flexibility. The equation that describes this operation is:
(cloud parameter and shadow parameter, in the order given), increasing the algorithm flexibility. The equation that describes this operation is:
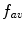 is the average value of image pixels,
is the average value of image pixels, 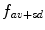 is the sum of the average value pixels and the standard deviation value of the image and
is the sum of the average value pixels and the standard deviation value of the image and 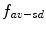 is the subtraction of the average value by the standard deviation pixels.
is the subtraction of the average value by the standard deviation pixels.The region labeled as 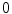 represents a shadow region, labeled as
represents a shadow region, labeled as 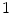 means region not affected by atmospheric interference, while regions labeled as
means region not affected by atmospheric interference, while regions labeled as 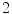 represents thin clouds, and dense cloud are labeled as
represents thin clouds, and dense cloud are labeled as 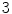 . For images with multiple bands these labels are assigned if and only if the rule is valid for all bands.
. For images with multiple bands these labels are assigned if and only if the rule is valid for all bands.
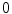 represents a shadow region, labeled as
represents a shadow region, labeled as 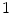 means region not affected by atmospheric interference, while regions labeled as
means region not affected by atmospheric interference, while regions labeled as 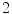 represents thin clouds, and dense cloud are labeled as
represents thin clouds, and dense cloud are labeled as 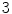 . For images with multiple bands these labels are assigned if and only if the rule is valid for all bands.
. For images with multiple bands these labels are assigned if and only if the rule is valid for all bands.To complete this process, it is applied a morphological opening operation that aims to remove very small objects that can cause mistakes in following steps.
2.2 Image Decomposition
The method proposed by Vese and Osher [18] decomposes an image into two sub-images, each representing the components of structure or texture, thus, a better image redefinition can be made. On the structured part, should be applied the technique of inpainting based on DCT, whilst into texture portions and heterogeneous areas is suitable to use texture synthesis.
The generalized model is defined as:
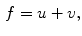
where 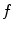 is the input image,
is the input image, 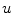 is the structure image and
is the structure image and 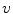 is the texture image. So, given these sub-images one can reconstruct the original image. However, in practice it is observed that the original image can be only approximately reconstructed. The goal of the method is to have a structure image
is the texture image. So, given these sub-images one can reconstruct the original image. However, in practice it is observed that the original image can be only approximately reconstructed. The goal of the method is to have a structure image 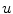 that preserves all strong edges with smoothed internal regions, and an image
that preserves all strong edges with smoothed internal regions, and an image 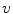 that contains all the texture and noise information.
that contains all the texture and noise information.
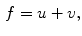
(2)
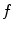 is the input image,
is the input image, 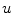 is the structure image and
is the structure image and 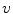 is the texture image. So, given these sub-images one can reconstruct the original image. However, in practice it is observed that the original image can be only approximately reconstructed. The goal of the method is to have a structure image
is the texture image. So, given these sub-images one can reconstruct the original image. However, in practice it is observed that the original image can be only approximately reconstructed. The goal of the method is to have a structure image 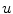 that preserves all strong edges with smoothed internal regions, and an image
that preserves all strong edges with smoothed internal regions, and an image 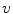 that contains all the texture and noise information.
that contains all the texture and noise information.The method used to construct the structured image 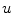 is based on the assumption that
is based on the assumption that 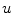 is a
is a 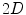 function and in attempt to minimize this function in the space of all Bounded Variation functions (BV). Functions in BV space are functions whose total variation are limited by some constant value less than infinity. Minimizing
function and in attempt to minimize this function in the space of all Bounded Variation functions (BV). Functions in BV space are functions whose total variation are limited by some constant value less than infinity. Minimizing 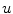 in BV space ensures resulting in a stable image and without infinite values. It should be noted, however, that this space allows for functions which have very large derivatives (although non-infinite), thereby ensuring that strong edges are preserved.
in BV space ensures resulting in a stable image and without infinite values. It should be noted, however, that this space allows for functions which have very large derivatives (although non-infinite), thereby ensuring that strong edges are preserved.
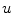 is based on the assumption that
is based on the assumption that 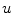 is a
is a 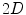 function and in attempt to minimize this function in the space of all Bounded Variation functions (BV). Functions in BV space are functions whose total variation are limited by some constant value less than infinity. Minimizing
function and in attempt to minimize this function in the space of all Bounded Variation functions (BV). Functions in BV space are functions whose total variation are limited by some constant value less than infinity. Minimizing 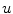 in BV space ensures resulting in a stable image and without infinite values. It should be noted, however, that this space allows for functions which have very large derivatives (although non-infinite), thereby ensuring that strong edges are preserved.
in BV space ensures resulting in a stable image and without infinite values. It should be noted, however, that this space allows for functions which have very large derivatives (although non-infinite), thereby ensuring that strong edges are preserved.Taking in mind the intuition described above, the minimization problem should logically have two terms. One of them will be the fidelity, responsible for maintaining the difference between 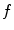 and
and 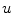 small. This term ensure that data of the input image are kept on result. The other one imply a smoothing over
small. This term ensure that data of the input image are kept on result. The other one imply a smoothing over 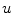 , although not necessarily in all
, although not necessarily in all 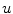 components. The minimization is computed as [14]:
components. The minimization is computed as [14]:
![$$\begin{aligned} F(u) = \left[ (\int {|\nabla u|}) + (\lambda \int {|f - u|^2})\right] dxdy, \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_15_Chapter_Equ3.gif)
with 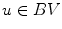 and
and 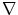 representing the gradient operator. The second term is the data term and the first one is a regularization term to ensure a relatively smooth image.
representing the gradient operator. The second term is the data term and the first one is a regularization term to ensure a relatively smooth image. 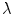 is a tuning parameter. As can be seen, this seeks find the optimal
is a tuning parameter. As can be seen, this seeks find the optimal 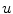 and ignores the
and ignores the 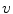 image. The reason is that, in Vese and Osher [18], the authors had considered the
image. The reason is that, in Vese and Osher [18], the authors had considered the 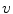 image to be noise, and therefore to be discarded.
image to be noise, and therefore to be discarded.
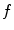 and
and 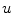 small. This term ensure that data of the input image are kept on result. The other one imply a smoothing over
small. This term ensure that data of the input image are kept on result. The other one imply a smoothing over 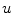 , although not necessarily in all
, although not necessarily in all 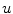 components. The minimization is computed as [14]:
components. The minimization is computed as [14]:![$$\begin{aligned} F(u) = \left[ (\int {|\nabla u|}) + (\lambda \int {|f - u|^2})\right] dxdy, \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_15_Chapter_Equ3.gif)
(3)
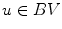 and
and 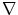 representing the gradient operator. The second term is the data term and the first one is a regularization term to ensure a relatively smooth image.
representing the gradient operator. The second term is the data term and the first one is a regularization term to ensure a relatively smooth image. 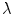 is a tuning parameter. As can be seen, this seeks find the optimal
is a tuning parameter. As can be seen, this seeks find the optimal 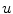 and ignores the
and ignores the 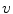 image. The reason is that, in Vese and Osher [18], the authors had considered the
image. The reason is that, in Vese and Osher [18], the authors had considered the 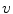 image to be noise, and therefore to be discarded.
image to be noise, and therefore to be discarded.There is an unique result to this optimization problem, and methods exist for finding the solution. Noting that 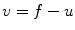 it is possible to easily modify the above equation to incorporate
it is possible to easily modify the above equation to incorporate 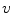 :
:
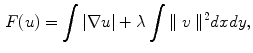
(still 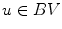 ). Which yields the Euler-Lagrange equation
). Which yields the Euler-Lagrange equation 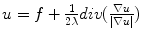 . Making the right manipulation
. Making the right manipulation 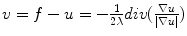 . At this point it is useful to break
. At this point it is useful to break 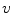 into its
into its 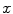 and
and 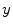 components respectively. It will be denoted as
components respectively. It will be denoted as 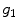 and
and 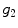 , where:
, where:
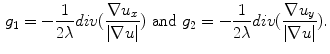
This allows us to write 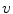 as:
as: 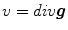 where
where 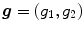 . It can be seen that
. It can be seen that 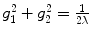 , so that
, so that 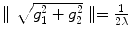 .
.
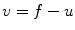 it is possible to easily modify the above equation to incorporate
it is possible to easily modify the above equation to incorporate 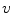 :
: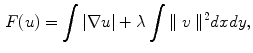
(4)
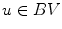 ). Which yields the Euler-Lagrange equation
). Which yields the Euler-Lagrange equation 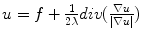 . Making the right manipulation
. Making the right manipulation 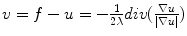 . At this point it is useful to break
. At this point it is useful to break 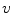 into its
into its 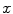 and
and 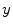 components respectively. It will be denoted as
components respectively. It will be denoted as 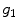 and
and 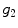 , where:
, where: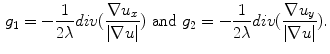
(5)
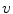 as:
as: 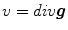 where
where 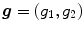 . It can be seen that
. It can be seen that 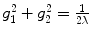 , so that
, so that 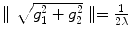 .
.This allows us to rewrite 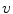 as:
as:
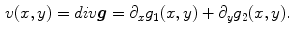
And leads to the final minimization problem (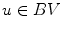 ):
):
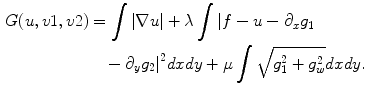
Solving the minimization problem (Eq. 7) yields the Euler-Lagrange equations:
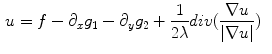
![$$\begin{aligned} \mu \frac{g_1}{\sqrt{g_1^2 + g_2^2}}&= 2\lambda [\frac{\partial }{\partial _x}(u-f) + \partial _{xx}^2 g_1 + \partial _{xy}^2 g_2] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_15_Chapter_Equ9.gif)
![$$\begin{aligned} \mu \frac{g_2}{\sqrt{g_1^2 + g_2^2}}&= 2\lambda [\frac{\partial }{\partial _y}(u-f) + \partial _{xy}^2 g_1 + \partial _{yy}^2 g_2] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_15_Chapter_Equ10.gif)
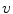 as:
as: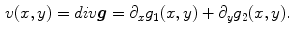
(6)
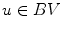 ):
):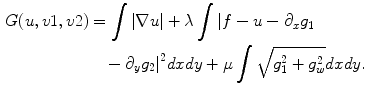
(7)
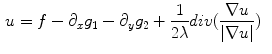
(8)
![$$\begin{aligned} \mu \frac{g_1}{\sqrt{g_1^2 + g_2^2}}&= 2\lambda [\frac{\partial }{\partial _x}(u-f) + \partial _{xx}^2 g_1 + \partial _{xy}^2 g_2] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_15_Chapter_Equ9.gif)
(9)
![$$\begin{aligned} \mu \frac{g_2}{\sqrt{g_1^2 + g_2^2}}&= 2\lambda [\frac{\partial }{\partial _y}(u-f) + \partial _{xy}^2 g_1 + \partial _{yy}^2 g_2] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_15_Chapter_Equ10.gif)
(10)
2.3 Inpainting by Smoothing Based on Multidimensional DCT
This method was proposed by Garcia [7], and so as in Bertalmio et al. [1], is based on the information propagation by smoothing. The specificity of this approach is related to the use of the Discrete Cosine Transform (DCT) to simplify and to solve linear systems, to an efficient smoothing.
2.3.1 Smoothing by Penalized Least Squares Regression
In statistics and data analysis, smoothing is used to reduce experimental noise or information and keeping the most important marks of the data set. Considering the following model for the one-dimensional noisy signal 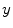 from the Eq. 11.
from the Eq. 11.
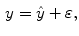
where 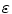 represents a Gaussian noise with zero mean and unknown variance, and
represents a Gaussian noise with zero mean and unknown variance, and 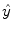 is the so-called smoothing, i.e., has continuous derivatives up to some order (usually
is the so-called smoothing, i.e., has continuous derivatives up to some order (usually 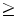 2) throughout the domain. The smoothing of
2) throughout the domain. The smoothing of 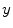 depends on the best estimate of
depends on the best estimate of 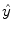 and this operation is usually performed by a parametric or nonparametric regression.
and this operation is usually performed by a parametric or nonparametric regression.
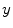 from the Eq. 11.
from the Eq. 11.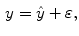
(11)
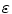 represents a Gaussian noise with zero mean and unknown variance, and
represents a Gaussian noise with zero mean and unknown variance, and 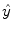 is the so-called smoothing, i.e., has continuous derivatives up to some order (usually
is the so-called smoothing, i.e., has continuous derivatives up to some order (usually 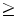 2) throughout the domain. The smoothing of
2) throughout the domain. The smoothing of 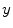 depends on the best estimate of
depends on the best estimate of 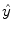 and this operation is usually performed by a parametric or nonparametric regression.
and this operation is usually performed by a parametric or nonparametric regression.A classic approach to smooth is the Penalized Least Squares Regression. This technique minimizes a criterion that balances the data fidelity, measured by the Residual Sum-of-Squares (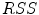 ) and by a penalty term (
) and by a penalty term (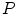 ), which reflects the robustness of the smoothed data. Another simple and straightforward approach to express the robustness is by using a Second-order Divided Difference (
), which reflects the robustness of the smoothed data. Another simple and straightforward approach to express the robustness is by using a Second-order Divided Difference (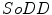 ), which produces an one-dimensional array of data.
), which produces an one-dimensional array of data.
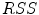 ) and by a penalty term (
) and by a penalty term (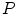 ), which reflects the robustness of the smoothed data. Another simple and straightforward approach to express the robustness is by using a Second-order Divided Difference (
), which reflects the robustness of the smoothed data. Another simple and straightforward approach to express the robustness is by using a Second-order Divided Difference (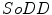 ), which produces an one-dimensional array of data.
), which produces an one-dimensional array of data.Now, using 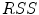 and the
and the 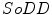 , the minimization of
, the minimization of 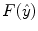 results in a linear system, expressed in Eq. 12, which allows the smoothed data determination.
results in a linear system, expressed in Eq. 12, which allows the smoothed data determination.
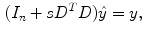
where 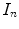 is the identity matrix
is the identity matrix 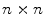 ,
, 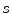 is a positive real scalar that controls the grade of smoothing, so that, as it increases, the degree of smoothing of
is a positive real scalar that controls the grade of smoothing, so that, as it increases, the degree of smoothing of 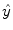 increases too; and
increases too; and 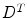 represents the transpose of
represents the transpose of 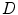 . Its important to note that
. Its important to note that 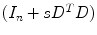 is a penta-diagonal symmetric matrix, and the last equation can be solved numerically in a computationally efficient way.
is a penta-diagonal symmetric matrix, and the last equation can be solved numerically in a computationally efficient way.
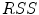 and the
and the 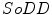 , the minimization of
, the minimization of 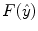 results in a linear system, expressed in Eq. 12, which allows the smoothed data determination.
results in a linear system, expressed in Eq. 12, which allows the smoothed data determination.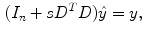
(12)
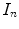 is the identity matrix
is the identity matrix 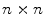 ,
, 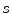 is a positive real scalar that controls the grade of smoothing, so that, as it increases, the degree of smoothing of
is a positive real scalar that controls the grade of smoothing, so that, as it increases, the degree of smoothing of 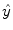 increases too; and
increases too; and 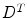 represents the transpose of
represents the transpose of 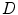 . Its important to note that
. Its important to note that 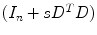 is a penta-diagonal symmetric matrix, and the last equation can be solved numerically in a computationally efficient way.
is a penta-diagonal symmetric matrix, and the last equation can be solved numerically in a computationally efficient way.2.3.2 Smoothing Equally Spaced Data
Equation 12 can be solved using the left division matrix applied to sparse matrices [7]. Solving this linear system, however, can be a lot of time expensive for a large amount of data. But, this algorithm can be simplified and accelerated, since the data are evenly spaced, in images where pixels are equally spaced, resulting in the following equation for multidimensional data:
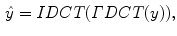
where DCT and IDCT




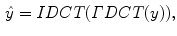
(13)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree