, such that 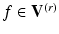 is a function at resolution r,
is a function at resolution r, ![$$r\in [0,R]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq3.gif) , with the level of detail increasing as r increases.
, with the level of detail increasing as r increases.
Let 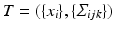 be a triangular surface mesh, where
be a triangular surface mesh, where 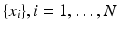 is a set of vertices and
is a set of vertices and 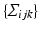 a set of simplices, with each simplex
a set of simplices, with each simplex 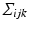 as a three tuple of points
as a three tuple of points 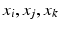 . Given a mesh
. Given a mesh 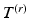 at level r, with coordinates
at level r, with coordinates ![$$X^{(r)} = [x_1,\dots , x_i, \dots ,x_{N^{(r)}}]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq10.gif) , where
, where 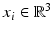 and
and 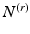 is the number of vertices on
is the number of vertices on 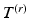 . The new vertices on
. The new vertices on 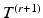 , denoted as
, denoted as 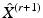 , can be given as
, can be given as
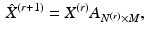
where A is an 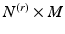 matrix for a simple subdivision scheme (where all elements of
matrix for a simple subdivision scheme (where all elements of 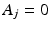 except for
except for 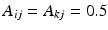 ) and M is the number of the new vertices on
) and M is the number of the new vertices on 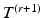 ,
, ![$$X^{(r+1)} = [X^{(r)},\hat{X}^{(r+1)}]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq20.gif) . Given an “averaging matrix”
. Given an “averaging matrix” 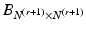 , a general subdivision scheme can be rewritten as
, a general subdivision scheme can be rewritten as
![$$\begin{aligned} X^{(r+1)} = X^{(r)}[I_{N^{(r)}\times N^{(r)}} \quad A]B = \tilde{X}^{(r+1)}B = X^{(r)}P^{(r)}, \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_Equ2.gif)
where ![$$\tilde{X}^{(r+1)} = X^{(r)}[I_{N^{(r)}\times N^{(r)}} \quad A]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq22.gif) ,
, ![$$P^{(r)} = [I_{N^{(r)}\times N^{(r)}} \quad A]B$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq23.gif) .
.
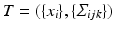 be a triangular surface mesh, where
be a triangular surface mesh, where 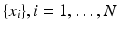 is a set of vertices and
is a set of vertices and 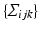 a set of simplices, with each simplex
a set of simplices, with each simplex 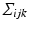 as a three tuple of points
as a three tuple of points 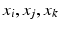 . Given a mesh
. Given a mesh 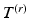 at level r, with coordinates
at level r, with coordinates ![$$X^{(r)} = [x_1,\dots , x_i, \dots ,x_{N^{(r)}}]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq10.gif) , where
, where 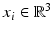 and
and 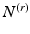 is the number of vertices on
is the number of vertices on 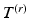 . The new vertices on
. The new vertices on 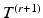 , denoted as
, denoted as 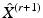 , can be given as
, can be given as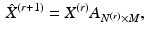
(1)
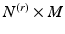 matrix for a simple subdivision scheme (where all elements of
matrix for a simple subdivision scheme (where all elements of 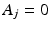 except for
except for 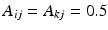 ) and M is the number of the new vertices on
) and M is the number of the new vertices on 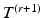 ,
, ![$$X^{(r+1)} = [X^{(r)},\hat{X}^{(r+1)}]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq20.gif) . Given an “averaging matrix”
. Given an “averaging matrix” 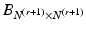 , a general subdivision scheme can be rewritten as
, a general subdivision scheme can be rewritten as![$$\begin{aligned} X^{(r+1)} = X^{(r)}[I_{N^{(r)}\times N^{(r)}} \quad A]B = \tilde{X}^{(r+1)}B = X^{(r)}P^{(r)}, \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_Equ2.gif)
(2)
![$$\tilde{X}^{(r+1)} = X^{(r)}[I_{N^{(r)}\times N^{(r)}} \quad A]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq22.gif) ,
, ![$$P^{(r)} = [I_{N^{(r)}\times N^{(r)}} \quad A]B$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq23.gif) .
.As explained in [12], surfaces can be parametrized with a function S(y), where y is defined on a base (coarsest) mesh 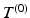 , i.e. y is a point on one of the simplices in
, i.e. y is a point on one of the simplices in 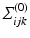 and can be tracked through a predefined subdivision process to a limit surface. We begin by first defining
and can be tracked through a predefined subdivision process to a limit surface. We begin by first defining 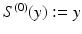 . Let
. Let 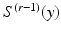 be found in a simplex
be found in a simplex 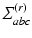 with vertices
with vertices 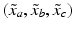 ,
, 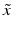 found in
found in 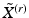 . Using the barycentric coordinates
. Using the barycentric coordinates 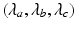 such that
such that 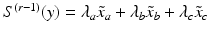 , we can induce a bijective map
, we can induce a bijective map 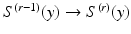 where
where
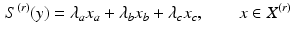
and 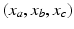 corresponds to
corresponds to 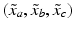 of the simplex
of the simplex 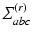 . Then,
. Then, 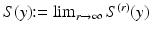 . In matrix form,
. In matrix form,
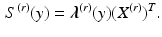
It follows that
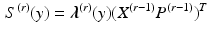
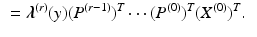
In other words, surfaces when parameterized into meshes, can be henceforth understood as functions from a small collection of triangles into 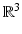 . The subdivision of triangles allows us to move from one resolution to another, providing a family of surfaces for registration. We show three resolutions of the brain cortex in Fig. 1.
. The subdivision of triangles allows us to move from one resolution to another, providing a family of surfaces for registration. We show three resolutions of the brain cortex in Fig. 1.
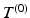 , i.e. y is a point on one of the simplices in
, i.e. y is a point on one of the simplices in 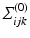 and can be tracked through a predefined subdivision process to a limit surface. We begin by first defining
and can be tracked through a predefined subdivision process to a limit surface. We begin by first defining 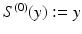 . Let
. Let 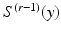 be found in a simplex
be found in a simplex 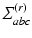 with vertices
with vertices 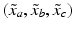 ,
, 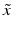 found in
found in 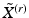 . Using the barycentric coordinates
. Using the barycentric coordinates 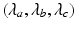 such that
such that 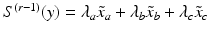 , we can induce a bijective map
, we can induce a bijective map 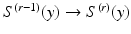 where
where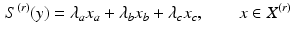
(3)
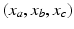 corresponds to
corresponds to 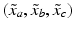 of the simplex
of the simplex 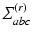 . Then,
. Then, 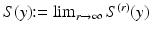 . In matrix form,
. In matrix form,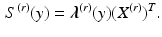
(4)
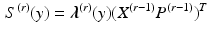
(5)
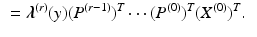
(6)
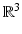 . The subdivision of triangles allows us to move from one resolution to another, providing a family of surfaces for registration. We show three resolutions of the brain cortex in Fig. 1.
. The subdivision of triangles allows us to move from one resolution to another, providing a family of surfaces for registration. We show three resolutions of the brain cortex in Fig. 1.
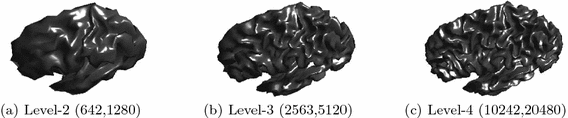
Fig. 1.
Increasing levels of 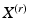 from left to right. Subcaptions indicates the corresponding levels, number of vertices, and number of faces – “Level-r (no. of vertices, no. of faces)”.
from left to right. Subcaptions indicates the corresponding levels, number of vertices, and number of faces – “Level-r (no. of vertices, no. of faces)”.
 from left to right. Subcaptions indicates the corresponding levels, number of vertices, and number of faces – “Level-r (no. of vertices, no. of faces)”.
from left to right. Subcaptions indicates the corresponding levels, number of vertices, and number of faces – “Level-r (no. of vertices, no. of faces)”.2.2 Multiresolution Large Deformation Diffeomorphic Metric Mapping for Surfaces
Now, we state a variational problem for mapping two surfaces under the framework of LDDMM. LDDMM assumes that transformation can be generated from one to another via flows of diffeomorphisms 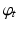 , which are solutions of ordinary differential equations
, which are solutions of ordinary differential equations ![$$\dot{\varphi }_t = v_t (\varphi _t), t \in [0,1],$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq42.gif) starting from the identity map
starting from the identity map 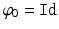 . They are therefore characterized by time-dependent velocity vector fields
. They are therefore characterized by time-dependent velocity vector fields ![$$v_t, t \in [0,1]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq44.gif) . We define a metric distance between a target surface
. We define a metric distance between a target surface 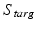 and an atlas surface
and an atlas surface 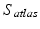 as the minimal length of curves
as the minimal length of curves ![$$\varphi _t \cdot S_{atlas}, t \in [0,1],$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq47.gif) in a shape space such that, at time
in a shape space such that, at time 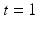 ,
, 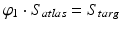 . Lengths of such curves are computed as the integrated norm
. Lengths of such curves are computed as the integrated norm 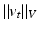 of the vector field, where
of the vector field, where 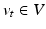 and V is a reproducing kernel Hilbert space with kernel
and V is a reproducing kernel Hilbert space with kernel 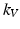 and norm
and norm 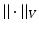 . To ensure solutions are diffeomorphisms, V must be a space of smooth vector fields. The duality isometry in Hilbert spaces allows us to express the lengths in terms of
. To ensure solutions are diffeomorphisms, V must be a space of smooth vector fields. The duality isometry in Hilbert spaces allows us to express the lengths in terms of 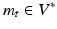 , interpreted as momentum such that
, interpreted as momentum such that 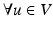 ,
, 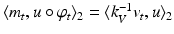 , and
, and 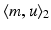 denotes the
denotes the 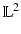 inner product between m and u, With a slight abuse of symbols, it is the result of the natural pairing between m and v in cases where m is singular (e.g., a measure). This identity is classically written as
inner product between m and u, With a slight abuse of symbols, it is the result of the natural pairing between m and v in cases where m is singular (e.g., a measure). This identity is classically written as 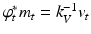 , where
, where 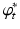 is referred to as the pullback operation on a vector measure,
is referred to as the pullback operation on a vector measure, 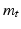 . Using the identity
. Using the identity 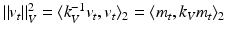 and the fact that energy-minimizing curves coincide with constant-speed length-minimizing curves, we obtain the metric distance between the atlas and target,
and the fact that energy-minimizing curves coincide with constant-speed length-minimizing curves, we obtain the metric distance between the atlas and target, 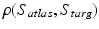 , by minimizing
, by minimizing 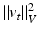 , such that
, such that 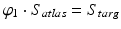 at time
at time 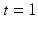 [5]. We associate this with the variational problem in the form of
[5]. We associate this with the variational problem in the form of
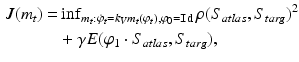
where E is defined based vector-valued measure as introduced in [18]. For any two surfaces 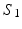 and
and 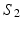 ,
, 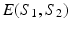 is defined as
is defined as
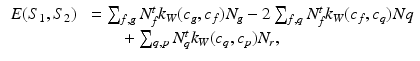
where f, g are simplices from 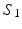 while q, p are simplices from
while q, p are simplices from 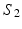 .
. 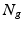 is then the normal vector pointing out of the centre,
is then the normal vector pointing out of the centre, 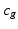 , of simplex g.
, of simplex g. 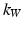 is a Gaussian kernel with bandwidth
is a Gaussian kernel with bandwidth 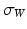 . The metric distance
. The metric distance 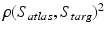 could be easily computed as
could be easily computed as 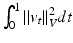 .
.
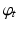 , which are solutions of ordinary differential equations
, which are solutions of ordinary differential equations ![$$\dot{\varphi }_t = v_t (\varphi _t), t \in [0,1],$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq42.gif) starting from the identity map
starting from the identity map 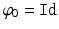 . They are therefore characterized by time-dependent velocity vector fields
. They are therefore characterized by time-dependent velocity vector fields ![$$v_t, t \in [0,1]$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq44.gif) . We define a metric distance between a target surface
. We define a metric distance between a target surface 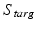 and an atlas surface
and an atlas surface 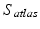 as the minimal length of curves
as the minimal length of curves ![$$\varphi _t \cdot S_{atlas}, t \in [0,1],$$](/wp-content/uploads/2016/09/A339424_1_En_24_Chapter_IEq47.gif) in a shape space such that, at time
in a shape space such that, at time 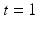 ,
, 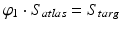 . Lengths of such curves are computed as the integrated norm
. Lengths of such curves are computed as the integrated norm 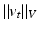 of the vector field, where
of the vector field, where 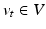 and V is a reproducing kernel Hilbert space with kernel
and V is a reproducing kernel Hilbert space with kernel 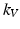 and norm
and norm 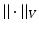 . To ensure solutions are diffeomorphisms, V must be a space of smooth vector fields. The duality isometry in Hilbert spaces allows us to express the lengths in terms of
. To ensure solutions are diffeomorphisms, V must be a space of smooth vector fields. The duality isometry in Hilbert spaces allows us to express the lengths in terms of 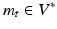 , interpreted as momentum such that
, interpreted as momentum such that 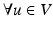 ,
, 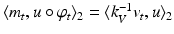 , and
, and 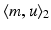 denotes the
denotes the 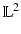 inner product between m and u, With a slight abuse of symbols, it is the result of the natural pairing between m and v in cases where m is singular (e.g., a measure). This identity is classically written as
inner product between m and u, With a slight abuse of symbols, it is the result of the natural pairing between m and v in cases where m is singular (e.g., a measure). This identity is classically written as 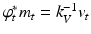 , where
, where 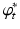 is referred to as the pullback operation on a vector measure,
is referred to as the pullback operation on a vector measure, 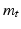 . Using the identity
. Using the identity 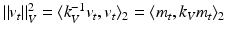 and the fact that energy-minimizing curves coincide with constant-speed length-minimizing curves, we obtain the metric distance between the atlas and target,
and the fact that energy-minimizing curves coincide with constant-speed length-minimizing curves, we obtain the metric distance between the atlas and target, 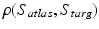 , by minimizing
, by minimizing 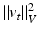 , such that
, such that 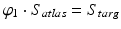 at time
at time 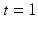 [5]. We associate this with the variational problem in the form of
[5]. We associate this with the variational problem in the form of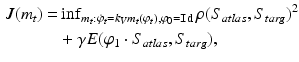
(7)
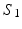 and
and 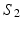 ,
, 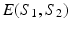 is defined as
is defined as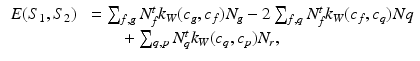
(8)
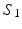 while q, p are simplices from
while q, p are simplices from 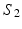 .
. 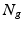 is then the normal vector pointing out of the centre,
is then the normal vector pointing out of the centre, 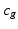 , of simplex g.
, of simplex g. 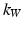 is a Gaussian kernel with bandwidth
is a Gaussian kernel with bandwidth 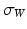 . The metric distance
. The metric distance 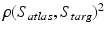 could be easily computed as
could be easily computed as 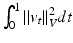 .
.We now construct the multiresolution diffeomorphic mapping for surfaces under the framework of LDDMM. In the previous section, we show that a surface, S, may be sequentially subsampled into meshes of decreasing resolution 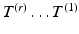 . With a slight abuse of notation, let us define these meshes as the discretization of the surface, rewriting
. With a slight abuse of notation, let us define these meshes as the discretization of the surface, rewriting 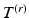 as
as 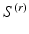 , such that
, such that 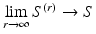 . The duality isometry of
. The duality isometry of 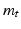 with
with 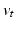 allows defining the smooth vector field,
allows defining the smooth vector field, 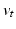 through
through 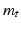 , where
, where 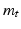 can sparsely anchor at the vertices on
can sparsely anchor at the vertices on 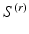 . Therefore, it is natural to seek
. Therefore, it is natural to seek 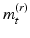 defined at the vertices on
defined at the vertices on 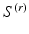 and then construct the smooth vector field,
and then construct the smooth vector field, 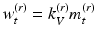 , where the size of
, where the size of 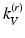 can be adapted to the sparse level of the vertices on
can be adapted to the sparse level of the vertices on 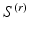 . From this construction,
. From this construction, 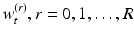 can be defined via momentum
can be defined via momentum 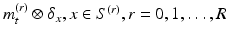 and construct independent tangent spaces of diffeomorphisms,
and construct independent tangent spaces of diffeomorphisms, 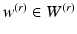 . The family of vector fields forms reproducing kernel Hilbert spaces, which could be summed across multiple resolutions, i.e.,
. The family of vector fields forms reproducing kernel Hilbert spaces, which could be summed across multiple resolutions, i.e., 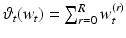 , to form one single vector field for the flow equation
, to form one single vector field for the flow equation 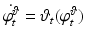 . Through this family of vector fields, we redefine
. Through this family of vector fields, we redefine 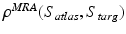 by minimizing
by minimizing 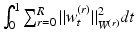 such that
such that 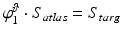 at time
at time 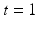 , where
, where 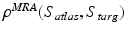 is in turn similar to that proposed for the large deformation diffeomorphic kernel bundle mapping (LDDKBM) for the registration of images [16].
is in turn similar to that proposed for the large deformation diffeomorphic kernel bundle mapping (LDDKBM) for the registration of images [16].
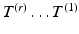 . With a slight abuse of notation, let us define these meshes as the discretization of the surface, rewriting
. With a slight abuse of notation, let us define these meshes as the discretization of the surface, rewriting 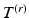 as
as 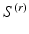 , such that
, such that 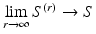 . The duality isometry of
. The duality isometry of 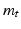 with
with 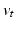 allows defining the smooth vector field,
allows defining the smooth vector field, 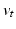 through
through 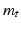 , where
, where 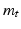 can sparsely anchor at the vertices on
can sparsely anchor at the vertices on 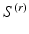 . Therefore, it is natural to seek
. Therefore, it is natural to seek 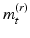 defined at the vertices on
defined at the vertices on 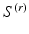 and then construct the smooth vector field,
and then construct the smooth vector field, 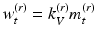 , where the size of
, where the size of 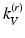 can be adapted to the sparse level of the vertices on
can be adapted to the sparse level of the vertices on 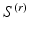 . From this construction,
. From this construction, 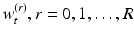 can be defined via momentum
can be defined via momentum 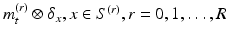 and construct independent tangent spaces of diffeomorphisms,
and construct independent tangent spaces of diffeomorphisms, 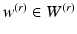 . The family of vector fields forms reproducing kernel Hilbert spaces, which could be summed across multiple resolutions, i.e.,
. The family of vector fields forms reproducing kernel Hilbert spaces, which could be summed across multiple resolutions, i.e., 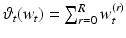 , to form one single vector field for the flow equation
, to form one single vector field for the flow equation 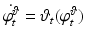 . Through this family of vector fields, we redefine
. Through this family of vector fields, we redefine 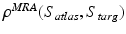 by minimizing
by minimizing 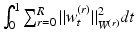 such that
such that 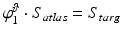 at time
at time 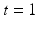 , where
, where 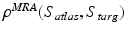 is in turn similar to that proposed for the large deformation diffeomorphic kernel bundle mapping (LDDKBM) for the registration of images [16].
is in turn similar to that proposed for the large deformation diffeomorphic kernel bundle mapping (LDDKBM) for the registration of images [16].Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




