Fig. 1.
(a) The sphere 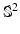 and optimal paths for different costs: (black curve) a geodesic between the north pole and a point on the southern hemisphere; (blue curve) a most probable path (MPP) between the points for an anisotropic diffusion starting at the north pole with covariance
and optimal paths for different costs: (black curve) a geodesic between the north pole and a point on the southern hemisphere; (blue curve) a most probable path (MPP) between the points for an anisotropic diffusion starting at the north pole with covariance 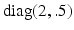 as indicated by the horizontal ellipsis at the north pole. The covariance is proportional to the squared length of the vectors that constitute a frame for
as indicated by the horizontal ellipsis at the north pole. The covariance is proportional to the squared length of the vectors that constitute a frame for 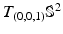 . The frame is parallel transported along the MPP (arrows). The MPP increases the movement in the direction of minor variance as it reaches the southern hemisphere. Compare with Fig. 2 (a,b). (b) Frame bundle diffusion: for each
. The frame is parallel transported along the MPP (arrows). The MPP increases the movement in the direction of minor variance as it reaches the southern hemisphere. Compare with Fig. 2 (a,b). (b) Frame bundle diffusion: for each 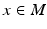 , the fibers (black arrows) contain frames
, the fibers (black arrows) contain frames 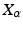 for
for 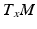 . The stochastic paths from x (blue) transport the initial frame
. The stochastic paths from x (blue) transport the initial frame 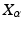 (red vectors) horizontally in the frame bundle by parallel transport (green curves and vectors). The map
(red vectors) horizontally in the frame bundle by parallel transport (green curves and vectors). The map 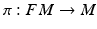 sends a point and frame
sends a point and frame 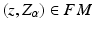 to the base point
to the base point 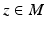 (Color figure online).
(Color figure online).
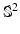 and optimal paths for different costs: (black curve) a geodesic between the north pole and a point on the southern hemisphere; (blue curve) a most probable path (MPP) between the points for an anisotropic diffusion starting at the north pole with covariance
and optimal paths for different costs: (black curve) a geodesic between the north pole and a point on the southern hemisphere; (blue curve) a most probable path (MPP) between the points for an anisotropic diffusion starting at the north pole with covariance 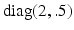 as indicated by the horizontal ellipsis at the north pole. The covariance is proportional to the squared length of the vectors that constitute a frame for
as indicated by the horizontal ellipsis at the north pole. The covariance is proportional to the squared length of the vectors that constitute a frame for 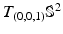 . The frame is parallel transported along the MPP (arrows). The MPP increases the movement in the direction of minor variance as it reaches the southern hemisphere. Compare with Fig. 2 (a,b). (b) Frame bundle diffusion: for each
. The frame is parallel transported along the MPP (arrows). The MPP increases the movement in the direction of minor variance as it reaches the southern hemisphere. Compare with Fig. 2 (a,b). (b) Frame bundle diffusion: for each 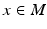 , the fibers (black arrows) contain frames
, the fibers (black arrows) contain frames 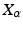 for
for 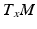 . The stochastic paths from x (blue) transport the initial frame
. The stochastic paths from x (blue) transport the initial frame 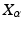 (red vectors) horizontally in the frame bundle by parallel transport (green curves and vectors). The map
(red vectors) horizontally in the frame bundle by parallel transport (green curves and vectors). The map 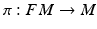 sends a point and frame
sends a point and frame 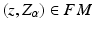 to the base point
to the base point 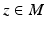 (Color figure online).
(Color figure online).1.1 Content and Outline
We construct an intrinsic statistical approach to modeling anisotropic data in manifolds using diffusions processes. We describe how the Eells-Elworthy-Malliavin construction of Brownian motion defines a space of probability distributions and how the non-linear template estimation problem can be recast using this construction. We argue for why the most probable paths are more natural than geodesics for representing data under the model and for approximating likelihood, and we derive analytical expressions for the flow equations by identifying the paths as projections of extremal curves on a sub-Riemannian manifold. The paper ends with numerical experiments on the sphere for visualization and further on the LDDMM manifold of landmarks that is widely used in medical imaging and computational anatomy.
The paper thus presents an entirely new approach to one of the most import tasks in medical imaging: template and covariance estimation. The focus is on the theoretical insight behind the construction. The experiments presented indicate the effect of the new model without attempting to constitute a thorough evaluation on medical data. We will explore that further in future work.
While the paper necessarily uses differential geometry, we seek to only include technical details strictly needed for the exposition. Likewise, in order to clearly express the differential geometric ideas, analytical details of stochastic differential equations will be omitted.
2 Background
The data observed in a range of medical imaging applications can only be properly modeled in nonlinear spaces. Differentiable manifolds are therefore used for shape models from the Kendall shape spaces [8], to embedded curves [11] and m-reps and related models [15]. In computational anatomy, the LDDMM framework [23] provides a range of nonlinear geometries dependent on the data types to be matched: landmarks, curves, surfaces, images and tensors lead to different manifolds.
The goal of template estimation is to find a representative for a population of observations [6], for example as a Fréchet mean. Template estimation can be considered a non-linear generalization of the Euclidean space mean estimation. The Principal Geodesic Analysis (PGA, [2]) goes beyond the mean or template by modeling the covariance structure and linearizing data to the tangent space of the mean. Geodesic PCA (GPCA, [5]) and Horizontal Component Analysis (HCA, [16]) likewise provide low dimensional models of manifold valued data by seeking to generalize the Euclidean principal component analysis procedure. Probabilistic PGA [24] builds a latent variable model similar to [20] by the geodesic spray of linearly transformed latent variables. Generalizing Euclidean statistical tools to properly handling curved geometries [14] remain a challenging problem.
The frame bundle was used for dimensionality reduction with HCA [16] and later for Diffusion PCA (DPCA, [17]). While the current paper builds a statistical model similar to the DPCA construction, the focus is on the influence of anisotropy, in particular on the optimal curves, and on likelihood approximation.
For template estimation [6] and first order models such as [21], geodesic curves play a fundamental role. The Fréchet mean minimizes squared geodesic distances, and the momentum representation in the Lie algebra, the tangent space at identity, uses momenta or velocity vectors as representatives of the observed samples. Geodesics and geodesic distances take the role of difference vectors and norms in Euclidean space because differences between the template and the observed data cannot be represented by vectors in the nonlinear geometry. Geodesic paths are used because they are locally length minimizing. The fundamental argument in this paper is that in the case of anisotropy, a different family of curves and distance metrics can be used: the most probable paths for anisotropic distributions and log-likelihoods, respectively.
3 A Class of Anisotropic Distributions
In Euclidean space, the normal distribution 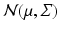 can be defined as the transition probability of a driftless diffusion process with stationary generator
can be defined as the transition probability of a driftless diffusion process with stationary generator 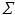 stopped at time
stopped at time 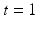 , i.e. as the solution of the stochastic differential equation
, i.e. as the solution of the stochastic differential equation 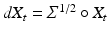 . Here, the probability density
. Here, the probability density 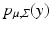 is given by the marginal density of all sample paths ending at y. Formally,
is given by the marginal density of all sample paths ending at y. Formally, 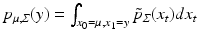 where the path density
where the path density 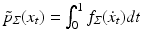 integrates the density of a normal distribution
integrates the density of a normal distribution 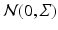 on the infinitesimal steps
on the infinitesimal steps 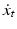 .1
.1
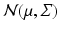 can be defined as the transition probability of a driftless diffusion process with stationary generator
can be defined as the transition probability of a driftless diffusion process with stationary generator 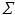 stopped at time
stopped at time 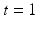 , i.e. as the solution of the stochastic differential equation
, i.e. as the solution of the stochastic differential equation 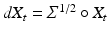 . Here, the probability density
. Here, the probability density 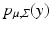 is given by the marginal density of all sample paths ending at y. Formally,
is given by the marginal density of all sample paths ending at y. Formally, 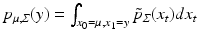 where the path density
where the path density 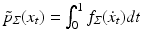 integrates the density of a normal distribution
integrates the density of a normal distribution 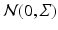 on the infinitesimal steps
on the infinitesimal steps 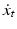 .1
.1 In the Euclidean case, the distribution of 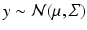 can equivalently be specified both using the difference vector
can equivalently be specified both using the difference vector 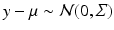 between observations and mean and using the density
between observations and mean and using the density 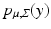 that comes from the path density
that comes from the path density 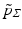 as above. The latter definition is however much more amenable to the nonlinear situation where a displacement vector
as above. The latter definition is however much more amenable to the nonlinear situation where a displacement vector 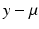 does not have intrinsic meaning. In a differentiable manifold M, vector space structure is lost but infinitesimal displacements remain in the form of tangent vectors in the tangent spaces
does not have intrinsic meaning. In a differentiable manifold M, vector space structure is lost but infinitesimal displacements remain in the form of tangent vectors in the tangent spaces 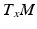 ,
, 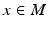 . The path density
. The path density 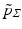 therefore allows a more natural generalization to the nonlinear situation.
therefore allows a more natural generalization to the nonlinear situation.
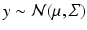 can equivalently be specified both using the difference vector
can equivalently be specified both using the difference vector 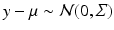 between observations and mean and using the density
between observations and mean and using the density 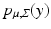 that comes from the path density
that comes from the path density 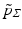 as above. The latter definition is however much more amenable to the nonlinear situation where a displacement vector
as above. The latter definition is however much more amenable to the nonlinear situation where a displacement vector 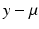 does not have intrinsic meaning. In a differentiable manifold M, vector space structure is lost but infinitesimal displacements remain in the form of tangent vectors in the tangent spaces
does not have intrinsic meaning. In a differentiable manifold M, vector space structure is lost but infinitesimal displacements remain in the form of tangent vectors in the tangent spaces 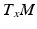 ,
, 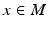 . The path density
. The path density 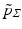 therefore allows a more natural generalization to the nonlinear situation.
therefore allows a more natural generalization to the nonlinear situation.We here outline a construction of anisotropic normal distributions using diffusion processes. We present the discussion in the continuous limit omitting the stochastic analysis needed when the time steps of the stochastic paths goes to zero.
3.1 Stochastic Diffusion Processes on Manifolds
Let M be a manifold with affine connection 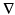 , and possibly Riemannian metric g. Isotropic diffusions can then be constructed as eigenfunctions of the Laplace-Beltrami operator. The Eells-Elworthy-Malliavin construction of Brownian motion (see e.g. [4]) provides an equivalent construction2 that also extends to anisotropic diffusions. The starting point is the frame bundle FM that consists of pairs
, and possibly Riemannian metric g. Isotropic diffusions can then be constructed as eigenfunctions of the Laplace-Beltrami operator. The Eells-Elworthy-Malliavin construction of Brownian motion (see e.g. [4]) provides an equivalent construction2 that also extends to anisotropic diffusions. The starting point is the frame bundle FM that consists of pairs 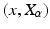 of points
of points 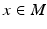 and frames
and frames 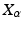 at x. A frame at x is a collection of
at x. A frame at x is a collection of 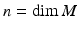 tangent vectors in
tangent vectors in 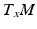 that together constitute a basis for the tangent space. The frame can thereby be considered an invertible linear map
that together constitute a basis for the tangent space. The frame can thereby be considered an invertible linear map 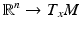 . If
. If 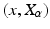 is a point in FM, the frame
is a point in FM, the frame 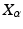 can be considered a representation of the square root covariance matrix
can be considered a representation of the square root covariance matrix 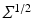 that we used above and thus a representation for a diffusion process starting at x. The frame being invertible implies that the square root covariance has full rank.
that we used above and thus a representation for a diffusion process starting at x. The frame being invertible implies that the square root covariance has full rank.
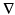 , and possibly Riemannian metric g. Isotropic diffusions can then be constructed as eigenfunctions of the Laplace-Beltrami operator. The Eells-Elworthy-Malliavin construction of Brownian motion (see e.g. [4]) provides an equivalent construction2 that also extends to anisotropic diffusions. The starting point is the frame bundle FM that consists of pairs
, and possibly Riemannian metric g. Isotropic diffusions can then be constructed as eigenfunctions of the Laplace-Beltrami operator. The Eells-Elworthy-Malliavin construction of Brownian motion (see e.g. [4]) provides an equivalent construction2 that also extends to anisotropic diffusions. The starting point is the frame bundle FM that consists of pairs 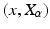 of points
of points 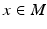 and frames
and frames 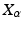 at x. A frame at x is a collection of
at x. A frame at x is a collection of 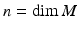 tangent vectors in
tangent vectors in 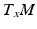 that together constitute a basis for the tangent space. The frame can thereby be considered an invertible linear map
that together constitute a basis for the tangent space. The frame can thereby be considered an invertible linear map 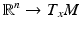 . If
. If 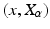 is a point in FM, the frame
is a point in FM, the frame 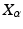 can be considered a representation of the square root covariance matrix
can be considered a representation of the square root covariance matrix 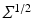 that we used above and thus a representation for a diffusion process starting at x. The frame being invertible implies that the square root covariance has full rank.
that we used above and thus a representation for a diffusion process starting at x. The frame being invertible implies that the square root covariance has full rank.The difficulty in defining a diffusion process from 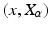 lies in the fact that the frame
lies in the fact that the frame 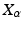 cannot in general be defined globally on the manifold. A frame
cannot in general be defined globally on the manifold. A frame 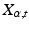 can however be defined at a point
can however be defined at a point 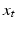 close to x by parallel transport along a curve from x to
close to x by parallel transport along a curve from x to 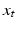 . It is a fundamental property of curvature denoted holonomy [10] that this transport depends on the chosen curve, and the transport is therefore not unique. The Eells-Elworthy-Malliavin construction handles this by constructing the diffusion in FM directly so that each stochastic path carries with it the frame by parallel transport. If
. It is a fundamental property of curvature denoted holonomy [10] that this transport depends on the chosen curve, and the transport is therefore not unique. The Eells-Elworthy-Malliavin construction handles this by constructing the diffusion in FM directly so that each stochastic path carries with it the frame by parallel transport. If 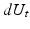 is a solution to such a diffusion in FM,
is a solution to such a diffusion in FM, 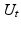 projects to a process
projects to a process 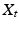 in M by the projection
in M by the projection 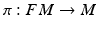 that maps
that maps 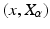 to the base point x. Different paths reaching x hit different elements of the fiber
to the base point x. Different paths reaching x hit different elements of the fiber 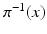 due to the holonomy, and the projection thus essentially integrates out the holonomy. The solutions at
due to the holonomy, and the projection thus essentially integrates out the holonomy. The solutions at 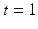 which we will use are stochastic variables, and we write
which we will use are stochastic variables, and we write 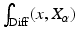 for the map from initial conditions to
for the map from initial conditions to 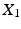 . If M has a volume form, the stochastic variable
. If M has a volume form, the stochastic variable 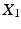 has a density which generalizes the Euclidean density
has a density which generalizes the Euclidean density 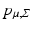 above.
above.
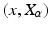 lies in the fact that the frame
lies in the fact that the frame 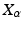 cannot in general be defined globally on the manifold. A frame
cannot in general be defined globally on the manifold. A frame 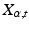 can however be defined at a point
can however be defined at a point 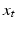 close to x by parallel transport along a curve from x to
close to x by parallel transport along a curve from x to 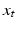 . It is a fundamental property of curvature denoted holonomy [10] that this transport depends on the chosen curve, and the transport is therefore not unique. The Eells-Elworthy-Malliavin construction handles this by constructing the diffusion in FM directly so that each stochastic path carries with it the frame by parallel transport. If
. It is a fundamental property of curvature denoted holonomy [10] that this transport depends on the chosen curve, and the transport is therefore not unique. The Eells-Elworthy-Malliavin construction handles this by constructing the diffusion in FM directly so that each stochastic path carries with it the frame by parallel transport. If 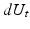 is a solution to such a diffusion in FM,
is a solution to such a diffusion in FM, 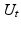 projects to a process
projects to a process 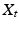 in M by the projection
in M by the projection 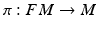 that maps
that maps 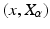 to the base point x. Different paths reaching x hit different elements of the fiber
to the base point x. Different paths reaching x hit different elements of the fiber 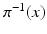 due to the holonomy, and the projection thus essentially integrates out the holonomy. The solutions at
due to the holonomy, and the projection thus essentially integrates out the holonomy. The solutions at 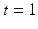 which we will use are stochastic variables, and we write
which we will use are stochastic variables, and we write 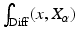 for the map from initial conditions to
for the map from initial conditions to 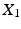 . If M has a volume form, the stochastic variable
. If M has a volume form, the stochastic variable 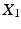 has a density which generalizes the Euclidean density
has a density which generalizes the Euclidean density 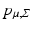 above.
above.3.2 Parallel Transport and Horizontallity
The parallel transport of a frame 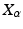 from x to a frame
from x to a frame 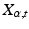 on
on 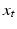 defines a map from curves
defines a map from curves 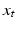 on M to curves
on M to curves 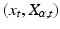 in FM called a horizontal lift. The tangent vectors of lifted curves
in FM called a horizontal lift. The tangent vectors of lifted curves 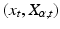 define a subspace of the frame bundle tangent space
define a subspace of the frame bundle tangent space 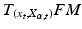 that is denoted the horizontal subspace
that is denoted the horizontal subspace 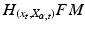 . This space of dimension n is naturally isomorphic to
. This space of dimension n is naturally isomorphic to 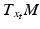 by the map
by the map 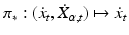 and it is spanned by n vector fields
and it is spanned by n vector fields 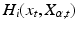 called horizontal vector fields. Using the horizontal vector fields, the FM diffusion
called horizontal vector fields. Using the horizontal vector fields, the FM diffusion 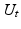 is defined by the SDE
is defined by the SDE
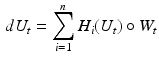
where 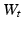 is an
is an 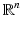 valued Wiener process. The diffusion thereby only flows in the horizontal part of the frame bundle, see Fig. 1 (b). Note that if M is Euclidean, the solution
valued Wiener process. The diffusion thereby only flows in the horizontal part of the frame bundle, see Fig. 1 (b). Note that if M is Euclidean, the solution 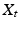 is a stationary diffusion process.
is a stationary diffusion process.
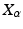 from x to a frame
from x to a frame 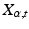 on
on 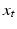 defines a map from curves
defines a map from curves 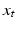 on M to curves
on M to curves 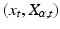 in FM called a horizontal lift. The tangent vectors of lifted curves
in FM called a horizontal lift. The tangent vectors of lifted curves 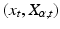 define a subspace of the frame bundle tangent space
define a subspace of the frame bundle tangent space 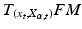 that is denoted the horizontal subspace
that is denoted the horizontal subspace 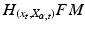 . This space of dimension n is naturally isomorphic to
. This space of dimension n is naturally isomorphic to 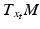 by the map
by the map 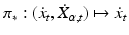 and it is spanned by n vector fields
and it is spanned by n vector fields 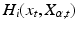 called horizontal vector fields. Using the horizontal vector fields, the FM diffusion
called horizontal vector fields. Using the horizontal vector fields, the FM diffusion 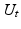 is defined by the SDE
is defined by the SDE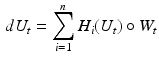
(1)
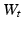 is an
is an 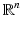 valued Wiener process. The diffusion thereby only flows in the horizontal part of the frame bundle, see Fig. 1 (b). Note that if M is Euclidean, the solution
valued Wiener process. The diffusion thereby only flows in the horizontal part of the frame bundle, see Fig. 1 (b). Note that if M is Euclidean, the solution 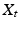 is a stationary diffusion process.
is a stationary diffusion process.This way of linking curves and transport of frames is also denoted “rolling without slipping” [4]. The procedure is defined only using the connection 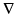 and its parallel transport. A Riemannian metric is therefore not needed at this point (though a Riemannian metric can be used to define a connection). A volume form on M, for example induced by a Riemannian metric, is however needed when we use densities for likelihoods later.
and its parallel transport. A Riemannian metric is therefore not needed at this point (though a Riemannian metric can be used to define a connection). A volume form on M, for example induced by a Riemannian metric, is however needed when we use densities for likelihoods later.
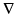 and its parallel transport. A Riemannian metric is therefore not needed at this point (though a Riemannian metric can be used to define a connection). A volume form on M, for example induced by a Riemannian metric, is however needed when we use densities for likelihoods later.
and its parallel transport. A Riemannian metric is therefore not needed at this point (though a Riemannian metric can be used to define a connection). A volume form on M, for example induced by a Riemannian metric, is however needed when we use densities for likelihoods later.3.3 Why Parallel Transport?
In Euclidean space, the matrix 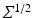 being the square root of the covariance matrix specifies the diffusion process. In the manifold situation, the frame
being the square root of the covariance matrix specifies the diffusion process. In the manifold situation, the frame 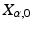 takes the place of
takes the place of 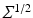 by specifying the covariance of infinitesimal steps. The parallel transport provides a way of linking tangent spaces, and it therefore links the covariance at
by specifying the covariance of infinitesimal steps. The parallel transport provides a way of linking tangent spaces, and it therefore links the covariance at 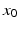 with the covariance at
with the covariance at 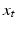 . Since the acceleration
. Since the acceleration 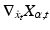 vanishes when
vanishes when 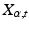 is parallel transported, this can be interpreted as a transport of covariance between two tangent spaces with no change seen from the manifold, i.e. no change measured by the connection
is parallel transported, this can be interpreted as a transport of covariance between two tangent spaces with no change seen from the manifold, i.e. no change measured by the connection 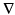 . While
. While 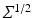 can be defined globally in Euclidean space, each sample path will here carry its own transport of
can be defined globally in Euclidean space, each sample path will here carry its own transport of 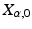 , and two paths ending at
, and two paths ending at 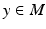 will generally transport the covariance differently. The global effect of this stochastic holonomy can seem quite counterintuitive when related to the Euclidean situation but the infinitesimal effect is natural as a transport with no change seen from
will generally transport the covariance differently. The global effect of this stochastic holonomy can seem quite counterintuitive when related to the Euclidean situation but the infinitesimal effect is natural as a transport with no change seen from 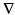 .
.
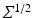 being the square root of the covariance matrix specifies the diffusion process. In the manifold situation, the frame
being the square root of the covariance matrix specifies the diffusion process. In the manifold situation, the frame 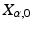 takes the place of
takes the place of 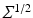 by specifying the covariance of infinitesimal steps. The parallel transport provides a way of linking tangent spaces, and it therefore links the covariance at
by specifying the covariance of infinitesimal steps. The parallel transport provides a way of linking tangent spaces, and it therefore links the covariance at 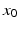 with the covariance at
with the covariance at 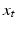 . Since the acceleration
. Since the acceleration 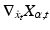 vanishes when
vanishes when 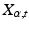 is parallel transported, this can be interpreted as a transport of covariance between two tangent spaces with no change seen from the manifold, i.e. no change measured by the connection
is parallel transported, this can be interpreted as a transport of covariance between two tangent spaces with no change seen from the manifold, i.e. no change measured by the connection 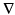 . While
. While 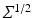 can be defined globally in Euclidean space, each sample path will here carry its own transport of
can be defined globally in Euclidean space, each sample path will here carry its own transport of 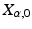 , and two paths ending at
, and two paths ending at 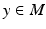 will generally transport the covariance differently. The global effect of this stochastic holonomy can seem quite counterintuitive when related to the Euclidean situation but the infinitesimal effect is natural as a transport with no change seen from
will generally transport the covariance differently. The global effect of this stochastic holonomy can seem quite counterintuitive when related to the Euclidean situation but the infinitesimal effect is natural as a transport with no change seen from 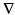 .
.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




