denote a data matrix
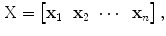
(1)
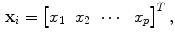
(2)
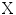 contains
contains 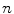 measurements of
measurements of 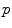 variables. Compute the covariance matrix
variables. Compute the covariance matrix 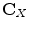 as
as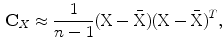
(3)
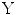 .
.For PCA, a linear transform 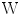 is estimated such that the variance of the components of
is estimated such that the variance of the components of 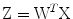 is maximized under the constraint that the components
is maximized under the constraint that the components 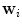 of
of 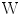 are orthogonal, i.e. the components of
are orthogonal, i.e. the components of 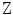 are uncorrelated and
are uncorrelated and 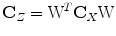 is diagonal. In CCA, two linear transforms,
is diagonal. In CCA, two linear transforms, 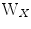 and
and 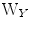 , are estimated such that the correlation
, are estimated such that the correlation 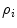 between the reduced variables (canonical variates) of
between the reduced variables (canonical variates) of 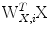 and
and 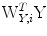 , have been maximized and that the different components of
, have been maximized and that the different components of 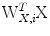 and
and 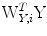 are uncorrelated with respect to each other. Note that for CCA, the data matrices
are uncorrelated with respect to each other. Note that for CCA, the data matrices 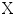 and
and 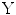 are not required to have the same number of variables, therefore the number of canonical variates will correspond to the smallest number of variables provided by either
are not required to have the same number of variables, therefore the number of canonical variates will correspond to the smallest number of variables provided by either 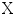 or
or 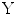 . Estimating the linear transforms
. Estimating the linear transforms 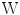 in PCA, and
in PCA, and 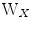 and
and 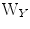 in CCA are done solving an eigenvector problem, hence, the term eigenspine.
in CCA are done solving an eigenvector problem, hence, the term eigenspine.
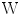 is estimated such that the variance of the components of
is estimated such that the variance of the components of 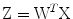 is maximized under the constraint that the components
is maximized under the constraint that the components 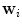 of
of 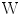 are orthogonal, i.e. the components of
are orthogonal, i.e. the components of 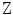 are uncorrelated and
are uncorrelated and 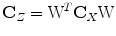 is diagonal. In CCA, two linear transforms,
is diagonal. In CCA, two linear transforms, 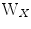 and
and 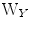 , are estimated such that the correlation
, are estimated such that the correlation 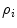 between the reduced variables (canonical variates) of
between the reduced variables (canonical variates) of 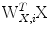 and
and 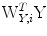 , have been maximized and that the different components of
, have been maximized and that the different components of 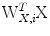 and
and 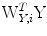 are uncorrelated with respect to each other. Note that for CCA, the data matrices
are uncorrelated with respect to each other. Note that for CCA, the data matrices 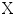 and
and 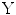 are not required to have the same number of variables, therefore the number of canonical variates will correspond to the smallest number of variables provided by either
are not required to have the same number of variables, therefore the number of canonical variates will correspond to the smallest number of variables provided by either 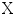 or
or 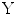 . Estimating the linear transforms
. Estimating the linear transforms 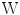 in PCA, and
in PCA, and 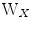 and
and 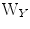 in CCA are done solving an eigenvector problem, hence, the term eigenspine.
in CCA are done solving an eigenvector problem, hence, the term eigenspine.An interesting aspect of CCA is its relation with mutual information (MI). As shown by [9], the mutual information between 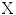 and
and 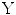 can be estimated as the sum of the mutual information of the reduced variables, given that their statistical dependence is limited to correlation. For normally distributed variables, this relation is given as
can be estimated as the sum of the mutual information of the reduced variables, given that their statistical dependence is limited to correlation. For normally distributed variables, this relation is given as
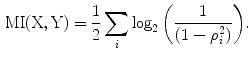
This follows from considering a continuous random variable 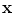 with the differential entropy defined as
with the differential entropy defined as
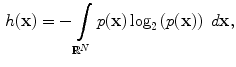
where 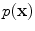 is the probability density function of
is the probability density function of 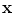 . Consider similarly a continuous random variable
. Consider similarly a continuous random variable 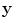 , then it can be shown that
, then it can be shown that
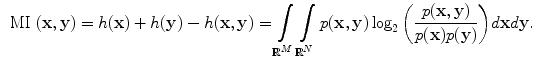
Further, consider a Gaussian distributed variable 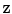 , for which the differential entropy is given as
, for which the differential entropy is given as
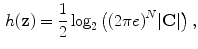
where 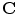 is the covariance matrix of
is the covariance matrix of 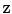 . In the case of two
. In the case of two 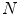 -dimensional variables, then (6) becomes
-dimensional variables, then (6) becomes
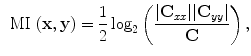
where
![$$\begin{aligned} \mathbf {C} = \left[ \begin{matrix}{{\mathbf {C}}_{xx}} &{} {\mathbf {{{C}}}_{xy}}\\ {\mathbf {{{C}}}_{yx}} &{}{\mathbf {{{C}}}_{yy}}\end{matrix}\right] . \end{aligned}$$](/wp-content/uploads/2016/03/A323246_1_En_11_Chapter_Equ9.gif)
For two one-dimensional Gaussian distributed variables, (8) reduces to
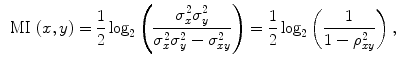
where 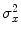 and
and 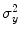 are the variances of
are the variances of 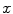 and
and 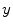 ,
, 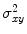 is the covariance of
is the covariance of 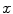 and
and 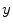 and
and 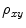 is the correlation between
is the correlation between 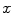 and
and 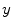 . Given that information is additive, for statistically independent variables, and that the canonical variates are uncorrelated, i.e.
. Given that information is additive, for statistically independent variables, and that the canonical variates are uncorrelated, i.e. 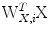 and
and 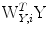 , hence, the mutual information between
, hence, the mutual information between 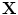 and
and 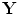 is the sum of the mutual information between the variates.
is the sum of the mutual information between the variates.
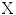 and
and 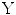 can be estimated as the sum of the mutual information of the reduced variables, given that their statistical dependence is limited to correlation. For normally distributed variables, this relation is given as
can be estimated as the sum of the mutual information of the reduced variables, given that their statistical dependence is limited to correlation. For normally distributed variables, this relation is given as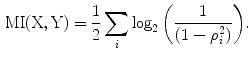
(4)
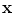 with the differential entropy defined as
with the differential entropy defined as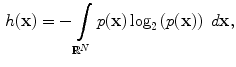
(5)
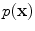 is the probability density function of
is the probability density function of 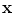 . Consider similarly a continuous random variable
. Consider similarly a continuous random variable 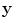 , then it can be shown that
, then it can be shown that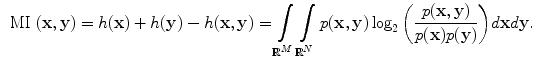
(6)
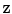 , for which the differential entropy is given as
, for which the differential entropy is given as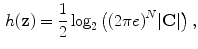
(7)
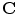 is the covariance matrix of
is the covariance matrix of 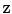 . In the case of two
. In the case of two 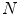 -dimensional variables, then (6) becomes
-dimensional variables, then (6) becomes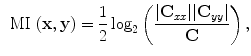
(8)
![$$\begin{aligned} \mathbf {C} = \left[ \begin{matrix}{{\mathbf {C}}_{xx}} &{} {\mathbf {{{C}}}_{xy}}\\ {\mathbf {{{C}}}_{yx}} &{}{\mathbf {{{C}}}_{yy}}\end{matrix}\right] . \end{aligned}$$](/wp-content/uploads/2016/03/A323246_1_En_11_Chapter_Equ9.gif)
(9)
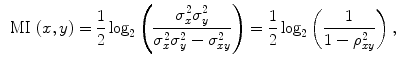
(10)
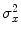 and
and 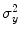 are the variances of
are the variances of 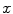 and
and 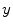 ,
, 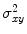 is the covariance of
is the covariance of 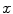 and
and 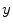 and
and 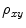 is the correlation between
is the correlation between 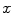 and
and 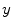 . Given that information is additive, for statistically independent variables, and that the canonical variates are uncorrelated, i.e.
. Given that information is additive, for statistically independent variables, and that the canonical variates are uncorrelated, i.e. 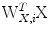 and
and 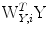 , hence, the mutual information between
, hence, the mutual information between 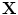 and
and 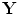 is the sum of the mutual information between the variates.
is the sum of the mutual information between the variates.Note that using the 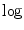 -function with the base
-function with the base 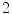 provides an MI measure defined in bits. This measure will be employed in the subsequent analysis for quantifying the dependence between different measures.
provides an MI measure defined in bits. This measure will be employed in the subsequent analysis for quantifying the dependence between different measures.
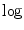 -function with the base
-function with the base 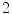 provides an MI measure defined in bits. This measure will be employed in the subsequent analysis for quantifying the dependence between different measures.
provides an MI measure defined in bits. This measure will be employed in the subsequent analysis for quantifying the dependence between different measures.3 Experiments
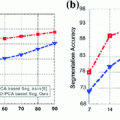
To demonstrate the use of the data analysis scheme, measurements of the position and the orientation of the vertebrae for a number of patients were analyzed to determine which of these measures that have the strongest linear dependence.
3.1 Image Data
Image data from 22 patients (19 female and three male) were retrospectively gathered and extracted from the local picture archiving and communications system. The only criteria for inclusion was that the patient suffered from idiopathic scoliosis and that the CT data had a resolution higher than 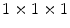 mm
mm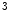 . The data sets depicted all lumbar and thoracic vertebrae, i.e. 17 vertebrae per patient. The requirement on the resolution was needed in order to be able to distinguish adjacent vertebrae in the subsequently applied method for obtaining the position and rotation of each vertebra. The patients had an average age of
. The data sets depicted all lumbar and thoracic vertebrae, i.e. 17 vertebrae per patient. The requirement on the resolution was needed in order to be able to distinguish adjacent vertebrae in the subsequently applied method for obtaining the position and rotation of each vertebra. The patients had an average age of 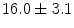 years at the time of their respective examinations and an average Cobb angle of
years at the time of their respective examinations and an average Cobb angle of 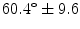 (standing position). Most patients were classified has having a scoliosis of Lenke type 3C or 4C.
(standing position). Most patients were classified has having a scoliosis of Lenke type 3C or 4C.
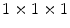 mm
mm . The data sets depicted all lumbar and thoracic vertebrae, i.e. 17 vertebrae per patient. The requirement on the resolution was needed in order to be able to distinguish adjacent vertebrae in the subsequently applied method for obtaining the position and rotation of each vertebra. The patients had an average age of
. The data sets depicted all lumbar and thoracic vertebrae, i.e. 17 vertebrae per patient. The requirement on the resolution was needed in order to be able to distinguish adjacent vertebrae in the subsequently applied method for obtaining the position and rotation of each vertebra. The patients had an average age of 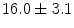 years at the time of their respective examinations and an average Cobb angle of
years at the time of their respective examinations and an average Cobb angle of 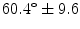 (standing position). Most patients were classified has having a scoliosis of Lenke type 3C or 4C.
(standing position). Most patients were classified has having a scoliosis of Lenke type 3C or 4C.The images were captured as a part of the standard routine for pre-operational planning and they were anonymized before being exported by clinical staff. Note that for patients of similar age as included in this retrospective study, it is often questionable whether a CT scan is appropriate or not, due to the exposure to radiation. However, at the local hospital there is a protocol in place for acquiring low-dose CT examinations with maintained image quality, targeted towards examinations of the spine. With the use of this protocol, the radiation dose is approximately 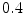 mSv. More on this can be found in [8].
mSv. More on this can be found in [8].
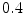 mSv. More on this can be found in [8].
mSv. More on this can be found in [8].3.2 Curvature Measures
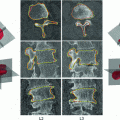
Each data set was processed with the method presented in [5], which is based on the following steps; extraction of the spinal canal centerline, disc detection, vertebra centerpoint estimation and vertebra rotation estimation. A graphical overview of the method is provided in Fig. 1. In [5], the method was shown to have a variability, when compared with manual measurements, that is on par with the inter-observer variability for measuring the axial vertebral rotation. This was supported by Bland-Altman plots and high values of the intraclass correlation coefficient, thus, showing that the method can be used as a replacement for manual measurements.
The method estimates, for each vertebra, the position ![$$ [x,y,z] $$](/wp-content/uploads/2016/03/A323246_1_En_11_Chapter_IEq58.gif) and the rotation matrix
and the rotation matrix 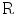 , from which the rotation angles
, from which the rotation angles ![$$[\theta _{X},\theta _{Y},\theta _{Z}]$$](/wp-content/uploads/2016/03/A323246_1_En_11_Chapter_IEq60.gif) can be derived. The rotation angles were computed as the Euler angles (using a fixed world frame) of the rotation matrix
can be derived. The rotation angles were computed as the Euler angles (using a fixed world frame) of the rotation matrix 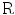 . Note the order of the rotational angles,
. Note the order of the rotational angles, 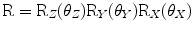 .
. 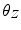 corresponds to axial vertebral rotation,
corresponds to axial vertebral rotation, 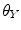 to frontal rotation and
to frontal rotation and 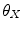




![$$ [x,y,z] $$](/wp-content/uploads/2016/03/A323246_1_En_11_Chapter_IEq58.gif) and the rotation matrix
and the rotation matrix 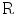 , from which the rotation angles
, from which the rotation angles ![$$[\theta _{X},\theta _{Y},\theta _{Z}]$$](/wp-content/uploads/2016/03/A323246_1_En_11_Chapter_IEq60.gif) can be derived. The rotation angles were computed as the Euler angles (using a fixed world frame) of the rotation matrix
can be derived. The rotation angles were computed as the Euler angles (using a fixed world frame) of the rotation matrix 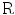 . Note the order of the rotational angles,
. Note the order of the rotational angles, 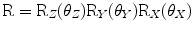 .
. 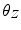 corresponds to axial vertebral rotation,
corresponds to axial vertebral rotation, 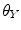 to frontal rotation and
to frontal rotation and 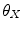
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree