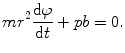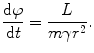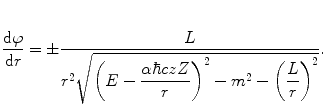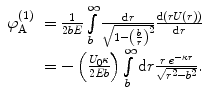(1)
Amersham, Buckinghamshire, UK
4.1 Introduction
4.2.1 Scattering Integral
4.3.1 Introduction
4.3.6 Mott Scatter
4.3.8 Spin-1 Projectile
Abstract
This chapter begins Part II of this book with an exploration of the physics of a process which will be fundamental throughout our future discussions, that of the Coulomb interaction between a moving charged particle and a stationary charged body or, equivalently, a Coulomb potential. The result is scatter, or the deviation of the moving particle from its original trajectory. Energy can be transferred through the recoil of the target. Here, the target is assumed to be a bare (unscreened) point charge. We begin with two independent classical descriptions of the problem: one based upon our development of the scattering integral and the other based upon the Laplace–Runge–Lenz vector. Both yield the same result in that the Coulomb scatter differential cross section with solid angle is proportional to 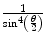 , where θ is the angle through which the projectile is scattered from its original trajectory. The validity conditions for such a classical description are then examined. We then proceed to derivations of this differential cross section through quantum-mechanical means. We first use the first term of the Born expansion to yield an expression for the scattering amplitude and, thus, the differential cross section which is in exact agreement with that derived classically. But as the Coulomb potential does not satisfy the requirements of this approximation, we extend the Born expansion to second order for the Coulomb potential and determine that this second-order term will diverge, but can be made convergent for a screened charged target. An exact nonrelativistic quantum-mechanical solution for the Coulomb scattering differential cross section is then derived from the Schrödinger equation and compared to the classical results and that based upon the Born expansion. The problem of electron (Mott) scattering, in which the intrinsic spin of the electron is not neglected, is examined and a differential cross section derived from Dirac theory. Finally, the case of electron–electron (Møller) scatter and the inherent need to account for spin statistics and the indistinguishability between the electrons in the final state is derived.
, where θ is the angle through which the projectile is scattered from its original trajectory. The validity conditions for such a classical description are then examined. We then proceed to derivations of this differential cross section through quantum-mechanical means. We first use the first term of the Born expansion to yield an expression for the scattering amplitude and, thus, the differential cross section which is in exact agreement with that derived classically. But as the Coulomb potential does not satisfy the requirements of this approximation, we extend the Born expansion to second order for the Coulomb potential and determine that this second-order term will diverge, but can be made convergent for a screened charged target. An exact nonrelativistic quantum-mechanical solution for the Coulomb scattering differential cross section is then derived from the Schrödinger equation and compared to the classical results and that based upon the Born expansion. The problem of electron (Mott) scattering, in which the intrinsic spin of the electron is not neglected, is examined and a differential cross section derived from Dirac theory. Finally, the case of electron–electron (Møller) scatter and the inherent need to account for spin statistics and the indistinguishability between the electrons in the final state is derived.
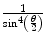 , where θ is the angle through which the projectile is scattered from its original trajectory. The validity conditions for such a classical description are then examined. We then proceed to derivations of this differential cross section through quantum-mechanical means. We first use the first term of the Born expansion to yield an expression for the scattering amplitude and, thus, the differential cross section which is in exact agreement with that derived classically. But as the Coulomb potential does not satisfy the requirements of this approximation, we extend the Born expansion to second order for the Coulomb potential and determine that this second-order term will diverge, but can be made convergent for a screened charged target. An exact nonrelativistic quantum-mechanical solution for the Coulomb scattering differential cross section is then derived from the Schrödinger equation and compared to the classical results and that based upon the Born expansion. The problem of electron (Mott) scattering, in which the intrinsic spin of the electron is not neglected, is examined and a differential cross section derived from Dirac theory. Finally, the case of electron–electron (Møller) scatter and the inherent need to account for spin statistics and the indistinguishability between the electrons in the final state is derived.
, where θ is the angle through which the projectile is scattered from its original trajectory. The validity conditions for such a classical description are then examined. We then proceed to derivations of this differential cross section through quantum-mechanical means. We first use the first term of the Born expansion to yield an expression for the scattering amplitude and, thus, the differential cross section which is in exact agreement with that derived classically. But as the Coulomb potential does not satisfy the requirements of this approximation, we extend the Born expansion to second order for the Coulomb potential and determine that this second-order term will diverge, but can be made convergent for a screened charged target. An exact nonrelativistic quantum-mechanical solution for the Coulomb scattering differential cross section is then derived from the Schrödinger equation and compared to the classical results and that based upon the Born expansion. The problem of electron (Mott) scattering, in which the intrinsic spin of the electron is not neglected, is examined and a differential cross section derived from Dirac theory. Finally, the case of electron–electron (Møller) scatter and the inherent need to account for spin statistics and the indistinguishability between the electrons in the final state is derived.4.1 Introduction
In this chapter, we explore the Coulomb scatter of a moving projectile of charge ze from a bare point target of charge Ze. Depending upon the masses of the projectile and target (or if the target is moving relative to the projectile), the calculation is performed in either the laboratory or centre-of-mass reference systems using the actual or reduced masses, accordingly. This chapter will deal exclusively with elastic scatter as it is concerned with a point projectile undergoing Coulomb scatter with a point target which is not screened. No degrees of freedom which can channel away kinetic energy are considered to be present.
Collisions with an atom will be differentiated between those with an atom as a whole (which Bohr (1948) termed, perhaps rather confusingly, as ‘nuclear’ collisions) and with those with individual atomic electrons (known as ‘electronic’ collisions). In later discussion, we will categorise collisions as ‘soft’ and as ‘hard’, with the differentiation between these being defined by the theoretical model (spatial distance from the atom or energy transfer). The former is, to a reasonable approximation, considered elastic in that the atomic recoils as a whole with a complete transfer of kinetic energy and momentum. The latter is frequently inelastic in that additional energy channels exist which remove kinetic energy and momentum from the projectile. These channels include atomic excitations and, should the energy transfer to the atomic electron exceed its binding energy, ionisation and the ejection of the electron.1 These collisions are primarily responsible for the stopping of a charged particle in a medium.
As the Coulomb interaction is the foundation of the rest of the discussions to follow, it is the focus of this and the following two chapters. We begin by considering the description of Coulomb scatter using classical mechanics. The goal is to calculate the differential cross section in solid angle of the charged projectile being scattered from its trajectory by an angle θ. We will consider two separate ways of evaluating this cross section through classical methods. The first is based upon the scattering integral which relates the scattering angle to both the kinematics of the scatter and the spatial separation between the projectile and target. We will consider this solution in both nonrelativistic and relativistic cases. The use of classical perturbation theory as a means of evaluating the scattering integral concludes the discussion of the scattering integral. The second classical mechanical method investigated of evaluating the Coulomb cross section is based upon the Laplace–Runge–Lenz vector which not only reproduces the differential cross section calculated using the scattering integral but also describes the shape of the trajectory followed by the scattered projectile. We then conclude this section with a detailed examination of the conditions under which descriptions of Coulomb scatter using classical mechanics are valid and the uncertainties that can arise.
Quantum-mechanical descriptions of Coulomb scatter will then follow with the nonrelativistic case considered first. The Born expansion of Chap. 2 is applied to the unscreened Coulomb potential and investigated in detail. The first term of the expansion for Coulomb scatter is evaluated and the differential cross section calculated – a result shown to be the same as that derived from the classical mechanical calculations. However, as a result of the perturbation theory which is the foundation of the Born expansion as an iterative solution to the Lippmann–Schwinger equation, the expansion is strictly valid only for a short-range potential that is weaker than the projectile’s kinetic energy. Because the range of the Coulomb potential is infinite, we will extend the Born expansion to second order in order to more fully investigate its utility in describing the Coulomb interaction.
Going beyond the use of perturbation theory in calculating for Coulomb scatter, the exact solution is derived from the Schrödinger equation. The chapter then concludes with discussion of relativistic Coulomb scatter.
4.2 Classical Mechanical Solutions
4.2.1 Scattering Integral
4.2.1.1 Nonrelativistic Solution
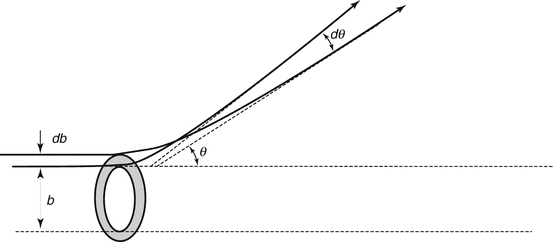
Figure 4.1 describes the basic scattering geometry that we will consider in this discussion.
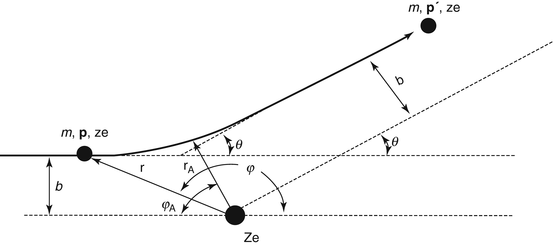

Fig. 4.1
Scattering geometry from an unscreened charged point target of infinite mass (See text for description)
In this figure, a particle of mass m, 3-vector momentum p (and kinetic energy 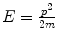 ) and electric charge ze is incident from the left at an impact parameter b from the infinitely massive scattering centre of charge Ze , which is at the origin, and is scattered through the angle θ with a momentum
) and electric charge ze is incident from the left at an impact parameter b from the infinitely massive scattering centre of charge Ze , which is at the origin, and is scattered through the angle θ with a momentum 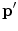 . Note that
. Note that 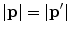 . In this calculation, the target is assumed implicitly to have infinite mass, but should it not, the calculation can be performed in the centre-of-mass reference system and the mass taken to be the reduced mass (see Appendix D). The potential affecting the projectile is the Coulomb,
. In this calculation, the target is assumed implicitly to have infinite mass, but should it not, the calculation can be performed in the centre-of-mass reference system and the mass taken to be the reduced mass (see Appendix D). The potential affecting the projectile is the Coulomb, 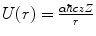 . As the differential cross section for the scatter is the annular area afforded by a differential element of the impact parameter, as shown in Fig. 4.2, we wish to determine the relationship between the scattering angle and the impact parameter. This differential cross section is
. As the differential cross section for the scatter is the annular area afforded by a differential element of the impact parameter, as shown in Fig. 4.2, we wish to determine the relationship between the scattering angle and the impact parameter. This differential cross section is
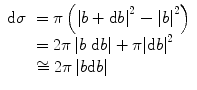
as we will neglect terms in the differential of second order or higher.
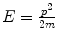 ) and electric charge ze is incident from the left at an impact parameter b from the infinitely massive scattering centre of charge Ze , which is at the origin, and is scattered through the angle θ with a momentum
) and electric charge ze is incident from the left at an impact parameter b from the infinitely massive scattering centre of charge Ze , which is at the origin, and is scattered through the angle θ with a momentum 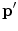 . Note that
. Note that 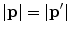 . In this calculation, the target is assumed implicitly to have infinite mass, but should it not, the calculation can be performed in the centre-of-mass reference system and the mass taken to be the reduced mass (see Appendix D). The potential affecting the projectile is the Coulomb,
. In this calculation, the target is assumed implicitly to have infinite mass, but should it not, the calculation can be performed in the centre-of-mass reference system and the mass taken to be the reduced mass (see Appendix D). The potential affecting the projectile is the Coulomb, 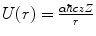 . As the differential cross section for the scatter is the annular area afforded by a differential element of the impact parameter, as shown in Fig. 4.2, we wish to determine the relationship between the scattering angle and the impact parameter. This differential cross section is
. As the differential cross section for the scatter is the annular area afforded by a differential element of the impact parameter, as shown in Fig. 4.2, we wish to determine the relationship between the scattering angle and the impact parameter. This differential cross section is
Fig. 4.2
Scattering geometry for calculating the differential cross section. Azimuthal symmetry exists in Coulomb scattering, and the differential solid angle is dΩ = 2π sinθ dθ
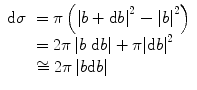
(4.1)
Recall from our discussions of Chap. 2 that we are only able to observe the asymptotic forms of the projectile pre- and post-scatter or, equivalently, at infinite times in the past and in the future. Hence, the angle φ will have the properties
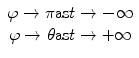
as is immediately evident from Fig. 4.1. The vector r is the radial vector from the scattering centre to the projectile, and the vector r A is the value of r at the point of closest approach (i.e. the periapsis) between the projectile and the scattering centre. Of course, the magnitudes of the radial vector and the polar angle are both functions of time.
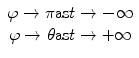
(4.2)
Let us consider conserved mechanical quantities of the scatter. The first will be that of energy. At infinite time in the past (and at infinite distance where there is no influence from the potential), the total energy is kinetic only and given by 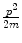 . The conservation of energy is, in cylindrical co-ordinates,
. The conservation of energy is, in cylindrical co-ordinates,
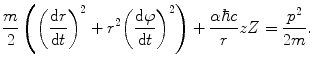
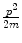 . The conservation of energy is, in cylindrical co-ordinates,
. The conservation of energy is, in cylindrical co-ordinates,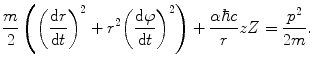
(4.3)
The second conserved mechanical quantity considered is that of angular momentum, the magnitude of which is
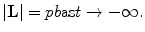
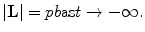
(4.4)
Also from Fig. 4.1, we see that the relationship between the angle φ A and the scattering angle θ is
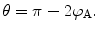
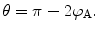
(4.6)
The angle φ A is given by the integral
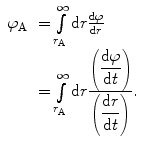
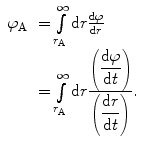
(4.7)
The goal of the calculation reduces now to determining the scattering angle, θ, as a function of the impact parameter b. (4.1) showed the relationship between the physically measurable cross section and this impact parameter. We begin by, as suggested by (4.7), determining the rate of change in φ with r. This requires that the derivatives in the numerator and denominator of the integrand be solved for. That of the numerator is determined by extracting the time dependence of the angle φ from (4.5):
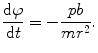
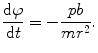
(4.8)
The denominator is calculated by substituting this result into (4.3) to yield the change in the magnitude of the radial vector with time:
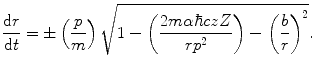
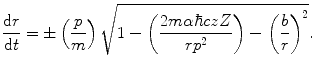
(4.9)
Substituting the two time dependencies of (4.8) and (4.9) into the integral of (4.7) gives the expression for the angle:
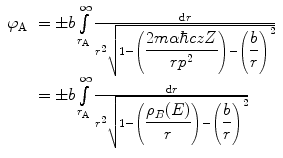
where the spatial parameter
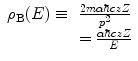
has been defined. This parameter will feature throughout much of our derivations and will be recognised as being the closest distance of approach between the projectile and target if a repulsive Coulomb force exists between the two entities. More subtly, Bohr (1948) termed ρ B(E) as the ‘collision diameter’ for a reason that is to be established following our derivation of the Coulomb scatter differential cross section. An expression for r A can now be obtained by noting that the derivative 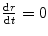 when
when 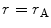 . This is equivalent to the denominator of (4.10) being equal to zero for r = r A or
. This is equivalent to the denominator of (4.10) being equal to zero for r = r A or
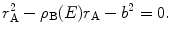
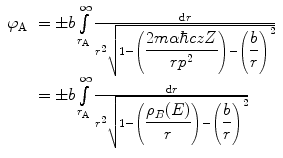
(4.10)
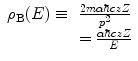
(4.11)
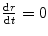 when
when 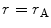 . This is equivalent to the denominator of (4.10) being equal to zero for r = r A or
. This is equivalent to the denominator of (4.10) being equal to zero for r = r A or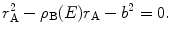
(4.12)
Solving for r A and allowing for only the physically valid solution, we have
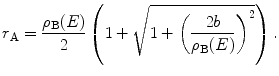
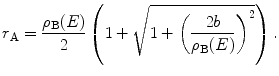
(4.13)
As a result of the conservation of angular momentum, it can be seen that the vector r A defines the axis of symmetry of the projectile’s trajectory. The sign used in (4.10) is positive when the projectile is in the approach phase and negative in the departure phase. Hence, the scattering angle is, from (4.6), given by
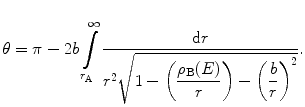
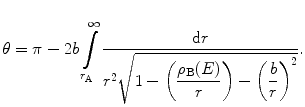
(4.14)
The integral of (4.14), when multiplied by the impact parameter, shall be referred to as the scattering integral. By making the substitution of variable, 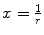 , this expression for the scattering angle becomes
, this expression for the scattering angle becomes
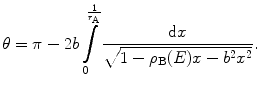
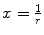 , this expression for the scattering angle becomes
, this expression for the scattering angle becomes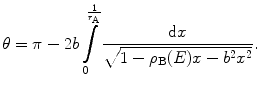
(4.15)
This integral is of the form with the solution
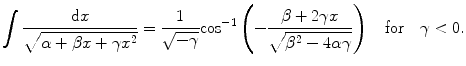
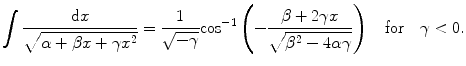
(4.16)
Using this, the solution to the scattering integral is
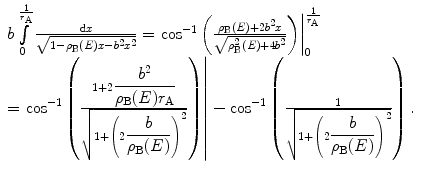

(4.17)
Use of (4.13) followed by tedious algebraic manipulation of the argument of the first cos−1 function (which we shall omit) shows that
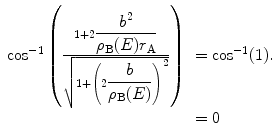
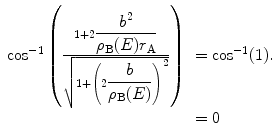
(4.18)
Thus, the scattering angle is given by the expression
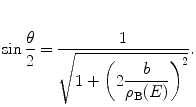
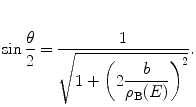
(4.19)
We can then use this result to solve for the impact parameter as a function of scattering angle:
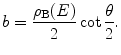
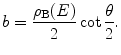
(4.20)
The result of (4.20), which was derived originally via a similar approach taken by Thomson (1906), is the functional link between scattering angle and impact parameter that we sought. More importantly, it leads directly to the physical observable of the differential cross section in solid angle. We can show this by first differentiating (4.20) with respect to scattering angle:
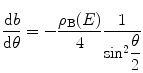
and then substituting this result and (4.20) into the expression for the differential cross section given by (4.1) to arrive at
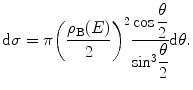
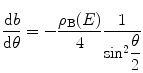
(4.21)
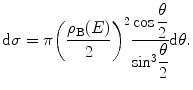
(4.22)
Using
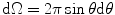 and the trigonometric identity
and the trigonometric identity
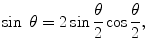 can be rewritten as
can be rewritten as
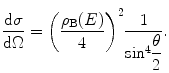
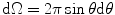
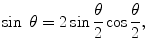
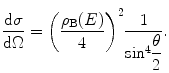
(4.23)
This result is frequently referred to as the Rutherford, or unscreened Coulomb, cross section. We will provide a discussion of the various features of this result which will be of significant later interest in greater detail following the associated derivation using quantum theory.
Why Bohr described the spatial parameter ρ B(E) as the ‘collision diameter’ can now be demonstrated following the above derivation through the use of (4.23). From (4.20), it follows that the condition of backscatter (i.e. that of the scattering angle θ exceeding π/2) corresponds to the inequality of ρ B(E) ≥ 2b. That is,
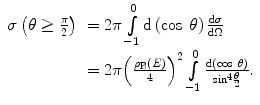
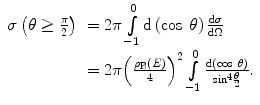
(4.24)
The integral is solved using the trigonometric identity, 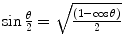 , and the substitution of variable
, and the substitution of variable 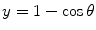 to give the result
to give the result
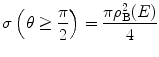
which is equal to the area of a circle of diameter ρ B and, hence, leading to Bohr’s description of it as the collision diameter. Although ρ B is a classically derived quantity, its functional form will appear throughout our discussions due to its convenience.
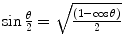 , and the substitution of variable
, and the substitution of variable 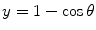 to give the result
to give the result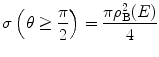
(4.25)
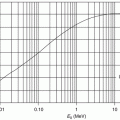
Figure 4.3 shows the dependence of the Bohr scattering diameter, normalised to the zZ product of the projectile and target charges, as a function of the projectile’s kinetic energy. This shows the reciprocal dependence of the Bohr scattering diameter with kinetic energy for a fixed zZ product and implies the decrease for fixed kinetic energy and increasing Coulomb potential. This also leads to the consideration of the conditions of validity over which the classical Coulomb scattering calculation is valid, which are to be discussed in Sect. 4.2.3.
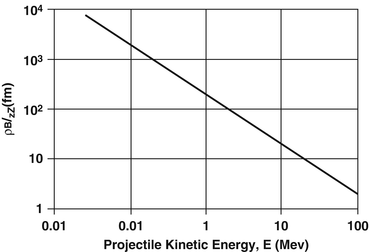

Fig. 4.3
The Bohr scattering diameter normalised to the product of the projectile and charge zZ values as a function of projectile energy
4.2.1.2 Relativistic Solution
The extension of the above derivation to relativistic energies begins through the expression of the conservation of energy in the form given by
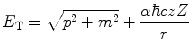
where E T is the total energy of the projectile (rather than only the kinetic energy we have considered previously). Using the conservation of angular momentum in cylindrical co-ordinates, we have
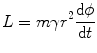
where 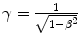 and
and 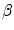 is the velocity normalised to the speed of light. Thus, we have
is the velocity normalised to the speed of light. Thus, we have
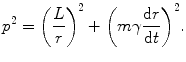
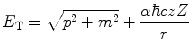
(4.26)
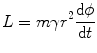
(4.27)
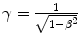 and
and 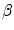 is the velocity normalised to the speed of light. Thus, we have
is the velocity normalised to the speed of light. Thus, we have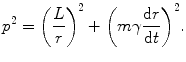
(4.28)
By calculating p 2 from (4.26) and equating this with (4.28), we achieve the derivative of the radial distance with respect to time:
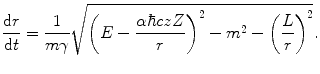
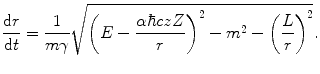
(4.29)
We follow our earlier procedure of the substitution of variable 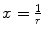 to arrive at
to arrive at
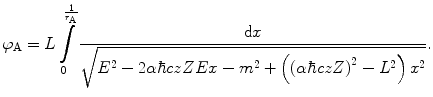
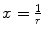 to arrive at
to arrive at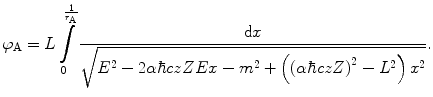
(4.32)
Recalling that 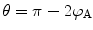 and using a result from the tables of Abramowitz and Stegun (1972), the scattering angle is
and using a result from the tables of Abramowitz and Stegun (1972), the scattering angle is
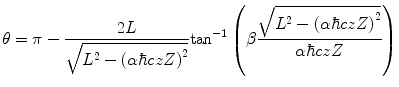
where β is the projectile velocity normalised to that of light. Clearly, this classical result of (4.33) can be valid only for large values of angular momentum, i.e. 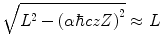 and (4.33) will simplify to the expression
and (4.33) will simplify to the expression
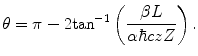
 and using a result from the tables of Abramowitz and Stegun (1972), the scattering angle is
and using a result from the tables of Abramowitz and Stegun (1972), the scattering angle is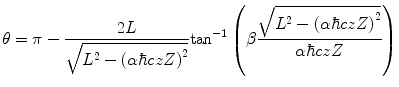
(4.33)
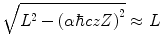 and (4.33) will simplify to the expression
and (4.33) will simplify to the expression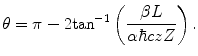
(4.34)
Further simplification can be achieved by writing the angular momentum as the product of projectile momentum and impact parameter 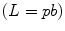 , allowing us to write an expression for the scattering angle in the simpler form
, allowing us to write an expression for the scattering angle in the simpler form

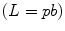 , allowing us to write an expression for the scattering angle in the simpler form
, allowing us to write an expression for the scattering angle in the simpler form
(4.35)
4.2.1.3 Classical Perturbation Theory
In Chap. 2, we developed quantum perturbation theory from first principles and, in particular, derived the Born expansion in terms of the summation of powers of the perturbing potential subject to the ‘weakness’ of the perturbing potential relative to the projectile’s kinetic energy. While these quantum results will be examined later in this chapter for the specific case of the Coulomb potential, we investigate the use of classical perturbation theory in calculating the scattering integral. Classical perturbation theory will also play a role in our later discussion of energy transfer during a collision.
In order to advance the general nature of the method, we will not impose the requirement that the potential U(r) be Coulombic. The form of the scattering integral is, in this general case,
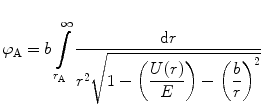
where, as we are considering nonrelativistic kinematics,  is the kinetic energy of the projectile. If an analytical solution of (4.36) does not exist or else is too laborious to derive, the integral may be solved numerically in order to yield the angle
is the kinetic energy of the projectile. If an analytical solution of (4.36) does not exist or else is too laborious to derive, the integral may be solved numerically in order to yield the angle 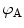 . As a result, one may question what utility of the iterative approach is provided by perturbation theory in solving this equation. Depending upon the nature of the potential, the first-order term of the perturbative expansion may be useful and easier to use than either a numerical solution to the integral or the inclusion of further terms obtained by iteration. Hence, examination of a higher-order term may indicate that the lower-order term expansion is sufficient and practical.
. As a result, one may question what utility of the iterative approach is provided by perturbation theory in solving this equation. Depending upon the nature of the potential, the first-order term of the perturbative expansion may be useful and easier to use than either a numerical solution to the integral or the inclusion of further terms obtained by iteration. Hence, examination of a higher-order term may indicate that the lower-order term expansion is sufficient and practical.
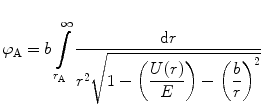
(4.36)
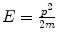 is the kinetic energy of the projectile. If an analytical solution of (4.36) does not exist or else is too laborious to derive, the integral may be solved numerically in order to yield the angle
is the kinetic energy of the projectile. If an analytical solution of (4.36) does not exist or else is too laborious to derive, the integral may be solved numerically in order to yield the angle 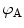 . As a result, one may question what utility of the iterative approach is provided by perturbation theory in solving this equation. Depending upon the nature of the potential, the first-order term of the perturbative expansion may be useful and easier to use than either a numerical solution to the integral or the inclusion of further terms obtained by iteration. Hence, examination of a higher-order term may indicate that the lower-order term expansion is sufficient and practical.
. As a result, one may question what utility of the iterative approach is provided by perturbation theory in solving this equation. Depending upon the nature of the potential, the first-order term of the perturbative expansion may be useful and easier to use than either a numerical solution to the integral or the inclusion of further terms obtained by iteration. Hence, examination of a higher-order term may indicate that the lower-order term expansion is sufficient and practical.In our use of classical perturbation theory in evaluating the scattering integral, we will follow the approaches previously described by Lehmann and Leibfried (1963), Andersen and Sigmund (1966) and Sigmund and Schinner (2000). Why the use of perturbation theory should be preferable to a straightforward Taylor’s expansion is made immediately apparent upon expansion of the square root in the denominator of the integrand of (4.36) in terms of the potential:
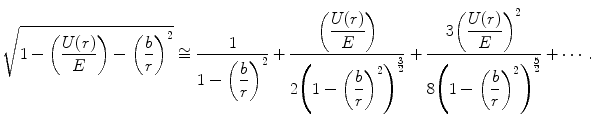
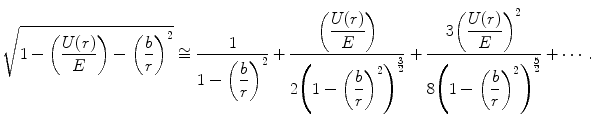
(4.37)
We see immediately the singularities that occur when r = b.
The perturbation solution to the scattering integral of (4.36) is achieved by using contour integration in the complex r-plane as shown in Fig. 4.4.2
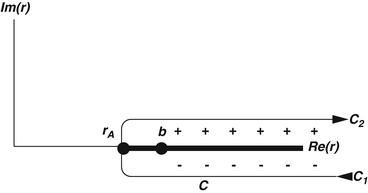

Fig. 4.4
Integration contour in the complex r-plane to be used to solve (4.36) using perturbation theory
The integrand of (4.36) is multi-valued in the complex r-plane. However, it is possible to make it single valued if a cut is made along the real axis for r > r A, as shown in Fig. 4.4. Thus, the positive value is approached from the +Im(r) plane, whereas the negative value is approached from the −Im(r) plane. We then write the scattering integral over this contour around the branch cut as
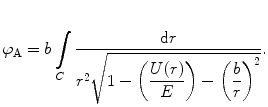
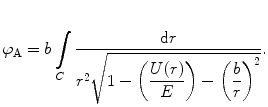
(4.38)
The contour bypasses the cut which, as the integrand is regular3 external to the cut, makes use of the Cauchy–Goursat theorem. Thus,
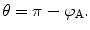
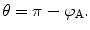
(4.39)
We now apply the Taylor expansion, in this example, to the first three terms in U(r):
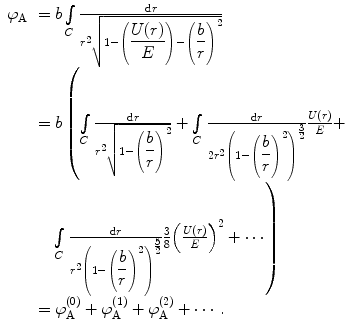
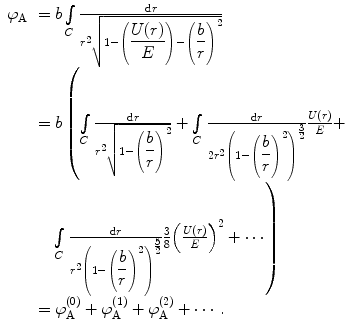
(4.40)
In this example, we evaluate each of these three terms in turn. The first (zeroth-order) term is
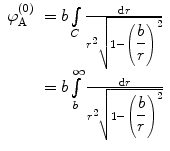
where the path of integration has been manipulated towards the real axis. In this case, the zeroth-order approximation to the scattering angle is 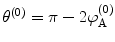 . By using the exchange of variable
. By using the exchange of variable 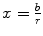 , the zeroth-order term of the expansion of the scattering integral is
, the zeroth-order term of the expansion of the scattering integral is
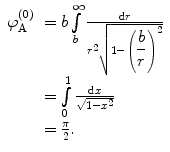
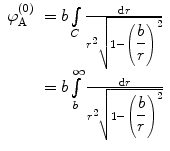
(4.41)
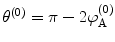 . By using the exchange of variable
. By using the exchange of variable 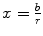 , the zeroth-order term of the expansion of the scattering integral is
, the zeroth-order term of the expansion of the scattering integral is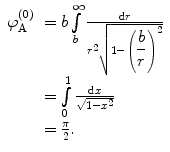
(4.42)
Thus, the scattering angle corresponding to this term is
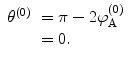
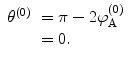
That this result of a zero scattering angle should be the case is intuitive: the perturbing potential does not appear in the zeroth-order term of the integrand of (4.41); hence, there can be no interaction between projectile and target, and the scattering angle must be zero.
The second term of the scattering integral expansion is
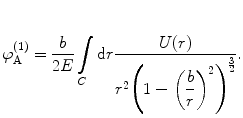
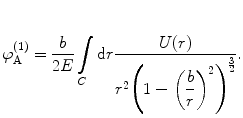
(4.43)
This integral can be solved by parts by first noting the derivative:
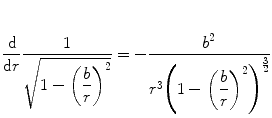 which enables us to write (4.43) in the form
which enables us to write (4.43) in the form
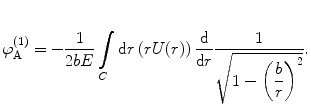
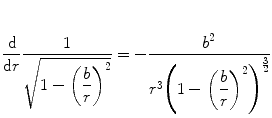
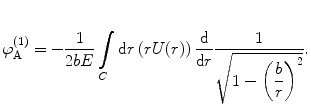
(4.44)
Partial integration is then used to yield
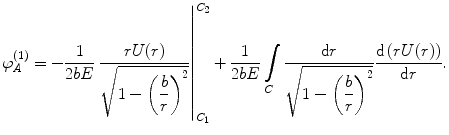
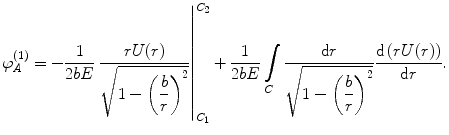
(4.45)
This result can be left as is for any arbitrary scattering potential. However, to continue further this examination for a Coulomb-like potential, we treat U(r) as a Yukawa or Wentzel potential modelling a screened charged source with the screening parameter, κ, 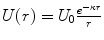 . The integrated term of (4.45) is, then,
. The integrated term of (4.45) is, then,
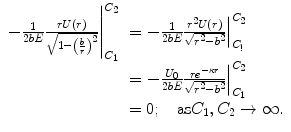
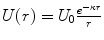 . The integrated term of (4.45) is, then,
. The integrated term of (4.45) is, then,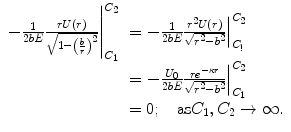
(4.46)
We solve for this by using the exchange of variables within the integral, 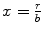




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree