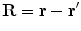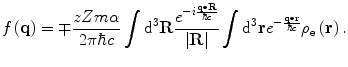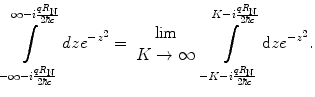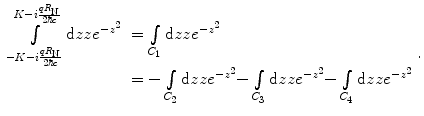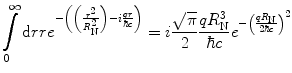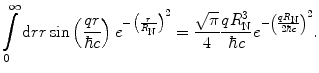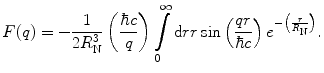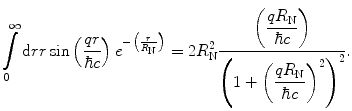(1)
Amersham, Buckinghamshire, UK
5.1 Introduction
5.2.1 Form Factor: Definition
5.3 Screened Charges
5.3.1 Introduction
5.3.3 Screening Conditions
5.4.1 Introduction
5.4.2 Nuclear Form Factor
5.5.1 Qualitative Differences
Abstract
With the exception of point targets, such as a free electron, the target in the elastic Coulomb scatter of a charged particle is typically distributed and screened, such as the atomic nucleus. The degree of spatial variation and Coulomb screening perceived by the projectile will be dependent upon its de Broglie wavelength of both the atom and the nucleus. In this chapter, we extend the previous discussion of elastic Coulomb scatter from a point charge to the more realistic case of a distributed and screened target. This will begin with the definition of the form factor for a spatially distributed charge that the projectile is incident to. Examples such as a hard-edge homogeneous sphere and a sphere with a charge distribution with a Gaussian radial charge distribution are considered in the calculation of these form factors.
Screened target are next considered and in much detail. We begin with the simple model of continuous screening using a Yukawa-type potential to represent that of the screened nuclear potential. A key parameter used in this model is the atomic electron screening parameter, which is the coefficient of the spatial variable in the exponent of the Yukawa form. The Thomas–Fermi statistical model of the atom is developed and its results used to derive a functional form of the atomic electron screening parameter.
We then proceed to the model of discrete screening in which the potential perceived by the projectile is the summation of those due to the atomic electrons and that due to the atomic nucleus. From this calculation is extracted the atomic elastic scattering form factor.
The outcomes of the continuous and discrete atomic electron screening models are differential cross sections which display modifications from the Rutherford (unscreened) Coulomb differential cross section which avoid the divergence at zero scattering angle.
We conclude with a numerical analysis of these results.
5.1 Introduction
In the previous chapter, the elastic Coulomb scatter differential cross sections for a point charged projectile incident to a point bare charged target (i.e. Rutherford scatter) were evaluated as functions of momentum transfer and solid angle in both classical and quantum-mechanical models. The result in solid angle has a 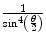 dependence which leads to the divergence
dependence which leads to the divergence 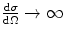 as
as 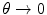 .
.
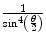 dependence which leads to the divergence
dependence which leads to the divergence 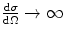 as
as 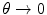 .
.In practice, the target is not a bare point. It is the nucleus which, in the Coulomb picture, is a spatial distribution of protons and, hence, cannot be considered a point if the projectile’s de Broglie wavelength is sufficiently small. Further, the nucleus resides within a cloud of atomic electrons bound to the nucleus. The nuclear Coulomb field experienced by the projectile will thus vary with projectile–nucleus separation in a manner different from the inverse square law due to the shielding of the nuclear charge by these electrons.
In this chapter, we will investigate these effects upon the elastic Coulomb differential cross section. Atomic electron screening will, in particular, remove the divergence noted above and the differential cross section will reach a finite value as 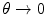 . On the other hand, the tendency of the finite nuclear spatial distribution will be to diminish the cross section at larger angles or, in some cases, introduce a diffraction-like behaviour with angle. The combination of both cases leads to elastic Coulomb scatter being predominantly forward directed and to the phenomenon of multiple scatter (which is the subject of the following chapter).
. On the other hand, the tendency of the finite nuclear spatial distribution will be to diminish the cross section at larger angles or, in some cases, introduce a diffraction-like behaviour with angle. The combination of both cases leads to elastic Coulomb scatter being predominantly forward directed and to the phenomenon of multiple scatter (which is the subject of the following chapter).
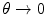 . On the other hand, the tendency of the finite nuclear spatial distribution will be to diminish the cross section at larger angles or, in some cases, introduce a diffraction-like behaviour with angle. The combination of both cases leads to elastic Coulomb scatter being predominantly forward directed and to the phenomenon of multiple scatter (which is the subject of the following chapter).
. On the other hand, the tendency of the finite nuclear spatial distribution will be to diminish the cross section at larger angles or, in some cases, introduce a diffraction-like behaviour with angle. The combination of both cases leads to elastic Coulomb scatter being predominantly forward directed and to the phenomenon of multiple scatter (which is the subject of the following chapter).We begin this chapter by considering the nuclear target as a spatial distribution 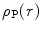 of protons. The result of this analysis will be that the (unscreened) Rutherford cross section is modified by the modulus squared of the nuclear form factor, which will be shown to be equal to the Fourier transform of
of protons. The result of this analysis will be that the (unscreened) Rutherford cross section is modified by the modulus squared of the nuclear form factor, which will be shown to be equal to the Fourier transform of 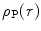 . 1 Examples of this quantity are derived for a variety of simple spherically symmetric charge distributions. We must also recognise, however, that with positrons and electrons (i.e. charged leptons), the effect of the finite nuclear size is purely electromagnetic in character through their interactions with the nuclear protons. On the other hand, for hadrons (protons, π−-mesons, α-particles and ions) that are used as medical radiations, there is the additional contribution of the attractive strong nuclear force. As the range of this force is of only the order of 1–2 fm, its effect would not be evident in most interactions of medical radiation interest unless there were sufficient overlap between the hadron projectile and nuclear wavefunctions, such as in the formation of a pionic atom and the resulting production of star products as described in Chap. 1. We will, however, limit the discussion of this chapter to electromagnetic interactions.
. 1 Examples of this quantity are derived for a variety of simple spherically symmetric charge distributions. We must also recognise, however, that with positrons and electrons (i.e. charged leptons), the effect of the finite nuclear size is purely electromagnetic in character through their interactions with the nuclear protons. On the other hand, for hadrons (protons, π−-mesons, α-particles and ions) that are used as medical radiations, there is the additional contribution of the attractive strong nuclear force. As the range of this force is of only the order of 1–2 fm, its effect would not be evident in most interactions of medical radiation interest unless there were sufficient overlap between the hadron projectile and nuclear wavefunctions, such as in the formation of a pionic atom and the resulting production of star products as described in Chap. 1. We will, however, limit the discussion of this chapter to electromagnetic interactions.
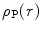 of protons. The result of this analysis will be that the (unscreened) Rutherford cross section is modified by the modulus squared of the nuclear form factor, which will be shown to be equal to the Fourier transform of
of protons. The result of this analysis will be that the (unscreened) Rutherford cross section is modified by the modulus squared of the nuclear form factor, which will be shown to be equal to the Fourier transform of 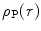 . 1 Examples of this quantity are derived for a variety of simple spherically symmetric charge distributions. We must also recognise, however, that with positrons and electrons (i.e. charged leptons), the effect of the finite nuclear size is purely electromagnetic in character through their interactions with the nuclear protons. On the other hand, for hadrons (protons, π−-mesons, α-particles and ions) that are used as medical radiations, there is the additional contribution of the attractive strong nuclear force. As the range of this force is of only the order of 1–2 fm, its effect would not be evident in most interactions of medical radiation interest unless there were sufficient overlap between the hadron projectile and nuclear wavefunctions, such as in the formation of a pionic atom and the resulting production of star products as described in Chap. 1. We will, however, limit the discussion of this chapter to electromagnetic interactions.
. 1 Examples of this quantity are derived for a variety of simple spherically symmetric charge distributions. We must also recognise, however, that with positrons and electrons (i.e. charged leptons), the effect of the finite nuclear size is purely electromagnetic in character through their interactions with the nuclear protons. On the other hand, for hadrons (protons, π−-mesons, α-particles and ions) that are used as medical radiations, there is the additional contribution of the attractive strong nuclear force. As the range of this force is of only the order of 1–2 fm, its effect would not be evident in most interactions of medical radiation interest unless there were sufficient overlap between the hadron projectile and nuclear wavefunctions, such as in the formation of a pionic atom and the resulting production of star products as described in Chap. 1. We will, however, limit the discussion of this chapter to electromagnetic interactions.Following our derivation of the modification of the Rutherford cross section by a finite nuclear size, we then proceed to an investigation of the screened atomic target and develop it in two ways. We note that this requires our determination of the spatial distribution of the atomic electrons, 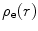 .
.
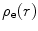 .
.In the first, the screening is considered to result in a continuous and exponentially decreasing Coulomb potential with decreasing distance r from the nucleus (i.e. a Wentzel type of potential, i.e. 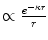 , where
, where 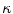 is the screening parameter). The scattering differential cross section for this screened potential is calculated from the first-order term of the Born series for this screened potential. Following an exposition given by Bohr (1948), we then proceed to analyse the various conditions of scattering arising from the exponentially screened Coulomb potential and the underlying roles of kinematics and the dimensions of the electron cloud surrounding the nucleus.2
is the screening parameter). The scattering differential cross section for this screened potential is calculated from the first-order term of the Born series for this screened potential. Following an exposition given by Bohr (1948), we then proceed to analyse the various conditions of scattering arising from the exponentially screened Coulomb potential and the underlying roles of kinematics and the dimensions of the electron cloud surrounding the nucleus.2
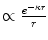 , where
, where 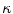 is the screening parameter). The scattering differential cross section for this screened potential is calculated from the first-order term of the Born series for this screened potential. Following an exposition given by Bohr (1948), we then proceed to analyse the various conditions of scattering arising from the exponentially screened Coulomb potential and the underlying roles of kinematics and the dimensions of the electron cloud surrounding the nucleus.2
is the screening parameter). The scattering differential cross section for this screened potential is calculated from the first-order term of the Born series for this screened potential. Following an exposition given by Bohr (1948), we then proceed to analyse the various conditions of scattering arising from the exponentially screened Coulomb potential and the underlying roles of kinematics and the dimensions of the electron cloud surrounding the nucleus.2 We next consider the means of evaluating numerically the effects of screening. This will be largely based upon the Thomas–Fermi statistical model of multi-electron atoms which is then derived. There are three reasons for our focus on the Thomas–Fermi approach. First, it provides a number of analytical expressions of the atomic electron screening parameter used in the exponentially screened potential and which are readily scaled between particular atoms. Second, the model itself provides an expression of an effective potential that can be used to calculate for the screened Coulomb scatter differential cross section. Third, it will be referred to in later discussions of charged particle energy loss. However, the Thomas–Fermi result is not analytical, and thus its practical implementation requires either a numerical calculation in order for it to be evaluated or else to be approximated by an analytical formula (as given in the multiexponential approximation of Molière).
In the second approach of accounting for screening, the scattering centre is treated explicitly as a nucleus surrounded by a discrete number of noninteracting electrons such that the Coulomb scattering potential felt by the projectile is the sum of the individual contributions of these sources. A differential cross section is calculated from these contributions using quantum perturbation theory and the results compared with the continuous-screening model. The chapter concludes with numerical examples of calculations for carbon and calcium targets, because their presences within tissue and their large differences in atomic number Z will be used as the elemental targets for these calculations.
Throughout, where numerical data are introduced in order to assist the reader in understanding the orders of magnitude of the quantities discussed, we will cite examples of 100-keV electrons and 250-MeV protons incident to carbon and calcium. The particles and kinetic energies are typical of many medical applications of these projectiles, and the target selection covers the range of atomic numbers relevant to tissue.3
5.2 Spatially Distributed Targets
5.2.1 Form Factor: Definition
Instead of the point charge discussed throughout Chap. 4, let us now consider the target to be a spatially distributed electric charge, such as the nucleus, with a charge density function 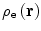 with unit normalisation:
with unit normalisation:
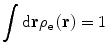
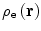 with unit normalisation:
with unit normalisation: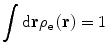
(5.1)
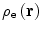 is the number density/spatial distribution of protons within the nucleus normalised to Z. This unit normalisation is selected for this specific discussion as it leads to form factors such that
is the number density/spatial distribution of protons within the nucleus normalised to Z. This unit normalisation is selected for this specific discussion as it leads to form factors such that ![$$ {{\left| {F(q)} \right|}^2}\in \left[ {0,1} \right] $$](/wp-content/uploads/2016/04/A306762_1_En_5_Chapter_IEq000512.gif) . Clearly, we could change the normalisation of (5.1) such that the integral is equal to the atomic number of the target, Z, and such non-unity normalisations are used in general in later discussions within the context of the atomic electron spatial distribution. This normalisation (which gives the dimension of the density function as that of inverse volume) is also used as it allows the Z charge of the target to be explicitly noted in the expression of the distributed Coulomb potential:
. Clearly, we could change the normalisation of (5.1) such that the integral is equal to the atomic number of the target, Z, and such non-unity normalisations are used in general in later discussions within the context of the atomic electron spatial distribution. This normalisation (which gives the dimension of the density function as that of inverse volume) is also used as it allows the Z charge of the target to be explicitly noted in the expression of the distributed Coulomb potential: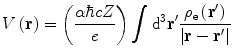
(5.2)
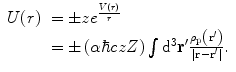
(5.3)
Spherical symmetry will soon be applied (i.e. 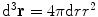 ) so as to simplify the calculation and to reflect the azimuthal independence of Coulomb scatter.
) so as to simplify the calculation and to reflect the azimuthal independence of Coulomb scatter.
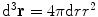 ) so as to simplify the calculation and to reflect the azimuthal independence of Coulomb scatter.
) so as to simplify the calculation and to reflect the azimuthal independence of Coulomb scatter.In order to calculate the differential cross section of the scattering from this distributed charge, we use the scattering amplitude evaluated from the first term of the Born expansion as derived in Chap. 2. This is a function of the three-vector momentum transfer 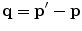 , where
, where 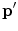 is the post-scatter momentum and p is the incident momentum (for elastic scatter,
is the post-scatter momentum and p is the incident momentum (for elastic scatter, 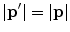 ). The scattering amplitude is
). The scattering amplitude is
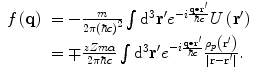
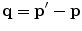 , where
, where 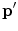 is the post-scatter momentum and p is the incident momentum (for elastic scatter,
is the post-scatter momentum and p is the incident momentum (for elastic scatter, 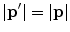 ). The scattering amplitude is
). The scattering amplitude is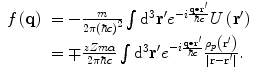
(5.4)
Let us now compare this scattering amplitude for a distributed charge with that derived previously for a point charge (2.83). We see that the latter has now been scaled by the integral, 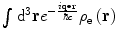 , which is the Fourier transform into q-space of the nuclear proton spatial distribution. Thus, the unscreened point target (Rutherford) differential cross section is modified by the modulus squared of this Fourier transform to yield the differential cross section for a distributed target:
, which is the Fourier transform into q-space of the nuclear proton spatial distribution. Thus, the unscreened point target (Rutherford) differential cross section is modified by the modulus squared of this Fourier transform to yield the differential cross section for a distributed target:
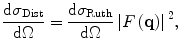
where the form factor is given by the Fourier transform of the electric charge distribution of the target
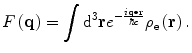
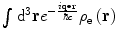 , which is the Fourier transform into q-space of the nuclear proton spatial distribution. Thus, the unscreened point target (Rutherford) differential cross section is modified by the modulus squared of this Fourier transform to yield the differential cross section for a distributed target:
, which is the Fourier transform into q-space of the nuclear proton spatial distribution. Thus, the unscreened point target (Rutherford) differential cross section is modified by the modulus squared of this Fourier transform to yield the differential cross section for a distributed target: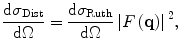
(5.6)
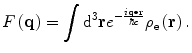
(5.7)
The dependence of the form factor upon the scattering angle arises through the magnitude of the momentum transfer 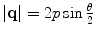 that is within the exponent of the integrand. Clearly, as noted earlier, from the normalisation of the electric charge distribution given by (5.1),
that is within the exponent of the integrand. Clearly, as noted earlier, from the normalisation of the electric charge distribution given by (5.1), ![$$ {{\left| {F\left( \mathbf{q} \right)} \right|}^2}\in\left[ {0,1} \right] $$](/wp-content/uploads/2016/04/A306762_1_En_5_Chapter_IEq000520.gif) . At high momentum transfers, the phase term in (5.5) rapidly oscillates and the integral consequently averages to zero, i.e.
. At high momentum transfers, the phase term in (5.5) rapidly oscillates and the integral consequently averages to zero, i.e. 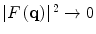 as q → ∞. It is also immediately evident from (5.1) and (5.6) that
as q → ∞. It is also immediately evident from (5.1) and (5.6) that 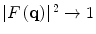 as q → 0.
as q → 0.
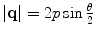 that is within the exponent of the integrand. Clearly, as noted earlier, from the normalisation of the electric charge distribution given by (5.1),
that is within the exponent of the integrand. Clearly, as noted earlier, from the normalisation of the electric charge distribution given by (5.1), ![$$ {{\left| {F\left( \mathbf{q} \right)} \right|}^2}\in\left[ {0,1} \right] $$](/wp-content/uploads/2016/04/A306762_1_En_5_Chapter_IEq000520.gif) . At high momentum transfers, the phase term in (5.5) rapidly oscillates and the integral consequently averages to zero, i.e.
. At high momentum transfers, the phase term in (5.5) rapidly oscillates and the integral consequently averages to zero, i.e. 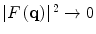 as q → ∞. It is also immediately evident from (5.1) and (5.6) that
as q → ∞. It is also immediately evident from (5.1) and (5.6) that 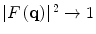 as q → 0.
as q → 0.5.2.2 Form Factors of Specific Charge Spatial Distributions
5.2.2.1 Spherically Symmetric Charge Distributions
Examples of charge distributions that are spherically symmetric will be considered here. The assumption of continuous electric proton charge distribution makes ease of the calculation of the effects of a finite charge distribution, such as the nucleus, upon the scattering cross section. A calculation for a discrete distribution of protons within the nucleus is also possible, but this requires knowledge of the nuclear wavefunction which may not always be known to great precision (Glauber and Matthiae 1970). However, such evaluations are not of practical interest to medical radiation dosimetry calculations.
For a continuous and spherically symmetric charge distribution, the form factor can be simplified to the following integral which can be solved to yield a final expression in terms of the charge spatial distribution:
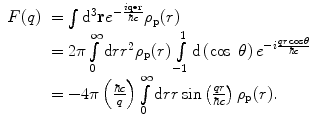
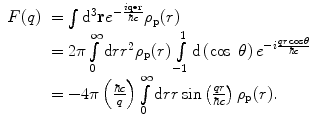
(5.8)
5.2.2.2 Point Charge Distribution
Before progressing, it must be verified first that we can recover the result for a point charge target from (5.8) (which is equivalent to stating that 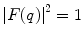 for a point charge). In this case the spatial distribution of the target electric charge is described by the Dirac δ-function:
for a point charge). In this case the spatial distribution of the target electric charge is described by the Dirac δ-function:
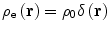
where the normalisation constant is determined from (5.1),
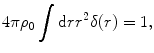
giving 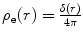 . Substituting this into (5.8) yields the expected constant form factor modulus squared,
. Substituting this into (5.8) yields the expected constant form factor modulus squared, 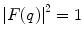 .
.
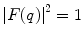 for a point charge). In this case the spatial distribution of the target electric charge is described by the Dirac δ-function:
for a point charge). In this case the spatial distribution of the target electric charge is described by the Dirac δ-function: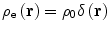
(5.9)
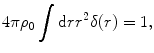
(5.10)
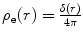 . Substituting this into (5.8) yields the expected constant form factor modulus squared,
. Substituting this into (5.8) yields the expected constant form factor modulus squared, 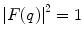 .
.5.2.2.3 Hard-Edge and Homogeneous Spherical Charge Distribution
This is the case of the proton charge distribution uniformly distributed within a spherical nucleus with a well-defined and finite radius R N. This is described by
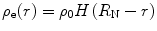
where ρ 0 is a constant and H(x) is the Heaviside function. The parameter R N will be set equal to the root mean square nuclear radius given by the empirical formula 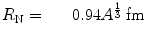 (McParland 2010). This reflects a crude model of the nucleus whereas, in reality, the nuclear edge demonstrates a smooth and continuous decrease in electric charge with radius. ρ 0 is again determined from the normalisation condition of (5.1):
(McParland 2010). This reflects a crude model of the nucleus whereas, in reality, the nuclear edge demonstrates a smooth and continuous decrease in electric charge with radius. ρ 0 is again determined from the normalisation condition of (5.1):
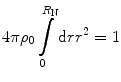
yielding
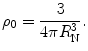
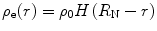
(5.11)
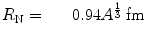 (McParland 2010). This reflects a crude model of the nucleus whereas, in reality, the nuclear edge demonstrates a smooth and continuous decrease in electric charge with radius. ρ 0 is again determined from the normalisation condition of (5.1):
(McParland 2010). This reflects a crude model of the nucleus whereas, in reality, the nuclear edge demonstrates a smooth and continuous decrease in electric charge with radius. ρ 0 is again determined from the normalisation condition of (5.1):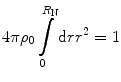
(5.12)
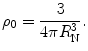
(5.13)
Substituting this into (5.11) and solving for the form factor,
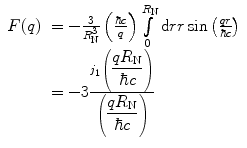
where j 1(x) is the spherical Bessel function of the first kind, as derived in Appendix C. Figure 5.1 shows the hard-edge radial distribution and the modulus squared of the associated form factor.
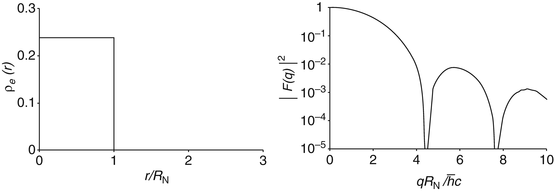
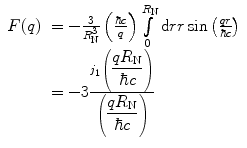
(5.14)

Fig. 5.1
Charge spatial distribution for spherical homogeneous hard-edge target and the corresponding modulus squared of the form factor
This charge distribution yields an oscillatory form factor as a consequence of the diffraction of the incident projectile’s wavefunction by a target with a finite dimension. The dimensionless variable 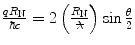 , where
, where  is the reduced de Broglie wavelength, provides the dependence of
is the reduced de Broglie wavelength, provides the dependence of 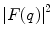 upon the projectile momentum and scattering angle. For
upon the projectile momentum and scattering angle. For 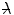 greater than the scattering centre dimensions (i.e. low incident momentum),
greater than the scattering centre dimensions (i.e. low incident momentum), 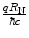 is small and
is small and 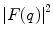 is close to unity such that the modified differential cross section is essentially equal to that of a point target. This reflects the fact that the target is perceived by the projectile as a point for as long as
is close to unity such that the modified differential cross section is essentially equal to that of a point target. This reflects the fact that the target is perceived by the projectile as a point for as long as 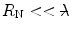 . In general,
. In general, 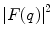 reduces rapidly with decreasing
reduces rapidly with decreasing 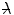 by (ignoring the multiple local minima caused by diffraction) a factor of about 10−3 for
by (ignoring the multiple local minima caused by diffraction) a factor of about 10−3 for 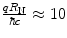 .
.
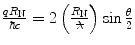 , where
, where 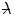 is the reduced de Broglie wavelength, provides the dependence of
is the reduced de Broglie wavelength, provides the dependence of 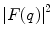 upon the projectile momentum and scattering angle. For
upon the projectile momentum and scattering angle. For 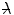 greater than the scattering centre dimensions (i.e. low incident momentum),
greater than the scattering centre dimensions (i.e. low incident momentum), 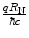 is small and
is small and 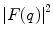 is close to unity such that the modified differential cross section is essentially equal to that of a point target. This reflects the fact that the target is perceived by the projectile as a point for as long as
is close to unity such that the modified differential cross section is essentially equal to that of a point target. This reflects the fact that the target is perceived by the projectile as a point for as long as 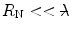 . In general,
. In general, 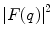 reduces rapidly with decreasing
reduces rapidly with decreasing 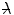 by (ignoring the multiple local minima caused by diffraction) a factor of about 10−3 for
by (ignoring the multiple local minima caused by diffraction) a factor of about 10−3 for 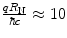 .
.5.2.2.4 Gaussian Charge Distribution
The modelling of the nuclear charge distribution as having a finite radius previously discussed is a rather simplistic and harsh one. Evidence derived from scattering measurements has demonstrated that the nuclear radial charge distribution is smooth, that the nuclear ‘edge’ is diffuse and that, consequently, 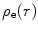 is a continuous function. Here, we consider the use of a Gaussian distribution to describe this radial variation of the charge distribution:
is a continuous function. Here, we consider the use of a Gaussian distribution to describe this radial variation of the charge distribution:
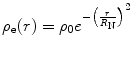
where R N is the radial distance at which the charge distribution is equal to e −1 that of the central value. Experimental evidence indicates that (5.15) is a reasonable model for light nuclei. The example provided in the introduction of the Cauchy–Goursat theorem in Appendix A.3 is useful here. As before, we evaluate  from the normalisation condition of (5.1):
from the normalisation condition of (5.1):
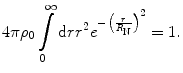
 is a continuous function. Here, we consider the use of a Gaussian distribution to describe this radial variation of the charge distribution:
is a continuous function. Here, we consider the use of a Gaussian distribution to describe this radial variation of the charge distribution: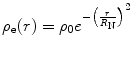
(5.15)
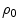 from the normalisation condition of (5.1):
from the normalisation condition of (5.1):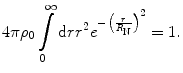
(5.16)
This integral is solved by noting that
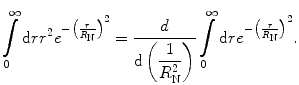
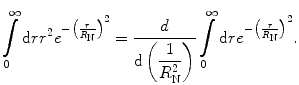
(5.17)
The integral on the right-hand side of (5.17) is solved by first squaring it and creating the double integral:
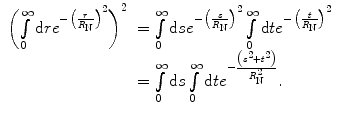
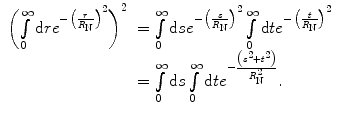
(5.18)
This double integral is solved, in turn, by converting it from Cartesian co-ordinates into polar co-ordinates:
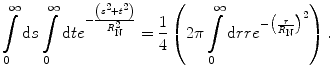
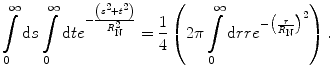
(5.19)
As 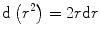 ,
,
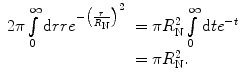
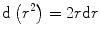 ,
,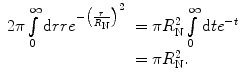
(5.20)
This gives
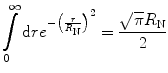
and, hence, from (5.16),
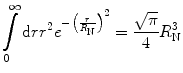
which leads to the normalised Gaussian charge distribution:
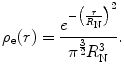
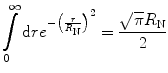
(5.21)
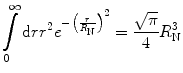
(5.22)
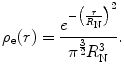
(5.23)
Having obtained this normalised charge distribution, we now evaluate the corresponding form factor
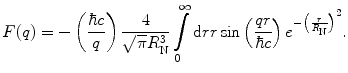
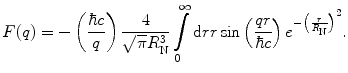
(5.24)
This integral is solved using the complex integration techniques presented in Appendix A. We begin by noting that the integrand is an even function and can thus write the integral as
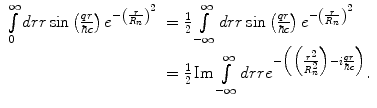
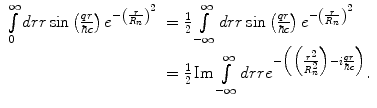
(5.25)
Symmetrising this integral will be shown shortly to be necessary in order to simplify the contour integration that is to follow. The exponent of (5.25) is rewritten as the square
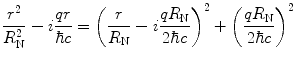
and using the substitution of variable 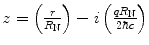 , the integral of (5.25) can be separated into the sum of two simpler integrals:
, the integral of (5.25) can be separated into the sum of two simpler integrals:
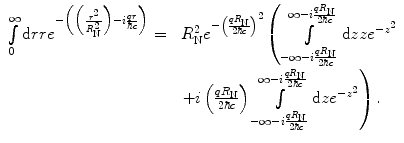
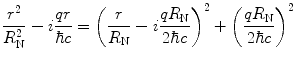
(5.26)
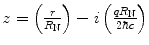 , the integral of (5.25) can be separated into the sum of two simpler integrals:
, the integral of (5.25) can be separated into the sum of two simpler integrals: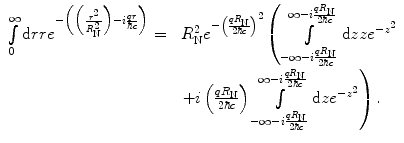
(5.27)
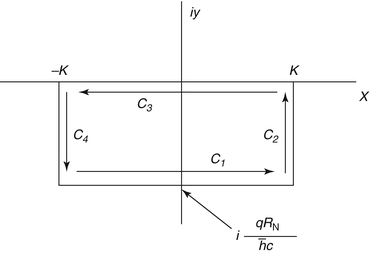
Both integrals are solved by using the Cauchy–Goursat integral theorem, given in Appendix A.3, and which states that the contour integral 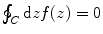 , provided that the integrand is holomorphic (analytic) within a region containing the closed contour C. The contour to be used for both integrals is shown in Fig. 5.2,
, provided that the integrand is holomorphic (analytic) within a region containing the closed contour C. The contour to be used for both integrals is shown in Fig. 5.2, 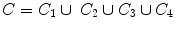 , and where
, and where 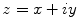 .
.
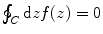 , provided that the integrand is holomorphic (analytic) within a region containing the closed contour C. The contour to be used for both integrals is shown in Fig. 5.2,
, provided that the integrand is holomorphic (analytic) within a region containing the closed contour C. The contour to be used for both integrals is shown in Fig. 5.2, 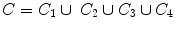 , and where
, and where 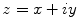 .
.Then, as the function 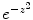 is holomorphic for this contour, the Cauchy–Goursat theorem gives
is holomorphic for this contour, the Cauchy–Goursat theorem gives
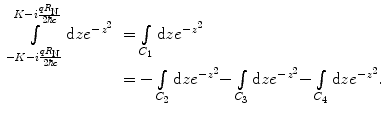
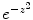 is holomorphic for this contour, the Cauchy–Goursat theorem gives
is holomorphic for this contour, the Cauchy–Goursat theorem gives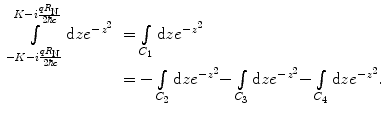
(5.29)
The integration over the contour C 2 is
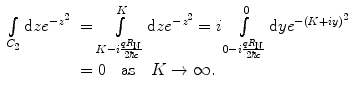
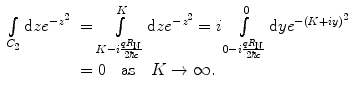
(5.30)
The integration over C 3 is
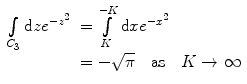
and that over C 4 is
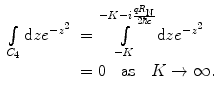
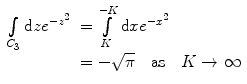
(5.31)
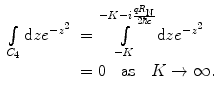
(5.32)
Combining these results gives
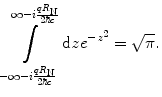
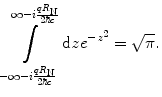
(5.33)
As before, the integrals over C 2 and C 4 will go to zero as 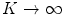 . The remaining integral (that over C 3) is solved by using the substitution of variable
. The remaining integral (that over C 3) is solved by using the substitution of variable 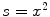 which yields
which yields 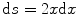 . Thus,
. Thus,
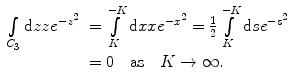
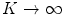 . The remaining integral (that over C 3) is solved by using the substitution of variable
. The remaining integral (that over C 3) is solved by using the substitution of variable 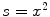 which yields
which yields 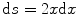 . Thus,
. Thus,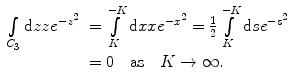
(5.35)
Hence,
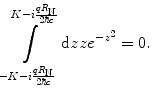
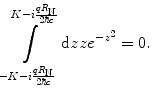
(5.36)
Finally, the substitution of this result into (5.24) yields the form factor for a Gaussian charge spatial distribution:
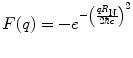
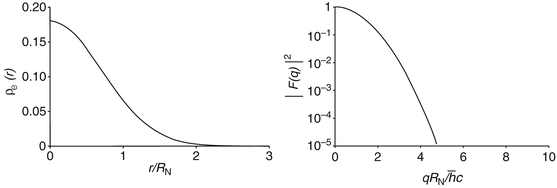
which is also Gaussian in q-space. Figure 5.3 shows the Gaussian spatial distribution and the modulus squared of the form factor. The smooth drop-off of  with r avoids diffraction effects in
with r avoids diffraction effects in  and a similarly smooth and monotonic drop-off is observed in momentum transfer space.
and a similarly smooth and monotonic drop-off is observed in momentum transfer space.
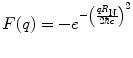
(5.39)
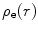 with r avoids diffraction effects in
with r avoids diffraction effects in 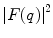 and a similarly smooth and monotonic drop-off is observed in momentum transfer space.
and a similarly smooth and monotonic drop-off is observed in momentum transfer space.
Fig. 5.3
Gaussian charge spatial distribution and corresponding squared modulus of the form factor
5.2.2.5 Exponential Charge Distribution
Another smoothly decreasing distribution with radius is that of the exponential charge distribution and which is described by
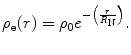
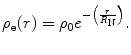
(5.40)
This distribution is an accurate representation of that of the proton. The normalisation constant is determined in the usual way:
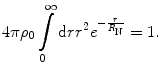
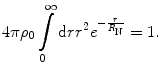
(5.41)
The integral is solved easily through two sequential integrations by parts to yield
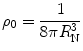
and the normalised exponential spatial charge distribution is thus
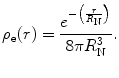
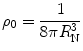
(5.42)
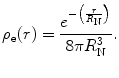
(5.43)
The integral of (5.44) is solved be rewriting it as
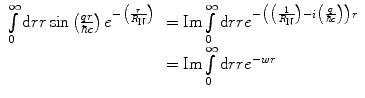
where 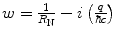 . Using the substitution of variable
. Using the substitution of variable 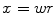 and following a subsequent integration by parts, the integration is
and following a subsequent integration by parts, the integration is
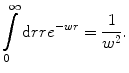
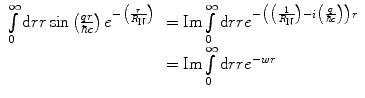
(5.45)
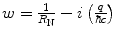 . Using the substitution of variable
. Using the substitution of variable 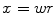 and following a subsequent integration by parts, the integration is
and following a subsequent integration by parts, the integration is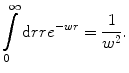
(5.46)
The resulting form factor for the exponential charge spatial distribution is
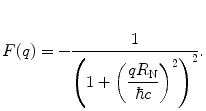
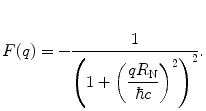
(5.48)
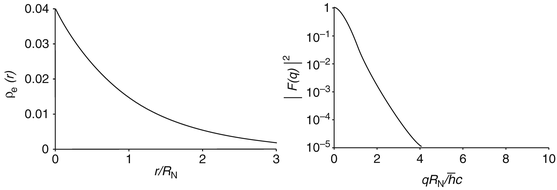
Figure 5.4 shows the exponential spatial distribution and the modulus squared of the form factor. As with the Gaussian distribution, the smooth drop-off of the exponential distribution yields a smooth drop-off in momentum transfer by  .
.
 .
.
Fig. 5.4
Exponential charge spatial distribution and corresponding modulus squared of the form factor
5.2.3 Summary of Nuclear Form Factors
It should be noted that the ordinates in all of the plots of 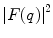 are logarithmic. This indicates, from (5.6), that the Coulomb scattering cross section for an extended target decreases more rapidly with momentum transfer/scattering angle than it does for a point target. As the abscissa of these plots is the dimensionless quantity,
are logarithmic. This indicates, from (5.6), that the Coulomb scattering cross section for an extended target decreases more rapidly with momentum transfer/scattering angle than it does for a point target. As the abscissa of these plots is the dimensionless quantity, 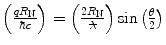 , small values of
, small values of 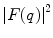 will correspond to forward scattering angles and reduced de Broglie wavelengths relative to scattering centre dimensions (i.e. high momentum transfer). Another target-dependent parameter to be specified is R N, which is the radius reflective of nuclear dimensions to be used in the evaluation of the form factor.
will correspond to forward scattering angles and reduced de Broglie wavelengths relative to scattering centre dimensions (i.e. high momentum transfer). Another target-dependent parameter to be specified is R N, which is the radius reflective of nuclear dimensions to be used in the evaluation of the form factor.
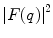 are logarithmic. This indicates, from (5.6), that the Coulomb scattering cross section for an extended target decreases more rapidly with momentum transfer/scattering angle than it does for a point target. As the abscissa of these plots is the dimensionless quantity,
are logarithmic. This indicates, from (5.6), that the Coulomb scattering cross section for an extended target decreases more rapidly with momentum transfer/scattering angle than it does for a point target. As the abscissa of these plots is the dimensionless quantity, 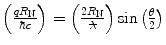 , small values of
, small values of 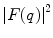 will correspond to forward scattering angles and reduced de Broglie wavelengths relative to scattering centre dimensions (i.e. high momentum transfer). Another target-dependent parameter to be specified is R N, which is the radius reflective of nuclear dimensions to be used in the evaluation of the form factor.
will correspond to forward scattering angles and reduced de Broglie wavelengths relative to scattering centre dimensions (i.e. high momentum transfer). Another target-dependent parameter to be specified is R N, which is the radius reflective of nuclear dimensions to be used in the evaluation of the form factor.In addition to the analytical forms shown above, the spatial distribution of the protons within the nucleus can be described by the Woods–Saxon, or Fermi, distribution:
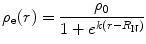
where 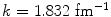 . The form factor for this distribution is a complicated expression given in terms of poly-logarithms of various orders (McParland 2010) and must be evaluated numerically. Another model of the nuclear charge distribution was presented by Helm (1956) and which treats the nuclear charge distribution as the convolution of two uniform distributions (5.11) or
. The form factor for this distribution is a complicated expression given in terms of poly-logarithms of various orders (McParland 2010) and must be evaluated numerically. Another model of the nuclear charge distribution was presented by Helm (1956) and which treats the nuclear charge distribution as the convolution of two uniform distributions (5.11) or
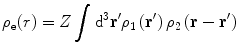
where the distributions are over two spheres of radii R 1 and R 2.
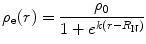
(5.49)
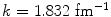 . The form factor for this distribution is a complicated expression given in terms of poly-logarithms of various orders (McParland 2010) and must be evaluated numerically. Another model of the nuclear charge distribution was presented by Helm (1956) and which treats the nuclear charge distribution as the convolution of two uniform distributions (5.11) or
. The form factor for this distribution is a complicated expression given in terms of poly-logarithms of various orders (McParland 2010) and must be evaluated numerically. Another model of the nuclear charge distribution was presented by Helm (1956) and which treats the nuclear charge distribution as the convolution of two uniform distributions (5.11) or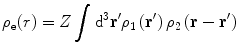
(5.50)
5.3 Screened Charges
5.3.1 Introduction
The previous consideration of a finite scattering centre introduced only one component of a realistic model of the atom to be used in the calculation of the elastic Coulomb scattering of a particle with high momentum and which has penetrated the atomic electrons surrounding the nucleus. The effect of ‘screening’, or the reduction of the effective electric charge of the nucleus by this electron cloud, as perceived by the projectile, is now to be reviewed.
In the discussions to follow, we will always consider the target atom to be both neutral (i.e. of atomic number Z and with Z bound electrons) and in its ground state. In this case, the effective interaction energy sensed by the projectile of charge ze incident to an atomic target with a nuclear charge Ze and an electron charge Ze is given by
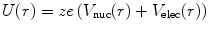
where 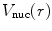 and
and 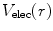 are the Coulomb potentials associated with the atomic nucleus and the distributed atomic electrons, respectively. The nuclear potential is given by the distributed-charge result of (5.2). For an electron density
are the Coulomb potentials associated with the atomic nucleus and the distributed atomic electrons, respectively. The nuclear potential is given by the distributed-charge result of (5.2). For an electron density 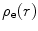 of atomic electrons per unit volume, we have the non-unity normalisation:
of atomic electrons per unit volume, we have the non-unity normalisation:
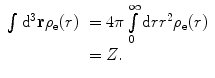
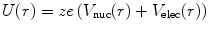
(5.51)
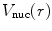 and
and 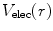 are the Coulomb potentials associated with the atomic nucleus and the distributed atomic electrons, respectively. The nuclear potential is given by the distributed-charge result of (5.2). For an electron density
are the Coulomb potentials associated with the atomic nucleus and the distributed atomic electrons, respectively. The nuclear potential is given by the distributed-charge result of (5.2). For an electron density 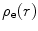 of atomic electrons per unit volume, we have the non-unity normalisation:
of atomic electrons per unit volume, we have the non-unity normalisation: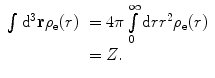
(5.52)
The electronic Coulomb potential can thus be written as
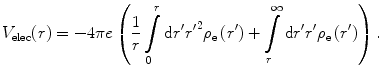
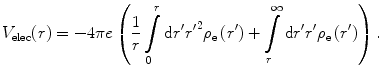
(5.53)
In order to focus this discussion on the screening by atomic electrons, we will treat the atomic nucleus as a point charge, i.e.
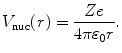
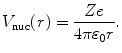
(5.54)
The combination of a finite nuclear charge distribution and screening is discussed in the next chapter.
Accounting for the effects of atomic electron screening, the effective Coulomb potential affecting the projectile is, in its most general form,
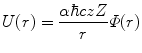
where the screening function 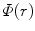 has the property
has the property ![$$ \varPhi (r)\in [0,1] $$](/wp-content/uploads/2016/04/A306762_1_En_5_Chapter_IEq000561.gif) and the limiting properties of
and the limiting properties of 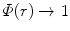 as
as 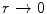 and
and 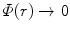 as
as 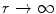 . The latter properties reflect the two cases of the projectile having penetrated the screening electrons and experiencing the nuclear Coulomb field alone or of being at an extended distance from the atom and feeling a zero Coulomb potential. Recall that these conditions are implicit to the target being a neutral atom. Hence, the effective nuclear charge beyond screening that is seen by the projectile is
. The latter properties reflect the two cases of the projectile having penetrated the screening electrons and experiencing the nuclear Coulomb field alone or of being at an extended distance from the atom and feeling a zero Coulomb potential. Recall that these conditions are implicit to the target being a neutral atom. Hence, the effective nuclear charge beyond screening that is seen by the projectile is 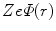 , i.e. it has an explicit dependence upon distance from the nucleus.
, i.e. it has an explicit dependence upon distance from the nucleus.
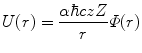
(5.55)
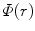 has the property
has the property ![$$ \varPhi (r)\in [0,1] $$](/wp-content/uploads/2016/04/A306762_1_En_5_Chapter_IEq000561.gif) and the limiting properties of
and the limiting properties of 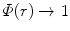 as
as 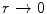 and
and 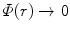 as
as 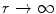 . The latter properties reflect the two cases of the projectile having penetrated the screening electrons and experiencing the nuclear Coulomb field alone or of being at an extended distance from the atom and feeling a zero Coulomb potential. Recall that these conditions are implicit to the target being a neutral atom. Hence, the effective nuclear charge beyond screening that is seen by the projectile is
. The latter properties reflect the two cases of the projectile having penetrated the screening electrons and experiencing the nuclear Coulomb field alone or of being at an extended distance from the atom and feeling a zero Coulomb potential. Recall that these conditions are implicit to the target being a neutral atom. Hence, the effective nuclear charge beyond screening that is seen by the projectile is 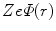 , i.e. it has an explicit dependence upon distance from the nucleus.
, i.e. it has an explicit dependence upon distance from the nucleus.In this section, we examine two approaches of accounting for the effects of atomic electron screening upon the elastic Coulomb scattering cross section for atomic targets:
The first assumes that the atomic electrons provide a continuous screen of the nuclear electrostatic potential so that the effective Coulomb potential can be modelled by the analytical form of the Wentzel type of potential (or, similarly, that of Debye and Hückel), which is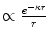 , or by a numerical result derived from the Thomas–Fermi statistical model of the atom. Both of these results yield expressions for the Coulomb differential cross section, which provide a finite screening angle limiting the cross section to a finite value as the scattering angle
, or by a numerical result derived from the Thomas–Fermi statistical model of the atom. Both of these results yield expressions for the Coulomb differential cross section, which provide a finite screening angle limiting the cross section to a finite value as the scattering angle 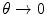 .
.
The second calculation instead treats the atomic electrons as being discrete electric charges and evaluates their effect upon the scattering by using quantum perturbation theory from a net Coulomb potential given by the sum of that of a point nucleus and the individual contributions of the Z electrons. The result is an elastic form factor expression which also maintains a finite result for the Coulomb elastic scatter cross section as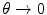 and replicates that of the continuous-screening calculation.
and replicates that of the continuous-screening calculation.
Using our results derived for continuous screening, we examine the various conditions of screening and the effects that they have upon the angular distribution of the screened Coulomb elastic scatter differential cross section.
5.3.2 Continuous Screening Part I: Exponential Screening
The derivation of the unscreened cross section given by (4.78) began with the calculation of the scattering amplitude (to the first order of the Born expansion) for an exponential modification of the Coulomb potential between a projectile of charge ze and a target of charge Ze, such that the interaction energy is
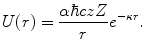
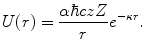
(5.56)
Using this as an approximate model of atomic electron screening, from (5.55), the screening function is
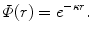
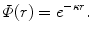
(5.57)
In the original evaluation of the unscreened cross section, κ was treated as a calculation tool in the evaluation of the scattering amplitude and then allowed to go to zero, following the integration of (4.76). Here, we shall instead treat 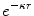 as a continuous-screening term which approximates the moderation of the nuclear Coulomb potential by the surrounding atomic electrons and retain it within the calculation as a result. Thus, the spatial variation of the effect of screening is described by a single-atomic electron screening parameter,
as a continuous-screening term which approximates the moderation of the nuclear Coulomb potential by the surrounding atomic electrons and retain it within the calculation as a result. Thus, the spatial variation of the effect of screening is described by a single-atomic electron screening parameter, 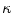 . Equation (4.76) is rewritten as
. Equation (4.76) is rewritten as
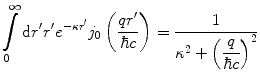
and the scattering amplitude (to the first order of the Born expansion) is
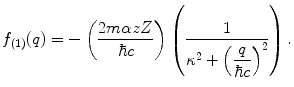
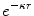 as a continuous-screening term which approximates the moderation of the nuclear Coulomb potential by the surrounding atomic electrons and retain it within the calculation as a result. Thus, the spatial variation of the effect of screening is described by a single-atomic electron screening parameter,
as a continuous-screening term which approximates the moderation of the nuclear Coulomb potential by the surrounding atomic electrons and retain it within the calculation as a result. Thus, the spatial variation of the effect of screening is described by a single-atomic electron screening parameter, 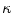 . Equation (4.76) is rewritten as
. Equation (4.76) is rewritten as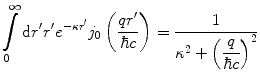
(5.58)
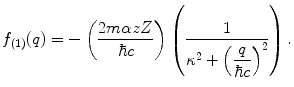
(5.59)
The screened differential cross section in solid angle, which we recall is proportional to the modulus squared of the scattering amplitude, can be written as, using the definitions of the Bohr collision diameter 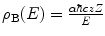 , the reduced de Broglie wavelength
, the reduced de Broglie wavelength 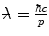 and the relationship between the elastic momentum transfer and scattering angle,
and the relationship between the elastic momentum transfer and scattering angle, 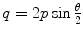 :
:
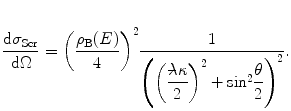
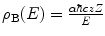 , the reduced de Broglie wavelength
, the reduced de Broglie wavelength 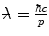 and the relationship between the elastic momentum transfer and scattering angle,
and the relationship between the elastic momentum transfer and scattering angle, 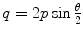 :
: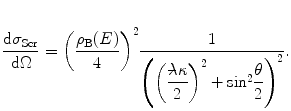
(5.60)
As our interest of the effects of atomic electron screening will be in the divergence of the cross section at small scattering angles, we can invoke the small-angle approximation of 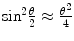 to give4
to give4
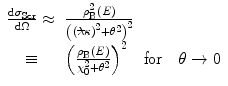
where the screening angle 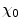 is defined as the product of the atomic electron screening parameter and the de Broglie wavelength:
is defined as the product of the atomic electron screening parameter and the de Broglie wavelength:
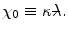
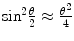 to give4
to give4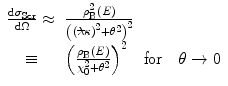
(5.61)
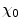 is defined as the product of the atomic electron screening parameter and the de Broglie wavelength:
is defined as the product of the atomic electron screening parameter and the de Broglie wavelength: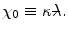
(5.62)
Clearly, the divergence of the differential cross section at 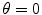 has now been avoided through the inclusion of screening and the resulting calculated cross section at
has now been avoided through the inclusion of screening and the resulting calculated cross section at 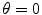




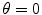 has now been avoided through the inclusion of screening and the resulting calculated cross section at
has now been avoided through the inclusion of screening and the resulting calculated cross section at 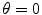
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree