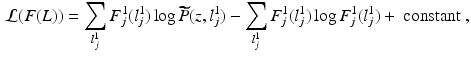Fig. 1.
(a) Real-world fluorescence microscopy images 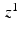 (top) and
(top) and 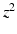 (bottom), depict the presence of protein and cell nuclei, respectively. (b) Proposed Probabilistic Graphical Model for Colocalization Estimation. Filled circles denote observed image data
(bottom), depict the presence of protein and cell nuclei, respectively. (b) Proposed Probabilistic Graphical Model for Colocalization Estimation. Filled circles denote observed image data 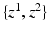 . Label images
. Label images 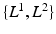 are hidden random variables. We estimate all parameters
are hidden random variables. We estimate all parameters 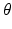 from data. The nature and strength of colocalization is modeled by parameter
from data. The nature and strength of colocalization is modeled by parameter 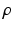 . Parameters
. Parameters 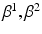 model spatial smoothness of the labels in
model spatial smoothness of the labels in 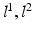 . In this paper, for simplicity, we use a single
. In this paper, for simplicity, we use a single 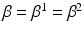 . Means and standard deviations
. Means and standard deviations 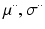 model image intensities of objects and backgrounds in
model image intensities of objects and backgrounds in 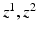 . (c) MAP label images
. (c) MAP label images 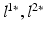 , indicating object presence /absence, computed after optimal parameters
, indicating object presence /absence, computed after optimal parameters 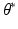 are found by VBEM. Note: this paper focuses on estimating colocalization
are found by VBEM. Note: this paper focuses on estimating colocalization 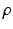 using VBEM, which is crucial to several clinical and scientific studies; the MAP label images are unused by VBEM and are shown only to provide additional insights into the proposed approach.
using VBEM, which is crucial to several clinical and scientific studies; the MAP label images are unused by VBEM and are shown only to provide additional insights into the proposed approach.
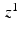 (top) and
(top) and 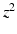 (bottom), depict the presence of protein and cell nuclei, respectively. (b) Proposed Probabilistic Graphical Model for Colocalization Estimation. Filled circles denote observed image data
(bottom), depict the presence of protein and cell nuclei, respectively. (b) Proposed Probabilistic Graphical Model for Colocalization Estimation. Filled circles denote observed image data 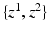 . Label images
. Label images 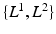 are hidden random variables. We estimate all parameters
are hidden random variables. We estimate all parameters 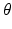 from data. The nature and strength of colocalization is modeled by parameter
from data. The nature and strength of colocalization is modeled by parameter 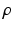 . Parameters
. Parameters 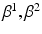 model spatial smoothness of the labels in
model spatial smoothness of the labels in 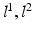 . In this paper, for simplicity, we use a single
. In this paper, for simplicity, we use a single 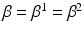 . Means and standard deviations
. Means and standard deviations 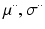 model image intensities of objects and backgrounds in
model image intensities of objects and backgrounds in 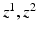 . (c) MAP label images
. (c) MAP label images 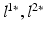 , indicating object presence /absence, computed after optimal parameters
, indicating object presence /absence, computed after optimal parameters 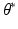 are found by VBEM. Note: this paper focuses on estimating colocalization
are found by VBEM. Note: this paper focuses on estimating colocalization 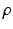 using VBEM, which is crucial to several clinical and scientific studies; the MAP label images are unused by VBEM and are shown only to provide additional insights into the proposed approach.
using VBEM, which is crucial to several clinical and scientific studies; the MAP label images are unused by VBEM and are shown only to provide additional insights into the proposed approach.Let 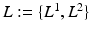 denote a random field modeling the pixel labels of the two objects. Specifically, let
denote a random field modeling the pixel labels of the two objects. Specifically, let 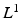 be a binary label image with I pixels
be a binary label image with I pixels 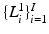 with possible label values
with possible label values 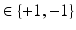 , where
, where 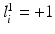 indicates the object’s presence at pixel i in
indicates the object’s presence at pixel i in 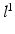 ; similarly,
; similarly, 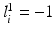 indicates the object’s absence at pixel i in
indicates the object’s absence at pixel i in 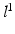 . We follow similar notations and semantics for
. We follow similar notations and semantics for 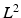 . We assume that the spatial distributions of objects are (i) smooth within each image and (ii) codependent between images. To model these properties, each pixel has intra-image and inter-image neighbors.
. We assume that the spatial distributions of objects are (i) smooth within each image and (ii) codependent between images. To model these properties, each pixel has intra-image and inter-image neighbors.
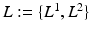 denote a random field modeling the pixel labels of the two objects. Specifically, let
denote a random field modeling the pixel labels of the two objects. Specifically, let 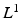 be a binary label image with I pixels
be a binary label image with I pixels 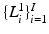 with possible label values
with possible label values 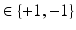 , where
, where 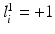 indicates the object’s presence at pixel i in
indicates the object’s presence at pixel i in 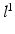 ; similarly,
; similarly, 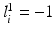 indicates the object’s absence at pixel i in
indicates the object’s absence at pixel i in 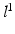 . We follow similar notations and semantics for
. We follow similar notations and semantics for 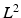 . We assume that the spatial distributions of objects are (i) smooth within each image and (ii) codependent between images. To model these properties, each pixel has intra-image and inter-image neighbors.
. We assume that the spatial distributions of objects are (i) smooth within each image and (ii) codependent between images. To model these properties, each pixel has intra-image and inter-image neighbors.We introduce a neighborhood system 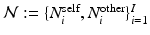 , where
, where 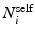 and
and 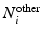 denote sets of neighbors of pixel i in the same image (to which pixel i belongs) and the other image, respectively. To have isotropic neighborhoods, we employ Gaussian-weighted masks w where the ij-th element
denote sets of neighbors of pixel i in the same image (to which pixel i belongs) and the other image, respectively. To have isotropic neighborhoods, we employ Gaussian-weighted masks w where the ij-th element 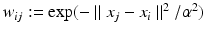 , where
, where 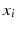 and
and 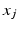 are physical coordinates of pixels i and j, respectively. We use two such masks, i.e.,
are physical coordinates of pixels i and j, respectively. We use two such masks, i.e., 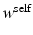 (for intra-image smoothness) and
(for intra-image smoothness) and  (for inter-image colocalization) with underlying parameters
(for inter-image colocalization) with underlying parameters 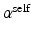 and
and  , respectively. We set
, respectively. We set 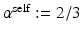 pixels to restrict the neighborhood to 2 neighbors along each dimension (we restrict the neighborhood so that
pixels to restrict the neighborhood to 2 neighbors along each dimension (we restrict the neighborhood so that  to be large enough to be able to model the longest-range direct spatial interactions between the biological entities; this is application dependent and informed by prior knowledge, but the results are fairly robust to the choice of this parameter. In this paper,
to be large enough to be able to model the longest-range direct spatial interactions between the biological entities; this is application dependent and informed by prior knowledge, but the results are fairly robust to the choice of this parameter. In this paper, 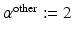 pixels.
pixels.
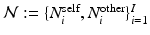 , where
, where 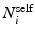 and
and 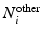 denote sets of neighbors of pixel i in the same image (to which pixel i belongs) and the other image, respectively. To have isotropic neighborhoods, we employ Gaussian-weighted masks w where the ij-th element
denote sets of neighbors of pixel i in the same image (to which pixel i belongs) and the other image, respectively. To have isotropic neighborhoods, we employ Gaussian-weighted masks w where the ij-th element 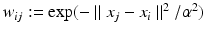 , where
, where 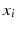 and
and 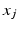 are physical coordinates of pixels i and j, respectively. We use two such masks, i.e.,
are physical coordinates of pixels i and j, respectively. We use two such masks, i.e., 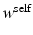 (for intra-image smoothness) and
(for intra-image smoothness) and  (for inter-image colocalization) with underlying parameters
(for inter-image colocalization) with underlying parameters 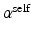 and
and  , respectively. We set
, respectively. We set 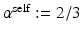 pixels to restrict the neighborhood to 2 neighbors along each dimension (we restrict the neighborhood so that
pixels to restrict the neighborhood to 2 neighbors along each dimension (we restrict the neighborhood so that  to be large enough to be able to model the longest-range direct spatial interactions between the biological entities; this is application dependent and informed by prior knowledge, but the results are fairly robust to the choice of this parameter. In this paper,
to be large enough to be able to model the longest-range direct spatial interactions between the biological entities; this is application dependent and informed by prior knowledge, but the results are fairly robust to the choice of this parameter. In this paper, 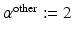 pixels.
pixels.We model the prior probability mass function (PMF) of the label image pair L as
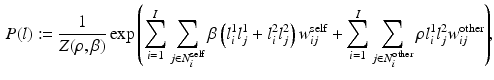
where the normalization constant (partition function) 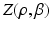 is a function of the smoothness parameter
is a function of the smoothness parameter 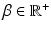 and the colocalization parameter
and the colocalization parameter 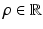 . The motivation for this model is as follows. The terms involving
. The motivation for this model is as follows. The terms involving 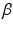 are derived from a standard Ising model of smoothness on the label images. The term involving
are derived from a standard Ising model of smoothness on the label images. The term involving 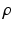 is novel and carefully designed as follows. First,
is novel and carefully designed as follows. First, 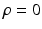 decouples the two label images such that P (l) can be written as
decouples the two label images such that P (l) can be written as 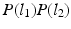 ; this indicates absence of colocalization. Second, because the labels are designed to be
; this indicates absence of colocalization. Second, because the labels are designed to be 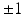 , a positive
, a positive 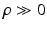 forces the interacting labels in the two images
forces the interacting labels in the two images 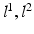 (i.e., labels in neighborhoods of each other) towards being equal (i.e., both
(i.e., labels in neighborhoods of each other) towards being equal (i.e., both 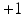 or both
or both 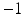 ) to produce a high label image probability. This implies that the neighboring labels in the two images both likely indicate the presence of the objects or both indicate the absence of the objects. Third, similarly, a negative
) to produce a high label image probability. This implies that the neighboring labels in the two images both likely indicate the presence of the objects or both indicate the absence of the objects. Third, similarly, a negative 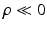 forces the interacting labels in the two images to be negative of each other, i.e., the presence of the object on one image indicates the absence of the other object in the other image.
forces the interacting labels in the two images to be negative of each other, i.e., the presence of the object on one image indicates the absence of the other object in the other image.
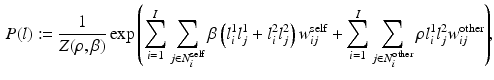
(1)
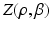 is a function of the smoothness parameter
is a function of the smoothness parameter 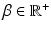 and the colocalization parameter
and the colocalization parameter 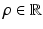 . The motivation for this model is as follows. The terms involving
. The motivation for this model is as follows. The terms involving 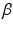 are derived from a standard Ising model of smoothness on the label images. The term involving
are derived from a standard Ising model of smoothness on the label images. The term involving 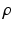 is novel and carefully designed as follows. First,
is novel and carefully designed as follows. First, 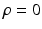 decouples the two label images such that P (l) can be written as
decouples the two label images such that P (l) can be written as 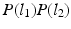 ; this indicates absence of colocalization. Second, because the labels are designed to be
; this indicates absence of colocalization. Second, because the labels are designed to be 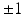 , a positive
, a positive 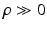 forces the interacting labels in the two images
forces the interacting labels in the two images 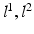 (i.e., labels in neighborhoods of each other) towards being equal (i.e., both
(i.e., labels in neighborhoods of each other) towards being equal (i.e., both 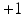 or both
or both 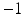 ) to produce a high label image probability. This implies that the neighboring labels in the two images both likely indicate the presence of the objects or both indicate the absence of the objects. Third, similarly, a negative
) to produce a high label image probability. This implies that the neighboring labels in the two images both likely indicate the presence of the objects or both indicate the absence of the objects. Third, similarly, a negative 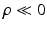 forces the interacting labels in the two images to be negative of each other, i.e., the presence of the object on one image indicates the absence of the other object in the other image.
forces the interacting labels in the two images to be negative of each other, i.e., the presence of the object on one image indicates the absence of the other object in the other image.Let 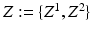 denote a random field modeling the intensities of the two objects and the backgrounds. We assume that the intensities of each object are Gaussian distributed as a result of natural intensity variation, partial-volume effects, minor shading artifacts, etc. We assume that the data is corrupted by i.i.d. additive Gaussian noise. Let the intensities of the object and the background in the observed image
denote a random field modeling the intensities of the two objects and the backgrounds. We assume that the intensities of each object are Gaussian distributed as a result of natural intensity variation, partial-volume effects, minor shading artifacts, etc. We assume that the data is corrupted by i.i.d. additive Gaussian noise. Let the intensities of the object and the background in the observed image 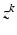 , where
, where 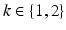 , be Gaussian distributed with parameters
, be Gaussian distributed with parameters 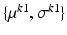 and
and 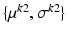 , respectively. Then, the likelihood of observing data z, given labels l, is
, respectively. Then, the likelihood of observing data z, given labels l, is
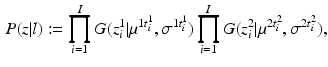
where 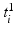 maps the label value
maps the label value 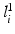 to the object number, i.e.,
to the object number, i.e., 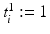 if
if 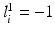 and
and 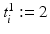 if
if 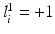 ; similarly for
; similarly for 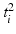 .
.
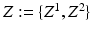 denote a random field modeling the intensities of the two objects and the backgrounds. We assume that the intensities of each object are Gaussian distributed as a result of natural intensity variation, partial-volume effects, minor shading artifacts, etc. We assume that the data is corrupted by i.i.d. additive Gaussian noise. Let the intensities of the object and the background in the observed image
denote a random field modeling the intensities of the two objects and the backgrounds. We assume that the intensities of each object are Gaussian distributed as a result of natural intensity variation, partial-volume effects, minor shading artifacts, etc. We assume that the data is corrupted by i.i.d. additive Gaussian noise. Let the intensities of the object and the background in the observed image 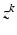 , where
, where 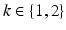 , be Gaussian distributed with parameters
, be Gaussian distributed with parameters 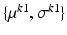 and
and 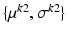 , respectively. Then, the likelihood of observing data z, given labels l, is
, respectively. Then, the likelihood of observing data z, given labels l, is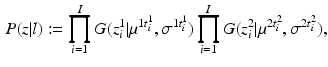
(2)
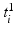 maps the label value
maps the label value 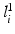 to the object number, i.e.,
to the object number, i.e., 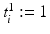 if
if 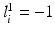 and
and 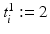 if
if 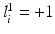 ; similarly for
; similarly for 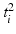 .
.Let the set of parameters be 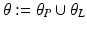 , where the prior parameters are
, where the prior parameters are 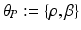 and the likelihood parameters are
and the likelihood parameters are 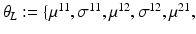
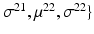 . We propose to formulate colocalization estimation as the following maximum-a-posteriori Bayesian estimation problem over all parameters
. We propose to formulate colocalization estimation as the following maximum-a-posteriori Bayesian estimation problem over all parameters 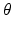 :
:
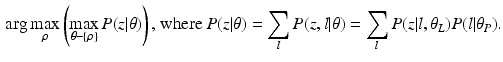
A novelty in our approach is that we estimate 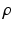 (as well as
(as well as 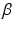 ) automatically from the data. We observe that the optimization of the parameters
) automatically from the data. We observe that the optimization of the parameters 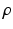 and
and 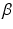 is non-trivial because of their involvement in the partition function
is non-trivial because of their involvement in the partition function 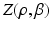 that is intractable to evaluate. Furthermore, we optimize all parameters underlying the model directly from the data.
that is intractable to evaluate. Furthermore, we optimize all parameters underlying the model directly from the data.
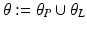 , where the prior parameters are
, where the prior parameters are 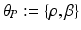 and the likelihood parameters are
and the likelihood parameters are 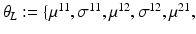
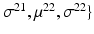 . We propose to formulate colocalization estimation as the following maximum-a-posteriori Bayesian estimation problem over all parameters
. We propose to formulate colocalization estimation as the following maximum-a-posteriori Bayesian estimation problem over all parameters 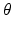 :
: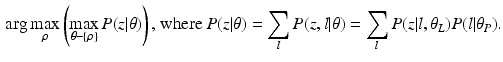
(3)
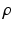 (as well as
(as well as 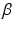 ) automatically from the data. We observe that the optimization of the parameters
) automatically from the data. We observe that the optimization of the parameters 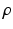 and
and 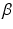 is non-trivial because of their involvement in the partition function
is non-trivial because of their involvement in the partition function 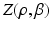 that is intractable to evaluate. Furthermore, we optimize all parameters underlying the model directly from the data.
that is intractable to evaluate. Furthermore, we optimize all parameters underlying the model directly from the data.3.2 Expectation Maximization for Parameter Estimation
We treat the labels L as hidden variables and solve the parameter-estimation problem using EM. EM is an iterative optimization algorithm, each iteration comprising an E step and an M step. Consider that after iteration n, the parameter estimate is 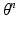 . Then, in iteration
. Then, in iteration 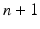 , the updated parameter estimate
, the updated parameter estimate 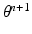 is obtained as follows.
is obtained as follows.
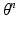 . Then, in iteration
. Then, in iteration 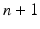 , the updated parameter estimate
, the updated parameter estimate 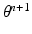 is obtained as follows.
is obtained as follows.The E step involves constructing the 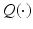 function
function
![$$\begin{aligned} Q (\theta ; \theta ^n) := E_{P (L | z, \theta ^n)} [ \log P (z,L | \theta ) ] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_1_Chapter_Equ4.gif)
that is intractable to evaluate analytically. Furthermore, a Monte-Carlo simulation-based approximation of the expectation leads to challenges in reliable and efficient sampling; e.g., while Gibbs sampling of the label fields is computationally expensive, determining an appropriate burn-in period and detecting convergence of the Gibbs sampler pose serious theoretical challenges. Thus, we opt for variational inference and choose to approximate the posterior PMF 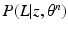 by a factorizable analytical model
by a factorizable analytical model
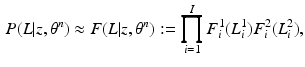
where we optimize the per-pixel factors, i.e., PMFs, 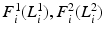 to best fit the posterior. This factorized approximation for the posterior makes the
to best fit the posterior. This factorized approximation for the posterior makes the 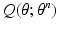 function more tractable. We describe this strategy in the next section.
function more tractable. We describe this strategy in the next section.
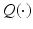 function
function![$$\begin{aligned} Q (\theta ; \theta ^n) := E_{P (L | z, \theta ^n)} [ \log P (z,L | \theta ) ] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_1_Chapter_Equ4.gif)
(4)
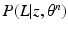 by a factorizable analytical model
by a factorizable analytical model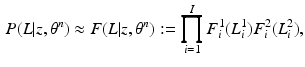
(5)
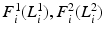 to best fit the posterior. This factorized approximation for the posterior makes the
to best fit the posterior. This factorized approximation for the posterior makes the 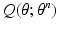 function more tractable. We describe this strategy in the next section.
function more tractable. We describe this strategy in the next section.The M step subsequently maximizes the 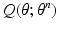 function over parameters
function over parameters 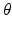 . The E and M steps are repeated until convergence; we observe that a few iterations are suffice.
. The E and M steps are repeated until convergence; we observe that a few iterations are suffice.
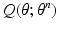 function over parameters
function over parameters 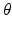 . The E and M steps are repeated until convergence; we observe that a few iterations are suffice.
. The E and M steps are repeated until convergence; we observe that a few iterations are suffice.3.3 E Step: Variational Inference of the Factorized Posterior
Within each EM iteration, we use variational inference to optimize the factors underlying 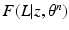 . To simplify notation, we omit
. To simplify notation, we omit 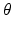 where it is obvious. We rewrite
where it is obvious. We rewrite
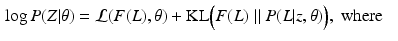
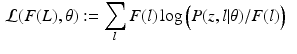
and 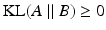 denotes the Kullback-Leibler (KL) divergence between distributions A and B. Our goal is to find the maximal lower bound
denotes the Kullback-Leibler (KL) divergence between distributions A and B. Our goal is to find the maximal lower bound 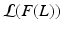 of the data log-probability
of the data log-probability 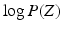 , under the factorization constraint on F(L). We do this by maximizing
, under the factorization constraint on F(L). We do this by maximizing 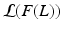 , because
, because 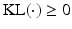 guarantees
guarantees 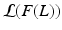 to be a lower bound. We perform this functional optimization by iterative optimization of each of the factor functions; this is possible because the factors are designed to be independent of each other. We now incorporate the factorized form of F(L) and, without loss of generality, separate terms involving
to be a lower bound. We perform this functional optimization by iterative optimization of each of the factor functions; this is possible because the factors are designed to be independent of each other. We now incorporate the factorized form of F(L) and, without loss of generality, separate terms involving 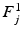 from the other terms. This yields
from the other terms. This yields
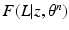 . To simplify notation, we omit
. To simplify notation, we omit 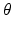 where it is obvious. We rewrite
where it is obvious. We rewrite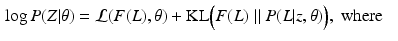
(6)
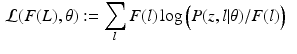
(7)
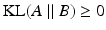 denotes the Kullback-Leibler (KL) divergence between distributions A and B. Our goal is to find the maximal lower bound
denotes the Kullback-Leibler (KL) divergence between distributions A and B. Our goal is to find the maximal lower bound 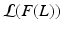 of the data log-probability
of the data log-probability 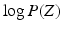 , under the factorization constraint on F(L). We do this by maximizing
, under the factorization constraint on F(L). We do this by maximizing 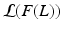 , because
, because 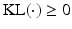 guarantees
guarantees 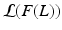 to be a lower bound. We perform this functional optimization by iterative optimization of each of the factor functions; this is possible because the factors are designed to be independent of each other. We now incorporate the factorized form of F(L) and, without loss of generality, separate terms involving
to be a lower bound. We perform this functional optimization by iterative optimization of each of the factor functions; this is possible because the factors are designed to be independent of each other. We now incorporate the factorized form of F(L) and, without loss of generality, separate terms involving 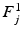 from the other terms. This yields
from the other terms. This yields