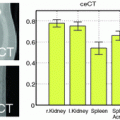
if both exact and one-off predictions are considered correct.
1 Introduction
Systems for storing and transmitting digital data are increasing rapidly in size and bandwidth capacity. Data collection projects such as COPDGene (19,000 lung CT scans of 10,000 subjects) [1] offer unprecedented opportunities to learn from large medical image sets, for example to discover subtle aspects of anatomy or pathology only observable in subsets of the population. For this, image processing algorithms must scale with the quantities of available data.
Consider an algorithm designed to discover and characterize unknown clinical phenotypes or disease subclasses from a large set of N images. Two major challenges that must be addressed are computational complexity and robust statistical inference. The fundamental operation required is often image-to-image similarity evaluation, which incurs a prohibitive computational complexity cost of O(N) when performed via traditional pair-wise methods such as registration [2, 3] or feature matching [4, 5]. For example, computing the pairwise affinity matrix between 416 low resolution brain scans via efficient deformable registration requires about one week on a 50 GHz cluster computer [2]. Furthermore, robustly estimating variables of interest requires coping with myriad confounds, including arbitrarily misaligned data, missing data due to resection or variable scan cropping (e.g. in order to reduce ionizing radiation exposure), inter-subject anatomical variability including abnormality, intra-subject variability due to growth and deformation (e.g. lung breathing state), inter-scanner variability in multi-site data, to name a few.
The technical contribution of this paper is a computational framework that provides a solution to both of these challenges. The framework is closely linked to large-scale data search methods where data are stored and indexed via nearest neighbor (NN) queries [6, 10]. Images are represented as collections of distinctive 3D scale-invariant features [7, 8], information-rich observations of salient image content. Robust, local image-to-image similarity is computed efficiently in O(log N) computational complexity via approximate nearest neighbor search.
The theoretical contribution is a novel estimator for class-conditional densities in a Naive Bayes classification formulation, representing a hybrid of kernel density [11] and KNN [12] methods. A mixture density is estimated for each input feature of a new image as the weighted sum of (1) a variable bandwidth kernel density computed from a set of nearest neighbors and (2) a background distribution over unrelated features. This estimator achieves state-of-the-art performance in automatically predicting the 5-class GOLD severity label from a large multi-site data set, improving upon previous results based on lung-specific image processing pipelines and single-site data [13, 28, 29]. Furthermore, subject-level classification is used to identify all instances duplicate subjects in a large set of 19,000 subjects, despite deformation due to breathing state.
2 Related Work
Our work derives from two main bodies of research, local invariant image feature methods and density estimation. Here, a local feature refers to a salient image patch or region identified via an interest operator, e.g. extrema of the difference-of-Gaussian operator in the popular scale-invariant feature transform (SIFT) [7]. Local features effectively serve as a reduced set of information-rich image content that enable highly efficient image processing algorithms, for example feature correspondence in O(log N) computational complexity via fast approximate NN search methods [9, 10]. Early feature detection methods identified salient image locations [14], scale-space theory [15] lead to the development of so-called scale-invariant [7] and affine-invariant [16] feature detection methods capable of repeatedly detecting the same image pattern despite global similarity and affine image transforms, in addition to intensity variations.
Once detected, salient image regions are cropped and spatially normalized to patches of size D voxels, then encoded as compact, highly distinctive descriptors for efficient indexing, e.g. the gradient orientation histogram (GoH) representation [7]. Note that there is a tradeoff between the patch dimension D and the number of unique samples available to populate the space of image patches 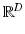 . At one extreme, voxel-size patches lead to a densely sampled but relatively uninformative
. At one extreme, voxel-size patches lead to a densely sampled but relatively uninformative 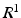 space, while at the other extreme, entire images provide an information-rich but severely under-sampled
space, while at the other extreme, entire images provide an information-rich but severely under-sampled 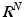 space. Intermediately-sized observations have been shown to be most effective for tasks such as classification [17]. Note also that many patches are rarely observed in natural medical images, and the typical set of patches is concentrated within a subspace or manifold
space. Intermediately-sized observations have been shown to be most effective for tasks such as classification [17]. Note also that many patches are rarely observed in natural medical images, and the typical set of patches is concentrated within a subspace or manifold 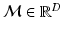 . Furthermore, local saliency operators further restrict the manifold to a subset of highly informative patches
. Furthermore, local saliency operators further restrict the manifold to a subset of highly informative patches 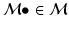 , as common, uninformative image patterns are not detected, e.g. non-localizable boundary structures or regions of homogenous image intensity.
, as common, uninformative image patterns are not detected, e.g. non-localizable boundary structures or regions of homogenous image intensity.
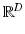 . At one extreme, voxel-size patches lead to a densely sampled but relatively uninformative
. At one extreme, voxel-size patches lead to a densely sampled but relatively uninformative 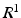 space, while at the other extreme, entire images provide an information-rich but severely under-sampled
space, while at the other extreme, entire images provide an information-rich but severely under-sampled 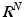 space. Intermediately-sized observations have been shown to be most effective for tasks such as classification [17]. Note also that many patches are rarely observed in natural medical images, and the typical set of patches is concentrated within a subspace or manifold
space. Intermediately-sized observations have been shown to be most effective for tasks such as classification [17]. Note also that many patches are rarely observed in natural medical images, and the typical set of patches is concentrated within a subspace or manifold 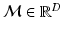 . Furthermore, local saliency operators further restrict the manifold to a subset of highly informative patches
. Furthermore, local saliency operators further restrict the manifold to a subset of highly informative patches 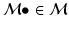 , as common, uninformative image patterns are not detected, e.g. non-localizable boundary structures or regions of homogenous image intensity.
, as common, uninformative image patterns are not detected, e.g. non-localizable boundary structures or regions of homogenous image intensity.Salient image content can thus be modeled as a set of local features, e.g. within a spatial configuration or as an unordered bag-of-features representation when inter-feature spatial relationships are difficult to model. Probabilistic models for inference typically require estimating densities from feature data. Non-parametric density estimators such as KDE or KNN estimators are particularly useful as an explicit model of the joint distribution is not required. They can be computed on-the-fly without requiring computationally expensive training, e.g. via instance-based or lazy-learning methods [13, 18, 19]. KDE seeks to quantify density from kernel functions centered around training samples [11, 20], whereas KNN estimators seek to quantify the density at a point from a set of K nearest neighbor samples [12, 13, 18, 19]. An interesting property of KNN estimators is that when used in classification, their prediction error is asymptotically upper bounded by no more than twice the optimal Bayes error rate as the number of data grow [12]. This property is particularly relevant given the increasing size of medical image data sets.
In the context of medical image analysis, scale-invariant features have been used to align and classify 3D medical image data [8, 21, 22], however they have not yet been adapted to large-scale indexing and inference. Although our work here focuses on inference, the feature-based correspondence framework is generally related to medical image analysis methods using nearest neighbors or proximity graphs across image data, including subject-level recognition [5], manifold learning [2, 3, 23], in particular methods based on local image characteristics [24, 25] and multi-atlas labeling [26].
The experimental portion of this paper investigates chronic pulmonary obstructive disorder (COPD) in a large set of multi-site lung CT images. A primary focus of COPD imaging research has been to characterize and classify disease phenotypes. Song et al. investigate various 2D feature descriptors for classifying lung tissues including local binary patterns and gradient orientation histograms [27]. Several authors propose subject-level COPD prediction as an avenue of exploratory research. Sorensen et al. [13] use texture patches in a binary classification COPD = (0,1) scenario on single-site data to achieve an area-under-the-curve (AUC) classification of 0.71. Mets et al. [28] use densitometric measures computed from single-site data of 1100 male subjects, to achieve an AUC value of 0.83 for binary COPD classification. Gu et al. [29] use automatic lung segmentation and densitometric measures to classify single-site data according to the GOLD range, achieving an exact classification rate of 0.37, or 0.83 if classification into neighboring categories is considered correct. A major challenge is classifying multi-site data acquired across different sites and scanners. On a large multi-site data set, our method achieves exact and one-off classification rates of 0.48 and 0.89, respectively, which to our knowledge are the highest rates reported for GOLD classification.
3 Method
3.1 Estimating Class Probabilities
Let 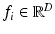 be a D-dimensional vector encoding the appearance of a scale-normalized image patch, e.g. a scale-invariant feature descriptor, and let
be a D-dimensional vector encoding the appearance of a scale-normalized image patch, e.g. a scale-invariant feature descriptor, and let 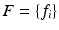 be a set of such features extracted in an image. Let C be a clinical variable of interest, e.g. a discrete measure of disease severity, defined over a set of M values
be a set of such features extracted in an image. Let C be a clinical variable of interest, e.g. a discrete measure of disease severity, defined over a set of M values ![$$[1,\dots ,m]$$](/wp-content/uploads/2016/09/A339424_1_En_26_Chapter_IEq9.gif) . Finally let
. Finally let 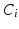 represent the value of C associated with feature
represent the value of C associated with feature 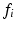 .
.
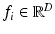 be a D-dimensional vector encoding the appearance of a scale-normalized image patch, e.g. a scale-invariant feature descriptor, and let
be a D-dimensional vector encoding the appearance of a scale-normalized image patch, e.g. a scale-invariant feature descriptor, and let 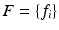 be a set of such features extracted in an image. Let C be a clinical variable of interest, e.g. a discrete measure of disease severity, defined over a set of M values
be a set of such features extracted in an image. Let C be a clinical variable of interest, e.g. a discrete measure of disease severity, defined over a set of M values ![$$[1,\dots ,m]$$](/wp-content/uploads/2016/09/A339424_1_En_26_Chapter_IEq9.gif) . Finally let
. Finally let 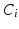 represent the value of C associated with feature
represent the value of C associated with feature 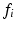 .
.We seek the posterior probability p(C|F) of clinical variable C conditioned on feature data F extracted in a query image, which can be expressed as
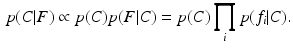
In Eq. (1), the first equality follows from Bayes’ rule, and the second from the so-called Naive Bayes assumption of conditional feature independence. This strong assumption is often made for computational convenience when modeling the true joint distribution over all features F is intractable. Nevertheless, it often leads to robust, effective modeling even in contexts where conditional independence does not strictly hold. Conditional independence is reasonable in the case of local image observations 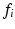 , as patches separated in scale and space do not typically exhibit direct correlations. On the RHS of Eq. (1), p(C) is a prior distribution over the clinical variable of interest C, and
, as patches separated in scale and space do not typically exhibit direct correlations. On the RHS of Eq. (1), p(C) is a prior distribution over the clinical variable of interest C, and 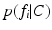 is the likelihood function of C associated with observed image feature
is the likelihood function of C associated with observed image feature 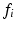 .
.
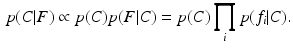
(1)
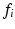 , as patches separated in scale and space do not typically exhibit direct correlations. On the RHS of Eq. (1), p(C) is a prior distribution over the clinical variable of interest C, and
, as patches separated in scale and space do not typically exhibit direct correlations. On the RHS of Eq. (1), p(C) is a prior distribution over the clinical variable of interest C, and 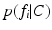 is the likelihood function of C associated with observed image feature
is the likelihood function of C associated with observed image feature 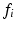 .
.We use a robust variant of kernel density estimation for calculating the class conditional likelihood densities:
![$$\begin{aligned} p(f_i|C) \propto \left[ \sum _{j:C_j=C} \frac{N}{N_C} \exp \left( -\frac{d^2(f_i,f_j)}{\alpha ^2+1}\right) \right] + \beta \frac{N_C}{N}. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_26_Chapter_Equ2.gif)
Here 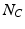 is the number of features of class C in the training data, and
is the number of features of class C in the training data, and 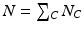 is the total feature count.
is the total feature count. 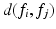 is the distance between
is the distance between 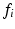 and neighboring descriptor
and neighboring descriptor 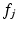 , here the Euclidean distance between descriptors.
, here the Euclidean distance between descriptors. 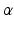 is an adaptive kernel bandwidth parameter that is empirically set to
is an adaptive kernel bandwidth parameter that is empirically set to 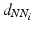 for each input feature
for each input feature 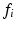 , i.e. the distance between
, i.e. the distance between 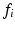 and the nearest neighboring descriptor
and the nearest neighboring descriptor 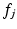 in a data base of training data:
in a data base of training data:
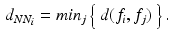
Finally, 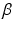 is a weighting parameter empirically set to
is a weighting parameter empirically set to 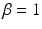 in experiments for best performance. Note that the overall scale of the likelihood is unimportant, as normalization can be performed after the product in Eq. (1) is computed.
in experiments for best performance. Note that the overall scale of the likelihood is unimportant, as normalization can be performed after the product in Eq. (1) is computed.
![$$\begin{aligned} p(f_i|C) \propto \left[ \sum _{j:C_j=C} \frac{N}{N_C} \exp \left( -\frac{d^2(f_i,f_j)}{\alpha ^2+1}\right) \right] + \beta \frac{N_C}{N}. \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_26_Chapter_Equ2.gif)
(2)
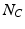 is the number of features of class C in the training data, and
is the number of features of class C in the training data, and 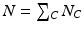 is the total feature count.
is the total feature count. 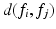 is the distance between
is the distance between 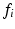 and neighboring descriptor
and neighboring descriptor 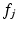 , here the Euclidean distance between descriptors.
, here the Euclidean distance between descriptors. 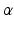 is an adaptive kernel bandwidth parameter that is empirically set to
is an adaptive kernel bandwidth parameter that is empirically set to 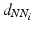 for each input feature
for each input feature 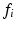 , i.e. the distance between
, i.e. the distance between 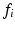 and the nearest neighboring descriptor
and the nearest neighboring descriptor 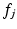 in a data base of training data:
in a data base of training data: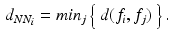
(3)
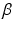 is a weighting parameter empirically set to
is a weighting parameter empirically set to 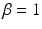 in experiments for best performance. Note that the overall scale of the likelihood is unimportant, as normalization can be performed after the product in Eq. (1) is computed.
in experiments for best performance. Note that the overall scale of the likelihood is unimportant, as normalization can be performed after the product in Eq. (1) is computed.In practice, Eq. 2 is computed for each 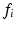 from a set of
from a set of 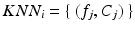 of K feature/label pairs
of K feature/label pairs 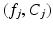 identified via an efficient approximate KNN search over a set of training feature data. Because the adaptive exponential kernel falls off quickly, it is not crucial to determine an optimal K as in some KNN methods [18], but rather to set K large enough include all features contributing to the kernel sum. Inuitively, the two terms in Eq. 2 are designed as a mixture model that is aimed at increasing the robustness of estimates when some of the features are “uninformative”. The first term is a density estimator that accounts for informative features in the data. It is a variant that combines aspects of kernel density estimation and KNN density estimation, using a kernel where the bandwidth is scaled by the distance to the first nearest neighbor as in Breiman et al. [20]. The second term
identified via an efficient approximate KNN search over a set of training feature data. Because the adaptive exponential kernel falls off quickly, it is not crucial to determine an optimal K as in some KNN methods [18], but rather to set K large enough include all features contributing to the kernel sum. Inuitively, the two terms in Eq. 2 are designed as a mixture model that is aimed at increasing the robustness of estimates when some of the features are “uninformative”. The first term is a density estimator that accounts for informative features in the data. It is a variant that combines aspects of kernel density estimation and KNN density estimation, using a kernel where the bandwidth is scaled by the distance to the first nearest neighbor as in Breiman et al. [20]. The second term 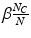 provides a default estimate for the case of uninformative features, curiously this class-specific value results in noticeably superior classification performance than a value that is uniform across classes.
provides a default estimate for the case of uninformative features, curiously this class-specific value results in noticeably superior classification performance than a value that is uniform across classes.
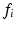 from a set of
from a set of 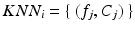 of K feature/label pairs
of K feature/label pairs 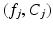 identified via an efficient approximate KNN search over a set of training feature data. Because the adaptive exponential kernel falls off quickly, it is not crucial to determine an optimal K as in some KNN methods [18], but rather to set K large enough include all features contributing to the kernel sum. Inuitively, the two terms in Eq. 2 are designed as a mixture model that is aimed at increasing the robustness of estimates when some of the features are “uninformative”. The first term is a density estimator that accounts for informative features in the data. It is a variant that combines aspects of kernel density estimation and KNN density estimation, using a kernel where the bandwidth is scaled by the distance to the first nearest neighbor as in Breiman et al. [20]. The second term
identified via an efficient approximate KNN search over a set of training feature data. Because the adaptive exponential kernel falls off quickly, it is not crucial to determine an optimal K as in some KNN methods [18], but rather to set K large enough include all features contributing to the kernel sum. Inuitively, the two terms in Eq. 2 are designed as a mixture model that is aimed at increasing the robustness of estimates when some of the features are “uninformative”. The first term is a density estimator that accounts for informative features in the data. It is a variant that combines aspects of kernel density estimation and KNN density estimation, using a kernel where the bandwidth is scaled by the distance to the first nearest neighbor as in Breiman et al. [20]. The second term 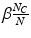 provides a default estimate for the case of uninformative features, curiously this class-specific value results in noticeably superior classification performance than a value that is uniform across classes.
provides a default estimate for the case of uninformative features, curiously this class-specific value results in noticeably superior classification performance than a value that is uniform across classes.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree