, Foster D. Lasley2, Indra J. Das2, Marc S. Mendonca2 and Joseph R. Dynlacht2
(1)
Department of Radiation Oncology, CHRISTUS St. Patrick Regional Cancer Center, Lake Charles, LA, USA
(2)
Department of Radiation Oncology, Indiana University School of Medicine, Indianapolis, IN, USA
Fractionation Definitions
Standard Fractionation: Once daily, 5 days/week, no more than 2 Gy/fraction.
Split Course: RT with planned treatment breaks.
Altered Fractionation: Anything other than standard fractionation.
Accelerated Fractionation: Any fractionation schedule that gives >10 Gy/week. Subtypes include:
Pure accelerated fractionation (2 Gy/fx, 6–7 fx/week)
Accelerated hypofractionation (>3 Gy/fx)
Accelerated hyperfractionation (>1 fx/day)
Hypofractionation: Increased fraction size, with or without decreased number of fractions/week.
Stereotactic Radiation (SRS/SBRT/SABR): RT delivered with stereotactic localization techniques in five fractions or less.
Fractionated Stereotactic RT (FSRT): RT delivered with stereotactic techniques and more than five fractions.
Hyperfractionation: Decreased fraction size with more than one fraction per day (BID or TID).
Concomitant Boost (CB): Two fractions per day with one fraction to a large field and the other to a boost volume.
Simultaneous Integrated Boost (SIB): One fraction per day with a higher dose to a boost volume and a lower dose to the large field.
The “4 R’s” of Radiobiology
Fractionated RT is biologically superior to single-fraction RT in most situations, and the “Four R’s” describe the biological effects of fractionation:
Repair (sublethal and potentially lethal damage repair)
Reoxygenation (acute and chronic hypoxia)
Redistribution (cell cycle and dose rate effects)
Repopulation
Repair is discussed in this chapter.
Repair increases cell survival after fractionated radiation, both for tumors and normal tissues.
Oxygen Effect and Reoxygenation are discussed in Chapts. 22 and 23.
Reoxygenation can increase tumor cell killing in previously hypoxic areas of tumors, but does not affect well oxygenated normal tissues.
Redistribution and Repopulation are discussed in Chapt. 24.
Redistribution can increase tumor cell killing as they enter more radiosensitive parts of the cell cycle.
Repopulation increases tumor and normal cell survival over the course of a prolonged treatment time.
The so-called “fifth R” is Radiosensitivity, which varies between different tissues and tumors.
Sublethal and Potentially Lethal Damage Repair
There are two different types of repairable damage that are measured by different assays.
SLDR and PLDR both contribute to the survival of cells, tissues, or tumors after irradiation.
Sublethal Damage Repair (SLDR)
Definition of SLD: DNA damage that is never lethal by itself but can become lethal if combined with additional damage.
See “Accumulated Intertrack Damage” (Chapt. 19).
Two radiation doses must be given. Cells are given time to repair between the two doses.
After the second dose, cells are immediately plated out to measure survival.
Mnemonic: SLD = Split Dose experiment.
Potentially Lethal Damage Repair (PLDR)
Definition of PLD: DNA damage that is lethal during cell division but can be repaired prior to cell division.
A single radiation dose is given.
After irradiation, cells are given time to repair under non-growth conditions, prior to plating out and measuring survival.
Mnemonic: PLD = Plating Delay experiment (Fig. 21.1).
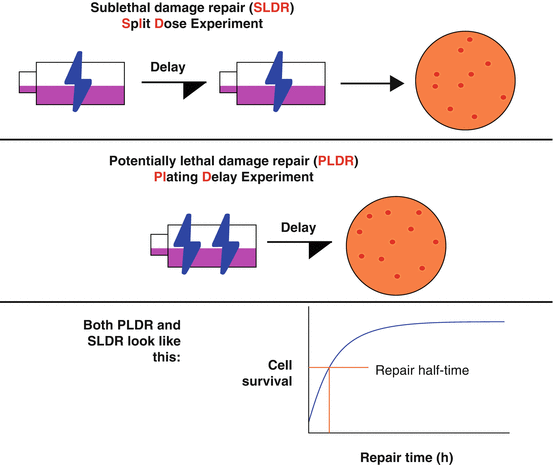
Fig. 21.1
Sub-lethal and potentially lethal damage are two different types of repairable damage. These are measured by a “Split Dose” and a “Plating Delay” experiment, respectively.
Half-Time of Repair
Repair occurs fairly rapidly, with a repair half-time of ~1 h in cell culture.
Repair times may be longer for late-responding normal tissue.
Repair is essentially complete by 6 h post-radiation.
Most twice-daily radiotherapy regimens use a minimum of 6 h between fractions.
Three times daily regimens may “cheat” with a 4 h minimum, mostly for scheduling reasons.
A Note on Mathematical Modeling
This chapter focuses on survival models for irradiation: single hit multitarget, two component, linear-quadratic, and models of biologically effective or equivalent dose.
All of these mathematical models are different ways to interpret the available data (cell survival, tumor control).
The linear-quadratic (α/β) model is most commonly used in the clinic due to its simplicity.
Far more sophisticated models exist in the literature.
Poisson Statistics: What Are They?
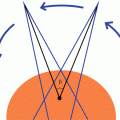
Poisson statistics describe a large number of random events happening to a large number of subjects, averaging out to a small number of events per subject (Fig. 21.2).

Fig. 21.2
Poisson statistics. This class of statistics may be described by the “raindrop analogy” as shown above. This is relevant to radiotherapy as radiation hitting cells is rather similar to raindrops hitting a board.
This is a pretty good approximation of radiation hitting cells.
At an average of X events per subject:
(e−X) subjects have no events.
(1 − e−X) subjects have at least one event.
Poisson Statistics and Cell Survival
The Poisson model is used for surviving fraction (SF) of cells:
At an average of X lethal hits per cell:
(e−X) cells survive. (No hits)
(1 − e−X) cells die. (at least 1 hit)
Based on this equation,
@ 1 hit per cell: SF = 0.37 (i.e. D 37 or D 0 )
@ 2 hits per cell: SF = 0.14
@ 2.3 hits per cell: SF = 0.10
@ 3 hits per cell: SF = 0.05
D 0 is defined as the radiation dose resulting in 37 % survival. This is assumed to be equal to the radiation dose necessary to cause one lethal hit per cell.
Poisson is also used for tumor control probability (TCP):
At an average of X surviving tumor cells per patient:
(e−X) patients are cured (no tumor cells).
(1 − e−X) patients recur. (at least 1 tumor cell).
Based on this equation,
@ 1 tumor cell per pt: TCP = 0.37
@ 0.5 tumor cells per pt: TCP = 0.61
@ 0.1 tumor cells per pt: TCP = 0.90
@ 0.05 tumor cells per pt: TCP = 0.95
@ 0.01 tumor cells per pt: TCP = 0.99
Rule of Thumb: To achieve a certain TCP, you should aim for a tumor cell survival of (1 − TCP).
Single-Hit, Multi-Target Model
This model assumes that each cell has multiple independent targets, all of which must be hit to produce cell killing.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree