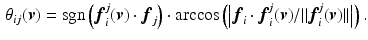Frames for Heart Fiber Reconstruction

m in diameter and 50–100 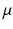$\mu$ m in length. Their primary function is to produce mechanical tension during ejection, but certain specialized cells also serve to conduct electrical activation of the heart muscle. Cardiomyocytes are densely and smoothly packed within a three-dimensional extracellular matrix principally made of connective tissue. The term myofiber is often used as a proxy for localized parallel groups of cardiomyocytes, although they do not exist at a microscopic level. Histological and medical imaging studies have established certain key geometrical properties of cardiac myofibers: (1) they form a smoothly varying medium which wraps around each ventricle, (2) this wrapping generates the truncated ellipsoidal shape of the myocardium, (3) focusing on the LV, the helix angle, which is the angle of cardiomyocyte orientation taken with respect to the short-axis plane smoothly rotates from outer to inner wall by a total amount of approximately 120 degrees.

3 Moving Frames in $\mathbf {R}^3$

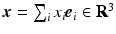Let a point ${\varvec{x}}=\sum _i x_i{\varvec{e}}_{i}\in \mathbf {R}^3$ be expressed in terms of 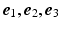${\varvec{e}}_{1}, {\varvec{e}}_{2}, {\varvec{e}}_{3}$ , the natural basis for 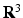$\mathbf {R}^3$ . We define a right-handed orthonormal frame field 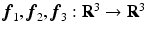${\varvec{f}}_{1}, {\varvec{f}}_{2}, {\varvec{f}}_{3}:\mathbf {R}^3\rightarrow \mathbf {R}^3$ . Each frame axis can be expressed by the rigid rotation 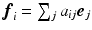${\varvec{f}}_{i} = \sum _j a_{ij}{\varvec{e}}_{j}$ , where 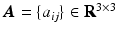$\varvec{A}=\{a_{ij}\}\in \mathbf {R}^{3\times 3}$ is a differentiable attitude matrix such that 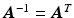$\varvec{A}^{-1}=\varvec{A}^T$ . 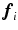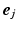Treating ${\varvec{f}}_{i}$ and ${\varvec{e}}_{j}$ as symbols, we can write [6]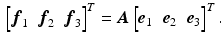

$\begin{aligned} \begin{bmatrix}{\varvec{f}}_{1}&{\varvec{f}}_{2}&{\varvec{f}}_{3} \end{bmatrix}^T = \varvec{A} \begin{bmatrix}{\varvec{e}}_{1}&{\varvec{e}}_{2}&{\varvec{e}}_{3} \end{bmatrix}^T. \end{aligned}$

(1)

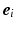Since each ${\varvec{e}}_{i}$ is constant, the differential geometry of the frame field is completely characterized by 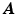$\varvec{A}$ . Taking the exterior derivative on both sides, we have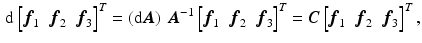

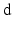$\begin{aligned} \text {d}\begin{bmatrix}{\varvec{f}}_{1}&{\varvec{f}}_{2}&{\varvec{f}}_{3} \end{bmatrix}^T =\left( \text {d}\varvec{A}\right) \,\varvec{A}^{-1} \begin{bmatrix}{\varvec{f}}_{1}&{\varvec{f}}_{2}&{\varvec{f}}_{3} \end{bmatrix}^T = \varvec{C} \begin{bmatrix}{\varvec{f}}_{1}&{\varvec{f}}_{2}&{\varvec{f}}_{3} \end{bmatrix}^T, \end{aligned}$

(2)

where $\text {d}$ denotes the exterior derivative, and 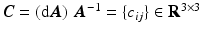$\varvec{C}=\left( \text {d}\varvec{A}\right) \,\varvec{A}^{-1}=\{c_{ij}\}\in \mathbf {R}^{3\times 3}$ is the Maurer-Cartan matrix of connection forms 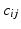$c_{ij}$ . Writing 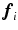${\varvec{f}}_{i}$ as symbols, (2) is to be understood as 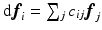$\text {d}{\varvec{f}}_{i} = \sum _j c_{ij}{\varvec{f}}_{j}$ . The Maurer-Cartan matrix is skew symmetric [6], hence we have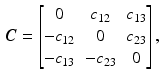

$\begin{aligned} \varvec{C} = \begin{bmatrix}0&c_{12}&c_{13} \\ - c_{12}&0&c_{23} \\ - c_{13}&-c_{23}&0 \end{bmatrix}, \end{aligned}$

(3)

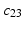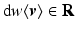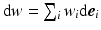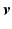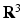such that there are at most 3 independent, non-zero 1-forms: $c_{12}$ , $c_{13}$ , and $c_{23}$ . 1-forms operate on tangent vectors through a process denoted contraction, written as $\text {d}w\langle {\varvec{v}}\rangle \in \mathbf {R}$ for a general 1-form $\text {d}w=\sum _iw_i\text {d}{\varvec{e}}_{i}$ and tangent vector ${\varvec{v}}$ on $\mathbf {R}^3$ , which yields 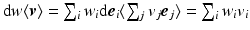$\text {d}w\langle {\varvec{v}}\rangle = \sum _i w_i\text {d}{\varvec{e}}_{i}\langle \sum _j v_j{\varvec{e}}_{j}\rangle = \sum _i w_iv_i$ , since 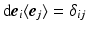$\text {d}{\varvec{e}}_{i}\langle {\varvec{e}}_{j}\rangle =\delta _{ij}$ , where 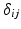$\delta _{ij}$ is the Kronecker delta.

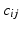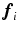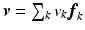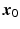The space of linear models for smooth frame fields is fully parametrized by the 1-forms $c_{ij}$ . This space can be explored by considering the motion of ${\varvec{f}}_{i}$ in a direction ${\varvec{v}}=\sum _k v_k {\varvec{f}}_{k}$ , using the first order terms of a Taylor series centered at ${\varvec{x}}_0$ :

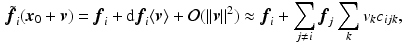
$\begin{aligned} \tilde{{\varvec{f}}_{i}}({\varvec{x}}_0+{\varvec{v}})&= {\varvec{f}}_{i} + \text {d}{\varvec{f}}_{i}\langle {\varvec{v}}\rangle +\mathcal {O}(\left| \left| {{\varvec{v}}}\right| \right| ^2)\approx {\varvec{f}}_{i}+\sum _{j\ne i} {\varvec{f}}_{j}\sum _k v_kc_{ijk}, \end{aligned}$

(4)

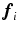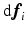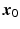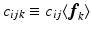where ${\varvec{f}}_{i}$ and $\text {d}{\varvec{f}}_{i}$ are evaluated at ${\varvec{x}}_0$ , and $c_{ijk}\equiv c_{ij}\langle {\varvec{f}}_{k}\rangle$ are the connection forms of the local frame. Since only 3 unique non-zero combinations of 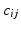$c_{ij}$ are possible, there are in total 9 connections 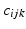$c_{ijk}$ . 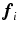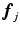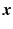These coefficients express the rate of turn of the frame vector ${\varvec{f}}_{i}$ towards ${\varvec{f}}_{j}$ when ${\varvec{x}}$ moves in the direction 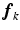${\varvec{f}}_{k}$ . Figure 1 illustrates the behavior of the frame field described by 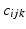$c_{ijk}$ . For example, with 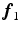${\varvec{f}}_{1}$ taken to be the local orientation of a fiber and 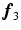${\varvec{f}}_{3}$ taken to be the component of the heart wall normal orthogonal to 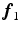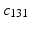${\varvec{f}}_{1}$ , $c_{131}$ measures the circumferential curvature of a fiber and 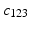$c_{123}$ measures the change in its helix angle [9].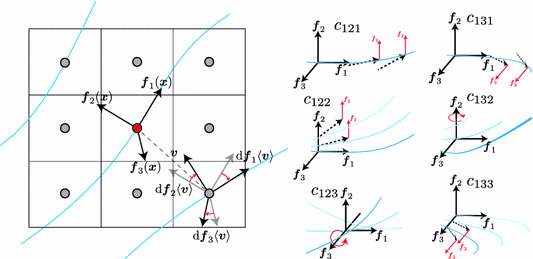

Fig. 1.

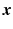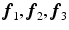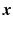(Left) Turning of frame axes at ${\varvec{x}}$ expressed in the local basis ${\varvec{f}}_{1},{\varvec{f}}_{2},{\varvec{f}}_{3}$ when ${\varvec{x}}$ moves in the direction 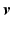${\varvec{v}}$ . (Right) frame field variation characterized by the connections 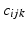$c_{ijk}$ for $$i=1$$

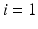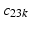( $c_{23k}$ are not shown).

4 Computation of Connection Forms

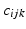A first order generator for frame fields using (4) requires knowledge of the underlying connection forms $c_{ijk}$ . We shall explore three ways of computing these: (1) a direct estimate based on finite differences, (2) a regularized optimization scheme, and (3) a novel closed-form computation which yields exact results on linear manifolds. In Sect. 4.4 we discuss conditions under which each method could be used, and later in Sect. 5 we use various combinations of these for inpainting 3D frame fields.

4.1 Connections via Finite Differentiation

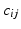In smooth frame fields, the connection 1-forms $c_{ij}$ can be directly obtained using (2), i.e., 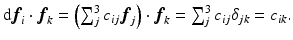$\text {d}{\varvec{f}}_{i}\cdot {\varvec{f}}_{k}=\left( \sum _j^3c_{ij}{\varvec{f}}_{j}\right) \cdot {\varvec{f}}_{k}=\sum _j^3c_{ij}\delta _{jk}=c_{ik}.$ The differentials 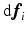$\text {d}{\varvec{f}}_{i}$ can be computed by applying the exterior derivative for a function, i.e., for the k’th component of ${\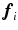varvec{f}}_{i}$ , ${\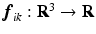varvec{f}}_{ik}:\mathbf {R}^3\rightarrow \mathbf {R}$ , $\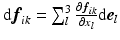text {d}{\varvec{f}}_{ik}=\sum _l^3\frac{\partial {\varvec{f}}_{ik}}{\partial x_l}\text {d}{\varvec{e}}_{l}$ ,

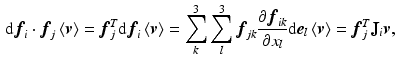
$\begin{aligned} \text {d}{\varvec{f}}_{i}\cdot {\varvec{f}}_{j}\left\langle {\varvec{v}}\right\rangle ={\varvec{f}}_{j}^T\text {d}{\varvec{f}}_{i}\left\langle {\varvec{v}}\right\rangle&=\sum _k^3\sum _l^3 {\varvec{f}}_{jk}\frac{\partial {\varvec{f}}_{ik}}{\partial x_l}\text {d}{\varvec{e}}_{l}\left\langle {\varvec{v}}\right\rangle ={\varvec{f}}_{j}^T\mathbf {J}_i{\varvec{v}}, \end{aligned}$

(5)

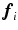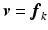where $\mathbf {J}_i=\left[ \frac{\partial {\varvec{f}}_{ip}}{\partial x_q}\right] \in \mathbf {R}^{3\times 3}$ is the Jacobian matrix of partial derivatives of ${\varvec{f}}_{i}$ . Setting ${\varvec{v}}={\varvec{f}}_{k}$ , we obtain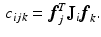

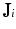$\begin{aligned} c_{ijk}={\varvec{f}}_{j}^T\mathbf {J}_i{\varvec{f}}_{k}. \end{aligned}$

(6)

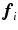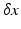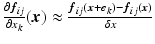The Jacobian matrix $\mathbf {J}_i$ can be approximated to first order using, e.g., finite differences on ${\varvec{f}}_{i}$ with a spacing of size $\delta x$ : $\frac{\partial {\varvec{f}}_{ij}}{\partial x_k}({\varvec{x}})\approx \frac{{\varvec{f}}_{ij}({\varvec{x}}+{\varvec{e}}_{k})-{\varvec{f}}_{ij}({\varvec{x}})}{\delta x}$ .

4.2 Connections via Energy Minimization

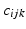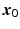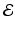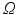The connection forms $c_{ijk}$ at a point ${\varvec{x}}_0$ can also be obtained as the minimizer of an extrapolation energy $\mathcal E$ contained within a neighborhood $\varOmega$ :

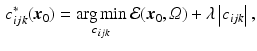
$\begin{aligned} c_{ijk}^*({\varvec{x}}_0)=\mathop {\arg \min }\limits _{c_{ijk}} \mathcal E({\varvec{x}}_0, \varOmega )+\lambda \left| c_{ijk}\right| , \end{aligned}$

(7)

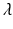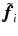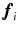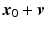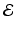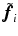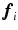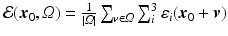where $\lambda$ is a regularization weight used to penalize high curvature. Denoting $\tilde{{\varvec{f}}_{i}}$ as the normalized approximation to ${\varvec{f}}_{i}$ at ${\varvec{x}}_0+{\varvec{v}}$ using (4), we follow [8] and choose $\mathcal E$ to minimize the angular error between $\tilde{{\varvec{f}}_{i}}$ and ${\varvec{f}}_{i}$ : $\mathcal E({\varvec{x}}_0, \varOmega )= \frac{1}{|\varOmega |}\sum _{{\varvec{v}}\in \varOmega }\sum _i^3 \varepsilon _i({\varvec{x}}_0+{\varvec{v}})$ , with $\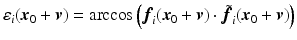varepsilon _i({\varvec{x}}_0+{\varvec{v}}) = \arccos \left( {\varvec{f}}_{i} ({\varvec{x}}_0+{\varvec{v}})\cdot \tilde{{\varvec{f}}_{i}}({\varvec{x}}_0+{\varvec{v}})\right)$ .

4.3 Closed-Form Connections in Linear Space

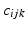A disadvantage of using the previous energy minimization approach is that coupling between the connections $c_{ijk}$ is not explicitly enforced, i.e., the requirement that 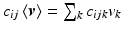$c_{ij}\left\langle {\varvec{v}}\right\rangle =\sum _k c_{ijk}v_k$ . Thus it may lead to non-integrable differential descriptors. We now develop a novel way of computing connection forms that is based on trigonometrical considerations in the first-order structure of 3D frame fields and which enforces that coupling. This method also provides exact 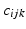$c_{ijk}$ measurements in manifolds that have low second-order curvatures ( 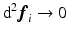$\text {d}^2 {\varvec{f}}_{i}\rightarrow 0$ ). Given a local basis 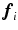${\varvec{f}}_{i}$ and data-driven neighboring bases 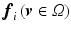${\varvec{f}}_{i}\left( {\varvec{v}}\in \varOmega \right)$ , the 1-forms 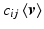$c_{ij}\left\langle {\varvec{v}}\right\rangle$ can be solved for using linear least-squares. We begin by expanding (4),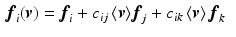

$\begin{aligned} {\varvec{f}}_{i}({\varvec{v}}) = {\varvec{f}}_{i}+c_{ij}\left\langle {\varvec{v}}\right\rangle&{\varvec{f}}_{j}+c_{ik}\left\langle {\varvec{v}}\right\rangle {\varvec{f}}_{k} \end{aligned}$

(8)

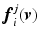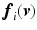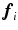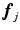and analyze this expression geometrically using Fig. 2. Let ${\varvec{f}}_{i}^{j}({\varvec{v}})$ denote the projection of ${\varvec{f}}_{i}({\varvec{v}})$ in the ${\varvec{f}}_{i}$ – ${\varvec{f}}_{j}$ plane, i.e., 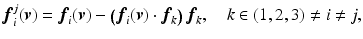${\varvec{f}}_{i}^{j}({\varvec{v}}) = {\varvec{f}}_{i}({\varvec{v}}) - \left( {\varvec{f}}_{i}({\varvec{v}})\cdot {\varvec{f}}_{k}\right) {\varvec{f}}_{k}, \quad k\in \left( 1,2,3\right) \ne i\ne j,$ and let 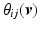$\theta _{ij}({\varvec{v}})$ denote the signed angle between 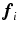${\varvec{f}}_{i}$ and ${\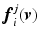varvec{f}}_{i}^j({\varvec{v}})$ with positive values assigned to 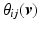$\theta _{ij}({\varvec{v}})$ rotating 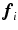${\varvec{f}}_{i}$ towards 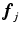${\varvec{f}}_{j}$ , obtained as

$\begin{aligned} \theta _{ij}({\varvec{v}})=\text {sgn}\left( {\varvec{f}}_{i}^j({\varvec{v}})\cdot {\varvec{f}}_{j}\right) \cdot \arccos \left( \left| {\varvec{f}}_{i}\cdot {\varvec{f}}_{i}^j({\varvec{v}})/||{\varvec{f}}_{i}^j({\varvec{v}})||\right| \right) . \end{aligned}$