for n points. Since this algorithm has the same complexity as the spectral analysis, it cannot be directly used as a subset selection scheme.
In this paper, we focus on nonlinear dimensionality reduction for large datasets via manifold learning. Popular manifold learning techniques include kernel PCA, Isomap [19], and Laplacian eigenmaps [5]. All of these methods are based on a kernel matrix of size 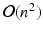 that contains the information about the pairwise relationships between the input points. The spectral decomposition of the kernel matrix leads to the low-dimensional embedding of the points. For large n, one seeks to avoid the explicit construction and storage of the matrix. In contrast to general rank-k matrix approximation, this is possible by taking the nature of the non-linear dimensionality reduction into account and relating the entries of the kernel matrix directly to the original point set.
that contains the information about the pairwise relationships between the input points. The spectral decomposition of the kernel matrix leads to the low-dimensional embedding of the points. For large n, one seeks to avoid the explicit construction and storage of the matrix. In contrast to general rank-k matrix approximation, this is possible by taking the nature of the non-linear dimensionality reduction into account and relating the entries of the kernel matrix directly to the original point set.
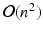 that contains the information about the pairwise relationships between the input points. The spectral decomposition of the kernel matrix leads to the low-dimensional embedding of the points. For large n, one seeks to avoid the explicit construction and storage of the matrix. In contrast to general rank-k matrix approximation, this is possible by taking the nature of the non-linear dimensionality reduction into account and relating the entries of the kernel matrix directly to the original point set.
that contains the information about the pairwise relationships between the input points. The spectral decomposition of the kernel matrix leads to the low-dimensional embedding of the points. For large n, one seeks to avoid the explicit construction and storage of the matrix. In contrast to general rank-k matrix approximation, this is possible by taking the nature of the non-linear dimensionality reduction into account and relating the entries of the kernel matrix directly to the original point set.We propose to perform DPP sampling on the original point set to extract a diverse set of landmarks. Since the input points lie in a non-Euclidean space, ignoring the underlying geometry leads to poor results. To account for the non-Euclidean geometry of the input space, we replace the Euclidean distance with the geodesic distance along the manifold, which is approximated by the shortest path distance on the graph. Due to the high complexity of DPP sampling, we derive an efficient approximation that runs in 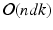 with input dimensionality d and subset cardinality k. The algorithm restricts the updates to be local, which enables sampling on complex geometries. This, together with its low computational complexity, makes the algorithm well suited for the subset selection in large scale manifold learning.
with input dimensionality d and subset cardinality k. The algorithm restricts the updates to be local, which enables sampling on complex geometries. This, together with its low computational complexity, makes the algorithm well suited for the subset selection in large scale manifold learning.
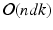 with input dimensionality d and subset cardinality k. The algorithm restricts the updates to be local, which enables sampling on complex geometries. This, together with its low computational complexity, makes the algorithm well suited for the subset selection in large scale manifold learning.
with input dimensionality d and subset cardinality k. The algorithm restricts the updates to be local, which enables sampling on complex geometries. This, together with its low computational complexity, makes the algorithm well suited for the subset selection in large scale manifold learning.A consequence of the landmark selection is that the manifold is less densely sampled than before, making its approximation with neighborhood graphs more difficult. It was noted in [2], as a critical response to [19], that the approximation of manifolds with graphs is topologically unstable. In order to improve the graph construction, we retain the local geometry around each landmark by locally estimating the covariance matrix on the original point set. This allows us to compare multivariate Gaussian distributions with the Bhattacharyya distance for neighborhood selection, yielding improved embeddings.
2 Background
We assume n points in high dimensional space 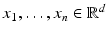 and let
and let 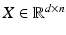 be the matrix whose i-th column represents point
be the matrix whose i-th column represents point 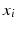 . Non-linear dimensionality reduction techniques are based on a positive semidefinite kernel K, with a typical choice of Gaussian or heat kernel
. Non-linear dimensionality reduction techniques are based on a positive semidefinite kernel K, with a typical choice of Gaussian or heat kernel 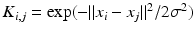 . The resulting kernel matrix is of size
. The resulting kernel matrix is of size 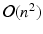 . The eigen decomposition of the kernel matrix is necessary for spectral analysis. Unfortunately, its complexity is
. The eigen decomposition of the kernel matrix is necessary for spectral analysis. Unfortunately, its complexity is 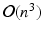 . Most techniques require only the top k eigenvectors. The problem can therefore also be viewed as finding the best rank-k approximation of the matrix K, with the optimal solution
. Most techniques require only the top k eigenvectors. The problem can therefore also be viewed as finding the best rank-k approximation of the matrix K, with the optimal solution 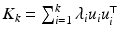 , where
, where 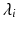 is the i-th largest eigenvalue and
is the i-th largest eigenvalue and 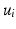 is the corresponding eigenvector.
is the corresponding eigenvector.
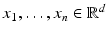 and let
and let 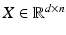 be the matrix whose i-th column represents point
be the matrix whose i-th column represents point 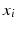 . Non-linear dimensionality reduction techniques are based on a positive semidefinite kernel K, with a typical choice of Gaussian or heat kernel
. Non-linear dimensionality reduction techniques are based on a positive semidefinite kernel K, with a typical choice of Gaussian or heat kernel 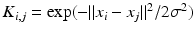 . The resulting kernel matrix is of size
. The resulting kernel matrix is of size 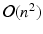 . The eigen decomposition of the kernel matrix is necessary for spectral analysis. Unfortunately, its complexity is
. The eigen decomposition of the kernel matrix is necessary for spectral analysis. Unfortunately, its complexity is 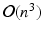 . Most techniques require only the top k eigenvectors. The problem can therefore also be viewed as finding the best rank-k approximation of the matrix K, with the optimal solution
. Most techniques require only the top k eigenvectors. The problem can therefore also be viewed as finding the best rank-k approximation of the matrix K, with the optimal solution 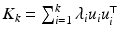 , where
, where 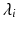 is the i-th largest eigenvalue and
is the i-th largest eigenvalue and 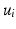 is the corresponding eigenvector.
is the corresponding eigenvector.2.1 Nyström Method
Suppose 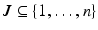 is a subset of the original point set of size k and
is a subset of the original point set of size k and 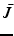 is its complement. We can reorder the kernel matrix K such that
is its complement. We can reorder the kernel matrix K such that
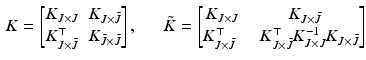
where 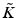 is the matrix estimated via the Nyström method [21]. The Nyström extension leads to the approximation
is the matrix estimated via the Nyström method [21]. The Nyström extension leads to the approximation 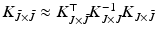 . The matrix inverse is replaced by the Moore-Penrose generalized inverse in the case of rank deficiency. The Nyström method leads to the minimal kernel completion [3] conditioned on the selected landmarks and has been reported to perform well in numerous applications [8, 13, 18]. The challenge lies in finding landmarks that minimize the reconstruction error
. The matrix inverse is replaced by the Moore-Penrose generalized inverse in the case of rank deficiency. The Nyström method leads to the minimal kernel completion [3] conditioned on the selected landmarks and has been reported to perform well in numerous applications [8, 13, 18]. The challenge lies in finding landmarks that minimize the reconstruction error
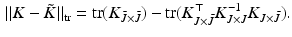
The trace norm 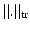 is applied because results only depend on the spectrum due to its unitary invariance.
is applied because results only depend on the spectrum due to its unitary invariance.
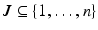 is a subset of the original point set of size k and
is a subset of the original point set of size k and 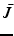 is its complement. We can reorder the kernel matrix K such that
is its complement. We can reorder the kernel matrix K such that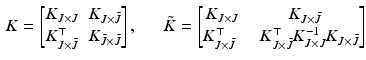
(1)
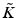 is the matrix estimated via the Nyström method [21]. The Nyström extension leads to the approximation
is the matrix estimated via the Nyström method [21]. The Nyström extension leads to the approximation 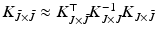 . The matrix inverse is replaced by the Moore-Penrose generalized inverse in the case of rank deficiency. The Nyström method leads to the minimal kernel completion [3] conditioned on the selected landmarks and has been reported to perform well in numerous applications [8, 13, 18]. The challenge lies in finding landmarks that minimize the reconstruction error
. The matrix inverse is replaced by the Moore-Penrose generalized inverse in the case of rank deficiency. The Nyström method leads to the minimal kernel completion [3] conditioned on the selected landmarks and has been reported to perform well in numerous applications [8, 13, 18]. The challenge lies in finding landmarks that minimize the reconstruction error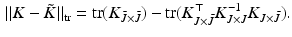
(2)
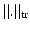 is applied because results only depend on the spectrum due to its unitary invariance.
is applied because results only depend on the spectrum due to its unitary invariance.2.2 Annealed Determinantal Sampling
A large variety of methods have been proposed for selecting the subset J. For general matrix approximation, this step is referred to as row/column selection of the matrix K, which is equivalent to selecting a subset of points X. This property is important because it avoids explicit computation of the 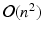 entries in the kernel matrix K. We focus on volume sampling for subset selection because of its theoretical advantages [9]. We employ the factorization
entries in the kernel matrix K. We focus on volume sampling for subset selection because of its theoretical advantages [9]. We employ the factorization 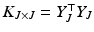 , which exists because
, which exists because 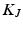 is positive semidefinite. Columns in
is positive semidefinite. Columns in 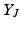 can be thought of as feature vectors describing the selected points. Based on this factorization, the volume
can be thought of as feature vectors describing the selected points. Based on this factorization, the volume 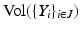 of the simplex spanned by the origin and the feature vectors
of the simplex spanned by the origin and the feature vectors 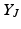 is calculated, which is equivalent to the volume of the parallelepiped spanned by
is calculated, which is equivalent to the volume of the parallelepiped spanned by 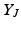 . The subset J is then sampled proportionally to the squared volume. This is directly related to the calculation of the determinant with
. The subset J is then sampled proportionally to the squared volume. This is directly related to the calculation of the determinant with 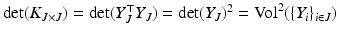 . These ideas were further generalized in [3] based on annealed determinantal distributions
. These ideas were further generalized in [3] based on annealed determinantal distributions
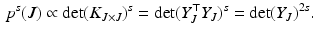
This distribution is well defined because the principal submatrices of a positive semidefinite matrix are themselves positive semidefinite. Varying the exponent 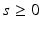 results in a family of distributions, modeling the annealing behavior as used in stochastic computations. For
results in a family of distributions, modeling the annealing behavior as used in stochastic computations. For 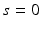 this is equivalent to uniform sampling [21]. In the following derivations, we focus on
this is equivalent to uniform sampling [21]. In the following derivations, we focus on 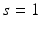 . It was shown in [9] that for
. It was shown in [9] that for 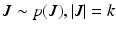
![$$\begin{aligned} {\mathbb E} \left[ \Vert K - \tilde{K}\Vert _{\text {tr}} \right] \le (k+1) \Vert K - K_k \Vert ^2_F, \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_54_Chapter_Equ4.gif)
where 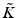 is the Nyström reconstruction of the kernel based on the subset J,
is the Nyström reconstruction of the kernel based on the subset J, 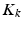 the best rank-k approximation achieved by selecting the largest eigenvectors, and
the best rank-k approximation achieved by selecting the largest eigenvectors, and 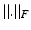 the Frobenius norm. It was further shown that the factor
the Frobenius norm. It was further shown that the factor 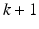 is the best possible for a k-subset. Related bounds were presented in [4].
is the best possible for a k-subset. Related bounds were presented in [4].
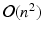 entries in the kernel matrix K. We focus on volume sampling for subset selection because of its theoretical advantages [9]. We employ the factorization
entries in the kernel matrix K. We focus on volume sampling for subset selection because of its theoretical advantages [9]. We employ the factorization 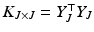 , which exists because
, which exists because 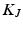 is positive semidefinite. Columns in
is positive semidefinite. Columns in 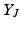 can be thought of as feature vectors describing the selected points. Based on this factorization, the volume
can be thought of as feature vectors describing the selected points. Based on this factorization, the volume 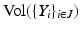 of the simplex spanned by the origin and the feature vectors
of the simplex spanned by the origin and the feature vectors 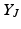 is calculated, which is equivalent to the volume of the parallelepiped spanned by
is calculated, which is equivalent to the volume of the parallelepiped spanned by 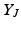 . The subset J is then sampled proportionally to the squared volume. This is directly related to the calculation of the determinant with
. The subset J is then sampled proportionally to the squared volume. This is directly related to the calculation of the determinant with 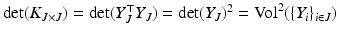 . These ideas were further generalized in [3] based on annealed determinantal distributions
. These ideas were further generalized in [3] based on annealed determinantal distributions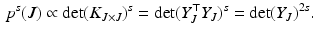
(3)
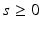 results in a family of distributions, modeling the annealing behavior as used in stochastic computations. For
results in a family of distributions, modeling the annealing behavior as used in stochastic computations. For 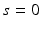 this is equivalent to uniform sampling [21]. In the following derivations, we focus on
this is equivalent to uniform sampling [21]. In the following derivations, we focus on 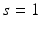 . It was shown in [9] that for
. It was shown in [9] that for 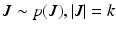
![$$\begin{aligned} {\mathbb E} \left[ \Vert K - \tilde{K}\Vert _{\text {tr}} \right] \le (k+1) \Vert K - K_k \Vert ^2_F, \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_54_Chapter_Equ4.gif)
(4)
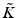 is the Nyström reconstruction of the kernel based on the subset J,
is the Nyström reconstruction of the kernel based on the subset J, 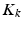 the best rank-k approximation achieved by selecting the largest eigenvectors, and
the best rank-k approximation achieved by selecting the largest eigenvectors, and 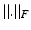 the Frobenius norm. It was further shown that the factor
the Frobenius norm. It was further shown that the factor 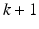 is the best possible for a k-subset. Related bounds were presented in [4].
is the best possible for a k-subset. Related bounds were presented in [4].
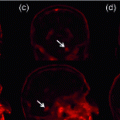
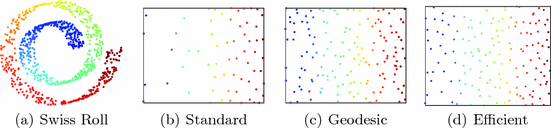
Fig. 1.
DPP sampling from 1,000 points lying on a manifold. We show results for standard DPP sampling, geodesic DPP sampling, and efficient DPP sampling. Note that the sampling is performed in 3D, but we can plot the underlying 2D manifold by reversing the construction of the Swiss roll. Geodesic and efficient sampling yields a diverse subset from the manifold.
3 Method
We first analyze the sampling from determinantal distributions on non-Euclidean geometries. We then introduce an efficient algorithm for approximate DPP sampling on manifolds. Finally, we present our approach for robust graph construction on sparsely sampled manifolds.
3.1 DPP Sampling on Manifolds
As described in Sect. 2.2, sampling from determinantal distributions is used for row/column selection. Independently, determinantal point processes (DPPs) were introduced for modeling probabilistic mutual exclusion. They present an attractive scheme for ensuring diversity in the selected subset. Here we work with the construction of DPPs based on L-ensembles [7]. Given a positive semidefinite matrix 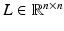 , the likelihood for selecting the subset
, the likelihood for selecting the subset 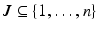 is
is
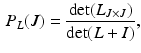
where I is the identity matrix and 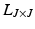 is the sub-matrix of L containing the rows and columns indexed by J. By associating the L-ensemble matrix L with the kernel matrix K, we can apply DPPs to sample subsets from the point set X.
is the sub-matrix of L containing the rows and columns indexed by J. By associating the L-ensemble matrix L with the kernel matrix K, we can apply DPPs to sample subsets from the point set X.
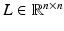 , the likelihood for selecting the subset
, the likelihood for selecting the subset 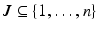 is
is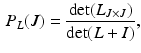
(5)
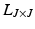 is the sub-matrix of L containing the rows and columns indexed by J. By associating the L-ensemble matrix L with the kernel matrix K, we can apply DPPs to sample subsets from the point set X.
is the sub-matrix of L containing the rows and columns indexed by J. By associating the L-ensemble matrix L with the kernel matrix K, we can apply DPPs to sample subsets from the point set X.To date, applications using determinantal point processes have assumed Euclidean geometry [15]. For non-linear dimensionality reduction, we assume that the data points lie in a non-Euclidean space, such as the Swiss roll in Fig. 1(a). To evaluate the performance of DPPs on manifolds, we sample from the Swiss roll. Since we know the construction rule in this case, we can invert it and display the sampled 3D points in the underlying 2D space. The result in Fig. 1(b) shows that the inner part of the roll is almost entirely neglected, as a consequence of not taking the manifold structure into account. A common solution is to use geodesic distances [19], which can be approximated by the graph shortest path algorithm. We replace the Euclidean distance 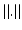 in the construction of the kernel matrix K with the geodesic distance
in the construction of the kernel matrix K with the geodesic distance 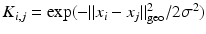 to obtain the result in Fig. 1(c). We observe a clear improvement in the diversity of the sampling, now also including points in the interior part of the Swiss roll.
to obtain the result in Fig. 1(c). We observe a clear improvement in the diversity of the sampling, now also including points in the interior part of the Swiss roll.
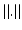 in the construction of the kernel matrix K with the geodesic distance
in the construction of the kernel matrix K with the geodesic distance 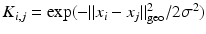 to obtain the result in Fig. 1(c). We observe a clear improvement in the diversity of the sampling, now also including points in the interior part of the Swiss roll.
to obtain the result in Fig. 1(c). We observe a clear improvement in the diversity of the sampling, now also including points in the interior part of the Swiss roll.3.2 Efficient Approximation of DPP Sampling on Manifolds
While it is possible to adapt determinantal sampling to non-Euclidean geometries and to characterize the error for the subset selection, we are missing an efficient sampling algorithm for handling large point sets. In [9], an approximative sampling based on the Markov chain Monte Carlo method is proposed to circumvent the combinatorial problem with 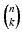 possible subsets. Further approximations include sampling proportionally to the diagonal elements
possible subsets. Further approximations include sampling proportionally to the diagonal elements 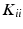 or their squared version
or their squared version 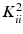 , leading to additive error bounds [4, 11]. In [10], an algorithm is proposed that yields a k! approximation to volume sampling, worsening the approximation from
, leading to additive error bounds [4, 11]. In [10], an algorithm is proposed that yields a k! approximation to volume sampling, worsening the approximation from 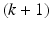 to
to 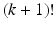 .
.

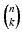 possible subsets. Further approximations include sampling proportionally to the diagonal elements
possible subsets. Further approximations include sampling proportionally to the diagonal elements 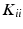 or their squared version
or their squared version 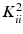 , leading to additive error bounds [4, 11]. In [10], an algorithm is proposed that yields a k! approximation to volume sampling, worsening the approximation from
, leading to additive error bounds [4, 11]. In [10], an algorithm is proposed that yields a k! approximation to volume sampling, worsening the approximation from 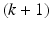 to
to 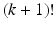 .
.
An exact sampling algorithm for DPPs was presented in [14, 15], which requires the eigen decomposition of 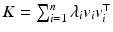 . Algorithm 1 states an equivalent formulation of this sampling approach. First, eigenvectors are selected proportionally to the magnitude of their eigenvalues and stored as columns in V. Assuming m vectors are selected,
. Algorithm 1 states an equivalent formulation of this sampling approach. First, eigenvectors are selected proportionally to the magnitude of their eigenvalues and stored as columns in V. Assuming m vectors are selected, 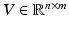 . By setting
. By setting 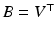 , we use
, we use 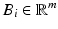 to denote the rows of V. In each iteration, we select one of the n points where point i is selected proportionally to the squared norm
to denote the rows of V. In each iteration, we select one of the n points where point i is selected proportionally to the squared norm 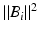 . The selected point is added to the subset J. After the selection of i, all vectors
. The selected point is added to the subset J. After the selection of i, all vectors 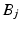 are projected to the orthogonal space of
are projected to the orthogonal space of 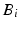 . Since
. Since 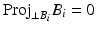 , the same point is almost surely not selected twice. The update formulation differs from [15], where an orthonormal basis of the eigenvectors in V perpendicular to the i-th basis vector
, the same point is almost surely not selected twice. The update formulation differs from [15], where an orthonormal basis of the eigenvectors in V perpendicular to the i-th basis vector 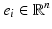 is constructed. Both formulations are equivalent but provide a different point of view on the algorithm. This modification is essential to motivate the proposed efficient sampling procedure. The following proposition characterizes the behavior of the update rule in the algorithm.
is constructed. Both formulations are equivalent but provide a different point of view on the algorithm. This modification is essential to motivate the proposed efficient sampling procedure. The following proposition characterizes the behavior of the update rule in the algorithm.
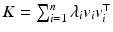 . Algorithm 1 states an equivalent formulation of this sampling approach. First, eigenvectors are selected proportionally to the magnitude of their eigenvalues and stored as columns in V. Assuming m vectors are selected,
. Algorithm 1 states an equivalent formulation of this sampling approach. First, eigenvectors are selected proportionally to the magnitude of their eigenvalues and stored as columns in V. Assuming m vectors are selected, 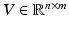 . By setting
. By setting 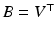 , we use
, we use 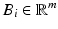 to denote the rows of V. In each iteration, we select one of the n points where point i is selected proportionally to the squared norm
to denote the rows of V. In each iteration, we select one of the n points where point i is selected proportionally to the squared norm 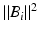 . The selected point is added to the subset J. After the selection of i, all vectors
. The selected point is added to the subset J. After the selection of i, all vectors 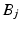 are projected to the orthogonal space of
are projected to the orthogonal space of 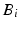 . Since
. Since 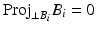 , the same point is almost surely not selected twice. The update formulation differs from [15], where an orthonormal basis of the eigenvectors in V perpendicular to the i-th basis vector
, the same point is almost surely not selected twice. The update formulation differs from [15], where an orthonormal basis of the eigenvectors in V perpendicular to the i-th basis vector 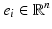 is constructed. Both formulations are equivalent but provide a different point of view on the algorithm. This modification is essential to motivate the proposed efficient sampling procedure. The following proposition characterizes the behavior of the update rule in the algorithm.
is constructed. Both formulations are equivalent but provide a different point of view on the algorithm. This modification is essential to motivate the proposed efficient sampling procedure. The following proposition characterizes the behavior of the update rule in the algorithm.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree