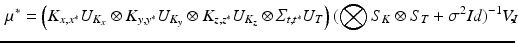be the 3-dimensional spatial coordinate system and t the temporal dimension. We consider the image time series I as a discretely sampled spatio-temporal signal of dimensions 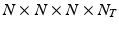 , where N is the dimension of the sampling grid on a single spatial axis, and
, where N is the dimension of the sampling grid on a single spatial axis, and 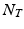 is the number of time points1. In the following sections we represent the image time-series I as a single dimensional array of dimensions
is the number of time points1. In the following sections we represent the image time-series I as a single dimensional array of dimensions 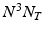 . We model the image time series I(u, t) as a realization of a latent spatio-temporal process f(u, t) with additive noise:
. We model the image time series I(u, t) as a realization of a latent spatio-temporal process f(u, t) with additive noise:
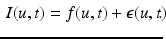
(1)
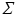 , while
, while 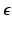 is assumed to be i.i.d. Gaussian distributed measurement noise
is assumed to be i.i.d. Gaussian distributed measurement noise 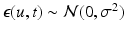 . Here we first assume that spatial and temporal processes are separable, and thus that the covariance matrix
. Here we first assume that spatial and temporal processes are separable, and thus that the covariance matrix 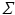 can be factorised in the Kronecker product of independent spatial and temporal covariance matrices:
can be factorised in the Kronecker product of independent spatial and temporal covariance matrices: 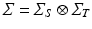 .
.This is a valid modeling assumption when the temporal properties of the signal are similar across space; for instance, when analyzing within-subject time series of brain MRIs in AD the expected pathological change rates are generally mild and slowly varying across the brain. Second, a central assumption made in this paper is that the spatial dependencies of the signal are local, i.e. that the image intensities are smoothly varying and correlated within a spatial neighborhood of radius 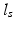 . We note that our assumptions about separability and stationarity are compatible with the spatio-temporal correlation models commonly assumed by registration-based approaches.
. We note that our assumptions about separability and stationarity are compatible with the spatio-temporal correlation models commonly assumed by registration-based approaches.
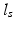 . We note that our assumptions about separability and stationarity are compatible with the spatio-temporal correlation models commonly assumed by registration-based approaches.
. We note that our assumptions about separability and stationarity are compatible with the spatio-temporal correlation models commonly assumed by registration-based approaches.A reasonable choice for such a local spatial covariance structure is a negative squared exponential model 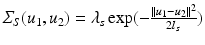 , where
, where 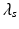 is the global spatial amplitude parameter, and
is the global spatial amplitude parameter, and 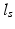 is the length-scale of the Gaussian spatial neighborhood. We observe that such a covariance structure is stationary with respect to the space parameters. Furthermore we can exploit the separability properties of the negative exponential function to note that given two separate spatial locations
is the length-scale of the Gaussian spatial neighborhood. We observe that such a covariance structure is stationary with respect to the space parameters. Furthermore we can exploit the separability properties of the negative exponential function to note that given two separate spatial locations 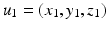 and
and 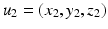 we have
we have
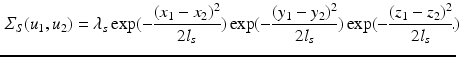 For this reason the covariance matrix
For this reason the covariance matrix 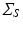 can be further decomposed as the Kronecker product of covariance matrices of 1-dimensional processes:
can be further decomposed as the Kronecker product of covariance matrices of 1-dimensional processes: 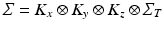 . We observe that the model is here conveniently represented by the product of independent covariances of significantly smaller size, and is completely identified by the spatial, temporal and noise parameters. In particular the proposed model is flexible with respect to the temporal covariance matrix
. We observe that the model is here conveniently represented by the product of independent covariances of significantly smaller size, and is completely identified by the spatial, temporal and noise parameters. In particular the proposed model is flexible with respect to the temporal covariance matrix 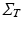 , which can be expressed in terms of complex mixed-effects structure, and can account for covariates and different progression models. For instance, in this work the matrix
, which can be expressed in terms of complex mixed-effects structure, and can account for covariates and different progression models. For instance, in this work the matrix 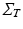 is first specified in order to model the temporal progression observed in time series of images (Sect. 4), and then is used to model the influence of anatomical, genetic, clinical, and sociodemographic covariates on individual atrophy rates modelled by non-linear registration (Sect. 5).
is first specified in order to model the temporal progression observed in time series of images (Sect. 4), and then is used to model the influence of anatomical, genetic, clinical, and sociodemographic covariates on individual atrophy rates modelled by non-linear registration (Sect. 5).
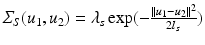 , where
, where 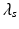 is the global spatial amplitude parameter, and
is the global spatial amplitude parameter, and 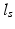 is the length-scale of the Gaussian spatial neighborhood. We observe that such a covariance structure is stationary with respect to the space parameters. Furthermore we can exploit the separability properties of the negative exponential function to note that given two separate spatial locations
is the length-scale of the Gaussian spatial neighborhood. We observe that such a covariance structure is stationary with respect to the space parameters. Furthermore we can exploit the separability properties of the negative exponential function to note that given two separate spatial locations 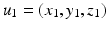 and
and 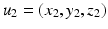 we have
we have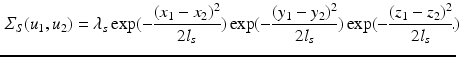
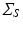 can be further decomposed as the Kronecker product of covariance matrices of 1-dimensional processes:
can be further decomposed as the Kronecker product of covariance matrices of 1-dimensional processes: 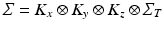 . We observe that the model is here conveniently represented by the product of independent covariances of significantly smaller size, and is completely identified by the spatial, temporal and noise parameters. In particular the proposed model is flexible with respect to the temporal covariance matrix
. We observe that the model is here conveniently represented by the product of independent covariances of significantly smaller size, and is completely identified by the spatial, temporal and noise parameters. In particular the proposed model is flexible with respect to the temporal covariance matrix 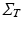 , which can be expressed in terms of complex mixed-effects structure, and can account for covariates and different progression models. For instance, in this work the matrix
, which can be expressed in terms of complex mixed-effects structure, and can account for covariates and different progression models. For instance, in this work the matrix 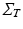 is first specified in order to model the temporal progression observed in time series of images (Sect. 4), and then is used to model the influence of anatomical, genetic, clinical, and sociodemographic covariates on individual atrophy rates modelled by non-linear registration (Sect. 5).
is first specified in order to model the temporal progression observed in time series of images (Sect. 4), and then is used to model the influence of anatomical, genetic, clinical, and sociodemographic covariates on individual atrophy rates modelled by non-linear registration (Sect. 5).3 Inference in Gaussian Processes with Kronecker Structure
The GP-based generative model with Kronecker covariance structure outlined in this work provides a powerful and efficient framework for prediction using image time series. Here we provide the main results concerning the marginal likelihood computation, the hyper-parameter optimization and the posterior prediction.
Let 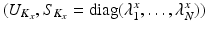 and
and 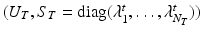 be the eigenvectors and eigenvalues associated to the one-dimensional spatial and temporal covariance matrices
be the eigenvectors and eigenvalues associated to the one-dimensional spatial and temporal covariance matrices 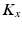 and
and 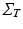 . This eigendecomposition problem can be easily and efficiently solved beforehand offline. We further introduce the shortform notation
. This eigendecomposition problem can be easily and efficiently solved beforehand offline. We further introduce the shortform notation 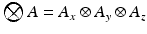 .
.
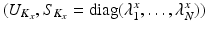 and
and 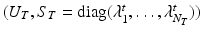 be the eigenvectors and eigenvalues associated to the one-dimensional spatial and temporal covariance matrices
be the eigenvectors and eigenvalues associated to the one-dimensional spatial and temporal covariance matrices 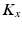 and
and 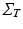 . This eigendecomposition problem can be easily and efficiently solved beforehand offline. We further introduce the shortform notation
. This eigendecomposition problem can be easily and efficiently solved beforehand offline. We further introduce the shortform notation 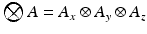 .
.Log-Marginal Likelihood. The marginal likelihood of the model (1) is the following:
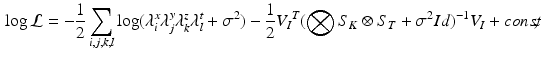
with 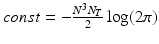 ,
, ![$$ V_I = {\text {vec}}\left[ (U_{K_z}^T \otimes U_{T}^T) \tilde{I} (U_{K_x} \otimes U_{K_y})\right] $$](/wp-content/uploads/2016/09/A339424_1_En_49_Chapter_IEq26.gif) , and where
, and where 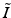 is the matricization of I into a 2 dimensional matrix of dimension
is the matricization of I into a 2 dimensional matrix of dimension 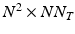 , and
, and 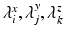 and
and 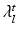 are the eigenvalues of respectively
are the eigenvalues of respectively 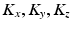 and
and 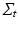 . The computation of the vector
. The computation of the vector 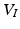 requires the storage and multiplication of matrices of relatively small sizes, respectively
requires the storage and multiplication of matrices of relatively small sizes, respectively 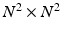 ,
, 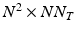 and
and 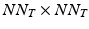 . The product
. The product 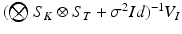 can be finally computed as the solution of the linear system
can be finally computed as the solution of the linear system 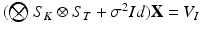 , which is straightforward since
, which is straightforward since 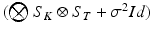 is diagonal.
is diagonal.
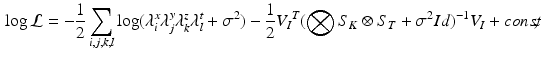
(2)
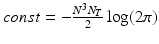 ,
, ![$$ V_I = {\text {vec}}\left[ (U_{K_z}^T \otimes U_{T}^T) \tilde{I} (U_{K_x} \otimes U_{K_y})\right] $$](/wp-content/uploads/2016/09/A339424_1_En_49_Chapter_IEq26.gif) , and where
, and where 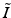 is the matricization of I into a 2 dimensional matrix of dimension
is the matricization of I into a 2 dimensional matrix of dimension 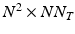 , and
, and 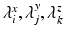 and
and 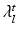 are the eigenvalues of respectively
are the eigenvalues of respectively 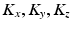 and
and 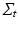 . The computation of the vector
. The computation of the vector 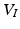 requires the storage and multiplication of matrices of relatively small sizes, respectively
requires the storage and multiplication of matrices of relatively small sizes, respectively 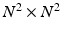 ,
, 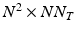 and
and 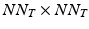 . The product
. The product 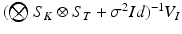 can be finally computed as the solution of the linear system
can be finally computed as the solution of the linear system 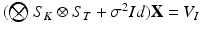 , which is straightforward since
, which is straightforward since 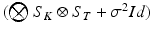 is diagonal.
is diagonal.Hyperparameter Optimization. The derivative of the log-likelihood (2) with respect to the model parameters 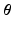 is:
is:
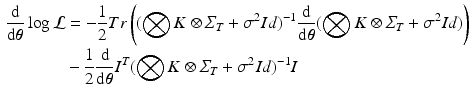
It can be shown that formula (3) can be efficiently computed with respect to each model parameters. For instance, the gradient with respect to the noise parameter can be expressed in the form:
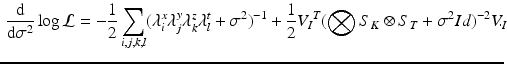
Prediction. A major strength of a GP framework for image time series is that it easily enables probabilistic predictions based on given observations. The proposed generative model allows us to consider the predictive distributions of the latent spatio-temporal process at any testing locations 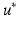 and timepoints
and timepoints 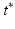 . Given image time series I(u, t), we now aim at predicting the image
. Given image time series I(u, t), we now aim at predicting the image 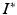 at
at 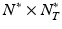 testing coordinates
testing coordinates 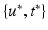 . Let us define
. Let us define 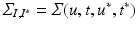 the cross-covariance matrix of training and testing data, and
the cross-covariance matrix of training and testing data, and 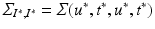 the covariance evaluated on the new coordinates. The joint GP model of training and testing data is:
the covariance evaluated on the new coordinates. The joint GP model of training and testing data is:
![$$\begin{aligned} \begin{pmatrix}I(u,t)\\ I^*(u^*,t^*) \end{pmatrix}\sim & {} \mathcal {N}\left[ \left( \begin{array}{c} 0\\ 0 \end{array}\right) ,\left( \begin{array}{cc} \varSigma +\sigma ^2 Id&{} \varSigma _{I,I^*}\\ \varSigma _{I^*,I} &{} \varSigma _{I^*,I^*}+\sigma ^2 Id \end{array}\right) \right] \!\!\!\!\!, \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_49_Chapter_Equ5.gif)
and it can be easily shown that the posterior distribution of 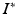 conditioned on the observed time series I and parameters
conditioned on the observed time series I and parameters 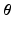 is [11]:
is [11]:
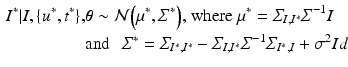
From the practical perspective, we notice that by definition the new covariance matrices still have a Kronecker product form: 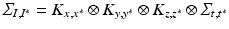 , and
, and 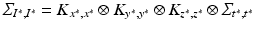 . The predicted mean
. The predicted mean 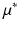 at coordinates
at coordinates 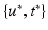 is then
is then
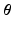 is:
is: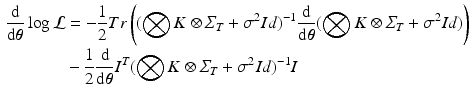
(3)
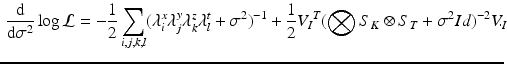
(4)
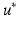 and timepoints
and timepoints 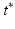 . Given image time series I(u, t), we now aim at predicting the image
. Given image time series I(u, t), we now aim at predicting the image 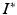 at
at 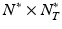 testing coordinates
testing coordinates 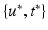 . Let us define
. Let us define 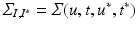 the cross-covariance matrix of training and testing data, and
the cross-covariance matrix of training and testing data, and 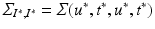 the covariance evaluated on the new coordinates. The joint GP model of training and testing data is:
the covariance evaluated on the new coordinates. The joint GP model of training and testing data is:![$$\begin{aligned} \begin{pmatrix}I(u,t)\\ I^*(u^*,t^*) \end{pmatrix}\sim & {} \mathcal {N}\left[ \left( \begin{array}{c} 0\\ 0 \end{array}\right) ,\left( \begin{array}{cc} \varSigma +\sigma ^2 Id&{} \varSigma _{I,I^*}\\ \varSigma _{I^*,I} &{} \varSigma _{I^*,I^*}+\sigma ^2 Id \end{array}\right) \right] \!\!\!\!\!, \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_49_Chapter_Equ5.gif)
(5)
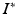 conditioned on the observed time series I and parameters
conditioned on the observed time series I and parameters 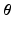 is [11]:
is [11]: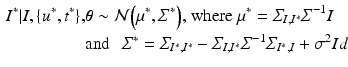
(6)
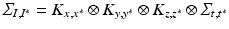 , and
, and 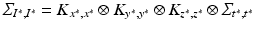 . The predicted mean
. The predicted mean 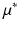 at coordinates
at coordinates 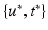 is then
is then