2 2 mm
2 mm to 1
to 1 1
1 1 mm
1 mm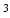 requires 128 times more imaging time at equal SNR; a 5 min. acquisition would thus become a 10.7 h. acquisition, which is not realistic.
requires 128 times more imaging time at equal SNR; a 5 min. acquisition would thus become a 10.7 h. acquisition, which is not realistic.
Enhancing the spatial resolution requires sampling of higher frequencies in k-space which is very challenging to accomplish with high SNR and short acquisition duration time. Instead of acquiring high frequencies along all the axes simultaneously, [8] demonstrated that high-resolution (HR) k-space sampling for a diffusion gradient can be achieved by imaging this diffusion gradient with a series of anisotropically oversampled acquisitions (so-called “snapshots”) that each densely samples more frequencies along a limited number of axes (one or two). Compared to full, dense HR sampling, this multi-snapshot non-Cartesian sampling reduces the spatial encoding burden and provides substantially increased SNR for each snapshot due to the larger voxel size. In [8], an image generation model was then employed to describe how the anisotropic low resolution (LR) snapshots are observations of the unknown, underlying HR isotropic DW images we aim to recover (forward model), and the corresponding HR DW images recovered by inversing this forward model. A similar technique was later employed in [6]. A particular strength of this approach is that it only requires a conventional DW-MRI sequence and is therefore straightforward to implement. When using three orthogonal snapshots for each diffusion gradient, this effectively enhances spatial resolution along all the axes (x,y,z) while providing an 8x theoretical reduction in imaging time compared to conventional sampling at equal SNR [8].
A major limitation in [6, 8] is that each DW image was reconstructed separately. First, the fact that the DWIs constitute different views of the same anatomy was ignored. DW images are coupled and this correlation of information can be leveraged by introducing in the reconstruction the knowledge of the local tissue microstructure. Second, an isotropic HR gradient image could not be recovered if one of its snapshots was missing, for example because of intra-scan motion, even if other snapshots for this gradient were successfully acquired.
Tobisch et al. [12] built upon the work in [6, 8] and proposed to introduce an ad-hoc coupling between HR reconstruction and tissue model estimation to capture the coupling between DW images. They considered the ball-and-stick tissue model at each voxel, thereby assuming (1) the presence of a single fascicle in each voxel; (2) the absence of radial diffusivity; and (3) a prefixed axial diffusivity value constant for the entire brain. This model, however, poorly represents in vivo brain tissues. This is critical because, when HR reconstruction and tissue model estimation are coupled, the ability of the tissue model to accurately predict the DW signal for a diffusion gradient conditions the ultimate HR reconstruction accuracy. In [12], only results with synthetic simulations were reported, but no evidence of the technical efficacy of the technique was reported with in vivo data. More importantly, and similarly to [6, 8], this technique required the successful acquisition of all the snapshots for a diffusion gradient to reconstruct the corresponding HR gradient image.
In this work, we propose a novel multi-snapshot DWI reconstruction technique that simultaneously achieves HR reconstruction and tissue model estimation while enabling reconstruction with missing snapshots. Instead of an ad-hoc coupling [12], our approach is formalized as a joint probabilistic model with missing observations, from which interactions between missing snapshots, HR reconstruction and a generic tissue model naturally emerge. We describe the tissue microstructure at a voxel with a diffusion compartment imaging (DCI) tissue model that reflects the presence of tissue compartments in each voxel, providing a model-based description of the signal attenuation for any diffusion gradient orientation and strength. Our novel Simultaneous multi-snapsHot highresOlution ReconsTruCtion and diffUsion comparTment imaging (SHORTCUT) approach enables reconstruction from snapshots with different subsets of gradients, providing increased robustness to patient motion and potential for acceleration. We evaluate SHORTCUT with synthetic simulations, simulated multi-snapshot scenario and in vivo multi-snapshot imaging. We investigate the robustness to missing snapshots. We show that SHORTCUT enables both better reconstruction of each DW image and better estimation of the tissue parameters.
2 Theory
2.1 The SHORTCUT Framework
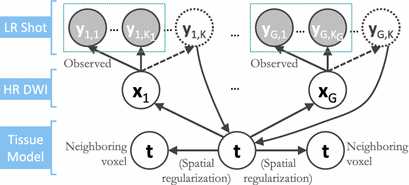
We formalize SHORTCUT as a joint probabilistic model synthetized in Fig. 1. We consider G unique diffusion gradients and a maximum of K snapshots per gradient. We denote by 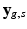 the DW image for the snapshot s of the diffusion gradient g and by
the DW image for the snapshot s of the diffusion gradient g and by 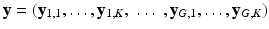 the images of the K G snapshots in which only
the images of the K G snapshots in which only 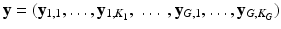 have been acquired and
have been acquired and 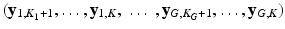 are missing. We denote by
are missing. We denote by 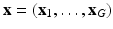 the unknown HR DW images we aim to recover. We also consider a generic DCI tissue model dependent on some parameters
the unknown HR DW images we aim to recover. We also consider a generic DCI tissue model dependent on some parameters 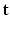 that describes the DW signal attenuation at a voxel i for a diffusion gradient g by
that describes the DW signal attenuation at a voxel i for a diffusion gradient g by 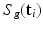 . We aim at recovering (1) the series of missing snapshots; (2) the series of unknown HR DW images
. We aim at recovering (1) the series of missing snapshots; (2) the series of unknown HR DW images 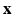 ; (3) the parameters
; (3) the parameters 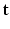 of the tissue model at each voxel. The simultaneous estimation of
of the tissue model at each voxel. The simultaneous estimation of 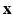 ,
, 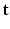 ,
, 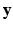 is performed according to the maximum a posteriori principle, by maximizing:
is performed according to the maximum a posteriori principle, by maximizing:
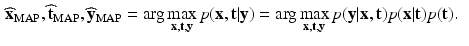
Factor 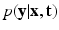 . The likelihood
. The likelihood 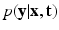 describes the probability of observing the snapshots
describes the probability of observing the snapshots 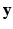 given a realization of
given a realization of 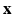 and
and 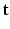 and relates to HR reconstruction. Assuming conditional independence we can show that:
and relates to HR reconstruction. Assuming conditional independence we can show that:
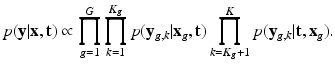
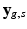 the DW image for the snapshot s of the diffusion gradient g and by
the DW image for the snapshot s of the diffusion gradient g and by 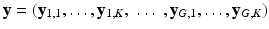 the images of the K G snapshots in which only
the images of the K G snapshots in which only 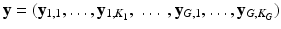 have been acquired and
have been acquired and 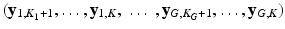 are missing. We denote by
are missing. We denote by 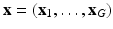 the unknown HR DW images we aim to recover. We also consider a generic DCI tissue model dependent on some parameters
the unknown HR DW images we aim to recover. We also consider a generic DCI tissue model dependent on some parameters 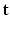 that describes the DW signal attenuation at a voxel i for a diffusion gradient g by
that describes the DW signal attenuation at a voxel i for a diffusion gradient g by 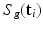 . We aim at recovering (1) the series of missing snapshots; (2) the series of unknown HR DW images
. We aim at recovering (1) the series of missing snapshots; (2) the series of unknown HR DW images 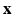 ; (3) the parameters
; (3) the parameters 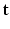 of the tissue model at each voxel. The simultaneous estimation of
of the tissue model at each voxel. The simultaneous estimation of 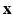 ,
, 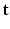 ,
, 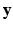 is performed according to the maximum a posteriori principle, by maximizing:
is performed according to the maximum a posteriori principle, by maximizing: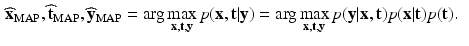
(1)
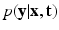 . The likelihood
. The likelihood 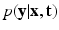 describes the probability of observing the snapshots
describes the probability of observing the snapshots 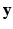 given a realization of
given a realization of 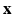 and
and 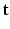 and relates to HR reconstruction. Assuming conditional independence we can show that:
and relates to HR reconstruction. Assuming conditional independence we can show that: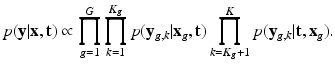

Fig. 1.
Graphical representation of the SHORTCUT joint model in which we consider that some gradients may not be acquired in all snapshots.
For acquired DW images (i.e., ![$$k \in [1, K_g]$$](/wp-content/uploads/2016/09/A339424_1_En_6_Chapter_IEq24.gif) ), we consider that all the information about
), we consider that all the information about 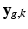 is contained in the HR image
is contained in the HR image 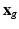 . The term
. The term 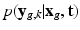 then describes how each snapshot constitutes an observation of the unknown
then describes how each snapshot constitutes an observation of the unknown 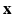 . Similarly to [8], we consider an image generation model that describes how the LR snapshots are obtained from the unknown underlying HR volumes. Specifically, for each diffusion gradient g, we consider that
. Similarly to [8], we consider an image generation model that describes how the LR snapshots are obtained from the unknown underlying HR volumes. Specifically, for each diffusion gradient g, we consider that 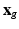 goes through geometric and signal modifying operations to generate the K acquired LR volume:
goes through geometric and signal modifying operations to generate the K acquired LR volume: 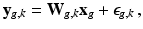 where
where 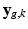 and
and 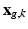 are expressed as column vectors by a lexicographical reordering of the pixels. We consider
are expressed as column vectors by a lexicographical reordering of the pixels. We consider 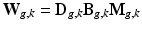 where
where 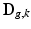 is the down-sampling matrix,
is the down-sampling matrix, 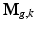 is the warping matrix that maps the HR volume
is the warping matrix that maps the HR volume 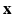 to the LR volume
to the LR volume 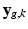 ,
, 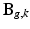 describes the point spread function (PSF) of the MRI signal acquisition process and
describes the point spread function (PSF) of the MRI signal acquisition process and 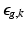 is the vector of residual noise. We assume that, conditionally on
is the vector of residual noise. We assume that, conditionally on 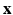 , the LR data
, the LR data 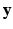 are normally distributed around the unknown HR intensities with variance
are normally distributed around the unknown HR intensities with variance 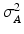 , so that:
, so that:
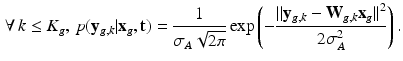
For non-acquired images (i.e., ![$$k \in [ K_g +1 , K] $$](/wp-content/uploads/2016/09/A339424_1_En_6_Chapter_IEq43.gif) ) the term
) the term 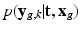 describes the agreement between the missing snapshot
describes the agreement between the missing snapshot 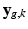 and the signal arising from the DCI model for the unobserved
and the signal arising from the DCI model for the unobserved 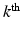 snapshot of the gradient g. This term relates to the missing snapshot recovery using the tissue model. We consider that all the information about
snapshot of the gradient g. This term relates to the missing snapshot recovery using the tissue model. We consider that all the information about 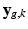 is contained in
is contained in 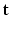 and assume that, conditionally on
and assume that, conditionally on 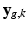 , the intensities of the missing snapshot
, the intensities of the missing snapshot 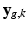 are normally distributed around the intensities of the recovered LR snapshot
are normally distributed around the intensities of the recovered LR snapshot 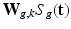 with variance
with variance 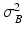 :
:
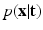 . The term
. The term 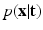 describes the agreement between the series of DW images
describes the agreement between the series of DW images 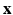 and the HR signal modeled by the tissue model and relates to the DCI model estimation. We consider that the HR image domain
and the HR signal modeled by the tissue model and relates to the DCI model estimation. We consider that the HR image domain 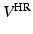 is a regular 3-dimensional (3D) grid and denote by
is a regular 3-dimensional (3D) grid and denote by 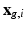 the
the 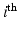 voxel of the
voxel of the 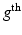 HR DW image
HR DW image 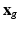 . We assume that, conditionally on
. We assume that, conditionally on 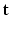 , the HR DW images
, the HR DW images 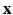 are normally distributed around the unknown modeled signal
are normally distributed around the unknown modeled signal 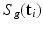 with variance
with variance 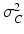 :
:
Get Clinical Tree app for offline access

![$$k \in [1, K_g]$$](/wp-content/uploads/2016/09/A339424_1_En_6_Chapter_IEq24.gif) ), we consider that all the information about
), we consider that all the information about 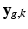 is contained in the HR image
is contained in the HR image 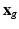 . The term
. The term 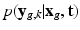 then describes how each snapshot constitutes an observation of the unknown
then describes how each snapshot constitutes an observation of the unknown 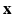 . Similarly to [8], we consider an image generation model that describes how the LR snapshots are obtained from the unknown underlying HR volumes. Specifically, for each diffusion gradient g, we consider that
. Similarly to [8], we consider an image generation model that describes how the LR snapshots are obtained from the unknown underlying HR volumes. Specifically, for each diffusion gradient g, we consider that 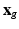 goes through geometric and signal modifying operations to generate the K acquired LR volume:
goes through geometric and signal modifying operations to generate the K acquired LR volume: 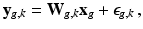 where
where 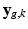 and
and 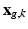 are expressed as column vectors by a lexicographical reordering of the pixels. We consider
are expressed as column vectors by a lexicographical reordering of the pixels. We consider 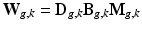 where
where 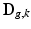 is the down-sampling matrix,
is the down-sampling matrix, 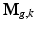 is the warping matrix that maps the HR volume
is the warping matrix that maps the HR volume 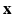 to the LR volume
to the LR volume 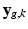 ,
, 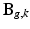 describes the point spread function (PSF) of the MRI signal acquisition process and
describes the point spread function (PSF) of the MRI signal acquisition process and 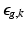 is the vector of residual noise. We assume that, conditionally on
is the vector of residual noise. We assume that, conditionally on 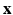 , the LR data
, the LR data 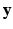 are normally distributed around the unknown HR intensities with variance
are normally distributed around the unknown HR intensities with variance 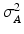 , so that:
, so that: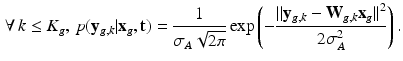
(2)
![$$k \in [ K_g +1 , K] $$](/wp-content/uploads/2016/09/A339424_1_En_6_Chapter_IEq43.gif) ) the term
) the term 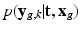 describes the agreement between the missing snapshot
describes the agreement between the missing snapshot 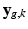 and the signal arising from the DCI model for the unobserved
and the signal arising from the DCI model for the unobserved 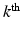 snapshot of the gradient g. This term relates to the missing snapshot recovery using the tissue model. We consider that all the information about
snapshot of the gradient g. This term relates to the missing snapshot recovery using the tissue model. We consider that all the information about 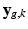 is contained in
is contained in 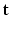 and assume that, conditionally on
and assume that, conditionally on 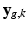 , the intensities of the missing snapshot
, the intensities of the missing snapshot 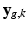 are normally distributed around the intensities of the recovered LR snapshot
are normally distributed around the intensities of the recovered LR snapshot 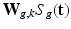 with variance
with variance 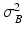 :
: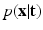 . The term
. The term 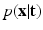 describes the agreement between the series of DW images
describes the agreement between the series of DW images 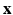 and the HR signal modeled by the tissue model and relates to the DCI model estimation. We consider that the HR image domain
and the HR signal modeled by the tissue model and relates to the DCI model estimation. We consider that the HR image domain 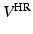 is a regular 3-dimensional (3D) grid and denote by
is a regular 3-dimensional (3D) grid and denote by 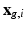 the
the 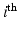 voxel of the
voxel of the 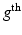 HR DW image
HR DW image 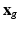 . We assume that, conditionally on
. We assume that, conditionally on 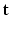 , the HR DW images
, the HR DW images 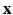 are normally distributed around the unknown modeled signal
are normally distributed around the unknown modeled signal 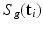 with variance
with variance 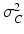 :
: