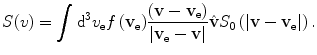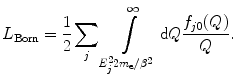(1)
Amersham, Buckinghamshire, UK
12.2 Stopping Number
12.2.1 Definition
12.2.3 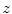 -Dependent Stopping Number,
-Dependent Stopping Number, 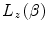
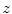 -Dependent Stopping Number,
-Dependent Stopping Number, 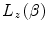
12.3.1 Introductory Comments
12.3.3 Quantum-Mechanical Theory
12.3.5 Parameterisation of 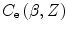
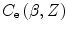
12.4.1 Introductory Comments
12.4.2 Electronic Polarisation
12.4.6 Čerenkov Radiation
12.5.1 History
12.5.3 Additional Comments
12.6.1 Introduction
12.6.2 Derivation
Abstract
The development of the collision stopping power to this point has been based upon the use of the first term of the Born series, or the first Born approximation. Associated with this have been a number of simplifications and approximations: in particular, the collision stopping power is proportional to the square of the projectile’s charge, the atomic electrons are effectively stationary in the reference frame of the projectile and the projectile does not polarise the medium. In this chapter, we derive a variety of correction factors to be applied to our results obtained so far. We do so in the context of the stopping number which is considered as an expansion of the collision stopping. The zeroth-order (or kinematic) term is that of Chap. 10, and additional corrections are treated as higher-order perturbations. Corrections for nonnegligible atomic electron motion and medium polarisation are independent of the projectile’s charge. Additional perturbations are in powers of this charge and are the Barkas–Andersen effects and the Bloch correction.
12.1 Introductory Comments
We have derived the soft- and hard-collision stopping powers, combined them to yield the total collision stopping power and have derived the expenditure of energetic charged particle energy required to yield ionisation. These results have been built upon the foundation of the first term of the Born series applied to a simple model of the medium composed of a cold and dilute monoatomic gas. To extend this to realistic cases, we must consider the inclusion of additional terms, or correction factors, to account for changes in the calculated stopping power caused by realistic situations. We may thus consider the collision stopping power expression derived in Chap. 10 as being a zeroth-order result.
This chapter presents these additional correction factors which contribute to the stopping power expression so as to correct for the simplifying assumptions used in its derivation. In effect, these additional terms may be considered as being perturbative in that they are small in magnitude corrections proportional to powers of the projectile’s electric charge (up to second order).1 These factors account for the physics neglected in our derivation so far: atomic electron motion, a condensed medium and the Bloch correction. In order to place the derivations of these higher order into an organised fashion, we introduce the concept of the stopping number, a dimensionless entity of which we have already derived its zeroth-order term in Chap. 10.
12.2 Stopping Number
12.2.1 Definition
A useful means of combining the additional correction terms with the expression of the collision stopping power is through the definition of the stopping number. Consider the expression for the mass collision stopping power, disregarding projectile spin, given by (10.3). We can write it in the following general form:
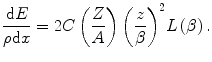
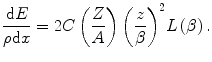
(12.1)
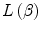 is known as the stopping number because it is a dimensionless modifier of
is known as the stopping number because it is a dimensionless modifier of 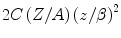 . We shall write it as the summation of three further dimensionless terms, each weighted by powers of the projectile electric charge (normalised to the unit charge, e), and which may be considered as a perturbative expression. That is,
. We shall write it as the summation of three further dimensionless terms, each weighted by powers of the projectile electric charge (normalised to the unit charge, e), and which may be considered as a perturbative expression. That is,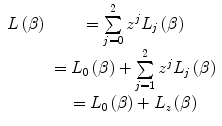
(12.2)
We can see from (10.3) that the zeroth-order term of this expansion (i.e. with no explicit dependence), 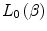 , can itself be written as a series
, can itself be written as a series
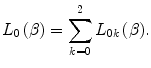
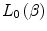 , can itself be written as a series
, can itself be written as a series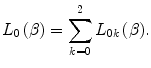
(12.3)
We now identify the individual terms within these summations.
12.2.2 Zeroth-Order Stopping Number, 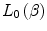
This summation contains three terms. The first is the kinematical term which was derived in our application of the first-order term of the Born expansion to the theoretical development of the collision stopping power. The second accounts for the effects of atomic electron motion. The third includes the perturbative effects of the surrounding medium upon the projectile’s electric field and the resulting reduction in its electric field leading to a subsequent decrease in the stopping power.
12.2.2.1 Kinematical Term 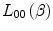
This term is dependent solely upon the kinematics of the projectile and the mean excitation energy of the medium, which was the topic of Chap. 11.
This is the only term in the stopping power expression developed on the basis of the assumptions outlined in Sect. 12.1.
12.2.2.2 Atomic Electron Motion Term 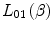
The next term in 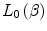 corrects for the fact that the derivation of the Bethe soft-collision stopping power had assumed that the projectile velocity is much greater than those of the orbiting atomic electrons. This led to the kinematical approximation that the target electron was at rest. But, as the projectile decelerates, its velocity eventually becomes comparable to those of the atomic electrons, and the validity of this assumption becomes increasingly untenable. Consequently, an additional factor must be added to correct for this:
corrects for the fact that the derivation of the Bethe soft-collision stopping power had assumed that the projectile velocity is much greater than those of the orbiting atomic electrons. This led to the kinematical approximation that the target electron was at rest. But, as the projectile decelerates, its velocity eventually becomes comparable to those of the atomic electrons, and the validity of this assumption becomes increasingly untenable. Consequently, an additional factor must be added to correct for this:
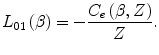
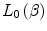 corrects for the fact that the derivation of the Bethe soft-collision stopping power had assumed that the projectile velocity is much greater than those of the orbiting atomic electrons. This led to the kinematical approximation that the target electron was at rest. But, as the projectile decelerates, its velocity eventually becomes comparable to those of the atomic electrons, and the validity of this assumption becomes increasingly untenable. Consequently, an additional factor must be added to correct for this:
corrects for the fact that the derivation of the Bethe soft-collision stopping power had assumed that the projectile velocity is much greater than those of the orbiting atomic electrons. This led to the kinematical approximation that the target electron was at rest. But, as the projectile decelerates, its velocity eventually becomes comparable to those of the atomic electrons, and the validity of this assumption becomes increasingly untenable. Consequently, an additional factor must be added to correct for this: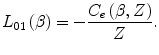
(12.5)
We will refer to 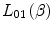 as the atomic electron motion term and to
as the atomic electron motion term and to 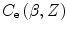 as the atomic shell correction term so as to be consistent with use in the literature.
as the atomic shell correction term so as to be consistent with use in the literature. 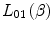 will be derived in Sect. 12.3.
will be derived in Sect. 12.3.
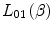 as the atomic electron motion term and to
as the atomic electron motion term and to 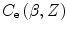 as the atomic shell correction term so as to be consistent with use in the literature.
as the atomic shell correction term so as to be consistent with use in the literature. 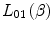 will be derived in Sect. 12.3.
will be derived in Sect. 12.3.12.2.2.3 Condensed Medium Term 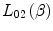
The next term in 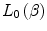 allows the stopping power calculation to be applied to a condensed medium by correcting for the assumption that the medium is a cold dilute gas in which case, the energetic charged projectile interacts with a single atom at a time. On the other hand, in a condensed medium, such as tissue, the Coulomb field of the charged projectile will interact with multiple atoms leading to the polarisation of the medium resulting in a reduction of the penetration of the electric field. With this reduction of the electric field, the collision stopping power will be diminished. The form of this factor is conventionally given in the form of
allows the stopping power calculation to be applied to a condensed medium by correcting for the assumption that the medium is a cold dilute gas in which case, the energetic charged projectile interacts with a single atom at a time. On the other hand, in a condensed medium, such as tissue, the Coulomb field of the charged projectile will interact with multiple atoms leading to the polarisation of the medium resulting in a reduction of the penetration of the electric field. With this reduction of the electric field, the collision stopping power will be diminished. The form of this factor is conventionally given in the form of
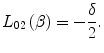
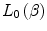 allows the stopping power calculation to be applied to a condensed medium by correcting for the assumption that the medium is a cold dilute gas in which case, the energetic charged projectile interacts with a single atom at a time. On the other hand, in a condensed medium, such as tissue, the Coulomb field of the charged projectile will interact with multiple atoms leading to the polarisation of the medium resulting in a reduction of the penetration of the electric field. With this reduction of the electric field, the collision stopping power will be diminished. The form of this factor is conventionally given in the form of
allows the stopping power calculation to be applied to a condensed medium by correcting for the assumption that the medium is a cold dilute gas in which case, the energetic charged projectile interacts with a single atom at a time. On the other hand, in a condensed medium, such as tissue, the Coulomb field of the charged projectile will interact with multiple atoms leading to the polarisation of the medium resulting in a reduction of the penetration of the electric field. With this reduction of the electric field, the collision stopping power will be diminished. The form of this factor is conventionally given in the form of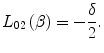
(12.6)
We will refer to 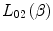 as the condensed medium term and to δ as the density effect term so as to maintain consistency with the literature
as the condensed medium term and to δ as the density effect term so as to maintain consistency with the literature 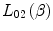 , and the physics of the polarisability of a medium by an energetic charged particle is the topic of Sect. 12.4.
, and the physics of the polarisability of a medium by an energetic charged particle is the topic of Sect. 12.4.
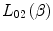 as the condensed medium term and to δ as the density effect term so as to maintain consistency with the literature
as the condensed medium term and to δ as the density effect term so as to maintain consistency with the literature 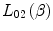 , and the physics of the polarisability of a medium by an energetic charged particle is the topic of Sect. 12.4.
, and the physics of the polarisability of a medium by an energetic charged particle is the topic of Sect. 12.4.12.2.3 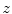 -Dependent Stopping Number,
-Dependent Stopping Number, 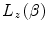
12.2.3.1 Barkas–Andersen Term 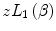
As to be discussed in Sect. 12.5, it was discovered experimentally during the 1950s that the range (i.e. the integration of the reciprocal of the stopping power over energy and the topic of Chap. 13) of a particle differed minutely from that of its antiparticle. This is known as the Barkas–Andersen effect in which the stopping power for a positively charged particle is slightly greater than that for a negatively charged particle with the same mass and velocity (i.e. its antiparticle with the same kinetic energy).
This discovery led to the realisation that the collision stopping power had to have a dependence upon the sign of the projectile’s electric charge, whereas the stopping power derivations yielded a 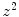 dependence only. That is, it must include a perturbative effect proportional to z n , where n is an odd integer. Hence, the first term in
dependence only. That is, it must include a perturbative effect proportional to z n , where n is an odd integer. Hence, the first term in 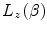 is
is 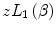 . The perturbative term is dimensionless, and the multiplier z which, when combined with the
. The perturbative term is dimensionless, and the multiplier z which, when combined with the 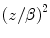 term in the multiplier of (12.1), produces a contribution to the collision stopping power that is proportional to
term in the multiplier of (12.1), produces a contribution to the collision stopping power that is proportional to 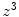 and, thus, a dependence upon the sign of the projectile’s charge.
and, thus, a dependence upon the sign of the projectile’s charge.
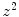 dependence only. That is, it must include a perturbative effect proportional to z n , where n is an odd integer. Hence, the first term in
dependence only. That is, it must include a perturbative effect proportional to z n , where n is an odd integer. Hence, the first term in 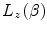 is
is 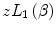 . The perturbative term is dimensionless, and the multiplier z which, when combined with the
. The perturbative term is dimensionless, and the multiplier z which, when combined with the 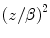 term in the multiplier of (12.1), produces a contribution to the collision stopping power that is proportional to
term in the multiplier of (12.1), produces a contribution to the collision stopping power that is proportional to 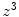 and, thus, a dependence upon the sign of the projectile’s charge.
and, thus, a dependence upon the sign of the projectile’s charge.12.2.3.2 Bloch Correction Term 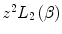
As described in Chaps. 1 and 8, the first third of the twentieth century presented two theories of the soft-collision stopping power – that derived by Bohr from classical mechanics and that derived by Bethe from quantum mechanics. Despite the vastly differing starting points, as exemplified, for example, by the use of impact parameter by Bohr and the use of the Born approximation and momentum/energy transfer by Bethe, the results of both theories were so similar that the consideration of ‘bridging’ between the two had to have been had. This was done by Bloch, and this resulted in a term within the associated correction term proportional to 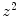 to lead to an overall
to lead to an overall 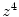 dependence in the collision stopping power. We extend our earlier discussion of Chap. 8 of the Bloch correction term in Sect. 12.6.
dependence in the collision stopping power. We extend our earlier discussion of Chap. 8 of the Bloch correction term in Sect. 12.6.
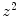 to lead to an overall
to lead to an overall 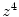 dependence in the collision stopping power. We extend our earlier discussion of Chap. 8 of the Bloch correction term in Sect. 12.6.
dependence in the collision stopping power. We extend our earlier discussion of Chap. 8 of the Bloch correction term in Sect. 12.6.12.3 Atomic Electron Motion Term, 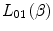
12.3.1 Introductory Comments
Our derivations of the collision stopping power have ignored the orbital velocities of the atomic electrons within the medium by assuming implicitly that the projectile velocity far exceeds that of the atomic electron. That is, in terms of the kinematics of the collision, the electron is considered to be at rest. This assumption is usually valid for a fast projectile and a low-Z atom. However, it begins to break down as the projectile decelerates to velocities approaching those of the orbital electrons or for the case of high-Z atoms where the orbital velocities can approach significant fractions of the speed of light. Thus, a kinematical correction is required, through 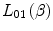 , to account for the change in the collision stopping power induced by the nonnegligible orbital velocities.
, to account for the change in the collision stopping power induced by the nonnegligible orbital velocities.
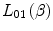 , to account for the change in the collision stopping power induced by the nonnegligible orbital velocities.
, to account for the change in the collision stopping power induced by the nonnegligible orbital velocities.Clearly, the correction factor, as a function of projectile velocity, will change as the projectile decelerates. The K-shell electrons will be affected first as these are the most tightly bound and have the highest orbital velocities. These will then be followed by contributions related to the L- and M-shell electrons. 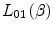 leads to a reduction in the stopping power as will be shown although the magnitude of the correction is rather small (a few percent) for low atomic number media, but increases considerably for high-Z media.
leads to a reduction in the stopping power as will be shown although the magnitude of the correction is rather small (a few percent) for low atomic number media, but increases considerably for high-Z media.
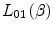 leads to a reduction in the stopping power as will be shown although the magnitude of the correction is rather small (a few percent) for low atomic number media, but increases considerably for high-Z media.
leads to a reduction in the stopping power as will be shown although the magnitude of the correction is rather small (a few percent) for low atomic number media, but increases considerably for high-Z media.12.3.2 Effects of a Medium of Moving Electrons upon Stopping
To demonstrate the effects of moving target electrons upon the stopping power of an energetic charged particle, we first consider a simple case of a heavy charged particle traversing with velocity v a medium which we shall consider a case of free electrons uniformly distributed and with a common velocity v e (Sigmund 2006). This is a first attempt at modelling the interaction between an energetic charged particle and atomic electrons in which the latter are in motion; the effects of binding are neglected. Here, 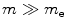 and, in the reference frame of the projectile which exists largely in the centre-of-mass, i the projectile would perceive itself as being bombarded by electrons with an incident velocity equal to
and, in the reference frame of the projectile which exists largely in the centre-of-mass, i the projectile would perceive itself as being bombarded by electrons with an incident velocity equal to
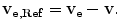
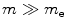 and, in the reference frame of the projectile which exists largely in the centre-of-mass, i the projectile would perceive itself as being bombarded by electrons with an incident velocity equal to
and, in the reference frame of the projectile which exists largely in the centre-of-mass, i the projectile would perceive itself as being bombarded by electrons with an incident velocity equal to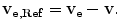
(12.7)
If the number density of the electrons is equal to 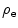 , then, with the assumptions and definitions above, the current density is uniform and equal to
, then, with the assumptions and definitions above, the current density is uniform and equal to
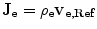
in units of  . Then the number of electrons scattered per unit time interval is equal to
. Then the number of electrons scattered per unit time interval is equal to
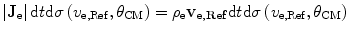
where the scattering angle 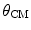 is measured within the scattering system’s centre-of-mass. Recall that we are operating within the projectile’s reference frame in which the electrons are considered to be the projectiles. Those electrons that are scattered by the ion through an angle
is measured within the scattering system’s centre-of-mass. Recall that we are operating within the projectile’s reference frame in which the electrons are considered to be the projectiles. Those electrons that are scattered by the ion through an angle 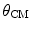 within the centre-of-mass will transfer a mean momentum to the projectile equal to
within the centre-of-mass will transfer a mean momentum to the projectile equal to
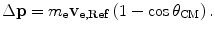
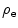 , then, with the assumptions and definitions above, the current density is uniform and equal to
, then, with the assumptions and definitions above, the current density is uniform and equal to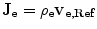
(12.8)
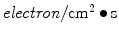 . Then the number of electrons scattered per unit time interval is equal to
. Then the number of electrons scattered per unit time interval is equal to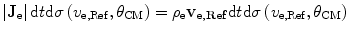
(12.9)
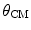 is measured within the scattering system’s centre-of-mass. Recall that we are operating within the projectile’s reference frame in which the electrons are considered to be the projectiles. Those electrons that are scattered by the ion through an angle
is measured within the scattering system’s centre-of-mass. Recall that we are operating within the projectile’s reference frame in which the electrons are considered to be the projectiles. Those electrons that are scattered by the ion through an angle 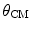 within the centre-of-mass will transfer a mean momentum to the projectile equal to
within the centre-of-mass will transfer a mean momentum to the projectile equal to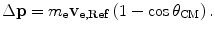
(12.10)
It is implicitly noted here that as a consequence of the uniformly moving and isotropic flux of electrons, the only non-zero component of the momentum transfer is that which is parallel to 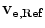 . The net force upon the ion as a consequence of these momentum transfers is simply the derivative of the momentum transfer or
. The net force upon the ion as a consequence of these momentum transfers is simply the derivative of the momentum transfer or
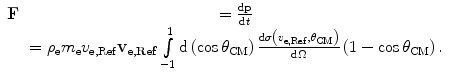
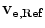 . The net force upon the ion as a consequence of these momentum transfers is simply the derivative of the momentum transfer or
. The net force upon the ion as a consequence of these momentum transfers is simply the derivative of the momentum transfer or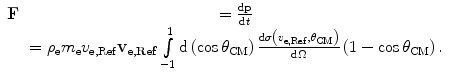
(12.11)
Now, in order to make the above description more analogous to that of atomic electrons, we extend from the case of incident electrons (in the centre-of-mass) with uniform velocities to that where the electrons exhibit a distribution of velocities, 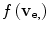 , as will be the case for the projection being incident to atomic electrons. In this case, the force of (12.11) is modified to the integral
, as will be the case for the projection being incident to atomic electrons. In this case, the force of (12.11) is modified to the integral
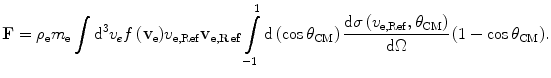
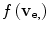 , as will be the case for the projection being incident to atomic electrons. In this case, the force of (12.11) is modified to the integral
, as will be the case for the projection being incident to atomic electrons. In this case, the force of (12.11) is modified to the integral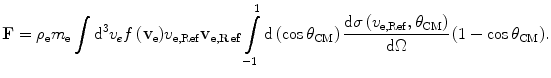
(12.12)
From (8.265), the energy lost per unit distance, or the linear stopping power, is
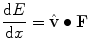
where 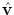 is the unit vector in the direction of the ion’s velocity. Then,
is the unit vector in the direction of the ion’s velocity. Then,
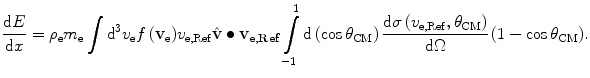
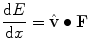
(12.13)
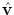 is the unit vector in the direction of the ion’s velocity. Then,
is the unit vector in the direction of the ion’s velocity. Then,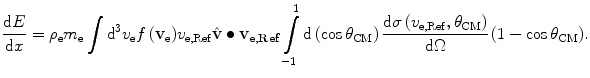
(12.14)
This can be rewritten in a simpler form through the application of the stopping cross section S of (8.85):
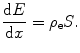
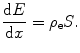
(12.15)
The stopping cross section per electron is
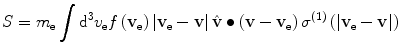
where the first-order transport cross section per electron is
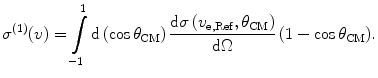
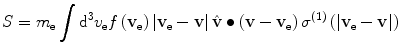
(12.16)
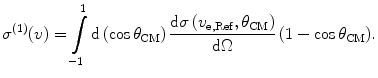
(12.17)
It can be seen how (12.17) is related to the first-order transport coefficient of the Goudsmit–Saunderson multiple Coulomb scatter theory given by (6.44).
If we consider the case of the ion velocity much greater than that of the electron, 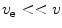 , then (12.16) reduces, and we can define
, then (12.16) reduces, and we can define
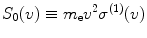
from which we can obtain the transport cross section per electron,
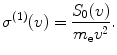
 , then (12.16) reduces, and we can define
, then (12.16) reduces, and we can define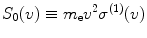
(12.18)
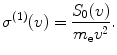
(12.19)
In order to evaluate this expression for the stopping cross section, we assume isotropicity in the velocity distribution (i.e. 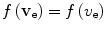 ) and then perform a Taylor expansion of
) and then perform a Taylor expansion of 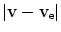 to second order in v e (whilst recalling that
to second order in v e (whilst recalling that 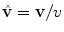 ) to give
) to give
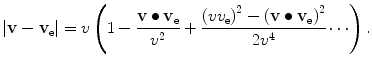
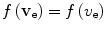 ) and then perform a Taylor expansion of
) and then perform a Taylor expansion of 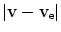 to second order in v e (whilst recalling that
to second order in v e (whilst recalling that 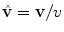 ) to give
) to give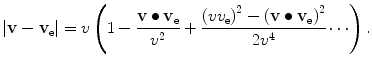
(12.21)
Applying this to (12.20) gives an expansion of the stopping cross section (Sigmund 1982) in the form
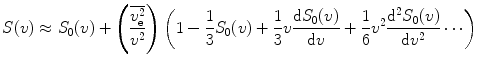
where the mean-square electron velocity is
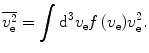
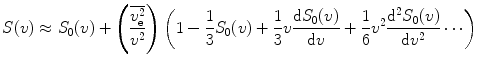
(12.22)
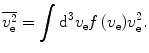
(12.23)
The stopping cross section result of (12.22) demonstrates that the orbital motion of the atomic electrons will introduce terms that will modify the stopping power which are of the order of 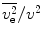 . That is, it predicts that the effect of atomic motion upon the stopping power is to reduce it and that this effect will increase with the atomic number of the medium (and, thus, increasing orbital velocity) and decrease with increasing projectile velocity. Binding has, however, been neglected. This effect is now considered within the context of the Bethe theory.
. That is, it predicts that the effect of atomic motion upon the stopping power is to reduce it and that this effect will increase with the atomic number of the medium (and, thus, increasing orbital velocity) and decrease with increasing projectile velocity. Binding has, however, been neglected. This effect is now considered within the context of the Bethe theory.
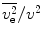 . That is, it predicts that the effect of atomic motion upon the stopping power is to reduce it and that this effect will increase with the atomic number of the medium (and, thus, increasing orbital velocity) and decrease with increasing projectile velocity. Binding has, however, been neglected. This effect is now considered within the context of the Bethe theory.
. That is, it predicts that the effect of atomic motion upon the stopping power is to reduce it and that this effect will increase with the atomic number of the medium (and, thus, increasing orbital velocity) and decrease with increasing projectile velocity. Binding has, however, been neglected. This effect is now considered within the context of the Bethe theory.12.3.3 Quantum-Mechanical Theory
The derivation of the Bethe soft-collision theory was based upon the first-order of the Born expansion. Thus, reflecting upon the results of Sect. 8.3.3 and assuming that the contributions of other perturbative effects (Bloch, Barkas–Andersen and density, as to be discussed later) can be neglected, we can write the correction to the stopping number due to shell corrections as
![$$ \begin{array}{cclcllclcl} \Delta L&= {L_{\mathrm{ Born}}}-{L_{00 }}\left( \beta \right) \\&= {L_{\mathrm{ Born}}} - \left[ { \ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}{\beta^2}} \right)- \ln \left( {1-{\beta^2}} \right)-{\beta^2}} \right]\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_12_Chapter_Equ001224.gif)
![$$ \begin{array}{cclcllclcl} \Delta L&= {L_{\mathrm{ Born}}}-{L_{00 }}\left( \beta \right) \\&= {L_{\mathrm{ Born}}} - \left[ { \ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}{\beta^2}} \right)- \ln \left( {1-{\beta^2}} \right)-{\beta^2}} \right]\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_12_Chapter_Equ001224.gif)
(12.24)
(Walske 1952; Sigmund 2006). In the nonrelativistic regime,
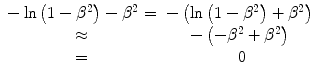
leaving us with a more commonly seen form
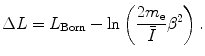
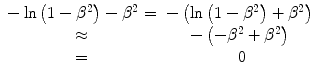
(12.25)
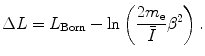
(12.26)
Recalling the definition of the logarithm of the mean excitation energy of (8.300) and splitting the integral of (12.27) at 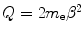 , we can rewrite (12.24) as
, we can rewrite (12.24) as
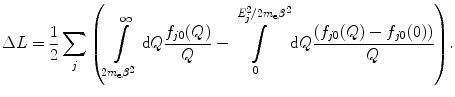
 , we can rewrite (12.24) as
, we can rewrite (12.24) as
(12.28)
This result follows as a consequence of the Thomas–Reiche–Kuhn rule (Appendix G.2.3) which gives
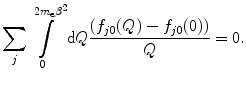
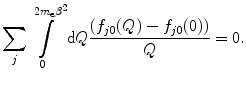
(12.29)
The result of (12.28) shows that the atomic electron motion correction 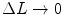 as the projectile velocity
as the projectile velocity 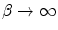 . While (12.28) has been evaluated numerically (Walske 1952, 1956; Khandelwal and Merzbacher 1966), an analytical form was derived by Fano (1963) for a one-electron atom:
. While (12.28) has been evaluated numerically (Walske 1952, 1956; Khandelwal and Merzbacher 1966), an analytical form was derived by Fano (1963) for a one-electron atom:
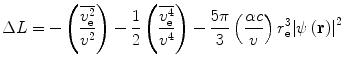
where 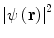 is the modulus squared of the electronic wavefunction.
is the modulus squared of the electronic wavefunction.
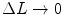 as the projectile velocity
as the projectile velocity  . While (12.28) has been evaluated numerically (Walske 1952, 1956; Khandelwal and Merzbacher 1966), an analytical form was derived by Fano (1963) for a one-electron atom:
. While (12.28) has been evaluated numerically (Walske 1952, 1956; Khandelwal and Merzbacher 1966), an analytical form was derived by Fano (1963) for a one-electron atom: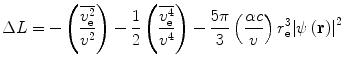
(12.30)
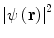 is the modulus squared of the electronic wavefunction.
is the modulus squared of the electronic wavefunction.12.3.4 The Atomic Shell Correction Factor, 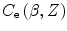
Consider a multi-electron atom with atomic number Z. We could write the change in stopping number due to orbital electron motion in the form
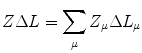
where the summation is over the atomic shells (e.g. 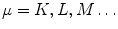 ),
), 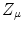 is the number of electrons in the μth shell and
is the number of electrons in the μth shell and 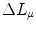 is the contribution of the electrons in that shell to the overall correction. As
is the contribution of the electrons in that shell to the overall correction. As 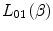 is a term which is added to the stopping number and reflects a negative quantity (reduction in collision stopping power), then, from (12.31), we write
is a term which is added to the stopping number and reflects a negative quantity (reduction in collision stopping power), then, from (12.31), we write
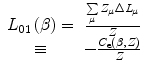
where 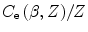 is a positive quantity known as the shell correction factor. From the above, we can also write the summation of the contributions over the atomic electron shells:
is a positive quantity known as the shell correction factor. From the above, we can also write the summation of the contributions over the atomic electron shells:
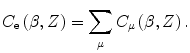
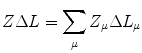
(12.31)
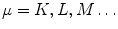 ),
), 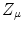 is the number of electrons in the μth shell and
is the number of electrons in the μth shell and 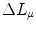 is the contribution of the electrons in that shell to the overall correction. As
is the contribution of the electrons in that shell to the overall correction. As 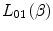 is a term which is added to the stopping number and reflects a negative quantity (reduction in collision stopping power), then, from (12.31), we write
is a term which is added to the stopping number and reflects a negative quantity (reduction in collision stopping power), then, from (12.31), we write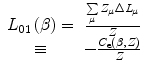
(12.32)
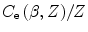 is a positive quantity known as the shell correction factor. From the above, we can also write the summation of the contributions over the atomic electron shells:
is a positive quantity known as the shell correction factor. From the above, we can also write the summation of the contributions over the atomic electron shells: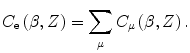
(12.33)
12.3.5 Parameterisation of 
In the Preface, we noted how the required accuracy of radiation absorbed dose assessment in therapeutic applications is demanding. As a consequence, even the small-magnitude effects of the atomic shell correction in low-Z media, such as tissue, must be accounted for accurately. In many numerical calculations (e.g. Monte Carlo) non-tabulated data are preferable to look-up tables. One useful application of this approach is the atomic shell correction factor. Barkas (1962) provided a useful semiempirical parameterisation of  :
:
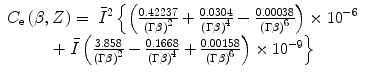
where the units of the mean excitation energy 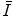 are eV.
are eV.  also contains the implicit Z-dependence of
also contains the implicit Z-dependence of 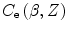 . The validity of this parameterisation of
. The validity of this parameterisation of 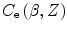 is limited to the product
is limited to the product ![$$ \gamma \beta > 0.13 $$
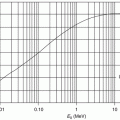
” src=”/wp-content/uploads/2016/04/A306762_1_En_12_Chapter_IEq001259.gif”></SPAN>. Figure <SPAN class=InternalRef><A href=]() 12.1 shows the shell correction term
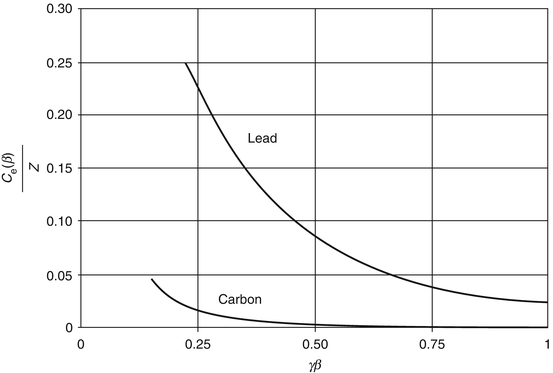
12.1 shows the shell correction term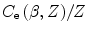 for protons in carbon and lead as functions of proton kinetic energy. The differences between the magnitudes of the correction factors with Z (atomic electron orbital velocity) and energy are clearly evident.
for protons in carbon and lead as functions of proton kinetic energy. The differences between the magnitudes of the correction factors with Z (atomic electron orbital velocity) and energy are clearly evident.
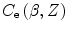 :
: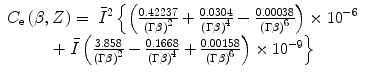
(12.34)
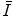 are eV.
are eV. 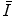 also contains the implicit Z-dependence of
also contains the implicit Z-dependence of 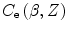 . The validity of this parameterisation of
. The validity of this parameterisation of 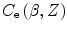 is limited to the product
is limited to the product 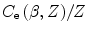 for protons in carbon and lead as functions of proton kinetic energy. The differences between the magnitudes of the correction factors with Z (atomic electron orbital velocity) and energy are clearly evident.
for protons in carbon and lead as functions of proton kinetic energy. The differences between the magnitudes of the correction factors with Z (atomic electron orbital velocity) and energy are clearly evident.
Fig. 12.1
Shell correction terms for carbon and lead as functions of γβ
12.4 Condensed Medium Term, 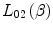
12.4.1 Introductory Comments
As noted earlier, the projectile’s electric field has been implicitly assumed to be in vacuo, and the medium through which it is travelling assumed to be a cold and dilute monoatomic gas (Halpern and Hall 1948; Fano 1956). Such simplifications ignore any response of a condensed medium to this moving electric field. Should the particle be travelling in a dense dielectric medium (such as tissue), atoms will be polarised, creating an array of electric dipoles which generate a secondary electric field limiting the particle’s electric field at a distance and reducing the stopping power. This effect is expected to be significant at high particle speeds, as shown by Fig. 8.2, where, as β → 1, the electric field parallel to the trajectory flattens and the orthogonal component extends such that the dielectric response of the medium will limit the relativistic rise in stopping power. Because the magnitude of this dielectric response is directly related to the number of secondary electric dipoles, it will clearly depend upon the medium’s physical density.2 This reduction in stopping power is characterised by the condensed medium term 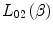 of the stopping number. It was Fermi who first recognised the need of a dielectric correction as the
of the stopping number. It was Fermi who first recognised the need of a dielectric correction as the 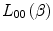 term of the stopping number goes to infinity due to the
term of the stopping number goes to infinity due to the 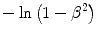 term as β → 1.
term as β → 1.
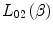 of the stopping number. It was Fermi who first recognised the need of a dielectric correction as the
of the stopping number. It was Fermi who first recognised the need of a dielectric correction as the 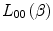 term of the stopping number goes to infinity due to the
term of the stopping number goes to infinity due to the 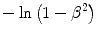 term as β → 1.
term as β → 1.We have already examined much of the effect of a condensed medium upon the stopping power of an energetic charged particle in our investigation of the Fermi theory of soft-collision energy loss provided earlier in Sect. 8.2.9. We will extend our results of that section and use the semi-classical work of Fermi (1940) to guide this derivation.
12.4.2 Electronic Polarisation
We begin first with a medium not much different from that we have considered to this point. We shall treat it is an isotropic monoatomic gas with interatomic distances sufficiently large that an atom can be treated in isolation.
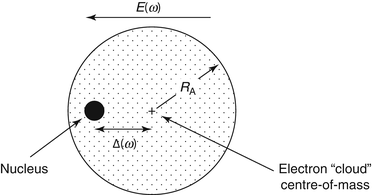
The atom is considered to consist of a negatively charged and mobile spherical electron cloud of charge −Ze and mass Zm e which, in its unperturbed state, is centred on a fixed nucleus of charge Ze. As a charged particle in motion passes by the atom, it will perturb the position of this electron cloud, leading to the polarisation of the atom, as demonstrated in Fig. 12.2. At high particle speeds, the shortness of the time duration of the electric field ‘pulse’ experienced by the atom, as shown in Fig. 8.2, will be dominated by high-frequency components, and in frequency space, one can consider the atom as being exposed to a high-frequency electric field. The displacement of the electron cloud, Δ, will be limited by the short duration of the pulse, and one can thus effectively ignore the spatial variation of the field over the atom as a result (in analogy to the result of (8.92)). The electron cloud will also experience a restorative force due to the mutual attraction between it and the nucleus and thus go into oscillatory motion. The attractive force can be calculated by modelling the electron cloud as a uniformly charged sphere of radius R A with an electric charge density, 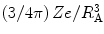 . The radial electric field due to this charge at a distance Δ from the centre of the atom is found by applying Gauss’ law to the sphere of radius Δ:
. The radial electric field due to this charge at a distance Δ from the centre of the atom is found by applying Gauss’ law to the sphere of radius Δ:
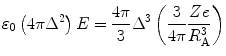 from which one obtains an expression for the magnitude of the electric field in terms of the displacement of the atomic electron cloud,
from which one obtains an expression for the magnitude of the electric field in terms of the displacement of the atomic electron cloud,
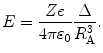
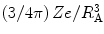 . The radial electric field due to this charge at a distance Δ from the centre of the atom is found by applying Gauss’ law to the sphere of radius Δ:
. The radial electric field due to this charge at a distance Δ from the centre of the atom is found by applying Gauss’ law to the sphere of radius Δ:
Fig. 12.2
Electronic polarisation due to an external electric field
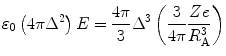
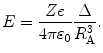
(12.35)
The restorative force acting upon the displaced electron cloud is 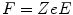 or
or
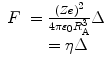
where we have defined the quantity 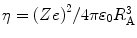 for later ease in display. This leads to
for later ease in display. This leads to
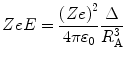 from which the magnitude of the product of the charge and its displacement, electric dipole moment, is
from which the magnitude of the product of the charge and its displacement, electric dipole moment, is
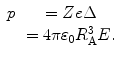
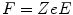 or
or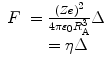
(12.36)
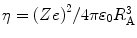 for later ease in display. This leads to
for later ease in display. This leads to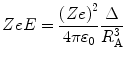
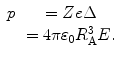
(12.37)
By describing the electric dipole moment as a vector, we can write
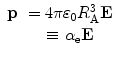
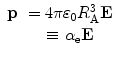
(12.38)
where 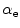 is defined as the electronic polarisability. It can be noted that the magnitude of the ratio of the electronic polarisability to the permittivity of free space,
is defined as the electronic polarisability. It can be noted that the magnitude of the ratio of the electronic polarisability to the permittivity of free space, 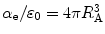 , is equal to the atomic volume.
, is equal to the atomic volume.
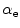 is defined as the electronic polarisability. It can be noted that the magnitude of the ratio of the electronic polarisability to the permittivity of free space,
is defined as the electronic polarisability. It can be noted that the magnitude of the ratio of the electronic polarisability to the permittivity of free space, 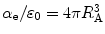 , is equal to the atomic volume.
, is equal to the atomic volume.Much like the previous analysis of the simple harmonic oscillator model of a single electron in our derivation of the dipole approximation in Sect. 8.2.4




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



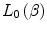
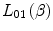
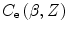
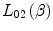
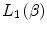
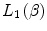
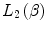
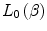
![$$ {L_{00 }}\left( \beta \right)=\left[ { \ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}{\beta^2}} \right)- \ln \left( {1-{\beta^2}} \right)-{\beta^2}} \right]. $$](/wp-content/uploads/2016/04/A306762_1_En_12_Chapter_Equ00124.gif)