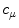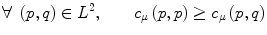-connectedness) and the related growing mechanism, it allows a strict and very simple integration between the analysis of topological connectedness and grey level similarities of the pixels belonging to the same region. By overcoming the previous drawback due to the need of some seed points selection, an iterative processing is here developed, able to adapt to the image content. The automatic selection of seed points is driven by intermediate connectedness results which alternates the analysis of inter-region similarities with inter-region separation measurements. The robustness of the method with respect to the three required parameters is discussed. Example cases related to real application domains are here presented and discussed.
Keywords
SegmentationFuzzy processingConnectednessMS lesion detection1 Introduction
For many years, image segmentation, or rather the process of identifying regions of interest starting from a digital image or volume, has been a major problem in image processing and a subject of extensive research work. Segmentation purpose is to partition an image into regions with homogeneous properties that faithfully correspond to the objects or parts of the objects of interest [5]. Among the methods and solutions suggested in the literature, the ones exploiting fuzzy logic have proved to be very promising. In fact, fuzziness is an inherent feature of real images, which are created through imaging devices and are naturally affected by defects, such as resolution limitations, blurring, noise, etc. Another hindrance to image analysis is the heterogeneity of the materials of the objects under examination, as occurs in the Biomedical and Remote Sensing fields, where it is necessary to observe the internal organs of living beings or to observe the Earth’s surface. Even when acquired from a single class, the imaging signal may be characterized by various levels of intensity. Fuzzy logic has been widely used in image segmentation, mainly to cluster the signal based on punctual features. Although the spatial and topological properties of images are important, only a few methods are able to exploit such an additional dimension [18]. In this context, fuzzy connectedness [8] may help to solve these problems identifying precisely the elements composing an image and belonging to the same region of interest, despite the existing uncertainties and variations in the original signal intensity levels. The aim of the proposed work is to extend the multi seed segmentation (MSMC) method proposed in Angiati et al. [1] for a fully automatic processing, thus achieving the so-called “Automatic Fuzzy Segmentation (AFS)” method. The core of the method is the fuzzy intensity-connectedness approach [8], here applied starting from a number of seed points which are automatically selected with the goal of the global image segmentation. This new method implements an iterative procedure which starts from a random selection of a few seed points, and stops with the complete segmentation of the image. Each iterative step alternates addition of new significant seeds and deletion of useless ones. This is a random process based on fuzzy operators, it is unsupervised and is only driven by the original data and intermediate results. It makes use of only three parameters and robustness can be easily proved, as reported in the evaluation session. The extensive experimental session has also proved good performances, when compared with other methods. The outline of the chapter is as follows. In Sect. 2, we shall briefly review the main segmentation approaches that are related to our method. Then the formulation of the proposed automatic segmentation method is presented. In Results section the applications of AFS will be reported and compared with already published methods. The conclusions section ends the chapter.
2 Proposed Method
Even though the spatial and topological properties of images are of major importance, they are only partially exploited by literature methods. A few approaches have been developed able to exploit the topological information in a fuzzy-logic framework [8, 17]. They are based on a close examination of the connectedness between pairs of image pixels and the relevant paths, in addition to the actual signal intensity. In Saha and Udupa [14] the so-called “relative fuzzy connectedness” method has been proposed where various objects in the image “are let to compete among themselves in having pixels as their members”. In the experiments there proposed, some seeds are utilized to specify a class of objects and some others correspond to different co-objects in the background. In the present work, starting from the fuzzy intensity-connectedness concept and the related computational method, Dellepiane et al. [8], new image processing steps are defined and introduced to realize an automatic unsupervised fuzzy image segmentation.
The proposed Automatic Fuzzy Segmentation (AFS) method represents an innovative extension of the system proposed in Angiati et al. [1] where a multi-region fuzzy seed-based segmentation has been described, devoted to the global segmentation of a given image.
Notation
Let an n-dimensional Euclidean space 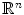 be subdivided into hypercubes called spels (an abbreviation for “space elements”). When
be subdivided into hypercubes called spels (an abbreviation for “space elements”). When 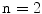 , spels are called pixels and they are represented by
, spels are called pixels and they are represented by 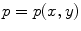 . When
. When 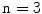 spels are called voxels and they are represented by
spels are called voxels and they are represented by 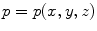 . Let L be an n-dimensional lattice of size
. Let L be an n-dimensional lattice of size 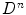 , made of the
, made of the 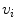 ‘s, with
‘s, with 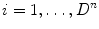 . An original digital image (or volume) is the field
. An original digital image (or volume) is the field
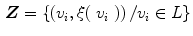
whose values range from 0 to the maximum grey-level, defined on the n-D lattice L. A fuzzy field M is a fuzzy subset defined in the following [13]:
![$$\begin{aligned} {{\varvec{M}}} = \left\{ {\left( {v_{i} ,\mu \left( {v_{i} }\right) } \right) /v_{i} \in L} \right\} \qquad \mu \in \left[ {0,1} \right] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ2.gif)
In fact, every digital picture/volume can be represented by an equivalent fuzzy field since, as stated in [6], there always exists a rational value r such that, for each spel 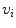 , we can write:
, we can write:
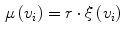
As it is well known, the purpose of image segmentation is the partition of an image M into a set of regions, 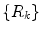 where each
where each 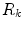 is a connected component and it holds that:
is a connected component and it holds that:
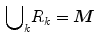
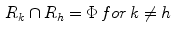
The automatic segmentation method here proposed is based on five steps that are iterated until the stop condition is verified. They are introduced in the following and will be described in detail in the next sections.
 be subdivided into hypercubes called spels (an abbreviation for “space elements”). When
be subdivided into hypercubes called spels (an abbreviation for “space elements”). When  , spels are called pixels and they are represented by
, spels are called pixels and they are represented by 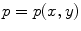 . When
. When 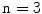 spels are called voxels and they are represented by
spels are called voxels and they are represented by 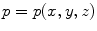 . Let L be an n-dimensional lattice of size
. Let L be an n-dimensional lattice of size 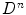 , made of the
, made of the 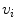 ‘s, with
‘s, with 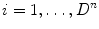 . An original digital image (or volume) is the field
. An original digital image (or volume) is the field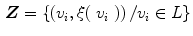
(1)
![$$\begin{aligned} {{\varvec{M}}} = \left\{ {\left( {v_{i} ,\mu \left( {v_{i} }\right) } \right) /v_{i} \in L} \right\} \qquad \mu \in \left[ {0,1} \right] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ2.gif)
(2)
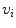 , we can write:
, we can write: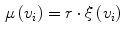
(3)
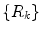 where each
where each 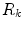 is a connected component and it holds that:
is a connected component and it holds that: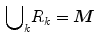
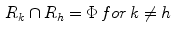
(4)
I. Fuzzy 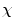 -connectedness Map Computation: A fuzzy
-connectedness Map Computation: A fuzzy 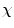 -connectedness map is independently computed for each selected seed. Unlike the method described in [1] where seeds are manually located by the user, in this method the seed points are automatically placed during the processing, in an adaptive way with respect to the actual image content.
-connectedness map is independently computed for each selected seed. Unlike the method described in [1] where seeds are manually located by the user, in this method the seed points are automatically placed during the processing, in an adaptive way with respect to the actual image content.
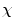 -connectedness Map Computation: A fuzzy
-connectedness Map Computation: A fuzzy 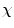 -connectedness map is independently computed for each selected seed. Unlike the method described in [1] where seeds are manually located by the user, in this method the seed points are automatically placed during the processing, in an adaptive way with respect to the actual image content.
-connectedness map is independently computed for each selected seed. Unlike the method described in [1] where seeds are manually located by the user, in this method the seed points are automatically placed during the processing, in an adaptive way with respect to the actual image content.II. Redundant Seeds Reduction: This step detects and obviates the situation where more than one seed is representing the same region.
III. Total Connectedness Map Computation: The seeds-related membership maps are merged into a single “Total-connectedness map” that is used to drive the next processing steps.
IV. Residual Detection and Seed Generation: It automatically finds new seeds when the previously selected ones are not sufficient to achieve a complete segmentation result.
V. Stopping Criterion and Labeling : appropriate stopping criterion and the labeling step are defined in subsection V.
The first iteration starts from a set of seed points randomly selected.
2.1 Fuzzy 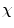 -connectedness Map Computation
-connectedness Map Computation
Before talking about 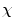 -connectedness we introduce the classical Fuzzy Connectedness concept. Given the generic fuzzy field M described in Eq. (2), we define the path
-connectedness we introduce the classical Fuzzy Connectedness concept. Given the generic fuzzy field M described in Eq. (2), we define the path 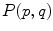 as a connected sequence of spels
as a connected sequence of spels 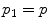 to a spel
to a spel 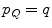 , where Q is the length of the path that joins the point p to the point q. We can express the conventional fuzzy degree of connectedness from p to q as in [12], that is:
, where Q is the length of the path that joins the point p to the point q. We can express the conventional fuzzy degree of connectedness from p to q as in [12], that is:
![$$\begin{aligned} c_{\mu } \left( {p,q} \right) = conn\left( {\mu ,p,q} \right) = \mathrm{max }_{{P(p,q)}} [\mathrm{min }_{{z \in P(p,q)}} \mu _{z} ] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ5.gif)
where the max is applied to all paths 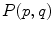 from p to q (thus referring to the optimum path connecting p with q), and the minimum is applied to all points z along the optimum path.
from p to q (thus referring to the optimum path connecting p with q), and the minimum is applied to all points z along the optimum path.
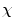 -connectedness we introduce the classical Fuzzy Connectedness concept. Given the generic fuzzy field M described in Eq. (2), we define the path
-connectedness we introduce the classical Fuzzy Connectedness concept. Given the generic fuzzy field M described in Eq. (2), we define the path 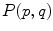 as a connected sequence of spels
as a connected sequence of spels 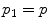 to a spel
to a spel 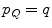 , where Q is the length of the path that joins the point p to the point q. We can express the conventional fuzzy degree of connectedness from p to q as in [12], that is:
, where Q is the length of the path that joins the point p to the point q. We can express the conventional fuzzy degree of connectedness from p to q as in [12], that is:![$$\begin{aligned} c_{\mu } \left( {p,q} \right) = conn\left( {\mu ,p,q} \right) = \mathrm{max }_{{P(p,q)}} [\mathrm{min }_{{z \in P(p,q)}} \mu _{z} ] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ5.gif)
(5)
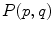 from p to q (thus referring to the optimum path connecting p with q), and the minimum is applied to all points z along the optimum path.
from p to q (thus referring to the optimum path connecting p with q), and the minimum is applied to all points z along the optimum path.This definition implies the following properties [3]:
From the above definition, it follows that a fuzzy connected component associated with a generic point q is a fuzzy subset that can be expressed as:
![$$\begin{aligned} \forall ~ {p}\in {{L}},~{\Gamma _{\upmu }^{q}} \left( {p} \right) = \mathrm{{max}}_{{P_{{(q,p)}} }} \left[ {min_{{z \in P_{{\left( {q,p} \right) }} }} \mu (z)} \right] = c_{\mu } \left( {q,p} \right) \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ6.gif)
For each spel p, its degree of connectedness to q in M is obtained as its membership in 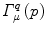 . In other words, a fuzzy connected component (in terms of grey-level homogeneity and topologic connectedness) can be identified for each image point. This approach is very similar to the segmentation process for some object, provided that a point q belonging to the object is selected. However, the objects of interest in a real image neither are always characterized by light or dark areas (tops or bottoms), nor they correspond to image plateaux, nor they are necessarily surrounded by high contrast background areas. The above definition of degree of connectedness does not take into account these considerations. Therefore, it is necessary to make the connectedness value independent of the reference grey-level. Moreover, it is worth noting that the classical
. In other words, a fuzzy connected component (in terms of grey-level homogeneity and topologic connectedness) can be identified for each image point. This approach is very similar to the segmentation process for some object, provided that a point q belonging to the object is selected. However, the objects of interest in a real image neither are always characterized by light or dark areas (tops or bottoms), nor they correspond to image plateaux, nor they are necessarily surrounded by high contrast background areas. The above definition of degree of connectedness does not take into account these considerations. Therefore, it is necessary to make the connectedness value independent of the reference grey-level. Moreover, it is worth noting that the classical 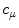 is not equivalent for both a signal and its complement, as differences are considered in an absolute way, not in a relative one.
is not equivalent for both a signal and its complement, as differences are considered in an absolute way, not in a relative one. 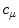 follows the behaviour of the field M for decreasing
follows the behaviour of the field M for decreasing 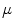 values, whereas it is independent of increasing
values, whereas it is independent of increasing 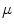 values. In the context of digital images this fact is a limitation, but it can be faced by using the definition of
values. In the context of digital images this fact is a limitation, but it can be faced by using the definition of 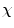 -connectivity, introduced in Dellepiane and Fontana [7]. In order to exploit the definition of connectedness for the purpose of image segmentation, we consider a modified field (with respect to a generic reference spel a, in the following referred to as a seed point) expressed as:
-connectivity, introduced in Dellepiane and Fontana [7]. In order to exploit the definition of connectedness for the purpose of image segmentation, we consider a modified field (with respect to a generic reference spel a, in the following referred to as a seed point) expressed as:
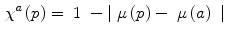
The 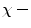 connectedness associated with the seed spel a can therefore be determined by applying Eq. (5) to the field
connectedness associated with the seed spel a can therefore be determined by applying Eq. (5) to the field
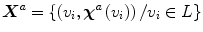 It takes the name of intensity connectedness or
It takes the name of intensity connectedness or 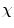 -connectedness and turns to be:
-connectedness and turns to be:
![$$\begin{aligned} c_{\chi ^{{a}}} \left( p \right) = conn\left( {{{\varvec{\chi }}^{{a}}}} ,a,p \right) = {max }_{{P(a,p)}} [{min }_{{z \in P(a,p)}} {{{\varvec{\chi }}^{{a}}}} (z)] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ8.gif)
It can easily be shown that this is equivalent to computing:
![$$\begin{aligned} c_{\chi ^{a}} \left( p \right) = 1 - \mathrm{min }_{{P\left( {a,p} \right) }} [ \mathrm{max }_{{z \in P\left( {a,p} \right) }} |{\mu }\left( z \right) - {\mu }\left( a \right) \,\,|] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ9.gif)
For a generic spel at any intensity level equal to 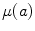 , the formula corresponds to the shiftment the signal
, the formula corresponds to the shiftment the signal 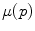 to
to 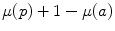 and, simultaneously, to the reverse of
and, simultaneously, to the reverse of 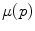 with respect to
with respect to 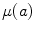 for each point with
for each point with ![$$\mu (p)>\mu (a)$$” src=”/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_IEq38.gif”></SPAN>.</DIV><br />
<DIV class=Para>Let <SPAN id=IEq39 class=InlineEquation><IMG alt=$$p(a,v_{i})$$ src=]() be a connected sequence of spels from a to the generic
be a connected sequence of spels from a to the generic 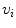 given by
given by 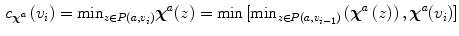
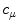 is symmetrical, i.e.,
is symmetrical, i.e.,
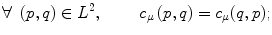
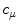 is transitive, i.e.,
is transitive, i.e.,
![$$ \forall ~\left( {p,q} \right) \in {{L}}^{2}, \qquad c_{\mu } \left( {p,q} \right) \ge ~\mathrm{{max}}_{{P_{{(q,p)}} }} \left[ {\mathrm{{min}}(c_{\mu } \left( {p,x} \right) ,c_{\mu } (x,q))} \right] $$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ21.gif)
![$$\begin{aligned} \forall ~ {p}\in {{L}},~{\Gamma _{\upmu }^{q}} \left( {p} \right) = \mathrm{{max}}_{{P_{{(q,p)}} }} \left[ {min_{{z \in P_{{\left( {q,p} \right) }} }} \mu (z)} \right] = c_{\mu } \left( {q,p} \right) \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ6.gif)
(6)
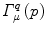 . In other words, a fuzzy connected component (in terms of grey-level homogeneity and topologic connectedness) can be identified for each image point. This approach is very similar to the segmentation process for some object, provided that a point q belonging to the object is selected. However, the objects of interest in a real image neither are always characterized by light or dark areas (tops or bottoms), nor they correspond to image plateaux, nor they are necessarily surrounded by high contrast background areas. The above definition of degree of connectedness does not take into account these considerations. Therefore, it is necessary to make the connectedness value independent of the reference grey-level. Moreover, it is worth noting that the classical
. In other words, a fuzzy connected component (in terms of grey-level homogeneity and topologic connectedness) can be identified for each image point. This approach is very similar to the segmentation process for some object, provided that a point q belonging to the object is selected. However, the objects of interest in a real image neither are always characterized by light or dark areas (tops or bottoms), nor they correspond to image plateaux, nor they are necessarily surrounded by high contrast background areas. The above definition of degree of connectedness does not take into account these considerations. Therefore, it is necessary to make the connectedness value independent of the reference grey-level. Moreover, it is worth noting that the classical 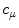 is not equivalent for both a signal and its complement, as differences are considered in an absolute way, not in a relative one.
is not equivalent for both a signal and its complement, as differences are considered in an absolute way, not in a relative one. 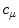 follows the behaviour of the field M for decreasing
follows the behaviour of the field M for decreasing 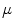 values, whereas it is independent of increasing
values, whereas it is independent of increasing 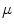 values. In the context of digital images this fact is a limitation, but it can be faced by using the definition of
values. In the context of digital images this fact is a limitation, but it can be faced by using the definition of 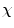 -connectivity, introduced in Dellepiane and Fontana [7]. In order to exploit the definition of connectedness for the purpose of image segmentation, we consider a modified field (with respect to a generic reference spel a, in the following referred to as a seed point) expressed as:
-connectivity, introduced in Dellepiane and Fontana [7]. In order to exploit the definition of connectedness for the purpose of image segmentation, we consider a modified field (with respect to a generic reference spel a, in the following referred to as a seed point) expressed as: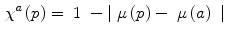
(7)
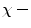 connectedness associated with the seed spel a can therefore be determined by applying Eq. (5) to the field
connectedness associated with the seed spel a can therefore be determined by applying Eq. (5) to the field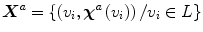
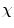 -connectedness and turns to be:
-connectedness and turns to be:![$$\begin{aligned} c_{\chi ^{{a}}} \left( p \right) = conn\left( {{{\varvec{\chi }}^{{a}}}} ,a,p \right) = {max }_{{P(a,p)}} [{min }_{{z \in P(a,p)}} {{{\varvec{\chi }}^{{a}}}} (z)] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ8.gif)
(8)
![$$\begin{aligned} c_{\chi ^{a}} \left( p \right) = 1 - \mathrm{min }_{{P\left( {a,p} \right) }} [ \mathrm{max }_{{z \in P\left( {a,p} \right) }} |{\mu }\left( z \right) - {\mu }\left( a \right) \,\,|] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ9.gif)
(9)
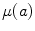 , the formula corresponds to the shiftment the signal
, the formula corresponds to the shiftment the signal 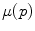 to
to 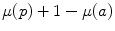 and, simultaneously, to the reverse of
and, simultaneously, to the reverse of 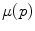 with respect to
with respect to 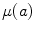 for each point with
for each point with 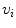 given by
given by 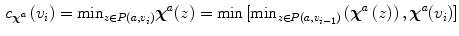
(10)
![$$\begin{aligned} c_{{{\varvec{\chi }}}^{a}} \left( {v_{i} } \right) = \mathrm{min } \, [{c}_{{{\varvec{\chi }}}^{a}} \left( {v_{{i - 1}} } \right) ,{\varvec{\chi }}^{{a}} (v_{i} )] \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ11.gif)
(11)
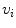 is equal to its value in
is equal to its value in 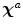 or, if its
or, if its 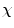 -connectedness has not the minimum value in that path, to the intensity connectedness of the previous spel along the best path from a to
-connectedness has not the minimum value in that path, to the intensity connectedness of the previous spel along the best path from a to 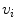 .
.2.2 Redundant Seeds Reduction
At the beginning, the seed points are randomly placed, then it is required to determine the eventual cases where more than one seed is associated to the same region, before calculating the total map. It is thus necessary to define and search these situations, in order to collapse more seeds into one. To this aim, we define the so-called “redundant seeds”. To find the redundant seeds, a distance between the connectivity map generated from seed a and the one generated from seed b is computed:
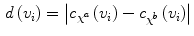
associated to the distance energy value:
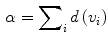
A decreasing sigmoidal fuzzy membership function “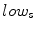 ”, with flex point in s, is also defined:
”, with flex point in s, is also defined:
![$$\begin{aligned} low_{s} : \rightarrow \left[ {0,1} \right] ~\left\{ {\begin{array}{c} {\mathrm{lim }_{{\alpha \rightarrow 0}}\, { low}_{s} = 1} \\ {\mathrm{lim }_{{\alpha \rightarrow 1}}\, { low}_{s} = 0} \\ \end{array}} \right. \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ14.gif)
In such a way, two seeds a and b are considered to be redundant if the energy of the distance field is low, given that the original grey level of the two seeds are similar enough. Thanks to the second constraint, only (T-1) comparisons are required at each iteration, starting from a list where seeds are ordered on the basis of their original grey level, being T the actual number of seed points.
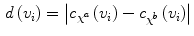
(12)
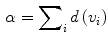
(13)
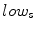 ”, with flex point in s, is also defined:
”, with flex point in s, is also defined:![$$\begin{aligned} low_{s} : \rightarrow \left[ {0,1} \right] ~\left\{ {\begin{array}{c} {\mathrm{lim }_{{\alpha \rightarrow 0}}\, { low}_{s} = 1} \\ {\mathrm{lim }_{{\alpha \rightarrow 1}}\, { low}_{s} = 0} \\ \end{array}} \right. \end{aligned}$$](/wp-content/uploads/2016/03/A320009_1_En_4_Chapter_Equ14.gif)
(14)
2.3 Total Connectedness Map
Let 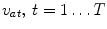 be T random seed-points, each corresponds to a different class or region. The Multi-Seed Multi-Class (MSMC) method allows to separately identify a region associated to a seed. For each seed point
be T random seed-points, each corresponds to a different class or region. The Multi-Seed Multi-Class (MSMC) method allows to separately identify a region associated to a seed. For each seed point 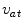 , the corresponding intensity-connectedness field
, the corresponding intensity-connectedness field 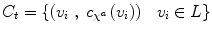 is generated. To this end, for each intensity-connectedness map a parallel processing is executed, by running the growing mechanism starting from each seed
is generated. To this end, for each intensity-connectedness map a parallel processing is executed, by running the growing mechanism starting from each seed 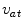 , independently to each other. In this way, each intensity-connectedness field
, independently to each other. In this way, each intensity-connectedness field 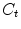 separately contains information about the region/object corresponding to the related seed point. The computation of all the membership values assigned to a spel is equivalent to the generation of a hyper-matrix similar to the c-fuzzy-partition matrix defined in Bezdek [2]. A single final-intensity-connectedness-map field,
separately contains information about the region/object corresponding to the related seed point. The computation of all the membership values assigned to a spel is equivalent to the generation of a hyper-matrix similar to the c-fuzzy-partition matrix defined in Bezdek [2]. A single final-intensity-connectedness-map field, 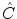 , integrating information derived from all the seeds, is generated by applying the fuzzy union:
, integrating information derived from all the seeds, is generated by applying the fuzzy union:
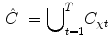
where
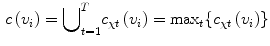
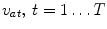 be T random seed-points, each corresponds to a different class or region. The Multi-Seed Multi-Class (MSMC) method allows to separately identify a region associated to a seed. For each seed point
be T random seed-points, each corresponds to a different class or region. The Multi-Seed Multi-Class (MSMC) method allows to separately identify a region associated to a seed. For each seed point 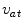 , the corresponding intensity-connectedness field
, the corresponding intensity-connectedness field 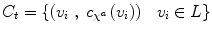 is generated. To this end, for each intensity-connectedness map a parallel processing is executed, by running the growing mechanism starting from each seed
is generated. To this end, for each intensity-connectedness map a parallel processing is executed, by running the growing mechanism starting from each seed 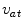 , independently to each other. In this way, each intensity-connectedness field
, independently to each other. In this way, each intensity-connectedness field 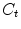 separately contains information about the region/object corresponding to the related seed point. The computation of all the membership values assigned to a spel is equivalent to the generation of a hyper-matrix similar to the c-fuzzy-partition matrix defined in Bezdek [2]. A single final-intensity-connectedness-map field,
separately contains information about the region/object corresponding to the related seed point. The computation of all the membership values assigned to a spel is equivalent to the generation of a hyper-matrix similar to the c-fuzzy-partition matrix defined in Bezdek [2]. A single final-intensity-connectedness-map field, 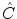 , integrating information derived from all the seeds, is generated by applying the fuzzy union:
, integrating information derived from all the seeds, is generated by applying the fuzzy union: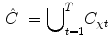
(15)
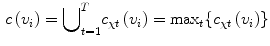
(16)
2.4 Residual Detection and Seed Generation
2.4.1 Residuals’ Map Calculation
When a significant region is not located by any of the selected seeds, a new seed point must be appropriately looked for. Once it is found it is added to the already existing seeds list and the related 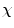 -connectedness map is generated. To the end of such a new seed selection, the intermediate total connectedness map is used. In fact, when a region has not been properly identified, some “residuals” appear in the map and can be automatically located. We here define “residuals” as those spels that have low values in the total-connectedness map, thus indicating that they are not appropriately represented by any of the selected seeds. The residual map, P, is then derived by assigning to each spel site the value:
-connectedness map is generated. To the end of such a new seed selection, the intermediate total connectedness map is used. In fact, when a region has not been properly identified, some “residuals” appear in the map and can be automatically located. We here define “residuals” as those spels that have low values in the total-connectedness map, thus indicating that they are not appropriately represented by any of the selected seeds. The residual map, P, is then derived by assigning to each spel site the value:
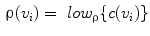
Since the location of new seed points is based on the residual map, a post-processing step devoted to its regularization is applied as explained in Sect 2.4.2.
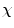 -connectedness map is generated. To the end of such a new seed selection, the intermediate total connectedness map is used. In fact, when a region has not been properly identified, some “residuals” appear in the map and can be automatically located. We here define “residuals” as those spels that have low values in the total-connectedness map, thus indicating that they are not appropriately represented by any of the selected seeds. The residual map, P, is then derived by assigning to each spel site the value:
-connectedness map is generated. To the end of such a new seed selection, the intermediate total connectedness map is used. In fact, when a region has not been properly identified, some “residuals” appear in the map and can be automatically located. We here define “residuals” as those spels that have low values in the total-connectedness map, thus indicating that they are not appropriately represented by any of the selected seeds. The residual map, P, is then derived by assigning to each spel site the value: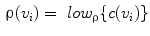
(17)
2.4.2 Residual Map Regularization and Seed Generation
Due to the complexity of the images at hand, the presence of noise, and the low contrast between regions, many spurious spels are usually detected in the residual map. For such reasons, and in order to avoid the selection of seeds related to too small regions, a regularization step is proposed before the new seed selection task. To this end, the erosion operator of Mathematical Morphology (also called Minkowski difference) is applied to the residual map. A 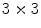 structuring element (SE) is used and is applied to the whole residual map. Erosion of the residual field P is defined in Shapiro and Stockman [16]. The so obtained
structuring element (SE) is used and is applied to the whole residual map. Erosion of the residual field P is defined in Shapiro and Stockman [16]. The so obtained 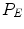 map has homogeneous bright areas from where we can extract the new seed points. These areas passing from P to
map has homogeneous bright areas from where we can extract the new seed points. These areas passing from P to 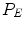 , are reduced in size, decreasing the number of spels corresponding to the potential seeds and improving the probability of placing a seed far from the region border. The new seeds are randomly placed inside the brightest areas of the eroded residual map
, are reduced in size, decreasing the number of spels corresponding to the potential seeds and improving the probability of placing a seed far from the region border. The new seeds are randomly placed inside the brightest areas of the eroded residual map 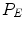 and the iterative process is repeated starting from the first step. The stopping condition is based on the disappearance of any residual.
and the iterative process is repeated starting from the first step. The stopping condition is based on the disappearance of any residual.
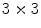 structuring element (SE) is used and is applied to the whole residual map. Erosion of the residual field P is defined in Shapiro and Stockman [16]. The so obtained
structuring element (SE) is used and is applied to the whole residual map. Erosion of the residual field P is defined in Shapiro and Stockman [16]. The so obtained 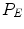 map has homogeneous bright areas from where we can extract the new seed points. These areas passing from P to
map has homogeneous bright areas from where we can extract the new seed points. These areas passing from P to 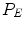 , are reduced in size, decreasing the number of spels corresponding to the potential seeds and improving the probability of placing a seed far from the region border. The new seeds are randomly placed inside the brightest areas of the eroded residual map
, are reduced in size, decreasing the number of spels corresponding to the potential seeds and improving the probability of placing a seed far from the region border. The new seeds are randomly placed inside the brightest areas of the eroded residual map 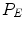 and the iterative process is repeated starting from the first step. The stopping condition is based on the disappearance of any residual.
and the iterative process is repeated starting from the first step. The stopping condition is based on the disappearance of any residual.2.5 Stopping Criterion and Labeling
2.5.1 Stop Condition
The stop condition 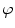 is essential because it determines when it is no longer necessary to find new seed points. Since the new seed points are searched directly on the eroded residuals’ map
is essential because it determines when it is no longer necessary to find new seed points. Since the new seed points are searched directly on the eroded residuals’ map 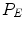 , just on this field
, just on this field 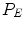 the stop condition is evaluated. Each time a residual is calculated and a new seed is determined (actually we may look for more seeds at a time), a new temporary connectivity map
the stop condition is evaluated. Each time a residual is calculated and a new seed is determined (actually we may look for more seeds at a time), a new temporary connectivity map 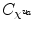 is calculated. Consequently, each time a new residuals’ map
is calculated. Consequently, each time a new residuals’ map 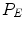 is calculated with its connectivity map
is calculated with its connectivity map 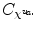 For each temporary residuals’ map
For each temporary residuals’ map 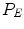 , the occurrence of bright spels on the whole image are calculated
, the occurrence of bright spels on the whole image are calculated 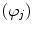 as the average map integral value. This is a percentage measure that will have a decreasing trend until it reaches a minimum value. The stop condition is then defined as the minimum percentage number,
as the average map integral value. This is a percentage measure that will have a decreasing trend until it reaches a minimum value. The stop condition is then defined as the minimum percentage number, 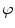




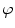 is essential because it determines when it is no longer necessary to find new seed points. Since the new seed points are searched directly on the eroded residuals’ map
is essential because it determines when it is no longer necessary to find new seed points. Since the new seed points are searched directly on the eroded residuals’ map 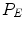 , just on this field
, just on this field 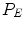 the stop condition is evaluated. Each time a residual is calculated and a new seed is determined (actually we may look for more seeds at a time), a new temporary connectivity map
the stop condition is evaluated. Each time a residual is calculated and a new seed is determined (actually we may look for more seeds at a time), a new temporary connectivity map 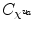 is calculated. Consequently, each time a new residuals’ map
is calculated. Consequently, each time a new residuals’ map 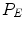 is calculated with its connectivity map
is calculated with its connectivity map 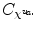 For each temporary residuals’ map
For each temporary residuals’ map 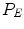 , the occurrence of bright spels on the whole image are calculated
, the occurrence of bright spels on the whole image are calculated 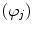 as the average map integral value. This is a percentage measure that will have a decreasing trend until it reaches a minimum value. The stop condition is then defined as the minimum percentage number,
as the average map integral value. This is a percentage measure that will have a decreasing trend until it reaches a minimum value. The stop condition is then defined as the minimum percentage number, 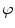
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree