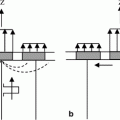
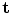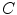Fig. 13.1
A pulse-echo testing setup where an array element acts as both a sending and receiving element in examining a flaw through an interface
![$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{c}}},\omega)=-2{{\rho }_{2}}{{c}_{\beta 2}}{{\omega }^{2}}\int_{{{S}_{\text{lit}}}}{\left\{ R_{23}^{\beta ;\beta }{{[ \tilde{U}_{\beta }^{(1)}({{\mathbf{x}}_{\text{c}}},\mathbf{x},\omega ) ]}^{2}}\exp [ 2\text{i}\omega \mathcal{T}( {{\mathbf{x}}_{\text{c}}},\mathbf{x} ) ]\text{d}S(\mathbf{x}) \right\}}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ1.gif)
(13.1)
We will replace the normalized displacement amplitude term 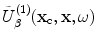 by the corresponding normalized velocity amplitude
by the corresponding normalized velocity amplitude 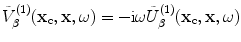 . Then Eq. (13.1) becomes
. Then Eq. (13.1) becomes
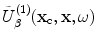 by the corresponding normalized velocity amplitude
by the corresponding normalized velocity amplitude 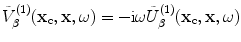 . Then Eq. (13.1) becomes
. Then Eq. (13.1) becomes![$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{c}}},\omega)=2{{\rho }_{2}}{{c}_{\beta 2}}\int_{{{S}_{\text{lit}}}}{\left\{ R_{23}^{\beta ;\beta }{{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{x},\omega) ]}^{2}}\exp [ 2\text{i}\omega {T}( {{\mathbf{x}}_{\text{c}}},\mathbf{x} ) ]\text{d}S(\mathbf{x}) \right\}}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ2.gif)
(13.2)
As done in Chap. 12 for 2-D scalar problems (see Eq. 12.16), we can define a singular function, 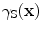 , of the lit surface which in 3-D problems has sampling property [1]:
, of the lit surface which in 3-D problems has sampling property [1]:
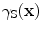 , of the lit surface which in 3-D problems has sampling property [1]:
, of the lit surface which in 3-D problems has sampling property [1]: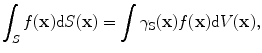
(13.3)
and also define the reflectivity of the surface as 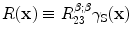 to turn the surface integral in Eq. (13.3) into a volume integral of that reflectivity over all space, i.e.
to turn the surface integral in Eq. (13.3) into a volume integral of that reflectivity over all space, i.e.
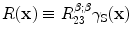 to turn the surface integral in Eq. (13.3) into a volume integral of that reflectivity over all space, i.e.
to turn the surface integral in Eq. (13.3) into a volume integral of that reflectivity over all space, i.e.![$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{c}}},\omega)=2{{\rho }_{2}}{{c}_{\beta 2}}\int{\left\{ {R}(\mathbf{x}){{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{x},\omega) ]}^{2}}\exp [ 2\text{i}\omega {T}( {{\mathbf{x}}_{\text{c}}},\mathbf{x} ) ]\text{d}V(\mathbf{x}) \right\}}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ4.gif)
(13.4)
We will now show how we can invert Eq. (13.4) to obtain an image of the flaw properties without making the small flaw assumption, as done in Chap. 12, following a similar approach to that of Bleistein et al. for scalar problems [2]. Specifically, we will again define that image, 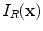 , to simply be the reflectivity of the flaw surface :
, to simply be the reflectivity of the flaw surface :
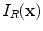 , to simply be the reflectivity of the flaw surface :
, to simply be the reflectivity of the flaw surface :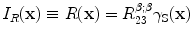
(13.5)
and obtain an expression for the image in terms of the measured values, 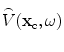 .
.
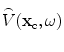 .
.In a real ultrasonic array, the values of 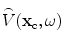 are only measured at the discrete locations of the array elements and at discretely sampled frequencies but in inverting Eq. (13.4) we will find it convenient to consider
are only measured at the discrete locations of the array elements and at discretely sampled frequencies but in inverting Eq. (13.4) we will find it convenient to consider 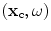 as continuous variables. We will also parameterize the array element locations,
as continuous variables. We will also parameterize the array element locations, 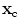 , assumed here to lie on a planar surface, in terms of two auxiliary variables
, assumed here to lie on a planar surface, in terms of two auxiliary variables 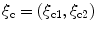 , i.e.
, i.e. 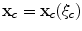 . Since Eq. (13.4) is in a form similar to that of a 3-D Fourier transform, we will seek to obtain the image of the flaw at a point
. Since Eq. (13.4) is in a form similar to that of a 3-D Fourier transform, we will seek to obtain the image of the flaw at a point 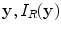 , to be in the form of a similar inverse Fourier-like transform given by
, to be in the form of a similar inverse Fourier-like transform given by
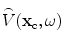 are only measured at the discrete locations of the array elements and at discretely sampled frequencies but in inverting Eq. (13.4) we will find it convenient to consider
are only measured at the discrete locations of the array elements and at discretely sampled frequencies but in inverting Eq. (13.4) we will find it convenient to consider 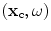 as continuous variables. We will also parameterize the array element locations,
as continuous variables. We will also parameterize the array element locations, 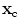 , assumed here to lie on a planar surface, in terms of two auxiliary variables
, assumed here to lie on a planar surface, in terms of two auxiliary variables 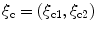 , i.e.
, i.e. 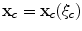 . Since Eq. (13.4) is in a form similar to that of a 3-D Fourier transform, we will seek to obtain the image of the flaw at a point
. Since Eq. (13.4) is in a form similar to that of a 3-D Fourier transform, we will seek to obtain the image of the flaw at a point 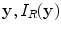 , to be in the form of a similar inverse Fourier-like transform given by
, to be in the form of a similar inverse Fourier-like transform given by![$$ {{{I}}_{R}}(\mathbf{y})=\int{\int{K( \mathbf{y},{{\mathbf{x}}_{\text{c}}},\omega)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{c}}},\omega)\exp [{-}2\text{i}\omega {T}( {{\mathbf{x}}_{\text{c}}},\mathbf{y} ) ]{{\text{d}}^{2}}{{\xi }_{\text{c}}}\text{d}\omega }}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ6.gif)
(13.6)
To see if this representation of the flaw image is possible and to obtain the unknown function 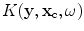 , we will place Eq. (13.4) into (13.6) to obtain
, we will place Eq. (13.4) into (13.6) to obtain
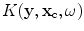 , we will place Eq. (13.4) into (13.6) to obtain
, we will place Eq. (13.4) into (13.6) to obtain![$${{I}_{R}}(\mathbf{y})=\int{\int{\int{2{{\rho }_{2}}{{c}_{\beta 2}}}K\left( \mathbf{y},{{\mathbf{x}}_{\text{c}}},\omega \right){{\left[ \tilde{V}_{\beta }^{(1)}\left( {{\mathbf{x}}_{\text{c}}},\mathbf{x},\omega \right) \right]}^{2}}}}\cdot \exp \left[ 2\text{i}\omega T\left( {{\mathbf{x}}_{\text{c}}},\mathbf{x} \right)-2\text{i}\omega T\left( {{\mathbf{x}}_{\text{c}}},\mathbf{y} \right) \right]{{\mathcal{I}}_{R}}(\mathbf{x}){{\text{d}}^{2}}{{\mathbf{\xi }}_{\text{c}}}\text{d}\omega\text{d}V(\mathbf{x}).$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ7.gif)
(13.7)
Since in Eq. (13.7) we are relating the flaw image to a volume integral over itself, then in some sense we must have
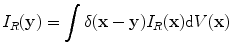
(13.8)
or equivalently, in some sense
![$$ \begin{matrix} \delta (\mathbf{x}-\mathbf{y})={{\int{\int{2{{\rho }_{2}}{{c}_{\beta 2}}K( \mathbf{y},{{\mathbf{x}}_{\text{c}}},\omega)[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{x},\omega) ]}}}^{2}}\\ \cdot \exp [ 2\text{i}\omega {T}( {{\mathbf{x}}_{\text{c}}},\mathbf{x} )-2\text{i}\omega {T}( {{\mathbf{x}}_{\text{c}}},\mathbf{y} ) ]{{\text{d}}^{2}}{{\mathbf{\xi }}_{\text{c}}}\text{d}\omega \\\end{matrix}, $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ9.gif)
(13.9)
where 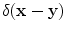 is the Dirac delta function. At least asymptotically at high frequencies Eq. (13.9) may be valid since at high frequencies the rapidly varying phase terms in the integrand will cause the integrals to be small except near the critical point
is the Dirac delta function. At least asymptotically at high frequencies Eq. (13.9) may be valid since at high frequencies the rapidly varying phase terms in the integrand will cause the integrals to be small except near the critical point 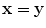 , where the phase term in Eq. (13.9) vanishes . Near this point, if we expand the phase term to first order and evaluate the amplitude at that point we have
, where the phase term in Eq. (13.9) vanishes . Near this point, if we expand the phase term to first order and evaluate the amplitude at that point we have
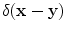 is the Dirac delta function. At least asymptotically at high frequencies Eq. (13.9) may be valid since at high frequencies the rapidly varying phase terms in the integrand will cause the integrals to be small except near the critical point
is the Dirac delta function. At least asymptotically at high frequencies Eq. (13.9) may be valid since at high frequencies the rapidly varying phase terms in the integrand will cause the integrals to be small except near the critical point 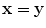 , where the phase term in Eq. (13.9) vanishes . Near this point, if we expand the phase term to first order and evaluate the amplitude at that point we have
, where the phase term in Eq. (13.9) vanishes . Near this point, if we expand the phase term to first order and evaluate the amplitude at that point we have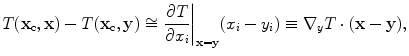
(13.10)
so that
![$$ \delta (\mathbf{x}-\mathbf{y})=\int{\int{2{{\rho }_{2}}{{c}_{\beta 2}}K( \mathbf{y},{{\mathbf{x}}_{\text{c}}},\omega){{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{y},\omega) ]}^{2}}}}\exp [ 2\text{i}\omega {{\nabla }_{y}}{T}\cdot (\mathbf{x}-\mathbf{y}) ]{{\text{d}}^{2}}{{\xi }_{\text{c}}}\text{d}\omega . $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ11.gif)
(13.11)
If we now define a wave number vector, 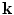 , as
, as
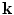 , as
, as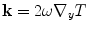
(13.12)
we can transform the integral in Eq. (13.11) into one over 3-D k-space, i.e.
![$$ \delta (\mathbf{x}-\mathbf{y})=\int{\int{2{{\rho }_{2}}{{c}_{\beta 2}}K( \mathbf{y},{{\mathbf{x}}_{\text{c}}},\omega){{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{y},\omega) ]}^{2}}\left| \frac{\partial ( \omega ,{{\xi }_{\text{c}1}},{{\xi }_{\text{c}2}} )}{\partial (\mathbf{k})} \right|}}\exp \text{ }\!\![\!\!\text{ i}\mathbf{k}\cdot (\mathbf{x}-\mathbf{y})]{{\text{d}}^{3}}\mathbf{k}, $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ13.gif)
(13.13)
where the inverse of the Jacobian of the transformation for this pulse-echo case can be written as
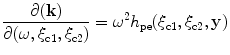
(13.14)
with
![$$\begin{aligned}{{h}_{\text{pe}}}( {{\xi}_{\text{c}1}},{{\xi}_{\text{c}2}},\mathbf{y} )=\det\left[\begin{array}{c} 2{{\nabla}_{y}}{T}\\ 2\tfrac{\partial}{\partial {{\xi}_{\text{c}1}}}( {{\nabla }_{y}}{T})\\2\tfrac{\partial }{\partial {{\xi }_{\text{c}2}}}({{\nabla}_{y}}{T} )\end{array}\right],\end{aligned} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ15.gif)
(13.15)
which is called the Beylkin determinant [2]. If we take
![$$ K( \mathbf{y},{{\mathbf{x}}_{\text{c}}},\omega)=\frac{1}{8{{\text{ }\!\!\pi\!\!\text{ }}^{3}}}\frac{{{\omega }^{2}}|{{h}_{\text{pe}}}( {{\xi }_{\text{c}1}},{{\xi }_{\text{c}2}},\mathbf{y} )|}{2{{\rho }_{2}}{{c}_{\beta 2}}{{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{y},\omega) ]}^{2}}} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ16.gif)
(13.16)
then Eq. (13.13) becomes
![$$ \delta (\mathbf{x}-\mathbf{y})=\frac{1}{8{{\text{ }\!\!\pi\!\!\text{ }}^{3}}}\int{\int{\exp \text{ }\!\![\!\!\text{ i}\mathbf{k}\cdot (\mathbf{x}-\mathbf{y})]{{\text{d}}^{3}}\mathbf{k}}}, $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ17.gif)
(13.17)
which is indeed just a k-space transform representation of the delta function. Thus, if we place Eq. (13.16) into (13.6) we now have an explicit expression for the image given by
![$${I}_{R}(\mathbf{y})=\frac{1}{16{{\text{ }\!\!\pi\!\!\text{ }}^{3}}{{\rho }_{2}}{{c}_{\beta 2}}}\int{\int{\frac{{{\omega}^{2}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}\left({{\mathbf{x}}_{\text{c}}},\omega \right)}{{{\left[\tilde{V}_{\beta }^{(1)}\left({{\mathbf{x}}_{\text{c}}},\mathbf{y},\omega \right)\right]}^{2}}}|{{h}_{\text{pe}}}\left( {{\xi }_{\text{c}1}},{{\xi}_{\text{c}2}},\mathbf{y} \right)|\exp \left[ -2\text{i}\omega{T}\left( {{\mathbf{x}}_{\text{c}}},\mathbf{y} \right)\right]{{\text{d}}^{2}}{{\xi }_{\text{c}}}\text{d}\omega }}.$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ18.gif)
(13.18)
The evaluation of the Beylkin determinant can be made particularly easy by choosing the 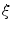 -parameters to be the spherical coordinates
-parameters to be the spherical coordinates 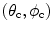 centered around a reference unit vector in the incident wave direction at point
centered around a reference unit vector in the incident wave direction at point 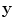 . Then, as shown in Appendix A, we have
. Then, as shown in Appendix A, we have
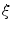 -parameters to be the spherical coordinates
-parameters to be the spherical coordinates 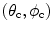 centered around a reference unit vector in the incident wave direction at point
centered around a reference unit vector in the incident wave direction at point 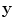 . Then, as shown in Appendix A, we have
. Then, as shown in Appendix A, we have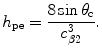
(13.19)
In this case
![$${I}_{R}(\mathbf{y})=\frac{1}{2{{\text{ }\!\!\pi\!\!\text{ }}^{3}}{{\rho }_{2}}c_{\beta 2}^{4}}\int{\int{\frac{{{\omega }^{2}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}\left( {{\mathbf{x}}_{\text{c}}},\omega \right)}{{{\left[ \tilde{V}_{\beta }^{(1)}\left( {{\mathbf{x}}_{\text{c}}},\mathbf{y},\omega \right) \right]}^{2}}}\exp \left[ -2\text{i}\omega {T}\left( {{\mathbf{x}}_{\text{c}}},\mathbf{y} \right) \right]\sin {{\theta }_{\text{c}}}\text{d}{{\theta }_{\text{c}}}\text{d}{{\phi }_{\text{c}}}\text{d}\omega }},$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ20.gif)
(13.20)
where 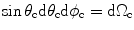 is just a differential solid angle as measured in these spherical coordinates. If we let
is just a differential solid angle as measured in these spherical coordinates. If we let 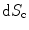 be a differential area element at the plane of the array we can transform the integration over the solid angle to an integration over the array element coordinates to find
be a differential area element at the plane of the array we can transform the integration over the solid angle to an integration over the array element coordinates to find
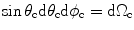 is just a differential solid angle as measured in these spherical coordinates. If we let
is just a differential solid angle as measured in these spherical coordinates. If we let 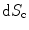 be a differential area element at the plane of the array we can transform the integration over the solid angle to an integration over the array element coordinates to find
be a differential area element at the plane of the array we can transform the integration over the solid angle to an integration over the array element coordinates to find![$$ {I}_{R}(\mathbf{y})=\frac{1}{2{{\text{ }\!\!\pi\!\!\text{ }}^{3}}{{\rho }_{2}}c_{\beta 2}^{4}}\int{\int{\frac{{{\omega }^{2}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{c}}},\omega)}{{{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{y},\omega) ]}^{2}}}\exp [{-}2\text{i}\omega {T}( {{\mathbf{x}}_{\text{c}}},\mathbf{y} ) ]}}\frac{\text{d}{{\Omega }_{\text{c}}}}{d{{S}_{\text{c}}}}\text{d}{{S}_{\text{c}}}\text{d}\omega . $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ21.gif)
(13.21)
The ratio 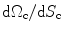 (see Fig. 13.2a, b) is easy to calculate for an array radiating into a single medium. We find
(see Fig. 13.2a, b) is easy to calculate for an array radiating into a single medium. We find 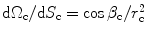 , where
, where 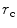 is the distance from the point
is the distance from the point 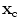 on the plane of the array to an image point
on the plane of the array to an image point 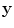 and
and 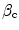 is the angle that the ray from
is the angle that the ray from 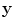 to
to 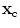 makes with respect to the normal to the plane of the array (Figs. 13.1 and 13.2b). For other more complex situations, such as the radiation of the array through a planar interface, as shown in Fig. 13.1, one can use ray tracing to calculate
makes with respect to the normal to the plane of the array (Figs. 13.1 and 13.2b). For other more complex situations, such as the radiation of the array through a planar interface, as shown in Fig. 13.1, one can use ray tracing to calculate 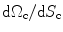 (see Appendix B for details) .
(see Appendix B for details) .
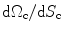 (see Fig. 13.2a, b) is easy to calculate for an array radiating into a single medium. We find
(see Fig. 13.2a, b) is easy to calculate for an array radiating into a single medium. We find 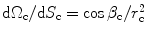 , where
, where 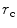 is the distance from the point
is the distance from the point 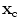 on the plane of the array to an image point
on the plane of the array to an image point 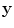 and
and 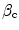 is the angle that the ray from
is the angle that the ray from  to
to  makes with respect to the normal to the plane of the array (Figs. 13.1 and 13.2b). For other more complex situations, such as the radiation of the array through a planar interface, as shown in Fig. 13.1, one can use ray tracing to calculate
makes with respect to the normal to the plane of the array (Figs. 13.1 and 13.2b). For other more complex situations, such as the radiation of the array through a planar interface, as shown in Fig. 13.1, one can use ray tracing to calculate  (see Appendix B for details) .
(see Appendix B for details) .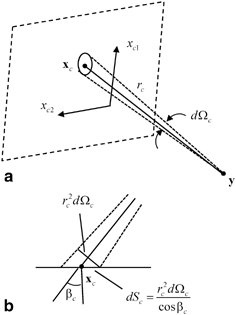
Fig. 13.2
a Geometry for relating the solid angle coordinates to Cartesian coordinates on the face of the array, and b a side view, showing the angle of the array with the face of the array
Equation (13.21) is essentially an imaging measurement model for forming an image of the reflectivity of a flaw from either immersion or contact pulse-echo measurements of the voltages 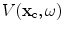 received from a flaw over all locations in the plane of the array and at all frequencies. In practice, of course, if one only has the voltages measured at the discrete locations of the array elements
received from a flaw over all locations in the plane of the array and at all frequencies. In practice, of course, if one only has the voltages measured at the discrete locations of the array elements 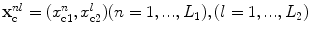 and at a finite set of positive frequencies,
and at a finite set of positive frequencies, 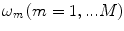 , we can only obtain a band-limited and aperture-limited image,
, we can only obtain a band-limited and aperture-limited image, 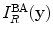 , given by
, given by
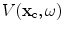 received from a flaw over all locations in the plane of the array and at all frequencies. In practice, of course, if one only has the voltages measured at the discrete locations of the array elements
received from a flaw over all locations in the plane of the array and at all frequencies. In practice, of course, if one only has the voltages measured at the discrete locations of the array elements 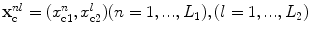 and at a finite set of positive frequencies,
and at a finite set of positive frequencies, 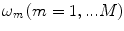 , we can only obtain a band-limited and aperture-limited image,
, we can only obtain a band-limited and aperture-limited image, 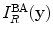 , given by
, given by![$$ {I}_{R}^{\text{BA}}(\mathbf{y})=\frac{\Delta {{x}_{\text{c}1}}\Delta {{x}_{\text{c}2}}\Delta \omega }{2{{\pi }^{3}}{{\rho }_{2}}c_{\beta 2}^{4}}2\operatorname{Re}\left\{ \sum\limits_{m=1}^{M}{\sum\limits_{n=1}^{{{L}_{1}}}{\sum\limits_{l=1}^{{{L}_{2}}}{\frac{\omega _{m}^{2}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( \mathbf{x}_{\text{c}}^{nl},{{\omega }_{m}} )}{{{[ \tilde{V}_{\beta }^{(1)}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} ) ]}^{2}}}}}}\exp [{-}2\text{i}{{\omega }_{m}}{T}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y} ) ]\frac{\text{d}{{\Omega }_{\text{c}}}}{\text{d}{{S}_{\text{c}}}}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y} ) \right\}, $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ22.gif)
(13.22)
where 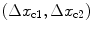 is the spacing between elements in the
is the spacing between elements in the 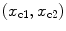 directions, respectively, and
directions, respectively, and 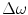 is the spacing between sampled frequencies in rad/s. The term
is the spacing between sampled frequencies in rad/s. The term 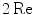 indicates twice the “real part” and is present because we are only summing over positive frequencies to generate the image of the flaw reflectivity. As discussed in Chap. 12, the measured voltages here are being divided (deconvolved) with a system function and an incident beam wave field term so that we must stabilize that deconvolution process to make it well behaved. Consider, for example, the immersion case where
indicates twice the “real part” and is present because we are only summing over positive frequencies to generate the image of the flaw reflectivity. As discussed in Chap. 12, the measured voltages here are being divided (deconvolved) with a system function and an incident beam wave field term so that we must stabilize that deconvolution process to make it well behaved. Consider, for example, the immersion case where 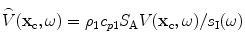 (see Eq. (11.37) with
(see Eq. (11.37) with 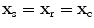 ). Then
). Then
 is the spacing between elements in the
is the spacing between elements in the 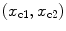 directions, respectively, and
directions, respectively, and 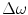 is the spacing between sampled frequencies in rad/s. The term
is the spacing between sampled frequencies in rad/s. The term 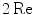 indicates twice the “real part” and is present because we are only summing over positive frequencies to generate the image of the flaw reflectivity. As discussed in Chap. 12, the measured voltages here are being divided (deconvolved) with a system function and an incident beam wave field term so that we must stabilize that deconvolution process to make it well behaved. Consider, for example, the immersion case where
indicates twice the “real part” and is present because we are only summing over positive frequencies to generate the image of the flaw reflectivity. As discussed in Chap. 12, the measured voltages here are being divided (deconvolved) with a system function and an incident beam wave field term so that we must stabilize that deconvolution process to make it well behaved. Consider, for example, the immersion case where 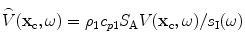 (see Eq. (11.37) with
(see Eq. (11.37) with 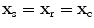 ). Then
). Then![$$ {I}^{\text{BA}}(\mathbf{y})=\frac{\Delta {{x}_{\text{c}1}}\Delta {{x}_{\text{c}2}}\Delta \omega }{2{{\pi }^{3}}{{\rho }_{2}}c_{\beta 2}^{4}}2\operatorname{Re}\left\{ \sum\limits_{m=1}^{M}{\sum\limits_{n=1}^{{{L}_{1}}}{\sum\limits_{l=1}^{{{L}_{2}}}{\frac{{{\rho }_{1}}{{c}_{p1}}{{S}_{\text{A}}}\omega _{m}^{2}V( \mathbf{x}_{\text{c}}^{nl},{{\omega }_{m}} )}{{{s}_{\text{I}}}( {{\omega }_{m}} ){{[ \tilde{V}_{\beta }^{(1)}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} ) ]}^{2}}}}}} \right. \left. .\exp [{-}2\text{i}{{\omega }_{m}}{T}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y} ) ]\frac{\text{d}{{\Omega }_{\text{c}}}}{\text{d}{{S}_{\text{c}}}}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y} ) \right\}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ23.gif)
(13.23)
In implementing Eq. (13.23) we can replace the deconvolution by division again with a Wiener filter , i.e.
![$$ \frac{V( \mathbf{x}_{\text{c}}^{nl},{{\omega }_{m}} )}{{{s}_{\text{I}}}( {{\omega }_{m}} ){{[ \tilde{V}_{\beta }^{(1)}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} ) ]}^{2}}}\to {{V}_{\text{W}}}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} ), $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ24.gif)
(13.24)
where the filtered voltage is
![$$ {{V}_{\text{W}}}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} )=\frac{V( \mathbf{x}_{\text{c}}^{nl},{{\omega }_{m}} ){{\left\{ {{s}_{\text{I}}}( {{\omega }_{m}} ){{[ \tilde{V}_{\beta }^{(1)}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} ) ]}^{2}} \right\}}^{*}}}{{{\left| {{s}_{\text{I}}}( {{\omega }_{m}} ){{[ \tilde{V}_{\beta }^{(1)}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} ) ]}^{2}} \right|}^{2}}{{\varepsilon }^{2}}\max \left\{ {{\left| {{s}_{\text{I}}}( {{\omega }_{m}} ){{[ \tilde{V}_{\beta }^{(1)}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} ) ]}^{2}} \right|}^{2}} \right\}} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ25.gif)
(13.25)
so that in the immersion case we would find
![$$ {I}^{\text{BA}}(\mathbf{y})=\frac{\Delta {{x}_{\text{c}1}}\Delta {{x}_{\text{c}2}}\Delta \omega }{2{{\pi }^{3}}{{\rho }_{2}}c_{\beta 2}^{4}}2\operatorname{Re}\left\{ \sum\limits_{m=1}^{M}{\sum\limits_{n=1}^{{{L}_{1}}}{\sum\limits_{l=1}^{{{L}_{2}}}{{{\rho }_{1}}{{c}_{p1}}{{S}_{\text{A}}}\omega _{m}^{2}{{V}_{\text{W}}}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y},{{\omega }_{m}} )}}} \right. \left. .\exp [{-}2\text{i}{{\omega }_{m}}{T}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y} ) ]\frac{\text{d}{{\Omega }_{\text{c}}}}{\text{d}{{S}_{\text{c}}}}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y} ) \right\}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ26.gif)
(13.26)
This 3-D imaging measurement model can also be related to a corresponding SAFT algorithm, as done in Chap. 12 for the simpler 2-D problems. If we set 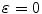 in the Wiener filter and simply ignore all the terms in Eq. (13.26) except the constant
in the Wiener filter and simply ignore all the terms in Eq. (13.26) except the constant 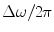 , the measured voltages, and the phase terms involving the propagation terms
, the measured voltages, and the phase terms involving the propagation terms 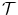 we find the SAFT image (see Eq. (12.5)) :
we find the SAFT image (see Eq. (12.5)) :
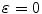 in the Wiener filter and simply ignore all the terms in Eq. (13.26) except the constant
in the Wiener filter and simply ignore all the terms in Eq. (13.26) except the constant 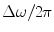 , the measured voltages, and the phase terms involving the propagation terms
, the measured voltages, and the phase terms involving the propagation terms 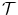 we find the SAFT image (see Eq. (12.5)) :
we find the SAFT image (see Eq. (12.5)) :![$$ {I}_{\text{SAFT}}(\mathbf{y})=2\operatorname{Re}\left\{ \frac{\Delta \omega }{2\pi }\sum\limits_{m=1}^{M}{\sum\limits_{n=1}^{{{L}_{1}}}{\sum\limits_{l=1}^{{{L}_{2}}}{V( \mathbf{x}_{\text{c}}^{nl},{{\omega }_{m}} )\exp [{-}2\text{i}{{\omega }_{m}}{T}( \mathbf{x}_{\text{c}}^{nl},\mathbf{y} ) ]}}} \right\}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ27.gif)
(13.27)
The imaging measurement model of Eq. (13.21) is applicable to the imaging of large or small surfaces. When the flaw is small enough so that the incident wave fields do not vary significantly over the flaw surface we have
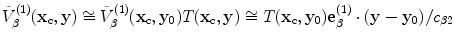
(13.28)
for a fixed image point 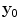 near the flaw surface and Eq. (13.21) becomes
near the flaw surface and Eq. (13.21) becomes
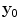 near the flaw surface and Eq. (13.21) becomes
near the flaw surface and Eq. (13.21) becomes![$${I}_{R}(\mathbf{y})=\frac{1}{2{{\text{ }\!\!\pi\!\!\text{ }}^{3}}{{\rho }_{2}}c_{\beta 2}^{4}}\int{\int{\left\{ \frac{{{\omega }^{2}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}\left( {{\mathbf{x}}_{\text{c}}},\omega \right)}{{{[\tilde{V}_{\beta }^{(1)}\left( {{\mathbf{x}}_{\text{c}}},{{\mathbf{y}}_{0}},\omega \right)\exp \left\{ \text{i}\omega {T}\left( {{\mathbf{x}}_{\text{c}}},{{\mathbf{y}}_{0}} \right) \right\}]}^{2}}} \right.}} \quad\left. .\exp \left[ -2\text{i}{{k}_{\beta 2}}\mathbf{e}_{\beta }^{(1)}\cdot \left( \mathbf{y}-{{\mathbf{y}}_{0}} \right) \right]\frac{\text{d}{{\Omega }_{\text{c}}}}{\text{d}{{S}_{\text{c}}}}\text{d}{{S}_{\text{c}}}\text{d}\omega \right\},$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ29.gif)
(13.29)
which is a POFFIS-style imaging expression, similar to the 2-D case considered in Chap. 12. Computationally, Eq. (13.29) requires much less effort than Eq. (13.21) to implement since one needs to calculate the incident wave field terms only for the one fixed point 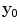 for all image points
for all image points 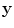 . However, in implementing Eq. (13.29) one should only use images points near the flaw surface so that Eq. (13.28) is not violated. Thus, with multiple flaws that are widely separated one should locally image each flaw individually with Eq. (13.29).
. However, in implementing Eq. (13.29) one should only use images points near the flaw surface so that Eq. (13.28) is not violated. Thus, with multiple flaws that are widely separated one should locally image each flaw individually with Eq. (13.29).
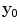 for all image points
for all image points 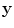 . However, in implementing Eq. (13.29) one should only use images points near the flaw surface so that Eq. (13.28) is not violated. Thus, with multiple flaws that are widely separated one should locally image each flaw individually with Eq. (13.29).
. However, in implementing Eq. (13.29) one should only use images points near the flaw surface so that Eq. (13.28) is not violated. Thus, with multiple flaws that are widely separated one should locally image each flaw individually with Eq. (13.29).As done in Chap. 12 for the 2-D scalar case, we can write Eq. (13.29) in terms of the far field scattering amplitude of the flaw by using the Thompson-Gray measurement model (Eqs. (11.26) and (11.30)) for either an immersion or contact setup. In the pulse-echo case we have 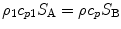 , and
, and 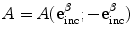 , so that we find that for both the immersion and contact cases
, so that we find that for both the immersion and contact cases
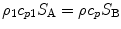 , and
, and 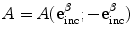 , so that we find that for both the immersion and contact cases
, so that we find that for both the immersion and contact cases![$$ {I}_{R}(\mathbf{y})=\frac{2}{{{\text{ }\!\!\pi\!\!\text{ }}^{2}}{{c}_{\beta 2}}}\int{\int{\text{i}{{k}_{\beta 2}}A( \mathbf{e}_{\text{inc}}^{\beta };-\mathbf{e}_{\text{inc}}^{\beta } )\exp [{-}2\text{i}\omega \mathbf{e}_{\beta }^{(1)}\cdot ( \mathbf{y}-{{\mathbf{y}}_{0}} ) ]\frac{\text{d}{{\Omega }_{\text{c}}}}{\text{d}{{S}_{\text{c}}}}\text{d}{{S}_{\text{c}}}\text{d}\omega .}} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ30.gif)
(13.30)
Equation (13.30) can be used to simulate POFFIS-style images generated by an imaging measurement model for a flaw whose far field scattering amplitude can be modeled by semi-analytical or numerical means. When discussing POFFIS imaging, Bleistein [3] obtained this result for 3-D scalar wave problems (see Eq. 9.2.9 in [3]), a result which we see here is also directly applicable to imaging with elastic waves .
We can also develop an imaging measurement model for the pulse-echo edge response of cracks following similar steps to those used in Chap. 12 for the scalar 2-D case. We will again assume that there is no specular response from the crack surface (which will be assumed to be entirely lit by the incident waves) so that we must start by modifying Eq. (13.2) to reflect that fact. In Chap. 11, we obtained this form of an approximate measurement model by using the Kirchhoff approximation to obtain (see Eq. (11.47), written here in terms of velocities)
![$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}({{\mathbf{x}}_{\text{c}}},\omega )=-\int_{S}{\left\{ I(\mathbf{x}){{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{x},\omega) ]}^{2}}\exp [ \text{i}\omega \phi ( {{\mathbf{x}}_{\text{c}}},\mathbf{x} ) ]\text{d}S(\mathbf{x}) \right\}}, $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ31.gif)
(13.31)
where 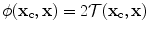 .The integrand term
.The integrand term 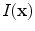 was evaluated at the stationary phase points on the flaw surface to model the specular response of the surface. Here, instead we keep the original integral term, Eq. (11.48), which for pulse-echo, same mode responses reduces to
was evaluated at the stationary phase points on the flaw surface to model the specular response of the surface. Here, instead we keep the original integral term, Eq. (11.48), which for pulse-echo, same mode responses reduces to
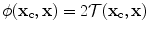 .The integrand term
.The integrand term 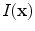 was evaluated at the stationary phase points on the flaw surface to model the specular response of the surface. Here, instead we keep the original integral term, Eq. (11.48), which for pulse-echo, same mode responses reduces to
was evaluated at the stationary phase points on the flaw surface to model the specular response of the surface. Here, instead we keep the original integral term, Eq. (11.48), which for pulse-echo, same mode responses reduces to![$$ I(\mathbf{x})={{n}_{j}}{{C}_{ijkl}}\left[ \sum\limits_{m=p,sv}{\left( \frac{R_{23}^{m;\beta }d_{\beta i}^{(2)}d_{mk}^{r}e_{ml}^{r}}{{{c}_{m2}}}-\frac{R_{23}^{m;\beta }d_{\beta k}^{(2)}d_{mi}^{r}e_{\beta l}^{(2)}}{{{c}_{\beta 2}}} \right)} \right]. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ32.gif)
(13.32)
Now, let us define a vector field, 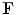 , as
, as
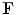 , as
, as![$$ \mathbf{F}=-\frac{1}{\text{i}\omega }\frac{\mathbf{n}\times \nabla \phi }{|\nabla \phi {{|}^{2}}-{{(\nabla \phi \cdot \mathbf{n})}^{2}}}I(\mathbf{x}){{[ \tilde{V}_{\beta }^{(1)} ]}^{2}}\exp [\text{i}\omega \phi ], $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ33.gif)
(13.33)
which is possible since if there are no specular points on the crack surface the denominator in Eq. (13.33) never vanishes. At high frequencies the derivatives of this field come from derivatives of the phase term so that we have, approximately
![$$ \mathbf{n}\cdot (\nabla \times \mathbf{F})=-I(\mathbf{x}){{[ \tilde{V}_{\beta }^{(1)} ]}^{2}}\exp [\text{i}\omega \phi ] $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ34.gif)
(13.34)
where we have used the vector identity
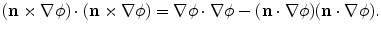
(13.35)
Thus, using Stokes theorem
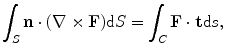
(13.36)
![$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}({{\mathbf{x}}_{\text{c}}},\omega )=-\frac{1}{\text{i}\omega }\int_{C}{\frac{(\mathbf{n}\times \nabla \phi )\cdot \mathbf{t}}{|\nabla \phi {{|}^{2}}-{{(\nabla \phi \cdot \mathbf{n})}^{2}}}I(\mathbf{x}){{\left[ \tilde{V}_{\beta }^{(1)} \right]}^{2}}\exp \text{ }\!\![\!\!\text{ i}\omega \phi ]\text{d}s}.$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ37.gif)
(13.37)
If we introduce the singular function of the crack edge, 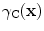 , where for any function
, where for any function 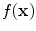
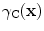 , where for any function
, where for any function 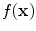
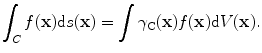
(13.38)
Equation (13.37) can be rewritten in a form very similar to Eq. (13.4), namely
![$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{c}}},\omega)=\tfrac{2{{\rho }_{2}}c_{\beta 2}^{2}}{\text{i}\omega }\int{\left\{ {{\mathcal{R}}_{\text{e}}}{{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{x},\omega) ]}^{2}}\exp [ 2\text{i}\omega \mathcal{T}( {{\mathbf{x}}_{\text{c}}},\mathbf{x} ) ]\text{d}V(\mathbf{x}) \right\},} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ39.gif)
(13.39)
where the reflectivity of the crack edge, 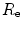 , is defined here as
, is defined here as
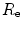 , is defined here as
, is defined here as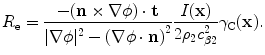
(13.40)
As discussed in Chap. 12 for the 2-D case, we cannot expect to image explicitly this reflectivity at each point on the edge because of the dependence of the coefficients of 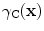 in Eq. (13.40) on the incident and scattering directions, but we can ignore those dependencies and write
in Eq. (13.40) on the incident and scattering directions, but we can ignore those dependencies and write 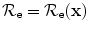 only in trying to image the crack edge singularities. In that case Eqs. (13.39) and (13.4) are nearly identical. In fact, we can make the forms identical by making the replacement
only in trying to image the crack edge singularities. In that case Eqs. (13.39) and (13.4) are nearly identical. In fact, we can make the forms identical by making the replacement 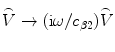 in Eq. (13.4). Thus, making the same replacement in the imaging measurement model of Eq. (13.21), we obtain for an image of the crack edge
in Eq. (13.4). Thus, making the same replacement in the imaging measurement model of Eq. (13.21), we obtain for an image of the crack edge
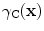 in Eq. (13.40) on the incident and scattering directions, but we can ignore those dependencies and write
in Eq. (13.40) on the incident and scattering directions, but we can ignore those dependencies and write 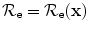 only in trying to image the crack edge singularities. In that case Eqs. (13.39) and (13.4) are nearly identical. In fact, we can make the forms identical by making the replacement
only in trying to image the crack edge singularities. In that case Eqs. (13.39) and (13.4) are nearly identical. In fact, we can make the forms identical by making the replacement 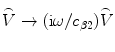 in Eq. (13.4). Thus, making the same replacement in the imaging measurement model of Eq. (13.21), we obtain for an image of the crack edge
in Eq. (13.4). Thus, making the same replacement in the imaging measurement model of Eq. (13.21), we obtain for an image of the crack edge![$$ {I}_{\text{e}}(\mathbf{y})=\frac{1}{2{{\text{ }\!\!\pi\!\!\text{ }}^{3}}c_{\beta 2}^{4}}\int{\int{\frac{( \text{i}\omega /{{c}_{\beta 2}} ){{\omega }^{2}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{c}}},\omega)}{{{[ \tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{c}}},\mathbf{y},\omega) ]}^{2}}}\exp [{-}2\text{i}\omega {T}( {{\mathbf{x}}_{\text{c}}},\mathbf{y} ) ]\frac{\text{d}{{\Omega }_{\text{c}}}}{\text{d}{{S}_{\text{c}}}}\text{d}{{S}_{\text{c}}}\text{d}\omega ,}} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ41.gif)
(13.41)
with 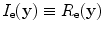 . As found in Chap. 12 for the 2-D scalar case, we see that a 3-D crack image involves an additional
. As found in Chap. 12 for the 2-D scalar case, we see that a 3-D crack image involves an additional 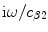 factor not present in the image of the specular surface response. Although we have only considered the pulse-echo case here, following the same steps for the full matrix imaging approach described in the next section also leads to a crack edge image that is related to the specular flaw response by making the replacement
factor not present in the image of the specular surface response. Although we have only considered the pulse-echo case here, following the same steps for the full matrix imaging approach described in the next section also leads to a crack edge image that is related to the specular flaw response by making the replacement 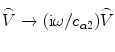 .
.
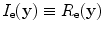 . As found in Chap. 12 for the 2-D scalar case, we see that a 3-D crack image involves an additional
. As found in Chap. 12 for the 2-D scalar case, we see that a 3-D crack image involves an additional 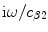 factor not present in the image of the specular surface response. Although we have only considered the pulse-echo case here, following the same steps for the full matrix imaging approach described in the next section also leads to a crack edge image that is related to the specular flaw response by making the replacement
factor not present in the image of the specular surface response. Although we have only considered the pulse-echo case here, following the same steps for the full matrix imaging approach described in the next section also leads to a crack edge image that is related to the specular flaw response by making the replacement 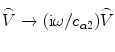 .
.13.2 Full Matrix Imaging
The previous section showed that measuring all the pulse-echo responses from an array of elements in a 2-D array was sufficient to generate a 3-D image of a flaw . If instead, one captures all combinations of responses from element pairs (full-matrix capture) then one can also form up an image. The element pairs can be on the same array or on separate arrays, as shown in Fig. 13.3. As done in Chap. 12 for the scalar problem, we will first consider the case where we have a single sending element and receive with all elements of the receiving array. Again, we will consider the parameters 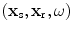 as continuous variables. From Eq. (11.62) we had
as continuous variables. From Eq. (11.62) we had
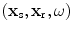 as continuous variables. From Eq. (11.62) we had
as continuous variables. From Eq. (11.62) we had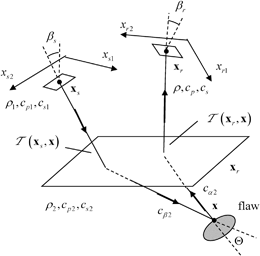
Fig. 13.3
A pitch-catch setup where separate array elements are used as senders and receivers
![$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega)=-2{{\rho }_{2}}{{c}_{\alpha 2}}{{\omega }^{2}}\int_{{{S}_{\text{lit}}}}{\left\{ R_{23}^{\alpha ;\beta }( e_{\alpha k}^{r}{{n}_{k}} )\tilde{U}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{s}}},\mathbf{x},\omega)\tilde{U}_{\alpha }^{(2)}( {{\mathbf{x}}_{\text{r}}},\mathbf{x},\omega)\exp [ \text{i}\omega \phi ( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega) ]\text{d}S(\mathbf{x}) \right\},} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ42.gif)
(13.42)
which, in terms of the velocities 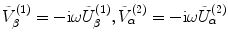 becomes
becomes
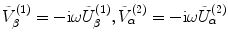 becomes
becomes![$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega)=2{{\rho }_{2}}{{c}_{\alpha 2}}\int_{{{S}_{\text{lit}}}}{\left\{ R_{23}^{\alpha ;\beta }( e_{\alpha k}^{r}{{n}_{k}} )\tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{s}},\mathbf{x},\omega)\tilde{V}_{\alpha }^{(2)}( {{\mathbf{x}}_{\text{r}}},\mathbf{x},\omega)\exp [ \text{i}\omega \phi ( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega) ]\text{d}S(\mathbf{x}) \right\}}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ43.gif)
(13.43)
Introducing the singular function of the surface again we can write Eq. (13.43) as
![$$\overset{\frown }{\mathop{V}}\,\left( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega \right)=2{{\rho }_{2}}{{c}_{\alpha 2}}\int{\{}R_{23}^{\alpha ;\beta }\left( e_{\alpha k}^{r}{{n}_{k}} \right){{\gamma }_{\text{S}}}(\mathbf{x})\tilde{V}_{\beta }^{(1)}\left( {{\mathbf{x}}_{\text{s}}},\mathbf{x},\omega \right)\tilde{V}_{\alpha }^{(2)}\left( {{\mathbf{x}}_{\text{r}}},\mathbf{x},\omega \right)\quad .\exp \left[ \text{i}\omega \phi \left( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\mathbf{x} \right)
\right]\text{d}V(\mathbf{x})\}.$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ44.gif)
(13.44)
We will parameterize the receiving array element locations, 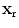 , assumed here to lie on a planar surface, in terms of two auxiliary variables
, assumed here to lie on a planar surface, in terms of two auxiliary variables 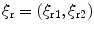 , i.e.
, i.e. 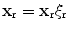 , and in this case define the flaw image as
, and in this case define the flaw image as
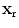 , assumed here to lie on a planar surface, in terms of two auxiliary variables
, assumed here to lie on a planar surface, in terms of two auxiliary variables 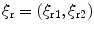 , i.e.
, i.e. 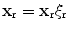 , and in this case define the flaw image as
, and in this case define the flaw image as 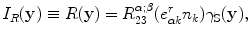
(13.45)
which reduces to our previous definition, Eq. (13.5), for the pulse-echo case. Since Eq. (13.44) is again a Fourier-like integral we will attempt to invert that equation and form an image via the relation
![$$ {I}_{R}(\mathbf{y})=\int{\int{K( \mathbf{y},{{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}( {{\xi }_{\text{r}}} ),\omega)\cdot \exp [{-}\text{i}\omega \phi ( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}( {{\xi }_{\text{r}}} ),\omega) ]{{\text{d}}^{2}}{{\xi }_{\text{r}}}\text{d}\omega }}. $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ46.gif)
(13.46)
Placing Eq. (13.44) into (13.46) gives formally
![$$ {I}_{R}(\mathbf{y})=\int{\int{\int{K( \mathbf{y},{{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega)\left\{ 2{{\rho }_{2}}{{c}_{\alpha 2}}{I}_{R}(\mathbf{x})\tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{s}}},\mathbf{x},\omega)\tilde{V}_{\alpha }^{(2)}( {{\mathbf{x}}_{\text{r}}},\mathbf{x},\omega)\exp [ \text{i}\omega \phi ( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\mathbf{x} )-\text{i}\omega \phi ( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}( {{\xi }_{\text{r}}} ),\mathbf{y} ) ] \right\}{{\text{d}}^{2}}{{\xi }_{\text{r}}}\text{d}\omega \text{d}V(\mathbf{x})}}} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ47.gif)
(13.47)
As in the pulse-echo case Eq. (13.47) can be true if in some sense we have
![$$ \delta (\mathbf{x}-\mathbf{y})=\int{\int{K( \mathbf{y},{{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega)}}\left\{ 2{{\rho }_{2}}{{c}_{\alpha 2}}\tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{s}}},\mathbf{x},\omega)\tilde{V}_{\alpha }^{(2)}( {{\mathbf{x}}_{\text{r}}},\mathbf{x},\omega)\exp [ \text{i}\omega \phi ( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\mathbf{x} )-\text{i}\omega \phi ( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}( {{\xi }_{\text{r}}} ),\mathbf{y} ) ] \right\}{{\text{d}}^{2}}{{\xi }_{\text{r}}}\text{d}\omega . $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ48.gif)
(13.48)
This is possible since at high frequencies again we expect the major contribution to come from this highly oscillatory integrand around the critical point 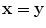 . Evaluating the amplitude of the integrand of the integral at that critical point and expanding the phase to first order, i.e .
. Evaluating the amplitude of the integrand of the integral at that critical point and expanding the phase to first order, i.e .
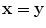 . Evaluating the amplitude of the integrand of the integral at that critical point and expanding the phase to first order, i.e .
. Evaluating the amplitude of the integrand of the integral at that critical point and expanding the phase to first order, i.e .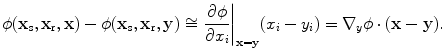
(13.49)
Equation (13.48) becomes
![$$ \delta (\mathbf{x}-\mathbf{y})=\int{\int{K( \mathbf{y},{{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega)\left\{ 2{{\rho }_{2}}{{c}_{\alpha 2}}\tilde{V}_{\beta }^{(1)}( {{\mathbf{x}}_{\text{s}}},\mathbf{y},\omega)\tilde{V}_{\alpha }^{(2)}( {{\mathbf{x}}_{\text{r}}},\mathbf{y},\omega)\exp [ \text{i}\omega {{\nabla }_{y}}\phi \cdot (\mathbf{x}-\mathbf{y}) ] \right\}{{\text{d}}^{2}}{{\xi }_{\text{r}}}\text{d}\omega .}} $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ50.gif)
(13.50)
Now, defining a wave vector, 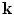 , as
, as
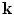 , as
, as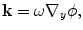
(13.51)
we transform the integral in Eq. (13.50) to one over 3-D k-space:
![$$ {\text{}} \delta (\mathbf{x}-\mathbf{y})=\int{\int{K(\mathbf{y},{{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}},\omega)}}\left\{2{{\rho }_{2}}{{c}_{\alpha 2}}\tilde{V}_{\beta }^{(1)}({{\mathbf{x}}_{\text{s}}},\mathbf{y},\omega)\tilde{V}_{\alpha}^{(2)}( {{\mathbf{x}}_{\text{r}}},\mathbf{y},\omega) \right. \\ \quad\left. \left| \frac{\partial (\omega ,{{\xi }_{\text{r}1}},{{\xi}_{\text{r}2}})}{\partial (\mathbf{k})} \right|\exp \text{ }\!\![\!\!\text{ i}\mathbf{k}\cdot (\mathbf{x}-\mathbf{y})]\right\}{{\text{d}}^{3}}\mathbf{k}, $$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ52.gif)
(13.52)
where the inverse of the Jacobian of the transformation can be written as
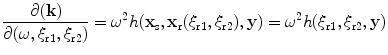
(13.53)
in terms of the Beylkin determinant , 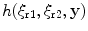 . Thus, if one takes the function
. Thus, if one takes the function 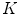 as
as
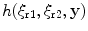 . Thus, if one takes the function
. Thus, if one takes the function 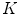 as
as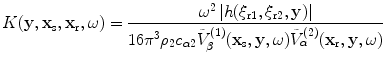
(13.54)
one obtains the k-space transform representation of the delta function again (see Eqs. (3.17)) and Eq. (13.46) becomes
![$${{I}_{R}}(\mathbf{y})=\frac{1}{16\text{ }\pi {{}^{3}}{{\rho }_{2}}{{c}_{\alpha 2}}}\int{\int{\frac{{{\omega }^{2}}\left| h({{\xi }_{\text{r}1}},{{\xi }_{\text{r}2}},\mathbf{y}) \right|\overset{\frown }{\mathop{V}}\,({{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}({{\xi }_{\text{r}}}),\omega )}{\tilde{V}_{\beta }^{(1)}({{\mathbf{x}}_{\text{s}}},\mathbf{y},\omega )\tilde{V}_{\alpha }^{(2)}({{\mathbf{x}}_{\text{r}}}({{\xi }_{\text{r}}}),\mathbf{y},\omega )}}}\cdot \exp [-\text{i}\omega \phi ({{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}({{\xi }_{\text{r}}}),\mathbf{y})]{{\text{d}}^{2}}{{\xi }_{\text{r}}}\text{d}\omega
.$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ55.gif)
(13.55)
If one chooses the parameters 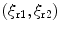 to be spherical coordinates
to be spherical coordinates 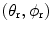 at the image point
at the image point  , as shown in Appendix A the magnitude of this Beylkin determinant simply becomes
, as shown in Appendix A the magnitude of this Beylkin determinant simply becomes
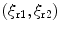 to be spherical coordinates
to be spherical coordinates 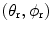 at the image point
at the image point  , as shown in Appendix A the magnitude of this Beylkin determinant simply becomes
, as shown in Appendix A the magnitude of this Beylkin determinant simply becomes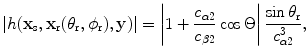
(13.56)
where 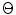 is the angle at
is the angle at 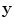 between a ray path from the source to that point and a ray path from the receiver to that point (see Fig. 13.3). Then Eq. (13.55) is
between a ray path from the source to that point and a ray path from the receiver to that point (see Fig. 13.3). Then Eq. (13.55) is
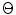 is the angle at
is the angle at 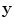 between a ray path from the source to that point and a ray path from the receiver to that point (see Fig. 13.3). Then Eq. (13.55) is
between a ray path from the source to that point and a ray path from the receiver to that point (see Fig. 13.3). Then Eq. (13.55) is![$${{I}_{R}}(\mathbf{y})=\frac{1}{16\text{ }\pi {{\text{ }}^{3}}{{\rho }_{2}}c_{\alpha 2}^{4}}\int{\int{\left| 1+\frac{{{c}_{\alpha 2}}}{{{c}_{\beta 2}}}\cos \Theta \right|\frac{{{\omega }^{2}}\overset{\frown }{\mathop{V}}\,\left( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}\left( {{\xi }_{\text{r}}} \right),\omega \right)}{\tilde{V}_{\beta }^{(1)}\left( {{\mathbf{x}}_{\text{s}}},\mathbf{y},\omega \right)\tilde{V}_{\alpha }^{(2)}\left( {{\mathbf{x}}_{\text{r}}}\left( {{\xi }_{\text{r}}} \right),\mathbf{y},\omega \right)}}}\quad \exp \left[ -\text{i}\omega \phi \left( {{\mathbf{x}}_{\text{s}}},{{\mathbf{x}}_{\text{r}}}\left( {{\xi }_{\text{r}}} \right),\mathbf{y} \right) \right]\text{d}{{\Omega }_{\text{r}}}\text{d}\omega,$$](/wp-content/uploads/2016/05/A314073_1_En_13_Chapter_Equ57.gif)
(13.57)
where 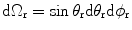 is a solid angle corresponding to different
is a solid angle corresponding to different 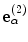 directions at
directions at 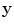 from the receivers. If we relate this solid angle to a corresponding area,
from the receivers. If we relate this solid angle to a corresponding area, 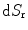 , on the plane of the receiving elements then we have
, on the plane of the receiving elements then we have
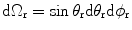 is a solid angle corresponding to different
is a solid angle corresponding to different 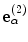 directions at
directions at 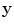 from the receivers. If we relate this solid angle to a corresponding area,
from the receivers. If we relate this solid angle to a corresponding area, 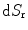 , on the plane of the receiving elements then we have
, on the plane of the receiving elements then we haveStay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree